Підготовка до ЗНО / НМТ: Ірраціональні вирази
1.8 Ірраціональні вирази
І. Числові множини
|
Числові множини |
|||
|
|
Назва |
Означення |
Приклади |
|
Натуральні (N) |
використовуютьcя при лічбі |
|
|
|
Цілі (Z) |
цілі від'ємні числа, цілі додатні числа |
|
|
|
Раціональні або дробові (Q) |
можна подати як частку двох цілих |
|
|
|
Ірраціональні (I) |
не можна подати як частку двох цілих |
|
|
|
Дійсні (R) |
всі можливі числа |
|
|

ІІ. Квадратний корінь
|
Властивості квадратного кореня |
||
|
|
|
|

ІІІ. Старші корені
|
Представлення кореня як степеня |
|
|
Будь-який корінь можна подати як степеневий вираз. Це дозволяє використовувати властивості степенів при роботі з коренями |
|
|
|
|

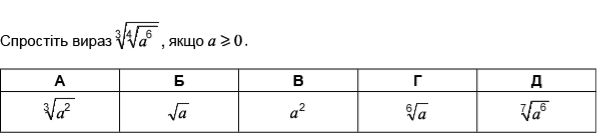
ІV. Порівняння степеневих виразів
|
Правило порівняння степеневих виразів |
|
Щоб порівняти два степеневі вирази, треба перетворити їх так, щоб в них були однакові основи або однакові степені |

V. Знищення ірраціональності
|
Знищення ірраціональності |
|||
|
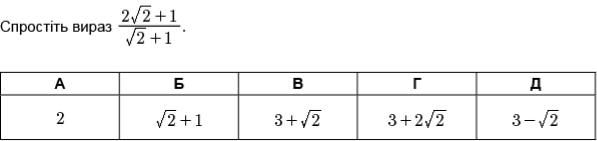
Ірраціональний дріб спрощується, якщо позбавитись від квадратних коренів у його знаменнику. Це можна зробити шляхом домноження і ділення дробу на спряжений вираз |
|||
|
Знаменник дробу |
|
|
|
|
Спряжений вираз |
|
|
|
|
Резюме |
|
Домашня робота


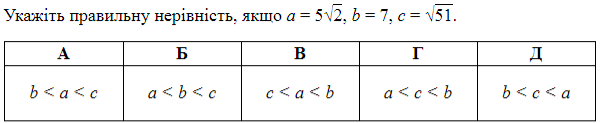
![]()
Використані джерела
- Завдання ЗНО / НМТ минулих років: zno.osvita.ua/mathematics
- Платформа для підготовки до ЗНО / НМТ: skywing.online


про публікацію авторської розробки
Додати розробку


