Підготовка до ЗНО з теми "Дійсні числа"
Підготовка до ЗНО
Тема: Дійсні числа
Множина-це сукупність об’єктів , як об’єднані в сукупність за певною ознакою (є спеціальні назви)
Множина є заданою, якщо є задана характеристика об’єктів множини.
ℕ - множина натуральних чисел,
ℤ - множина цілих чисел,
ℚ - множина раціональних чисел,
ℝ - множина дійсних чисел,
ℂ - множина комплексних чисел.
Кожний об’єкт, що входить до множини А, називається елементом цієї множини.
Зазвичай елементи позначають малими латинськими літерами: a, b, c, d тощо.
Умовні позначки.
![]() - знак належності для елементів множини
- знак належності для елементів множини![]() - знак неналежності для елементів множини
- знак неналежності для елементів множини![]() - знак включення для множин
- знак включення для множин![]() - знак об’єднання для множин
- знак об’єднання для множин![]() - знак перетину (перерізу) для множин
- знак перетину (перерізу) для множин![]() - порожня множина
- порожня множина
Якщо a належить множині A, то пишуть a ![]() A (читають: «a належить множині A»).
A (читають: «a належить множині A»).
Якщо b не належить множині A, то пишуть b ![]() A (читають: «b не належить множині A»).
A (читають: «b не належить множині A»).
Множина, що не містить жодного елемента, називається порожньою множиною і позначається ![]() .
.
Означення. Множина називається числовою, якщо її елементами являються числа.
Цифри – це знаки, якими позначають числа.
Цифр десять(0,1,2,3,4,5,6,7,8,9)
Які числа ви знаєте? З яких чисел почалося ваше знайомство з математикою? Коли ви прийшли до школи, ви вміли рахувати. Вивчили цифри від 0 до 9. А вже потім почалося знайомство з числами.
Всі числа можна віднести до тієї чи іншої групи, об’єднуючи їх за певними ознаками та властивостями. Найпростішою та найзрозумілішою множиною чисел є натуральні числа. Натуральні числа — це числа, які виникають природним чином при лiчбi предметів. Наприклад: 1,2,3,4…
Натуральні числа – це числа, які використовують під час лічби. Натуральних чисел безліч.
- Числа, якими ми рахуємо називаються натуральними.
Натуральні числа 1,2,3,… - це числа, що використовуються для рахування предметів або для вказування порядкового номера того чи іншого предмета серед однорідних предметів. Будь-яке натуральне число можна записати за допомогою десяти арабських цифр: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Числові множини прийнято позначати латинськими великими літерами. Множину натуральних чисел позначають знаком N.

Найменше натуральне число – 1. Найбільшого натурального числа не існує.
У III ст. до н. є. Архімед довів, що цей ряд чисел нескінченний. Множину натуральних чисел позначають літерою N. У цій множині введені дві дії: додавання та множення. Сума і добуток двох натуральних чисел є число натуральне. Наприклад, 5 + 6 =11, 2 ∙ 5 = 10 і т. п. Різниця натуральних чисел не завжди є натуральним числом. Наприклад, 3 - 10 не є натуральним числом.
3![]() N, 0
N, 0 ![]() N.
N.
Потім, поступово, під час вивчення математики до них додалися інші числа. Для того щоб можна було віднімати будь-які натуральні числа, вводяться число нуль та від'ємні числа.
В шостому класі, коли вивчали від’ємні числа, познайомились з поняттям протилежні числа. а і а: наприклад 2 і - 2 або 5 і – 5. Протилежні відрізняються знаком, і сума чисел дорівнює «0». Два числа, які відрізняються одне від одного лише знаками, називаються протилежними числами. Тільки одне число протилежне саме собі. Це число 0.
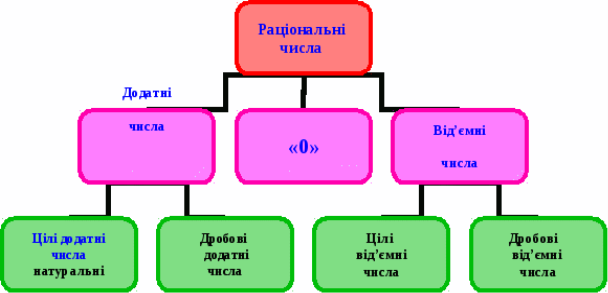
- Натуральні їм протилежні та «0» разом складають цілі числа.
Натуральні належать до множини додатних чисел. Протилежні тоді будуть їм від’ємними. «0» не належить ні до додатних, ні до від’ємних чисел.
Z - множина цілих чисел; ..., -3,-2, -1, 0, 1,2,3,4,5,6,7,... N ![]() Z .
Z .
Число нуль визначають як нейтральний елемент множини чисел. Це означає, що додавання цього числа до будь-яких інших чисел не змінює їх. Число нуль позначають 0. Отже,
а + 0 = а, де а — довільне число.
Цілим від'ємним числом - п, де п — натуральне число, називають таке число, для якого виконується тотожність:
(- п) + п = 0.
Число 0 не є натуральним числом.
Цілі числа можна зображати на прямій, узявши на ній за початок відліку точку О(0). Далі по обидва боки від точки О, якій відповідає 0, відкладають рівні відрізки, позначаючи їх кінці цифрами. Числа праворуч від 0 — додатні (зокрема, натуральні), ліворуч — від'ємні.
(також) 3![]() Z; 0
Z; 0![]() Z.
Z.
Таку пряму називають числовою прямою. Із двох чисел більшим вважається те, яке лежить далі праворуч на числовій прямій.
Множення та ділення двох чисел з однаковими знаками:
-a ∙(-b) = a ∙ b; - а : (-b) = a : b.
l) -3 ∙5 = - 15; 2) 63:(-7) = -9.
Додавання двох чисел з однаковими знаками:
-a + (-b) = -(a + b).
l) -3 ∙ (- 10) = 3 ∙ 10 = 30;
2) - 27 : (- 3) = 27 : 3 = 9.
Додавання двох чисел із різними знаками:
a>b=>-a + b= -(а - b); -а + b= b - а.
-5 + (-6) = -(5 + 6) = -11.
Віднімання двох чисел з однаковими знаками:
а>b => -а - (-b) = -(а - b); -a - (-b) =b - a.
1) -13 - (-8) = - (13 - 8) = -5; 2) -20 - (-45) = 45 - 20 = 25.
Віднімання двох чисел із різними знаками:
-а - b = -(а + b); a - (-b) = a + b.
1) -13 - 6 = -(13 + 6) = -19; 2) 40 - (-65) = 40 + 65 = 105.
Потім ви познайомились з дробами. Дроби бувають звичайні та десяткові. Звичайні діляться на правильні і не правильні.
Правильний дріб – де чисельник менше знаменника. Неправильний – чисельник більше або дорівнює знаменнику. Дроби бувають скоротні і не скоротні. Найчастіше ми працюємо з десятковими дробами. Вони також бувають від’ємними і додатними. Десяткові дроби – це дроби, які ми записуємо за допомогою коми.
N ![]() Z
Z ![]() Q.
Q.
Раціональні числа – це числа, які можна подати у вигляді відношення ![]() , де m – ціле число, а n – натуральне. Кожне раціональне число можна записати у вигляді скінченого або нескінченого дробу.
, де m – ціле число, а n – натуральне. Кожне раціональне число можна записати у вигляді скінченого або нескінченого дробу.
- Цілі числа та дробові разом складають раціональні числа.
Q – множина раціональних чисел.
Раціональні це ті числа, які ми можемо представити у вигляді дробу, де чисельник і знатник є цілими числами. Точніше знаменник не дорівнює «0».
Краще сказати знаменник є натуральним числом. Чиє натуральне число раціональним? Так, наприклад, двійку ми можемо представити як ![]() .
.
3 = ![]() =
= ![]()
![]() Q
Q
Всі натуральні числа, цілі числа є раціональними числами. Ми можемо сказати, що множина цілих чисел є підмножиною раціональних.
![]() , де m – ціле число,n – натуральне. Наприклад, 7=
, де m – ціле число,n – натуральне. Наприклад, 7=![]()
Раціональне число можна подати у вигляді скінченого десяткового дробу , як наприклад ![]() або нескінченого періодичного десяткового дробу, як
або нескінченого періодичного десяткового дробу, як ![]() , Цифра 3, яка повторюється є періодом дробу. 3=3,(0)..,4 =4,(0).
, Цифра 3, яка повторюється є періодом дробу. 3=3,(0)..,4 =4,(0).
Отже кожне раціональне число можна подати у вигляді нескінченного десяткового періодичного дробу. І кожен нескінчений періодичний дріб є записом деякого раціонального числа.
Поступово ми познайомились з іншими числами.
Якщо є раціональні числа, які ми можемо представити у вигляді дробу, то є і ті числа які не можемо представити у вигляді дробу, тобто не раціональні. Не раціональні числа назвали ірраціональними.
Ірраціональні числа ми не можемо представити у вигляді дробу. Ірраціональні числа – це числа, що не є раціональними, тобто не можуть бути виражені відношенням цілих чисел. Не можна представити у вигляді дробу ![]() , де m – ціле число,n – натуральне. Мають вигляд нескінчених десяткових дробів.
, де m – ціле число,n – натуральне. Мають вигляд нескінчених десяткових дробів.
Множина ірраціональних чисел – нескінчена множина, до якої належать усі числа, які не можна зависати у вигляді відношення цілого числа до натурального числа.
Найчастіше ірраціональні числа в школі це ті, корінь із яких ми не можемо обрахувати. Наприклад, ![]() ,
, ![]() ,
, ![]() , sin210
, sin210![]() Q - ці числа не можливо представити у вигляді дробу, де чисельник і знаменник є цілими числами. Тобто
Q - ці числа не можливо представити у вигляді дробу, де чисельник і знаменник є цілими числами. Тобто ![]() ,
, ![]() ,
, ![]() - це є ірраціональні числами.
- це є ірраціональні числами.
Коли ми робимо обчислення, ці числа ми залишаємо в такому вигляді. Якщо б вам зустрілось число ![]() = 2 – тобто ми можемо обрахувати. В даному випадку це число буде раціональним, і навіть цілим. А числа
= 2 – тобто ми можемо обрахувати. В даному випадку це число буде раціональним, і навіть цілим. А числа
![]() ,
, ![]() ,
, ![]() ми так і будемо залишати в такому вигляді. Але іноді необхідно знати їх приблизне значення. Їх необхідно запам’ятати.
ми так і будемо залишати в такому вигляді. Але іноді необхідно знати їх приблизне значення. Їх необхідно запам’ятати.
![]() ≈1,4;
≈1,4; ![]() ≈ 1,7;
≈ 1,7; ![]() ≈ 2,2. Це потрібно для того,щоб порівнювати з іншими числами. Щоб побачити в якому проміжку знаходиться це число. Але в ніякому разі не замінюйте цим значенням.
≈ 2,2. Це потрібно для того,щоб порівнювати з іншими числами. Щоб побачити в якому проміжку знаходиться це число. Але в ніякому разі не замінюйте цим значенням.
Є також число π (пи) ≈ 3,14159265... i так далi. – ірраціональне, з яким ви познайомились в 6 класі. Є число е ≈ 2,7.
І – “нерозумні ”(нераціональні) числа – нескінченні неперіодичні десяткові дроби .
Саме тому, що воно продовжується нескінченно i ніяких закономірностей у повторенні нема, в свiтi часто влаштовуються змагання з запам’ятовування знаків після коми цього числа.
Iррацiональнi числа — числа, що не є раціональними, тобто не можуть бути виражені відношенням цілих чисел. Мають вигляд нескінченних десяткових дробів.
Зверніть увагу! Будь – яке число можна представити у вигляді нескінченного неперіодичного десяткового дробу. ![]() = 2,333…
= 2,333…
Раціональні числа разом з ірраціональними числами складають множину дійсних чисел R. Найчастіші ви записували розв’язок рівняння, коли будь – яке число є коренем того рівняння, ми записуємо х ![]() R .
R .
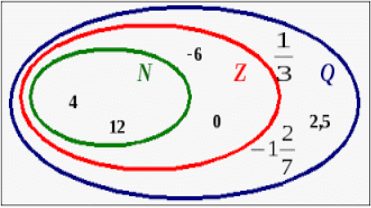
Дiйснi числа — множина, що складається з раціональних та iррацiональних чисел. Кожному числу ставиться у вiдповiднiсть одна точка на числовій прямій та навпаки, кожна точка числової прямої являє собою дійсне число.

Цей запис означає, що х належить множині дійсних чисел.
![]()
![]() Q, але
Q, але ![]()
![]() R.
R.
Підведемо підсумок.
Множина дійсних чисел – нескінчена множина, до якої належать усі раціональні та ірраціональні числа. R – множина дійсних чисел. R = Q![]() I.
I.
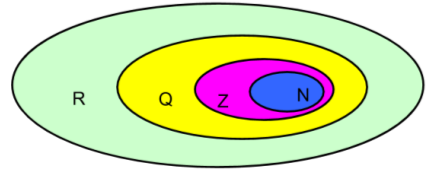
Між множинами N, Z, Q I R має місце співвідношення N![]() Z
Z![]() Q
Q![]() R.
R.
За допомогою кругів Ейлера можна зобразити входження числових множин одна в одну: N![]() Z
Z![]() Q
Q![]() R, тобто множина натуральних чисел N міститься в множині чисел Z, яка в свою чергу є підмножиною множини раціональних чисел Q, яка так само включається в множину дійсних чисел R.
R, тобто множина натуральних чисел N міститься в множині чисел Z, яка в свою чергу є підмножиною множини раціональних чисел Q, яка так само включається в множину дійсних чисел R.
Корисно запам’ятати.
Звичайно, позначення натуральні числа N, цілі числа Z, R раціональні числа необхідно запам’ятати.
До цієї інформації необхідно додати і запам’ятати взаємно обернені числа а і ![]() . Наприклад числа
. Наприклад числа ![]() і
і ![]() ; 2 і
; 2 і ![]() - добуток таким чисел дорівнює 1.
- добуток таким чисел дорівнює 1.
Протилежні числа а та – а. Наприклад числа 5 та – 5; ![]() та –
та – ![]() . Сума протилежних чисел дорівнює 0.
. Сума протилежних чисел дорівнює 0.
Досить часто путають поняття протилежні числа та взаємно обернені числа. Зверніть увагу!
Ще іноді в завданнях зустрічаються поняття простого і складного числа. Прості числа мають тільки два дільника. Діляться на одиницю і на саме число. Це 2,3,5,7,11,13,17,19…. Зверніть увагу! 2 – просте число.
Всі інші числа називаються складними.
Розв’язування завдання
1. Які з поданих чисел є натуральні, які – цілі, які – раціональні?
а) -![]() = -5; -0,2; 0 =
= -5; -0,2; 0 = ![]() ;
; ![]() ;
; ![]() ; 2,5;
; 2,5; ![]() = 5; 25.
= 5; 25.
N: ![]() ; 25.
; 25.
Z: -![]() ; 0;
; 0;![]() ; 25.
; 25.
Q = -![]() ; -0,2; 0;
; -0,2; 0; ![]() ; 2,5;
; 2,5; ![]() ; 25.
; 25.
2. Назвіть: найбільше ціле від’ємне число = -1;
найменше ціле додатне число = 1
3. Яке число протилежне до числа 1,5?1,5 = -1,5
Назвіть число обернене до числа 1,5. 1![]() =
=![]() =
= ![]() =
= ![]()
![]()
![]() .
.
4. Оберіть правильне твердження: 0![]() N; 0
N; 0![]() Z. 0
Z. 0![]() Z.
Z.
5. Порівняйте ![]() та 1,5.
та 1,5. ![]() ≈ 1,4
≈ 1,4![]() 1,4< 1,5.
1,4< 1,5.
6. Напишіть числа першого десятка.2,3,5,7.
Завдання зі збірника «Сучасна підготовка до ЗНО 2021»
Ю.О.Захарійченко
1. Обчисліть: а) (-4)3 + (-5)2 = -64 +25 = -39
б) (-9)2 + (-3)3 = 81- 27 = 54
2. Знайдіть значення виразу: а) 23∙17 + 77∙17 = 17(23 +77) = 17∙100= 1700
б) 37∙143 - 27∙143= 143(37 -27) = 143∙10 = 1430
3. Округліть число з точністю до сотень: а) 45758 ≈ 45800
б) 98830 ≈ 98800
4. Округліть число з точністю до десятих: а) 12,375 ≈ 12,4 б) 59,623 ≈59,6
Розв’язування завдання с ЗНО.
ЗНО 2010(пробне)
8. Яке з наведених чисел є раціональним?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
![]() = 0,8.
= 0,8.
ЗНО 2010. Завдання 26.
Установіть відповідність між числом (1 – 4) та множиною, до якої воно належить (А – Д).

Відповідь: 1 – Г, 2 – Д, 3 – А, 4 – В.
Це завдання дає можливість повторити повторений матеріал.
Можна працювати від лівої частини до правої і навпаки. В цьому прикладі начнемо з лівої частини.
1) 3,4 – А – множина парних натуральних чисел – ні.
Б – множина складених чисел( складені числа – натуральні числа)
– ні
В – множина цілих чисел, що не є натуральними числами – ні
Г– множина дробових чисел – так, 3,4 – це десятковий дріб.
2) ![]() – А – множина парних натуральних чисел – ні.
– А – множина парних натуральних чисел – ні.
Б – множина складених чисел( складені числа – натуральні числа)
– ні
В – множина цілих чисел, що не є натуральними числами – ні
Г – вже використали.
Д – множина ірраціональних чисел – ![]() =
= ![]() = 2
= 2![]() – так.
– так.
3) ![]() = 5 – А – множина парних натуральних чисел – ні.
= 5 – А – множина парних натуральних чисел – ні.
4) –13– Б – складені числа – натуральні числа – ні, отже
В – множина цілих чисел, що не є натуральними числами.
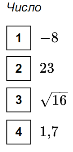

Відповідь: 1 – Б, 2 – Д, 3 – А, 4 – В.
ЗНО 2010(пробне)
7. Яке з наведених чисел є ірраціональним?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
2,7 |
![]() =
= ![]() = 2
= 2![]() . Усі інші числа(0,8; 1;2;2,7) можна записати у вигляді дробу
. Усі інші числа(0,8; 1;2;2,7) можна записати у вигляді дробу ![]() , де а – ціле, а b – натуральне.
, де а – ціле, а b – натуральне.
Задачі для самостійної роботи(числові множини,дроби, відсотки, модуль числа)
Пробне ЗНО 2016
1.![]() +
+ ![]()

![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() = 4
= 4![]()
ЗНО 2017
1. Запишіть число ![]() у вигляді десяткового дробу, округливши його до десятих.
у вигляді десяткового дробу, округливши його до десятих.
|
А |
Б |
В |
Г |
Д |
|
2,6 |
2,66 |
2,67 |
2,7 |
|
А – 2,6
17. Якщо а <1, то ![]() +
+ ![]() =
=

Завдання до теми «Числові вирази»
Розв’язування завдання
1. Які з поданих чисел є натуральні, які – цілі, які – раціональні?
а) -![]() ; -0,2; 0;
; -0,2; 0; ![]() ;
; ![]() ; 25;
; 25; ![]() ;
;
2. Назвіть найбільше ціле від’ємне число.
Найменше ціле додатне число.
3. Яке число протилежне до числа 1,5?
4. Оберіть правильне твердження: 0![]() N; 0
N; 0![]() Z.
Z.
5. Порівняйте ![]() та 1,5.
та 1,5.
6. Напишіть числа першого десятка.
Завдання зі збірника «Сучасна підготовка до ЗНО 2021»
Ю.О.Захарійченко
1. Обчисліть: а) (-4)3 + (-5)2 б) (-9)2 + (-3)3
2. Знайдіть значення виразу: а) 23∙17 + 77∙17 б) 37∙143 - 27∙143
3. Округліть число з точністю до сотень: а) 45758 б) 98830
4. Округліть число з точністю до десятих: а) 12,375 б) 59,623
5. Запишіть значення десятковим дробом: а) ![]() +
+ ![]() б)
б) ![]() +
+ ![]()
7. Обчисліть: а) ![]() б)
б) ![]()
8. Обчисліть: а) ![]() б)
б) ![]()
9. Обчисліть значення виразу: а) ![]() б)
б) ![]() :
: ![]()
10. Укажіть два послідовні цілі числа, між якими містяться значення виразу
а) 8:![]() б) 5:
б) 5:![]()
11. Розташуйте числа у порядку зростання
а) ![]() ;
; ![]() ;
; ![]() б)
б) ![]() ;
; ![]() ;
;![]()
12. Чому дорівнює значення виразу?
а) 815:319 б) 712:49
13. Обчисліть: а)![]() +1 б)
+1 б) ![]() -2
-2
14. Обчисліть: а) 5-2 + 1 б) 10-3 + 5-1
15. Обчисліть: а) 0,02-2 б) 0,1-3
ЗНО 2010(пробне)
8. Яке з наведених чисел є раціональним?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
1. ЗНО 2010. Завдання 26. а)
Установіть відповідність між числом (1 – 4) та множиною, до якої воно належить (А – Д).

б)
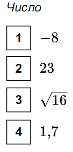

2. ЗНО 2015. Завдання 22(подібне).
1 ![]() А є неправильним
А є неправильним
2 ![]() Б є цілим числом
Б є цілим числом
3 0,2 В є не скоротним
4 ![]() Г є оберненим до числа 5
Г є оберненим до числа 5
Д більше за 0,5
ЗНО 2015. Завдання 22(ІІІ).
Установіть відповідність між твердженням про дріб (1 – 4) та дробом
(А – Д), для якого це твердження є правильним.

ЗНО 2015. Завдання 22(ІІІ).
Установіть відповідність між твердженням про дріб (1 – 4) та дробом
(А – Д), для якого це твердження є правильним.
![]()
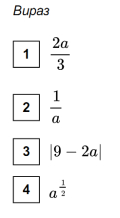
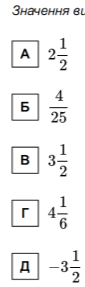
Пробне ЗНО 2016
1.![]() +
+ ![]()

ЗНО 2017
1. Запишіть число ![]() у вигляді десяткового дробу, округливши його до десятих
у вигляді десяткового дробу, округливши його до десятих
|
А |
Б |
В |
Г |
Д |
|
2,6 |
2,66 |
2,67 |
2,7 |
|
ЗНО 2015. Завдання 22(ІІІ).
Установіть відповідність між твердженням про дріб (1 – 4) та дробом
(А – Д), для якого це твердження є правильним.


ЗНО 2016. Завдання 22(ІІІ).
![]()
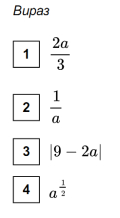
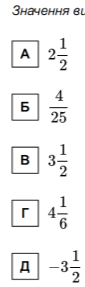


про публікацію авторської розробки
Додати розробку
