Презентація до уроку: Поняття похідної
Про матеріал
Презентація до уроку: Поняття похідної може бути використана під час дистанційного навчання в умовах війни для 10 - х класів з поглибленим вивченям математики.
Перегляд файлу
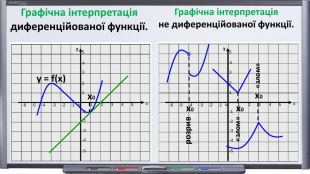
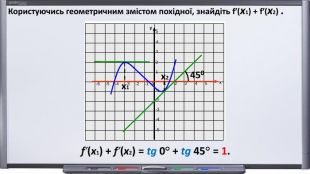
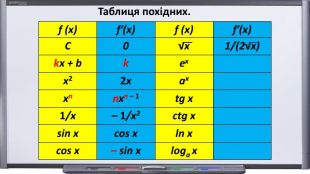
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


















































-

Пушкарук Алла
14.02.2025 в 10:59
Я в жасі від фото до презентації. Може автор не робив би те, з чого починався кожен урок в радянській школі, що все, дякуючи дорогому Леоніду Іллічу. Ми відходимо від радянщини, чи назад в СРСР? От за таке вчителів і не поважають. А зміст чудовий, окрім....
Загальна:
3.7
Структурованість
5.0
Оригінальність викладу
2.0
Відповідність темі
4.0
-

Kavinska Natalija
11.02.2025 в 22:57
Дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Харченко Ірина Вікторівна
10.09.2024 в 13:10
Дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Харченко Ірина Вікторівна
10.09.2024 в 13:10
Дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 1 відгук