Підсумкова контрольна робота 9 клас

Про матеріал

Підсумкова контрольна робота 9 клас складається з 20 варіантів . та з 8 завдань

Перегляд файлу

Підсумкова контрольна робота з алгебри

у 9-х класах

Пропонуються 20 варіантів. Кожен варіант складається з трьох частин, які відрізняються за складністю та формою тестових завдань.

У І частині контрольної роботи запропоновано п’ять завдань з вибором однієї правильної відповіді, що відповідають початковому та середньому рівням навчальних досягнень учнів. До кожного завдання подано чотири варіанти відповіді, з яких тільки один правильний. Завдання вважається виконаним правильно, якщо учень указав тільки одну літеру, якою позначений правильний варіант відповіді. Правильна відповідь за кожне із завдань 1-5 – оцінюється одним балом.

ІІ частина контрольної роботи складається з двох завдань, що відповідають достатньому рівню навчальних досягнень учнів. Розв’язання повинно мати короткий запис рішення без обґрунтування. Правильне розв’язання кожного із завдань цього блоку оцінюється двома балами.

ІІІ частина контрольної роботи складається з одного завдання, що відповідає високому рівню навчальних досягнень учнів, розв’язання якого повинно мати розгорнутий запис рішення з обґрунтуванням. Правильне розв’язання завдання цього блоку оцінюється трьома балами.

Сума балів нараховується за правильно виконані учнем завдання відповідно максимально можливій кількості запропонованих балів для кожного блоку (5; 4; 3-всього 12балів).

Учні загальноосвітніх класів виконують всі завдання крім завдання з позначкою «м».

Учні, які навчаються в класах з поглибленим вивченням математики виконують всі завдання І-ІІ частин, з ІІІ частини-тільки завдання з позначкою «м».

Учні загальноосвітніх класів виконують всі завдання крім завдання з позначкою «м».

Учні, які навчаються в класах з поглибленим вивченням математики, виконують всі завдання І-ІІ частин , а з ІІІ частини- тільки завдання з позначкою «м»

Контрольна робота розрахована на 45 хвилин. Роботи виконуються у зошитах або на окремих аркушах. При виконанні роботи необхідно вказати номер завдання. Текст завдань переписувати не обов’язково.

Примітка. У тексти завдань можна вносити корективи: збільшити (зменшити) кількість завдань або посилити (послабити) ступінь складності

Варіант 1

І частина (5 балів)

Завдання 1- 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть правильну відповідь. Правильна відповідь кожного завдання оцінюється одним балом.

№1. Оцініть периметр правильного трикутника зi стороною a см, якщо
2,1<a < 2,3.

А) 6,3<Р<6,9; Б) 6,3<Р<2,3; В) 2,1<Р<6,9; Г) 4,1<Р<4,6.

№2. Який з числових проміжків є розв’язком подвійної нерівності ?

А) В)

-4 1 x -4 1 x

Б) Г)

-4 1 x -4 1 x

№3. Скільки відсотків години складає 18 хвилин?

А) 30%; Б) 10,8%; В) 20%; Г) 10%.

№4. Яка пара чисел є розв’язком системи рівнянь ?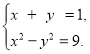

А) (–3; 4); Б) (5; – 4); В) (4; 3); Г) (–5; 4).

№5. У скриньці 5 чорних і 7 білих кульок. Із скриньки навмання виймається 1 кулька. Знайдіть ймовірність того, що ця кулька біла.

А); Б); В) ; Г) .

ІІ частина (4 бали)

Розв’язання завдань 6 – 7 повинно мати короткий запис рішення без обґрунтування. Правильне рішення кожного завдання оцінюється двома балами.

№6. Побудувати графік функції у = х² – 2х – 3. За графіком визначити:

а) значення у, якщо х = – 1,5;

б) значення х, якщо у = 5;

в) нулі функції.

№7. Знайдіть сьомий член і суму чотирнадцяти перших членів арифметичної прогресії, якщо перші чотири члени дорівнюють: 2; 6; 10; 14.

ІІІ частина (3 бали)

Розв’язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.

№8. Відстань між двома містами дорівнює 93 км. З одного міста в друге виїхав велосипедист, швидкість якого була на 3 км/год більша за швидкість першого. Велосипедисти зустрілись на відстані 45 км від першого міста. Знайдіть швидкість кожного велосипедиста.

№8^м Два спортсмени біжать по одній замкнутій доріжці стадіону. Швидкість кожного постійна, але перший пробігає всю доріжку на 10 с швидше, ніж другий. Якщо вони почнуть біг із спільного старту в одному напрямку, то ще раз зустрінуться через 720 с. Яку частину довжини всієї доріжки пробігає за секунду кожний спортсмен?

Варіант 2

І частина (5 балів)

№1. Оцiнiть периметр квадрату зi стороною b см, якщо 0,4< b <0,7.

А) 0,8<P<1,4; Б) 1,6<P<2,8; В) 1,2<P<2,1; Г) 0,4<P<2,8.

№2. Який з числових проміжків є розв’язком подвійної нерівності ?

А) В)

-1 4 x -1 4 x

Б) Г)

-1 4 x -1 4 x

№3. Скільки відсотків години складає 42 хвилини?

А) 70%; Б) 25,2%; В) 60%; Г) 14,2%.

№4. Яка пара чисел є розв’язком системи рівнянь ?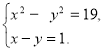

А) (10;-9); Б) (11; 10); В) (10; 9); Г) (9; 10)

№5. У скриньці 6 червоних і 5 синіх кульок. Із скриньки навмання виймається 1 кулька. Знайдіть ймовірність того, що ця кулька синя.

А) 0; Б); В) ; Г) .

ІІ частина (4 бали)

№6. Побудувати графік функції у = х²+ 2х – 3. За графіком визначити:

а) значення у, якщо х = – 1,5;

б) значення х, якщо у = 5;

в) нулі функції.

№7. Знайдіть шостий член і суму дванадцяти перших членів арифметичної прогресії, якщо відомі перші чотири члени: 4; 8; 12; 16.

ІІІ частина (3 бали)

№8. Із села А в село В, відстань між якими дорівнює 30 км, велосипедист проїхав з певною швидкістю, а повертався зі швидкістю на 3 км/год більшою і витратив на 30 хв менше, ніж на шлях з села А в село В. Знайдіть початкову швидкість велосипедиста.

№8^м Пароплав відходить від відстані А на припливі, йде вниз за течією 80км до ріки, далі по річці нагору проти течії до пристані В,затративши на весь шлях від А до В 18 год. Потім пароплав повертається назад. Час зворотного руху від В до А по тому ж шляху дорівнює 15год. Власна швидкість пароплава дорівнює 18км/год. Швидкість течії ріки 3км/год. Знайдіть відстань від пристані А до В і швидкість припливу.

Варіант 3

І частина (5 балів)

№1. Розв'яжіть систему нерівностей

А) (9;10); Б) (10;+ ∞); В) (– ∞;10); Г) (9;+ ∞).

№2. Знайдіть координати вершини параболи .

А) ; Б) ; В) ; Г) .

№3. Із свіжих груш отримують 18% сушених. Скільки взяли свіжих груш, якщо отримали 9 кг сушених?

А) 50 кг; Б) 500 кг; В) 200 кг; Г) 20 кг.

№4. Відриваємо один аркуш у новому відривному календарі високосного року. Яка з наведених подій є вірогідною?

А) на аркуші 1 вересня; Б) на аркуші число, яке менше за 32;

В) на аркуші 31 червня; Г) відірваний аркуш - вихідний день.

№5. Знайдіть медіану вибірки 9; 17; 26; 7; 14.

А) 17; Б) 14,6; В) 14; Г) 7.

ІІ частина (4 бали)

№6. Розв’яжіть систему нерівностей .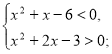

№7. Знайдіть чотири числа, що утворюють геометричну прогресію, якщо перший член більший від третього на 6, а другий менший від четвертого на 3.

ІІІ частина (3 бали)

№8. Із пункту А до пункту Б, відстань між якими 5 км, вийшов пішохід, а через 30 хв. слідом за ним виїхав велосипедист, швидкість якого на 10 км/год більша від швидкості пішохода. До пункту Б велосипедист приїхав на 10 хв. раніше від пішохода. Знайдіть швидкість велосипедиста і пішохода.

№8^м З пункту А і В,розташованих на відстані 100км, назустріч один одному одночасно виїхали два велосипедисти. Через 4 год вони зустрілися. Після зустрічі швидкість першого велосипедиста, що рухався з А до В, зросла на 5 км/год, а швидкість другого – на 10 км/год. Знайдіть початкову швидкість другого велосипедиста, якщо перший прибув до пункту В на 1год раніше, ніж другий – до пункту А.

Варіант 4

І частина (5 балів)

№1. Розв'яжіть систему нерівностей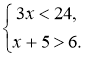

А) (1;8); Б) (8;11); В) (-;8); Г) (1; +).

№2. Знайдіть координати вершини параболи .

А) ; Б) ; В) ; Г) .

№3. Із свіжих слив отримують 35% сушених. Скільки сушених слив отримали з 52 кг свіжих?

А) 18 кг; Б) 18,2 кг; В) 1,8 кг; Г) 182 кг.

№4. Відриваємо один аркуш у новому відривному календарі не високосного року.

Яка з наведених подій є неможливою?

А) на аркуші число, яке менше за 32; Б) на аркуші 1 червня;

В) відірваний аркуш - вихідний день; Г) на аркуші 29 лютого.

№5. Знайдіть медіану вибірки 5; 3; 7; 4; 3.

А) 7; Б) 4,5; В) 4; Г) 3.

ІІ частина (4 бали)

№6. Розв’яжіть систему нерівностей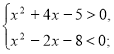

№7. Знайдіть чотири числа, що утворюють геометричну прогресію, якщо відомо, що перше число менше від третього на 36, а друге менше від четвертого на 12.

ІІІ частина (3 бали)

№8. Із пункту А до пункту Б, відстань між якими 10 км., виїхав велосипедист, а через 30 хв. слідом за ним – мотоцикліст, швидкість якого на 30 км/год. більша від швидкості велосипедиста. Знайдіть швидкості велосипедиста і мотоцикліста, якщо до пункту Б мотоцикліст приїхав на 15 хв. раніше від велосипедиста.

№8^м З пунктів А і В, розташованих на відстані 50км, назустріч один одному одночасно вийшли два пішоходи. Через 5 год вони зустрілися. Після зустрічі швидкість першого пішохода, що йде з А в В, зменшилася на 1 км/год, а швидкість другого зросла на 1 км/год. Знайдіть початкову швидкість першого пішохода, якщо він прибув до пункту В на 2 год раніше, ніж другий – у пункт А.

Варіант 5

І частина (5 балів)

№1. Виберіть правильне твердження. Вираз має зміст, якщо:

А) х(-∞;10]; Б) х[10;+∞); В) х(10;+∞); Г) х(-∞;10).

№2. На якому з малюнків зображено графік функції ?

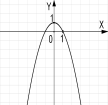
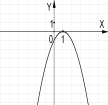
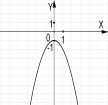
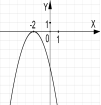А) Б) В) Г)

№3. На кожній грані куба написана одна з букв слова «ГРАФІК».

Яка ймовірність того, що куб упаде на грань з приголосною буквою?

А) ; Б) ; В) ; Г) .

№4. Знайдіть відсотковий вміст срібла в сплаві, якщо 200 г сплаву містять 42 г срібла.

А) 21%; Б) 210%; В) 84%; Г) 8,4%.

№5. Розв’яжіть систему рівнянь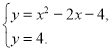

А) (– 4;4); Б) (–3;4); В) (4;4), (–2;4); Г) (2;4);

ІІ частина (4 бали)

№6. Розв’яжіть нерівність . Знайдіть її найбільший цілий розв’язок.

№7. Послідовність — арифметична прогресія. Знайдіть суму двадцяти перших її членів, якщо .

ІІІ частина (3 бали)

№8. Із двох міст, відстань між якими 900 км., вирушають назустріч один одному два потяги і зустрічаються на середині шляху. Визначте швидкість кожного потягу, якщо перший вийшов на 1 годину пізніше від другого із швидкістю більшою на 5 км/год, ніж швидкість другого потягу.

№8^м Із пункту А в пункт В, розташованого за 24км від А, одночасно вирушили велосипедист і пішохід. Велосипедист прибув до пункту В на 4 год раніше пішохода. Відомо, що, якби велосипедист їхав зі швидкістю меншою на 4 км/год, то на шлях з А до В він витратив би вдвічі менше часу, ніж пішохід. Знайдіть швидкість пішохода.

Варіант 6

І частина (5 балів)

№1. Виберіть правильне твердження. Вираз має зміст якщо:

А) х(7;+∞); Б) х(-∞;7); В) х(-∞;7]; Г) х[7;+∞) .

№2. На якому з малюнків зображено графік функції ?

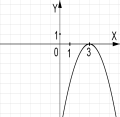
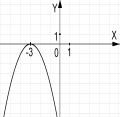
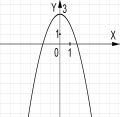
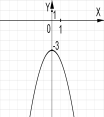А) Б) В) Г)

№3. На кожній грані куба написана одна з букв слова «ПРИЗМА».

Яка ймовірність того, що куб упаде на грань з голосною буквою?

А) ; Б) ; В) ; Г) .

№4. Знайдіть відсотковий вміст солі в розчині, якщо 500 г розчину містить 35 г солі.

А) 7%; Б) 175%; В) 17%; Г) 70%.

№5. Розв’яжіть систему рівнянь

А) (3;3); Б) (3; –3); В) (3;15); Г) (3;7).

ІІ частина (4 бали)

№6. Розв’яжіть нерівність . Знайдіть її найбільший цілий від’ємний розв’язок.

№7. В арифметичній прогресії , . Знайдіть суму перших п’ятнадцяти членів цієї прогресії.

ІІІ частина (3 бали)

№8. Два автомобілі виїжджають одночасно з одного міста до другого. Швидкість першого на 10 км/год. більша від швидкості другого, тому він прибуває на місце на 1 год. раніше. Визначте швидкість кожного автомобіля, якщо відстань між містами 560 км.

№8^м Двоє пішоходів одночасно виходять назустріч один одному з пунктів А і В і зустрічаються через 3 год. Якби вони обидва вийшли з пункту А у напрямку до В, при умові, що другий вийде на 3год пізніше від першого, то другий пішохід наздогнав би першого, пройшовши відстані від А до В. Скільки часу буде потрібно першому пішоходу на шлях із А до В?

Варіант 7

І частина (5 балів)

№1. Оцініть площу прямокутника зі сторонами a см и b см, якщо 2<a<2,5,
4<b<4,6.

А) 7<S<7,2; Б) 14,4<S<14; В) 14≤S≤14,4; Г) 8<S<11,5.

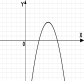
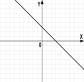
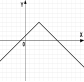
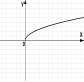№2. На якому з малюнків зображено графік квадратичної функції?

А) Б) В) Г)

№3. При якому значенні х вираз має зміст?

А) 4; Б) 3; В) – 1; Г) 10.

№4. Визначте кількість членів арифметичної прогресії (а_n), якщо , , .

А) 37; Б) 39; В) 43; Г) 45

№5. Середнє арифметичне двох чисел дорівнює 10,8. Відомо, що перше число

дорівнює 4,2. Знайдіть друге число.

А) 6,6; Б) 17,4; В) 16,4; Г) 7,5.

ІІ частина (4 бали)

№6. Доведіть, що система нерівностей не має розв’язків.

№7. Вкладник поклав до банку 3000 грн. під 9 % річних. Який нарощений капітал буде у вкладника через 3 роки?

ІІІ частина (3 бали)

№8. З пункту А в пункт В, відстань між якими 360 км, виїхали одночасно два автомобілі. Через 3 год. виявилося, що перший з них пройшов відстань на 30 км більше, ніж другий. Знайдіть швидкість кожного автомобіля, якщо на весь шлях перший автомобіль затратив на півгодини менше, ніж другий.

№8^м Два потяги виходять одночасно назустріч один одному з міст А і В, відстань між якими 112км. Через 56хв вони зустрічаються. Продовжуючи рух, перший потяг приходить в В на15хв раніше, ніж другий в А. Знайдіть швидкість кожного потягу.

Варіант 8

І частина (5 балів)

№1. Оцініть площу прямокутного трикутника з катетами m см и n см, якщо
2<m<4, 1<n<3.

А) 1,5<S<3,5; Б) 3<S<7; В) 1<S<6; Г) 2<S<12.

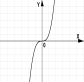
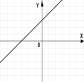
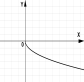
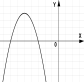№2. На якому з малюнків зображено графік квадратичної функції?

А) Б) В) Г)

№3. При якому значенні х вираз має зміст?

А) 4; Б) –3; В) 2; Г) –1.

№4. Визначте кількість членів арифметичної прогресії (а_n), якщо , , .

А) 94; Б) 95; В) 97; Г) 96.

№5. Середнє арифметичне числа 8,6 та невідомого числа дорівнює 20,4. Знайдіть невідоме число.

А) 32,2; Б) 10,8; В) 31,2; Г) 16,4.

ІІ частина (4 бали)

№6. Доведіть, що система нерівностей не має розв’язків.

№7. Вкладник поклав до банку 2000 грн. під 7 % річних. Який нарощений капітал буде у вкладника через 3 роки?

ІІІ частина (3 бали)

№8. Із двох пунктів, відстань між якими дорівнює 18 км, вийшли одночасно назустріч один одному 2 групи туристів і зустрілися через 2 год. Визначите, з якою швидкістю йшла кожна група, якщо на проходження всього шляху однієї з них треба було на 54 хв. більше, ніж іншій.

№8^м Два велосипедисти виїхали одночасно із пункту А. перший їхав зі швидкістю 24 км/год, а другий - 18 км/год. Через годину за ними виїхав автомобіль, який обігнав другого велосипедиста на 10хв раніше, ніж першого. Знайдіть швидкість автомобіля.

Варіант 9

І частина (5 балів)

№1. Порівняйте числа m та n, якщо m – n= – 3,5.

А) m ≥ n; Б) m ≤ n; В) m > n; Г) m < n.

№2. Який проміжок є розв’язком системи нерівностей ?

А) В)

2 5 x 5 x

Б) Г)

2 5 x 5 x

№3. 30% деякого числа дорівнюють 18. Знайдіть це число.

А) 90; Б) 48; В) 30; Г) 60.

№4. Розв’яжіть нерівність х² < 4.

А) –2< х < 2; Б) х < –2; х >2; В) х < 2; Г) х > 2.

№5. У класі 30 учнів. Навмання вибирають одного. Яка ймовірність того, що це буде

дівчинка, якщо дівчат у класі 14?

А); Б) ; В); Г) .

ІІ частина (4 бали)

№6. Побудуйте графік функції . Знайдіть

а) при яких значеннях аргументу значення функції додатні;

б) при яких значеннях аргументу функція спадає.

№7. Подайте число 2,3 (24) у вигляді звичайного дробу.

ІІІ частина (3 бали)

№8. Вкладник поклав до банку на два різні рахунки загальну суму 15 000 грн. По першому з них банк виплачує 7 % річних, а по другому – 10% річних. Через рік вкладник отримав 1200 грн. відсоткових грошей. Скільки гривень він поклав на кожен рахунок?

№8^м Двоє бігунів стартували один за іншим з інтервалом 2хв. Другий бігун наздогнав першого на відстані 1км від старту, а пробігши від старту 5км, він повернув назад і зустрівся з режим бігуном. Ця зустріч відбулася через 20хв після старту першого бігуна. Знайдіть швидкість другого бігуна.

Варіант 10

І частина (5 балів)

№1. Порівняйте числа a та b, якщо a – b = – 5.

А) a > b; Б) a < b; В) a ≤ b; Г) a ≥ b.

№2. Який проміжок є розв’язком системи нерівностей

А) В)

3 7 x 7 x

Б)

Г)

3 7 x 3 x

№3. 18% деякого числа дорівнюють 90. Знайдіть це число.

А) 50; Б) 500; В)5000; Г) 1620.

№4. Розв’яжіть нерівність х² > 9.

А) х > 3; Б) -3< х < 3; В) х < -3; х >3; Г) х < 3.

№5. У класі 24 учні. Навмання вибирають одного. Яка ймовірність того, що це

хлопчик, якщо хлопців у класі 10?

А) ; Б); В) ; Г).

ІІ частина (4 бали)

№6. Побудуйте графік функції . Знайдіть:

а) при яких значеннях аргументу значення функції від’ємні;

б) проміжки зростання функції.

№7. Подайте число 3,5(71) у вигляді звичайного дробу.

ІІІ частина (3 бали)

№8. Вкладник поклав до банку 10 000 грн. За перший рік йому було нараховано певний відсоток річник, а другого року банківський відсоток було збільшено на 2 %. У кінці другого року на рахунку було 11 880 грн. Скільки відсотків становила банківська ставка у перший рік?

№8^м Двоє лижників стартували на дистанції 10км один за одним з інтервалом у 6 хв. Другий лижник наздогнав першого на відстані 2 км від старту. Дійшовши до повороту на позначці 5км, другий лижник повернув назад і зустрів першого на відстані 1км від повороту. Знайдіть швидкість першого лижника.

Варіант 11

І частина (5 балів)

№1. Відомо, що 2<a<5, 8<b<10. Оцініть значення виразу a + b.

А) 7<a+b<18; Б) 10a+b15; В) 10<a+b<15; Г) 12<a+b<13.

№2. Який з проміжків є розв’язком нерівності 7 + 2x > 9?

А) x [8;+]; Б) x [1;+); В) x (1;+); Г) x (– ;1).

№3. У шкільному концерті беруть участь 16 учнів 5 класу, 14 учнів 6 класу, 10 учнів 4 класу. Яка ймовірність того, що з черговим номером буде виступати учень 4 класу?

А) 0,25; Б) 4; В) ; Г) 0,5.

№4. Знайдіть суму чотирьох перших членів геометричної прогресії (b_n), якщо = , а =.

А) ; Б) 8; В) ; Г) .

№5. Який відсотковий вміст води в меді, якщо 400 г меду містить 68 г води?

А) 15%; Б) 16%; В) 18%; Г) 17%.

ІІ частина (4 бали)

№6. Графіку функції у=2х² + bх + 3 належить точка А(–1;6). Знайдіть b.

№7. Розв’яжіть систему рівнянь .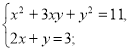

ІІІ частина (3 бали)

№8. Двоє робітників виконали разом певну роботу за 12 год. Якби спочатку перший виконав половину цієї роботи, а потім другий решту, то вся робота була б завершена за 25 год. За який час міг би виконати цю роботу кожний робітник окремо?

№8^м У січні продуктивність праці в цеху заводу підвищилася на 10% у порівнянні з плановою, а в лютому підвищилася ще на 6% порівняно із січнем. На скільки відсотків цех перевиконав план випуску виробів за ці два місяці? (Передбачається, що щомісячний план на ці два місяці однаковий)

Варіант 12

І частина (5 балів)

№1. Відомо, що 3,2< x <4, 4< y <7,5. Оцініть значення виразу xy.

А) 16< xy <28; Б) 12,8< xy <30; В) 13,8< xy <29; Г) 14< xy <32.

№2. Який з проміжків є розв’язком нерівності 3 + 3x < 12?

А) x (– ;3); Б) x (– ;3]; В) x (– ;5); Г) x (3;+).

№3. У вазі стоїть 5 білих, 3 червоних і 7 рожевих хризантем. Знайдіть ймовірність того, що навмання взята хризантема буде рожевою.

А); Б); В); Г).

№4. Знайдіть суму п’яти перших членів геометричної прогресії (b_n),
якщо = – 1, а = – 2.

А) 11; Б) -11; В) ; Г) .

№5. Який відсотковий вміст заліза в залізній руді, якщо в 400 г залізної руди

міститься 284 г заліза?

А) 71%; Б) 7,1%; В)0,71 %; Г) 0,071%.

ІІ частина (4 бали)

№6. Графіку функції у= – х² – 3х + с належить точка А(– 2;5). Знайдіть с.

№7. Розв’яжіть систему рівнянь .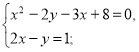

ІІІ частина (3 бали)

№8. При спільній роботі двох тракторів різної потужності поле було оброблено за 8 днів. Якби половину поля обробив спочатку один трактор, то при подальшій спільній роботі двох тракторів уся робота була б закінчена за 10 днів. За скільки днів можна було б зорати усе поле кожним трактором окремо?

№8^м У січні завод виконав план випуску продукції на 105%, а в лютому дав продукції на 4% більше, ніж у січні. На скільки відсотків завод перевиконав план випуску продукції за ці два місяці? (Передбачається, що щомісячний план на ці два місяці однаковий)

Варіант 13

І частина (5 балів)

№1. Знайдіть допустимі значення змінної ;

А) (;+∞); Б) [;+∞); В) (– ∞;); Г) (– ∞;].

№2. Не виконуючи побудови, встановіть, через яку з даних точок проходить графік

функції у=х²–3х–10.

А) А(5;0); Б) В(–5;0); В) С(3;10); Г) D(–3;10).

№3. Для поповнення шкільної бібліотеки було витрачено 2400 грн., з яких 18% – на

книги з математики. Скільки грошей було витрачено на придбання книг з

математики?

А) 400 грн.; Б) 420 грн.; В) 432 грн.; Г) 408грн.

№4. Яка пара чисел є розв’язком системи рівнянь ?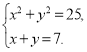

А) (–3; 4); Б) (3; – 4); В) (3; 4); Г) (–3; –4).

№5. Знайдіть середнє геометричне чисел 5 і 49.

А) 49; Б); В); Г) 7.

ІІ частина (4 бали)

№6. Розв’яжіть нерівність і знайдіть її найбільший від’ємний і
найменший додатний цілий розв’язок.

№7. Знайдіть чотири числа, що утворюють геометричну прогресію, третій член якої

більший від першого на 9, а другий більший від четвертого на 18.

ІІІ частина (3 бали)

№8. Побудуйте графік функції і за його допомогою визначте нулі

функції, проміжки монотонності, область значень функції.

№8^м Щоб виконати все замовлення першому робітнику потрібно часу на 25% більше, ніж другому, а третьому – в рази більше, ніж першому. Працюючи разом, три робітники виконають все замовлення за 5 днів. За скільки днів виконає все замовлення кожен робітник окремо?

Варіант 14

І частина (5 балів)

№1. Знайдіть допустимі значення змінної ;

А) [–;+∞); Б) (–;+∞); В) [;+∞); Г) [;+∞].

№2. Не виконуючи побудови, встановіть, через яку з даних точок проходить графік

функції у=х²–х–12.

А) А(3;0); Б) С(–3;0); В) D(4;2); Г) В(0;12).

№3. На придбання спортивного інвентарю було витрачено 1800 грн., з яких 26% - на футбольні м’ячі. Скільки грошей було витрачено на м’ячі?

А) 480 грн.; Б) 468 грн.; В) 454 грн.; Г) 420 грн.

№4. Яка пара чисел є розв’язком системи рівнянь ?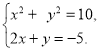

А) (1; –3); Б) (–3; 1); В) (– 4;3); Г) (3; –1).

№5. Знайдіть середнє геометричне чисел 5 і 36.

А) 36; Б) 6; В) ; Г) .

ІІ частина (4 бали)

№6. Розв’яжіть нерівність і знайдіть її найбільший від’ємний і найменший додатний цілий розв’язок.

№7. Знайдіть чотири числа, що утворюють геометричну прогресію, перший член якої

менший за третій на 24, а другий більший від четвертого на 8.

ІІІ частина (3 бали)

№8. Побудуйте графік функції і за його допомогою визначте нулі

функції, проміжки монотонності, область значень функції.

№8^м Щоб зорати все поле першому трактору потрібно на 50% більше часу, ніж другому, а третьому – в рази менше часу, ніж першому. Працюючи разом, три трактори зорють все поле за 4 дні. За скільки днів зоре все поле кожен трактор окремо?

Варіант 15

І частина (5 балів)

№1. Розв’яжіть подвійну нерівність – 8< 2x <10;

A) (– 4;5); Б) [– 4;5]; В) (– 6;8); Г) (4;5).

№2. Параболу у =2х² перенесли вліво на 3 одиниці. Задайте формулою функцію, графік якої отримаємо в результаті таких перетворень.

А) у =2х²+3; Б) у =2(х–3)²; В) у =2(х+3)²; Г) у =2х²–3.

№3. 25% деякого числа дорівнюють 103. Знайдіть це число.

А) 412; Б) 25,75; В) 2,575; Г) 41,2.

№4. Знайдіть середнє значення вибірки 9; 7; 2; 1; 1.

А) 2; Б) 4; В) 1; Г) 9.

№5. Обчисліть суму перших десяти членів арифметичної прогресії, перший член якої а₁ = 8, а різниця d = 6.

А) 620; Б) 62; В) 350; Г) 750.

ІІ частина (4 бали)

№6. Побудуйте графік функції . Знайдіть

а) при яких значеннях аргументу значення функції додатні;

б) при яких значеннях аргументу функція спадає.

№7. Знайдіть область визначення функції .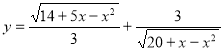

ІІІ частина (3 бали)

№8. Розв’яжіть задачу.

З пунктів А і В, відстань між якими дорівнює 27 км, одночасно назустріч один

одному вийшли два пішоходи і зустрілися через 3 год. Пішохід, що вийшов з А,

приходить в В на 1 год. 21 хв. раніш, ніж другий приходить в А. Знайдіть швидкість

кожного пішохода.

№8^м Три токарі, працюючи разом можуть виконати все замовлення за 24год. Перший токар може виконати все замовлення за час, що на 50% більший, ніж час, потрібний для цього другому токарю. Третій токар буде працювати в рази довше, ніж другий. За скільки годин може виконати все замовлення кожен токар?

Варіант 16

І частина (5 балів)

№1. Розв’яжіть подвійну нерівність ;

А) ; Б) ; В) ; Г) .

№2. Параболу у = –х² перенесли вправо на 1 одиницю. Задайте формулою функцію, графік якої отримаємо в результаті таких перетворень.

А) у = – (х+1)²; Б) у = – х²+1; В) у = – (х–1)²; Г) у = – х²–1.

№3. 20% деякого числа дорівнюють 32. Знайдіть це число.

А) 160; Б) 640; В) 64; Г) 1600.

№4. Знайдіть середнє значення вибірки 2; 1; 3; 5; 7; 6.

А) 7; Б) 24; В) 4; Г) 3.

№5. Знайдіть суму перших восьми членів арифметичної прогресії, різниця якої

d = 10, а перший член а₁ = 2.

А) 296; Б) 72; В) 286; Г) 576.

ІІ частина (4 бали)

№6. Побудуйте графік функції і знайдіть:

а) при яких значеннях аргументу значення функції від’ємні;

б) проміжки зростання функції.

№7. Знайдіть область визначення функції .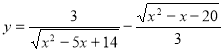

ІІІ частина (3 бали)

№8. Розв’яжіть задачу.

Два велосипедисти виїхали одночасно з пункту А в пункт В, відстань між якими 36

кілометрів. Через 2 год. один велосипедист обігнав другого на 6 км. Знайдіть

швидкість кожного велосипедиста, якщо відомо, що перший прибув в В на 36 хв.

раніш, ніж другий?

№8^м Робітник може виконати деяке замовлення на 2 год швидше, ніж учень. Через 2 год 20 хв. після того, як до виконання замовлення приступив робітник, йому став допомагати учень, і вони виконали частину замовлення, що залишилася, за 1год. Скільки часу виконує замовлення робітник, працюючи один?

Варіант 17

І частина (5 балів)

№1. Розв’язати нерівність 4х – 3 < 2х + 7.

А) х(–∞;5]; Б) х(–∞;5); В) х(5;+∞); Г) х[5;+∞).

№2. Знайдіть абсциси точок перетину параболи у =х²–10х–24 з віссю .

А) 12; –2; Б) 6; –4; В) –12; 2; Г) –6; 4.

№3. Скільки відсотків складає число 24 від числа 120?

А) 20%; Б) 13%; В) 2%; Г) 22%.

№4. Який з проміжків є розв’язком нерівності (х – 3)(х – 1) ≤ 0?

А) (-∞; 1)(3; +∞); Б) [1; 3]; В) (-∞; 1][3; +∞); Г) (1; 3).

№5. Визначте вид події: Подія А – учень накреслив трикутник, сума внутрішніх

кутів якого дорівнює 185°.

А) вірогідна; Б) неможлива;

В) випадкова; Г) вірогідна, але випадкова.

ІІ частина (4 бали)

№6. Знайдіть додатні значення у, що задовольняють системі нерівностей

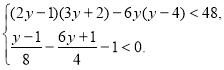
№7. Знайдіть середнє значення, моду і медіану вибірки: 7; 1; 3; 4; 9; 7; 11; 8; 6.

ІІІ частина (3 бали)

№8. Сума трьох чисел, що утворюють арифметичну прогресію, дорівнює 3. Якщо до першого і третього членів додати по 4, а до другого додати 3, то одержані числа утворять геометричну прогресію. Знайдіть ці числа.

№8^м Майстер та його учень мали виконати роботу до певного терміну. Проте, коли було виконано половину роботи, учень занедужав, і майстер, залишившись один, закінчив роботу з запізненням на 2 дні. За скільки днів міг би виконати всю роботу кожний з них, працюючи окремо, якщо майстру на це треба на 5 днів менше, ніж учню?

Варіант 18

І частина (5 балів)

№1. Розв’язати нерівність 5 – 3х < 17 – 5х.

А) х(6;+∞); Б) х(–∞;6); В) х(–∞;6]; Г) х[6;+∞).

№2. Знайдіть абсциси точок перетину параболи у =х²–6х–40 з віссю .

А) –10; 4; Б) –5; 8; В) 10; –4; Г) 5; –8.

№3. Скільки відсотків складає число 25 від числа 125?

А) 10%; Б) 15%; В) 20%; Г) 25%.

№4. Який з проміжків є розв’язком нерівності (х – 2)(х – 4) < 0?

А) (–∞; 2)(4; +∞); Б) [2; 4]; В) (–∞; 2][4; +∞); Г) (2; 4).

№5. Визначте вид події: Подія А – учень накреслив чотирикутник, сума внутрішніх

кутів якого дорівнює 270°.

А) вірогідна; Б) випадкова;

В) неможлива; Г) вірогідна, але випадкова.

ІІ частина (4 бали)

№6. Знайдіть від’ємні значення у , що задовольняють системі нерівностей

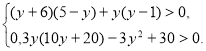
№7. Знайдіть середнє значення, моду і медіану вибірки: 2; 8; 4; 6; 9; 11; 8; 3; 12.

ІІІ частина (3 бали)

№8. Сума трьох чисел, що утворюють арифметичну прогресію, дорівнює 24. Якщо до першого і третього членів додати по 2, а друге залишити без зміни, то отримані числа утворять геометричну прогресію. Знайдіть ці числа.

№8^м Один робітник може виконати все замовлення на 7год швидше, ніж другий. Перший робітник за 4год виконує на замовлення більше, ніж другий за 3год. За скільки годин виконають два робітники все завдання, працюючи разом?

Варіант 19

І частина (5 балів)

№1. Відомо, що 2<a<5, 8<b<10. Оцініть значення виразу .

А) <<; Б) <<; В) 2<<4; Г)16<<50.

№2. Яке число є розв’язком нерівності ?

А) 4; Б) 3; В) 9; Г) 0.

№3. Вкажіть графічне розв’язання даної системи рівнянь

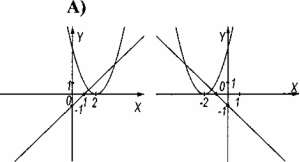
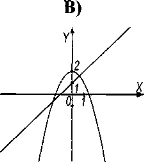
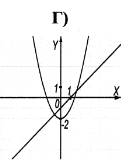
№4. Знайти восьмий член геометричної прогресії (b_n), якщо = 2, = – 2?

А) – 256; Б) 256; В) – 12; Г) 16.

№5. Знайдіть ймовірність того, що при одному підкиданні грального кубика випаде

не більше 3 балів.

А) 0,5; Б) 0; В) 1; Г) 2.

ІІ частина (4 бали)

№6. Розв’яжіть систему нерівностей

№7. Скільки кілограмів 30% і скільки кілограмів 55% сплавів міді треба взяти, щоб

отримати 30 кг 40% сплаву?

ІІІ частина (3 бали)

№8. Побудуйте графік функції і за його допомогою визначте нулі

функції, проміжки монотонності, область значень функції.

№8^м Майстер може виконати все замовлення на 16 год швидше, ніж його учень. Майстер за 6год виконує на замовлення більше, ніж учень за 8год. За скільки годин виконають все завдання майстер і учень, працюючи разом?

Варіант 20

І частина (5 балів)

№1. Відомо, що 3<x<4,2 і 2,1<y<5. Оцініть значення виразу x - y.

А) 7,2<x-y<8,3; Б) 6,1<x-y<8,2; В) -0,8<x-y<0,9; Г) -2<x-y<2,1.

№2. Яке число є розв’язком нерівності ?

А) 4; Б) 3; В) 9; Г) 10.

№3. Вкажіть графічне розв’язання даної системи рівнянь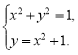

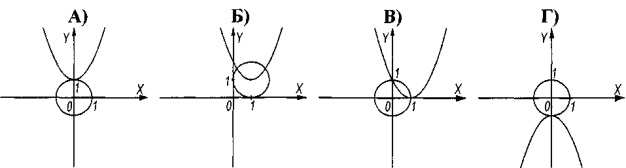
№4. Знайти четвертий член геометричної прогресії (b_n), якщо = 4, q=?

А) ; Б) ; В) ; Г) .

№5. Знайдіть ймовірність того, що при одному підкиданні грального кубика випаде не менше 4 балів.

А) 1; Б) 3; В) 0; Г) 0,5.

ІІ частина (4 бали)

№6. Розв’яжіть систему нерівностей

№7. Після того, як змішали 60% і 20% розчини кислоти, отримали 800 г 40% розчину.

Скільки грамів кожного розчину змішали?

ІІІ частина (3 бали)

№8. Побудуйте графік функції і за його допомогою визначте нулі

функції, проміжки монотонності, область значень функції.

№8^м Майстер і учень, працюючи разом, закінчують завдання на 1 годину раніше, ніж майстер, працюючи один, але на 0,5год пізніше, ніж майстер і два учні. За який час виконають завдання два майстри й учень?

Звіт з алгебри

Місто (район)_________________________________________

Табл.1. Кількісний звіт

Кількість учнів	Писало	Результати
		І рівня		ІІ рівня		ІІІ рівня		ІV рівня
		кількість	%	кількість	%	кількість	%	кількість	%

Аналітичний звіт: матеріал, засвоєний учнями якісно; допущені типові помилки, причини та шляхи їх подолання.

Примітка. Якщо до тексту завдань були внесені корективи, то необхідно надіслати змінені тексти з обґрунтуванням необхідності такого кроку.

Виконавець підпис прізвище, ініціали

Середня оцінка розробки

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0

Загальна:

5.0

Всього відгуків: 1

Оцінки та відгуки

Грінєвич Ганна Ігорівна 18.05.2021 в 23:25

Чудовий набір завдань) Дякую - моєму 9му класу було дуже доречно потренуватися напередодні річної контрольної роботи))

Загальна:

5.0

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0

doc

Завантажити

Зберегти на потім

Додав(-ла)

Бахмат Наталія

Пов’язані теми

Алгебра, Контрольні роботи

Додано

18 травня 2021

Переглядів

4838

Оцінка розробки

5.0 (1 відгук)