Підсумкова контрольна робота для учнів 11-х класів

Підсумкова контрольна робота з математики 11 клас 

І варіант

1.Реконструкція дороги дозволила зменшити час поїздки на маршрутці з одного мікрорайону міста в інший з 50 хв. до 40 хв. Обчисліть , на скільки відсотків зменшився час поїздки на маршрутці між цими мікрорайонами.

4.     Установіть відповідність між тілом обертання, заданим умовою (1-4), та формулою (А-Д) для обчислення його об’єму V.

1)     квадрат зі стороною 𝑎 обертається навколо прямої, що  проходить через сторону цього квадрата.

2)     Прямокутний рівнобедрений трикутник із катетом 𝑎 обертається навколо прямої, що проходить   через катет цього трикутника

3)     Прямокутний рівнобедрений трикутник із катетом 𝑎 обертається навколо прямої, що проходить через вершину гострого кута цього трикутника перпендикулярно до одного з його катетів.

4)     Круг, радіус якого дорівнює , обертається навколо прямої, що проходить через центр цього круга.

А.  

5.     Розв’яжіть систему рівнянь   

6.     Обчисліть площу фігури, обмеженої лініями у = х² + 2 та у = х + 4

7.     У шаховому турнірі брали участь 6 шахістів. Учасники турніру зіграли кожен з кожним тільки по одній партії. Знайдіть, скільки всього шахових партій було зіграно на цьому турнірі.

8.     Площа осьового перерізу конуса дорівнює 12см², а його об’єм дорівнює 16𝜋см³. Знайдіть відношення площі повної поверхні конуса до площі його основи. Відповідь запишіть у вигляді десяткового дробу. 9. Розв’язати рівняння log₆(𝑥 − 3) + log₆(𝑥 − 8) = 2

ІІ варіант

                                                                          1                              

1.     Спростіть вираз  

2.     Укажіть якому з наведених проміжків належить корінь рівняння 5^4−5𝑥 = 1

3.

2

4.     У прямокутній декартовій системі координат  𝑥𝑦𝑧  у просторі задано точку М(1;-4;8). Установіть відповідність між початком речення (1-4) та його закінченням (А-Д) так, щоб утворилося правильне твердження.

1)     Відстань від точки М до площини 𝑥𝑦  дорівнює

2)     Відстань від точки М до початку координат дорівнює

3)     Відстань від точки М до осі 𝑧 дорівнює

4)     Відстань від точки М до точки N(1;0;8) дорівнює

А. 1     Б. 4     В. √17   Г. 8      Д. 9

5.     В урні знаходяться 100 пронумерованих жетонів (від 1 до 100). Знайдіть імовірність того , що номер навмання витягнутого з урни жетона не містить цифру три.

6.     Сторона основи правильної чотирикутної піраміди дорівнює 6см, а бічна грань нахилена до площини основи під кутом 60⁰. Знайдіть площу повної поверхні піраміди.

7.     Знайти значення виразу  6^{2log69−log64}

8.     Розв’яжіть систему рівнянь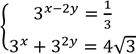  

9.     Розв’язати рівняння log₆(𝑥 − 3) + log₆(𝑥 − 8) = 2