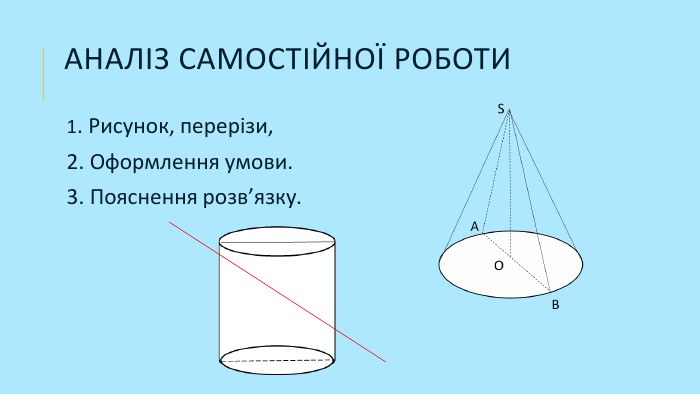
Презентація "Розв'язання задач на кулю"
Про матеріал
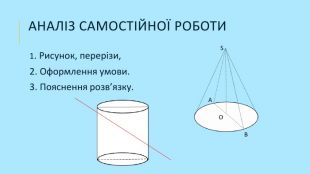
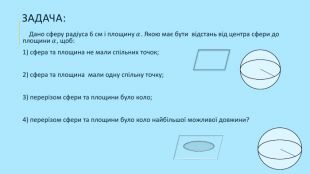
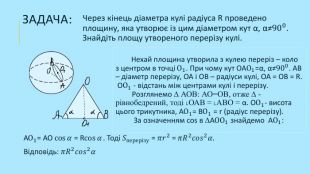
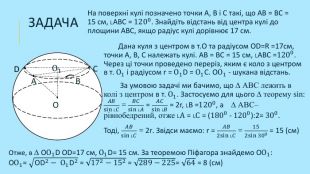
Формування практичних навичок розв'язування задач на застосування понять куля, сфера, перерізи кулі. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку