Підсумкова контрольна робота з алгебри для учнів 9 класу

Підсумкова контрольна робота

Варіант 1

1. Розв'яжіть нерівність  х²-49.

       А)  (-∞;7);     Б) (-∞;-7] υ [7;+∞);     В)(-∞;-7)υ(7;+∞);     Г)(-7;7)

2. У ящику є 30 пронумерованих від 1 до 30 жетонів. Яка ймовірність того, що номер навмання взятого жетона буде кратним числу 7?

А) ;       Б) ;       В) ;       Г) .

3. . Чому дорівнює четвертий член геометричної прогресії, якщо її перший член b₁=6, а знаменник q=-2.

           А) -48;  Б) 48;  В) 24;  Г) -24.

4. . На малюнку зображено графік функції  у=х²-2х-3.

    Розв'яжіть нерівність х²-2х-3 0.                 

    А) (-∞;-1)υ(3;+∞);       Б) [-1;3];     В) (-∞;-1]υ[3;+∞);

     Г) [3;+∞)

5. . Розв'яжіть  систему  нерівностей    

          А) х<2;         Б)  х<-2;        В) 1<х<2;          Г) -2<х<2

6.  (а_n) – арифметична прогресія, а₁ = -2, а₃= 4.  Знайдіть різницю прогресії.

     А) -6;              Б) 3;                  В) 6;                    Г) 1.

Достатній рівень навчальних досягнень

7. У кінотеатрі в кожному наступному ряді на 4 місця більше ніж у попередньому, а всього місць у залі – 640. Скільки рядів у кінотеатрі, якщо у першому ряді 10 місць.

 8. Розв'яжіть систему рівнянь: 

Високий рівень навчальних досягнень

9. Знайти область визначення функції  у=

Підсумкова контрольна робота

Варіант 1

1. Розв'яжіть нерівність    х² – 16 ≤0

      А) (-4;4);    Б) [-4;4];   В) (-∞;4];     Г) (-∞;4]υ[4;+∞).

2. У ящику є 20 кубиків, пронумерованих від 1 до 20. Яка ймовірність того, що номер навмання взятого з ящика кубика буде кратним числу 7?

           А) ;        Б) ;       В)  ;      Г)    

3. У геометричній прогресії (b_n)   b₃ =28,   q=-2.   Знайдіть  b_1.

             А) -14;     Б) 14;         В) -7;       Г) 7.

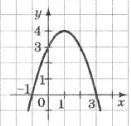
4. . На малюнку зображено графік функції

 у=-х²+2х+3.  

    Розв'яжіть нерівність  -х²+2х+3>0.

     А) (-∞;-1)υ(3;+∞);             Б) [-1; 3];               В)  (-1;0);  Г) (-1;3)

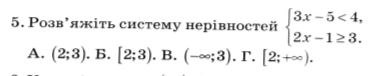
5.

6. (a_n)- арифметична прогресія, а₂=5, d=-3. Знайдіть а₄.

           А)-4;   Б) -1;   В) 2;   Г) 8.

Достатній рівень навчальних досягнень

7. Знайдіть суму десяти перших членів арифметичної прогресії (а_п), якщо а₁=14 , а₄=23.

8. Розв'яжіть систему рівнянь: 

Високий рівень навчальних досягнень

9. Побудуйте графік функції у=х²-4х-5. Користуючись графіком знайдіть:

1. Множину розв’язків нерівності   х²-4х-5≤0;

                  2)    Проміжок зростання функції.