Середній рівень

1.    Яке з поданих нерівностей вірно?

А) sin100^o  cos160^o                  В)   sin100^o  tg100^o Б)  cos100^o  sin10^o                Г)   cos100^o  cos180^o

x

2.    Розв’язати нерівність ^_ 9 ^_  27

                                                                    25     125

      А)  (;2]               Б)  [2;)                     В) (;1,5]                 Г) [1,5;)

3.    Спростити вираз  ctg(^)  tg(2)

2

      А)  2ctg              Б) 2tg                      В) 1                            Г) 0

4.    Розв’язати нерівність 4^3x7 16 А) 1;  Б) 113 ;  В) 3;  Г)  53;



 

5.    Обчислити   log₃ 36 log₃ 4

      А) 4;                       Б) 3;                           В) 2;                           Г) log₃ 32

6.    Знайти бічну сторону рівнобедреного трикутника, периметр якого дорівнює 66см, а бічна сторона на 12см менше основи.

      А) 28см                 Б) 16см                     В) 18см                     Г) 30см

 

Достатній  рівень

 

1.     Розв’язати рівняння  x^lgx2 1000

 

2.     Знайти область визначення функції:

      f (x)  2x₂  _x3

 

Високий  рівень

 

 a 9⁶ a3⁶ a

1.  Обчисліть значення виразу   при  a8 .

³ a 3⁶ a

 

2.  Висота прямокутного паралелепіпеда 8 дм, довжини двох сторін основи і діагональ паралелепіпеда утворюють арифметичну прогресію з різницею 5 дм. Знайти сторони основи і діагональ

 

 

 

 

 

 

 

 

 

Середній рівень

1. Знайти нерівність, у якої множина рішень є множиною дійсних чисел.

А) 2x  1                         Б) 2x  1                   В) 2x 1 2. Розв’язати рівняння   ctg3x  0       А)  n,n Z                                     В) n,nZ 2       Б)   n ,n Z              -                    Г) n ,n Z                    6      3                                                      3                                                  1        3

Г) 2x 1

 ³ 3^

3. Обчислити   

                                              3     

        А) 1                      Б) 9                    В)               Г)  

1. 4. Обчислити 6sin  3cos3                                                       6              2
А) 0                      Б) 3                В) 6		Г) 3 3

 

5.  Розв’язати  рівняння 46^{log6 x}  5  x²

      А) -5;1                 Б) -1; 5                      В) 1                Г)5

6.  У трикутнику FPK P  90^o,F  60^o, PF=12см.  Знайти інші  сторони трикутника.

      А) 12см,12 3см                            В) 24 3см,24см

      Б) 24см,12 3см                            Г) 6 3см,6см

 

Достатній  рівень

 

1.      Розв’язати рівняння 4^x2  64^x1  70

2.      Розв’язати рівняння cos2xsinx0

 

Високий  рівень

 

1lg² 5

1.    Обчисліть значення виразу  lg5

2lg 10 lg5

 

2.    В правильній чотирикутній піраміді відстань від центра основи до бічної грані 12 см.    Бічна грань утворює з основою кут, рівний 30º. Знайти сторону основи

 

 

 

 

 

 

 

 

 

Середній рівень

1. Розв’язати нерівність  53x4  25
А)  2;             Б) ;2               В) 3;          2. Яке з поданих нерівностей не має розв’язків?	Г) ;3
А)  cosx1                  Б) cosx1                  В) cosx1	Г) cosx1

                                                              3                  3

3.  Обчислити cos(arcsinarccos)

                                                            2                  2

3

        А)0                       Б)                    В) 1                Г) 

2

4.  Розв’язати рівняння 8^x 16

     А) 2                           Б)                 В)             Г) 4

5.  Для якої функції область визначення є множина всіх дійсних чисел?

А)  y  log₃ x                                        В) y log₃ (x² 1)

Б)  y  log₃ (x)                                  Г) y  log₃ (x² 1)

6.  Обчислити площу трикутника зі сторонами 4см і 3 2 см та кутом 45° між ними.

А)12см²                     Б)6см²                        В)12 2 см²                 Г) 6 2 см²

 

Достатній  рівень

 

1.    Побудувати графік функції  y log₂(x3)2

 

2.    Розв’язати рівняння 2sin² x 1 cosx

 

 Високий  рівень

 

1.    Розв’язати нерівність 4^x  62^x 8  0

 

2.    Висота циліндра дорівнює 8 см, радіус основи – 5 см. На відстані 4 см від осі циліндра паралельно їй проведено переріз. Знайти площу цього перерізу.

 

 

 

 

 

 

 

 

 

 

 

 

Середній рівень

 

1.    Розв’язати рівняння  cosx0



     А)     n,n Z                                      В) 2n,n Z

2

       Б)   n,nZ                                                Г)  2n,n Z

2.    Знайти координати точки перетину графіків функцій  y  lg x і  y  3

     А) (30; 3)                           Б) (10;3)                    В) (3;1000)               Г) (1000; 3)

                                                                              x                         4

                                                                          

3.    Розв’язати нерівність                     

                                                                    4      4 

А) (0;4)                  Б) (4; )             4. Розв’язати рівняння 5x  sin5

В) ( -; 4)

Г) ( -; )

       _А) ⁵ sin5              Б) log₅ sin5             _В) sin5                Г) рішень немає

5. Розв’язати нерівність log5 9  log5 x
А) (0; 9)               Б) (5; 9)                     В) (-; 9)		Г) (9; )

6. Обчислити площу бокової поверхні конуса, у якого радіус основи дорівнює 8см, а твірна – 12см.

     А) 32π                    Б) 48π                        В) 48                          Г) 96π

 

 

Достатній  рівень

 

1.    Побудувати графік функції           y x11

2.    Розв’язати рівняння 3^x 3^2x 10

 

 

Високий  рівень

 

1.      Розв’яжіть нерівність 4 ^x2 8  92 ^x2

 

2.      Паралельно осі циліндра радіус основи якого дорівнює 8 см проведена площина, яка пересікає основу циліндра по хорді, що стягує дугу 120º. Знайдіть площу перерізу, якщо діагональ дорівнює 16см.

 

 

 

 

 

 

 

 

 

 

контрольна робота з  предмету «Математика»

 

Варіант 5

 

1.   Порівняйте  3³ 2   і   ³ 52

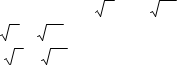
А) 3³ 2  ³ 52                           В) 3³ 2  ³ 52 Б)  3³ 2  ³ 52                            Г) порівняти неможливо

x

                                                               1       1

2.   Розв’язати нерівність             

                                                               2     16

А) [8; )                     Б) [4; )                     В) (-; 8]         3. Знайти значення виразу  log4(64a), якщо  log4 a 2	Г) (-; 4]
А) 128                        Б) 5                            В) 66                4. Спростити вираз  2sin2 cos2	Г) 7
А) -1                           Б) 1                             В) 4sin2 1 5. Яка з функцій спадає на проміжку (0; )	Г) sin2
9 А) y  9x                     Б) y                    В) y  9x           x	Г) y  log9 x

6. Обчислити об’єм конуса, висота якого дорівнює 6см, а радіус основи – 5см.

А) 50π                        Б) 150π                      В) 30π                        Г)  10π

 

 

Достатній  рівень

 

1.    Розв’язати рівняння  49^x  67^x  7  0

 

2.    Розв’язати рівняння sin2xcos2x10

 

 

Високий  рівень

 

1.    Розв’яжіть нерівність  sinxcosx

 

2.    Точка А знаходиться на відстані 9 см від площини α. Похилі АВ і АС утворюють з площиною α кути 45º і 60º, а кут між проекціями похилих на площину α дорівнює 150º. Знайдіть відстань між точками В і С.

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                   10                            9

                                        7         7 

1.  Порівняти           та          13       13

                        10                          9                                                                             10                          9

А)  7    7                          В)  7     7 

            13      13                               13      13

Б) ^ 7 ^¹⁰  ^ 7 ^⁹                                   Г) порівняти неможливо

            13      13

2.  Обчислити  log_0,25 (1 cos^)

3

        А)                       Б) 1                В)-1                            Г) -2

3.  Розв’язати нерівність log_0,2 x  log_0,2 6

         А) (0; 6)             Б) (-; 6)                   В) (6; )                      Г) (-;)

 

4.  Знайти координати точок перетину графіку функції y  log₂ (x² 3x 8)з віссю ординат

      А) (0; 3)                 Б) (0; 8)                     В) (3; 0)                     Г) (8; 0)

 

5.  Знайти множину значень функції  yx4² 6

      А) [4;)                   Б) (;4)                   В) (;6]                 Г) [6;)

 

6.  Обчислити об’єм циліндра, висота якого дорівнює 6см, а діаметр основи – 4см.

     А) 24π                    Б) 8π              В) 4π              Г) 12π

 

             Достатній  рівень

 

1.  Знайти область визначення функції:

5 4x  x² y 

x  2

2.  Розв’язати рівняння

7x  2x2  57x1  2x1

 

Високий  рівень

3^

1.    Розв’язати рівняння  sin3x  cos(3x)  cos(   3x) 1

2

 

 

2.    Із т. М до площини α проведені похилі МВ і МС, які утворюють з площиною кути по 30º. Знайдіть відстань від т.М до площини α, якщо ВМС=90º, а довжина відрізка ВС дорівнює 8см.

 

 

 

з  предмету «Математика»

 

Варіант 7

 

x

1. Розв’язати нерівність  5 5

                                                                      8     8

А) [1;)                  Б) (;1] 2. Обчислити  log     9

В) [1;)

Г) (;1]

₃

      А) 2                        Б) -2                           В)4                  Г)

x                       x                       2 3.  Розв’язати рівняння  1 64   5                                                               4   25      4       А) 2            Б) 1                В) -1               Г) -2   4.  Розв’язати нерівність lg(x  3)  3
А) (33; )              Б) (1003; )                         В) (0;1003)     5.  Розв’яжіть рівняння sin2x1	Г) (3; 33)
А)  k,k Z       Б)   2k,k Z    В)   2k,k Z                          4                                  4                                  2	Г) 1k  k,k Z 4

6. Обчислити площу бокової поверхні конуса, у якого твірна дорівнює 8, а радіус основи – 10см.

     А) 40π                    Б) 80π                        В) 40                          Г) 80

 

Достатній  рівень

 

1.    Знайти область визначення функції:

x 5(2 x)

                      y lg(x2 1)        

2.    Розв’язати рівняння  2x1  2x2  4482x3

 

 

Високий  рівень

1.    Доведіть тотожність 1 cos2 sin2  tg

1 cos2 sin2

 

2.    Точка К знаходиться на відстані 6 см від площини α. Похилі КА і КВ утворюють з площиною α кути 45º і 30º, а кут між  похилими на площину α дорівнює 150º. Знайдіть відстань між точками А і В .

 

 

 

 

 

 

 

 

1.    Порівняти  3² та 9

      А) 3 < 9                           В)  3 ² > 9

        Б) 3 = 9                           Г)  порівняти неможливо

2.    Розв’язати нерівність  logx log6

      А) (-; 6)               Б) (0; 6)                      В) ((;6)                    Г) (6; )

3

3.    Розв’язати рівняння  cos2x 

2

   А) 1ⁿ ^ ^n ,n Z                          В) ^ 2n,n Z

                            6      2                                                  6

     Б)   ^ n,n Z                             Г) 1ⁿ  ^ n,n Z

                    12                                                                    12

4.    Розв’язати нерівність 3^x  9

        А) 1                      Б) 1,5             В)0,2              Г)2,4

 

5

5.    Обчислити 3log₅                      log₅ 27

3

      А) 125                   Б) 5                В) 3                Г) 2

 

6.    Обчислити площу бокової поверхні прямої призми, у якої основою є ромб зі стороною 9см, а бічне ребро дорівнює 5см.

      А) 180                   Б) 360                        В) 405                        Г) 90

 

 

Достатній  рівень

 

1.     Розв’язати рівняння  3^2x2  9^x  270

2.     Розв’язати рівняння 6sin2 x 3sinxcosx 5cos2 x  2

 

Високий  рівень

 

1.    Розв’яжіть рівняння 53x2 32x1  9 33x 52x

5

 

2.    Знайти об’єм правильної  чотирикутної піраміди, у якої сторона основи дорівнює 6см, а діагональний переріз є прямокутний трикутник.

 

 

 

 

 

 

 

1.    Розв’язати нерівність  0,6^x  0,36

        А) (-; 0,6]                      Б) [0,6; )                 В) (-; 2]                   Г) [2; )

log⁵ 3

2.    Обчислити  log₂

log₅ 9

А) -1

Б) 1

1      В) log2     3

1       Г) log2       6

3^

3.    Спростити вираз ctg(2)ctg(          )

2

          А) ctg²                       Б) tg²                      В) 1                Г) -1

4.    Яке з поданих чисел являється розв’язком нерівності sin(3x ^)  1 ?

                                                                                                                                                                         6       2

       А) 0                      Б) ^                         В) ^                       Г) ^

                                                       6                                  3                                 2

5.    Розв’язати нерівність log₃(x  2)  2

          А) (2; 11)                    Б) (2; 10)                   В) (-; 11)                 Г) (-; 7)

 

6.    Кут між твірною МА та площиною основи конуса дорівнює 30º, радіус основи           дорівнює 6 3 см. Знайти висоту конуса.

 

 

Достатній  рівень

 

    1.  Розв’язати рівняння  22x1  3 2x  2  0

 

sin2x

    2 . Розв’язати рівняння    2sin x

1 cosx

 

Високий  рівень

1.    Розв’язати рівняння  log₅ (2x² 3x1)  log₅ (2x 2)

 

2.    Із точки А на площину  проведено дві похилих AB=AC=6 см. Кут між ними дорівнює 60º, а між їхніми проекціями - 90º. Знайти відстань від точки А до площини.

 

 

 

 

 

 

 

 

 

 

 

 

1. Розв’язати рівняння               log₅ x  2

А)                           Б) 25                          В) -10                         Г) 

6 2. Знайти область визначення функції f (x)  5 x  6
А) 6;               Б) 6;                В) ;66;		Г) ;

 

3.  Розв’яжіть рівняння 2^x2  2^x 10

А) 1                Б) 2                В) 3                Г) 4

 

4.  Розв’язати рівняння  2sinxcosx 2

А) 1ⁿ  ¹ arcsin 2 ^n ,n Z                       В)  1ⁿ ^n,n Z

                       2                     2                                                           4

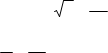Б) 1ⁿ ^ ^n ,n Z                                          Г) коренів нема

                       8      2

5.  Вибрати функцію, у якої область визначення складається з однієї точки

                  1                                  ⁴ x²                  В) y ⁴ x²                    Г) y ⁴ x

А) y  x₂                       Б) y 

6.  Сторона основи правильної трикутної піраміди дорівнює 6см, а висота піраміди - 5 3 см. Обчислити об’єм піраміди.

А) 30 3                        Б) 90 3                      В) 45              Г) 135

 

Достатній  рівень

 

1.    Знайти область визначення функції:

y  log0,6 x  2 x 3

2.    Розв’язати рівняння  3^x 5^x2  0.0415^83x

 

Високий  рівень

 

1.   Розв’яжіть нерівність log₃ log₁ log₁ x 0

                                                                                   2              3

 

2.   Основою піраміди служить прямокутник зі сторонами 18 і 24. Кожне з бічних ребер

дорівнює 25. Знайти об'єм піраміди.

 

 

 

 

 

 

 

 

1.    Знайти корінь рівняння  0,4^x  0,064

        А) 1,6                   Б) 0,16                       В) 3                Г) 4

2.    Графіку  якої з поданих функцій належить точка В(-81; -3)?

          А) y ⁴ x                            Б) y ⁴ x                   В) y⁴ x                   Г) y ⁴  x

3.    Розв’язати нерівність        log(3x)  log5

        А) (-; -2)                        Б) (-2; )                   В) (-2; 3)                    Г) (2;3)

4.    Яка з поданих нерівностей не має рішень?

         А) arcsinx 0                              В)  sin x _ ^

2

        Б) arcsinx  0                             Г)  sin x _ ^

2

5.    Обчислити   

        А) 2          Б) 5                В) 10              Г)20

.

6.    Пряма m паралельна стороні FK трикутника DFK. Яке взаємне розташування прямих m і  DK , якщо пряма m не належить площині DFK?

        А) паралельні                                       В) встановити неможливо

        Б) перехресні                                      Г) перетинаються

 

 

Достатній  рівень

 

1.      Знайти область визначення функції:

²)           1 y  lg(6x  x lg(3 x)

2.      Розв’язати рівняння  22x1  3 2x  2  0

 

 

Високий  рівень

 

1.    Розв’язати рівняння  sin² x 4sinxcosx3cos² x 0

 

2.    В кулю вписаний циліндр, у якого радіус основи дорівнює r , а висота дорівнює 4r. Знайти площу поверхні кулі.

 

 

 

 

 

 

 

 

 

 

 

Підсумкова контрольна робота  з  предмету «Математика»

 

Варіант 12

 

Середній рівень

1. Знайти корінь рівняння 4x  8
А) 3                      Б) 2,5                         В) 2      2. Спростити вираз  sin()  sincos	Г)1,5
А) cossin                       Б) coscos               3. Обчислити  log5 81log3 5	В) sincos	Г) sinsin

        А) 4                          Б)                         В) 3                Г)27

4. Розв’язати нерівність 3x  1 3
А) 1;         Б) 1;               В) ;1   5. Яке з поданих рівнянь не має рішень? А) arcsinx 1                            В) arccosx   6 Б) sinx 1                                 Г) cosx   6		Г) ;1

6. Ребро куба збільшили в 2 рази. В скільки разів збільшився об’єм куба?

        А) в 16 разів                  В) в 4 рази

        Б) в 8 разів                     Г) в 2 рази

 

 

Достатній  рівень

1.    Знайти область визначення функції:

²)           1 y  lg(9x  x lg(5 x)

2.    Розв’язати рівняння sin x  cosx²   

 

 

Високий  рівень

 

1.   Розв’язати нерівність lg²100x 5lgx  6

 

2.   У основі призми лежить рівносторонній трикутник, площа якого дорівнює 9 3 . Знайти об'єм призми, якщо її висота в 3 раз більше сторони основи.

 

 

 

 

 

 

 

Середній рівень

x

1.      Розв’язати рівняння  ^3^  5

                                                                  5      3

     А) -1                       Б) 1                В)0                             Г) рішень немає

2.      Яке з поданих рівностей вірно?

      А) log₃        3  2                               В) log     3   

      Б) log₃            3                               Г) log    3  1

3.      Розв’язати рівняння:  12sin² 2x 2

      А)  1 arccos 2 ^n ;n Z                               _В) ^n ;n Z

                  4                      2                                                   4



      Б)    2n;n Z                                              Г) рішень немає

4

4.      Який з поданих виразів має тільки від’ємне значення?

         А) x⁶  6                           Б)  x⁶  6                  В)  x⁶  6                 Г)  (x  6)⁶

5.      Розв’язати нерівність 3^x2 1

   А) ;2                       Б) ;3               В) 2;                 Г) 3;

 

6.      Обчислити об’єм кулі с радіусом 3 см.

     А) 36π                    Б) 9π                          В) 108π                      Г) 54π

 

 

Достатній  рівень

 

1.   Розв’язати рівняння  log6(x2)log6(x1) 1

2.   Розв’язати рівняння log₂ x  2log_x 2  3

 

Високий  рівень

1.    Доведіть тотожність 11^cossin22^ 1 tg2₂ 1

 

2.    Вершини квадрата із стороною 12 2 см лежать на поверхні кулі, а відстань від центра кулі до площини квадрата дорівнює 16см. Знайти об’єм кулі.

 

 

 

 

 

 

 

 

 

x

1.    Знайти корені рівняння sin  1

2



      А)   2n;n Z                                    В)  4n;n Z

2



      Б)  n;n Z                                       Г)  4n;nZ

4

x

2.    Розв’язати нерівність  ^1^  1

                                                                   3      27

   А) ;3           Б) 3;                 В) ;3            Г) 3;

3.    Обчислити cos2, якщо sin²   

         А)                        Б)               В)                          Г)  

4.    Яке з поданих рівнянь не має рішень?

      А) cos x                       Б) cosx  ^                    В) cosx   ⁵            Г) cosx  _    ³

                                                                                           6                                             6                                   2

1

5.    Знайти область визначення функції  f (x) 

log₅ x 1

А) 0;55;           Б) 5;                 В) 0;5                  Г) 0;

 

6.    Знайти відношення об’ємів двох куль, радіуси яких дорівнюють 3см та 6см.

     А) 1:3                     Б) 1:8                         В) 1:2                         Г)1:4

 

 

Достатній  рівень

 

    1. Обчислити   (log₁₄ 2log₁₄ 7 5^{log5 6} )^{log7 2}     2.  Побудувати графік функції

              y  cos^_^x_1

 2

 

Високий  рівень

 

1.    Розв’яжіть рівняння sin² x 3sinx cosx 0

 

2.    Сторони основи трикутної піраміди  рівні 6 см, 6 см і 8 см, бічні ребра рівні й довжина кожного 9 см. Знайти висоту піраміди. 

 

 

 

 

 

                                                                        1            ²      

                Спростити вираз       cos₂  tg 

        А) 1                      Б) -1                В) sin²                      Г) cos²

2.  Розв’язати нерівність   log₃ (x  2) 1

     А) ;1         Б) 1;      В) 3;                 Г) 0;

3.  Яке найменше значення може приймати функція f (x)  2sin3x  2

        А) -1                     Б) -8               В) 0                Г) -4

4.  Спростіть вираз

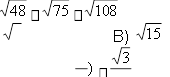          А) 2 3                   Б) 3 3                                                Г)     3

5.  Розв’язати рівняння  tg(x ^

                                                                                  4        3

                                                                   5^

        А)   n;n Z                                     _В)  n;n Z

                 12                                                            12

                                                                    7^

        Б)  n;n Z                                   _Г)  n;n Z

                    12                                                          12

6.  Точка М віддалена від площини  α на 15см. З цієї точки проведена до площини α похила МК. Знайти довжину цієї похилої, якщо її проекція на площину α дорівнює 8 см.

        А) 16                    Б) 17              В) 19              Г) 23

 

 

Достатній  рівень

 

1.     Розв’язати нерівність 2log_0.4 (x)  log_0.4 (109x)

 

2.     Розв’язати рівняння log₂ x  2log_x 2  3

 

 

 

Високий  рівень

 

1.     Побудувати графік функції

y  x2 x2

 

2.     Висота правильної трикутної піраміди дорівнює 15 см, а апофема – 17см. Обчислити 

площу повної поверхні піраміди.

 

 

 

 

 

 

 

3

Обчислити значення виразу sin(arccos)

2

                                                                                              3                              3

        А)                       Б)                    В)                             Г) 

                                                                                             2                              2

2.  Розв’язати рівняння log_0,2 (2x3)  1

        А) 2,5                   Б) 4                В) 1                            Г) 1,4

x

                                                                    11       4

3.  Розв’язати нерівність        

                                                                     4       11

А) ;1                Б) 1;               В) ;1 1 4. Знайти область визначення функції y    lg(x1)	Г) 1;
А) 0;         Б) 1;             В) 0;11; 5. Розв’язати нерівність log3(x  2)  2	Г) 1;00;
А) (2; 11)             Б) (2; 10)                   В) (-; 11)	Г) (-; 7)

6. Радіус основи конуса дорівнює 12см, а кут при вершині осьового перерізу - 120º.

Знайти твірну конуса.

          А) 6 3                   Б) 8 3                        В) 6                Г) 24

 

 

Достатній  рівень

 

1.     Побудувати графік функції

4

y    2 x  2

2.     Розв’язати рівняння x^lgx3 10000

 

 

 

Високий  рівень     1.  Розв’яжіть рівняння 53x2 32x1  9 33x 52x

5

 

2. Довжини окружностей основ усіченого конуса рівні 4 і 10. Висота конуса дорівнює 4. Знайти площу поверхні усіченого конуса.

 

 

 .   

 

 

 

Встановити, при якому значенні х виповнюється рівність 3^x  9

        А) 1                      Б) 2                В) 4                Г) 9

2.  Спростити вираз 1 cos²  sin² 

          А) 2sin²                          Б) 2cos²                  В) 0                Г) 2

5

3.  Обчислити 3log₅                 log₅ 27

3

        А) 125                 Б) 5                В) 3                Г) 2

 

4.  Серед поданих функцій вкажіть непарну функцію

          А) y  xcosx                                В) y      cosx

1

            Б) yxcosx                              Г)  y 

cosx

5.  Розв’язати рівняння  log₂ (x²  3x)  2

        А) -1; 4                Б) -4;1                       В) 4                Г) 1

 

6.  Знайти площу бокової поверхні правильної восьмикутної піраміди, у якої сторона основи дорівнює 6см, а апофема – 16см.

 

Достатній  рівень

1 lg253lg2

1.    Обчислити   1000²  

 

2.    Розв’язати рівняння 6sin2 x 3sinxcosx 5cos2 x  2

 

 

Високий  рівень

 

 

1.    Доведіть тотожність 1 cos2 sin2  tg

1 cos2 sin2

 

2.    Основа піраміди – квадрат із стороною 12см, а дві суміжні бокові грані перпендикулярні до площини основи. Обчислити площу бокової поверхні піраміди, якщо її висота дорівнює 5 см.

 

 

 

 

 

 

 

 

 

 

 

 

Середній рівень

 

1.  Знайти значення виразу   log₅ 50 log₅ 2

А) log₅ 48                    Б) 2                В) 5                Г) 20

2.  Яка з поданих функцій являється непарною?

А) y  5x                                 Б) y  5x  2               В) y  5x²  2                      Г) y _ x⁵₂

3.  Яке з поданих нерівностей не має рішень?

А) ⁴ x4 0             Б) ⁴ x⁴  0                   В) ⁴ x  0                 Г) ⁴ x⁴ 0

 

4.  Серед поданих функцій вкажіть пару функцій, які не являються взаємно зворотними

А) y  9^x та y  log₉ x                                    В) y tgx та y ctgx

Б) y  9x та y   x                                        Г) y  x³ та y ³ x

5.  Розв’язати рівняння  lglog₃ log₂ x  0

А) 8                Б) 9                В) 2                Г) 3

 

6.  Об’єм циліндра дорівнює 12см³. Чому буде дорівнювати його об’єм, якщо радіус основи збільшити в 2 рази?

А) 24              Б) 36              В) 42              Г) 48

 

 

Достатній  рівень

 

1.    Побудувати графік функції

y  sin(x ^)

3

2.    Розв’язати рівняння  lg(x  2)  lg5  lg(x  6)

 

 

Високий  рівень

 

1.    Розв’яжіть нерівність  sinxcosx

 

 

2.    Сторона основи правильної трикутної піраміди дорівнює 8 см, а бічна грань нахилена до лощини основи під кутом 30º. Знайти площу повної поверхні піраміди.

 

 

 

 

 

 

 

 

1. Коренем якого з поданих рівнянь є число 3?

         А) log_x 9  3                       Б) log₉ x              В) log_x 27  3                        Г) log₃ x  9

2. Знайти область визначення функції y  4 x16
А) 16;                Б) 16;               В) 2;   3. Розв’язати нерівність  0,1x5 10	Г) 2;
А) ;4       Б) 4;                 В) ;6    4. Розв’язати нерівність log0,2 x log0,2 6	Г) 6;
А) (0; 6)               Б) (-; 6)                   В) (6; )	Г) (-;)

 

5.  Знайти область визначення функції f (x)  x41 x

   А) ;14;                В) 4;

     Б) ;1                             Г) 1;4

 

6.  Усередині кулі з центром О проведено переріз з центром О₁ на відстані 5 см від центра кулі. Знайти радіус перерізу , якщо радіус кулі дорівнює 13см.

        А) 4                      Б) 6                В) 12              Г) 10

 

 

 

Достатній  рівень

 

1.     Побудувати графік функції

                y  cos(x ^)

4

2.     Розв’язати рівняння  lg(x  4)  lg(x  5) 1

 

 

Високий  рівень

 

 

1.  Розв’яжіть нерівність 4 ^x2 8  92 ^x2

 

2.  Висота правильної чотирикутної піраміди дорівнює 12 см, а апофема – 15см. Обчислити площу повної поверхні піраміди.

 

 

 

 

 

 

 

з  предмету «Математика»

 

Варіант 20

 

Середній рівень

                                                                                                                                                       7             6

1.    Порівняйте основу логарифму з одиницею, якщо log_a                    log_a                    

                                                                                                                                                       9            11

        А) a>1                 Б) a=1                        В) a<1                       Г) порівняти неможливо

                                                                                  x          2

2.    Знайти корені рівняння sin                 

                                                                                 4         2

        А) 1ⁿ _ ^ _^n ;n Z                        В) 1ⁿ  4n;nZ

                              16     4

Б) 1^n1 _ ^  4n;n Z               Г)  1^n1  4n;nZ 16

3.    Знайдіть cos, якщо sin 0,6 і  ^

2

        А)    0,4             Б) 0,8              В) -0,8              Г) інша відповідь 

 

4.    Розв’язати рівняння 5^xx2  7^xx2

        А) 0                      Б) -1; 0                      В) 0; 1            Г) рішень нема

5.    Яка з поданих функцій зростає на проміжку 0;?

x

                         1                            1                                ^1                   Г) y logx

         А) y      x            Б) y                         В) y _{   }

                         3                            3x                               3                                

6.    Точка М знаходиться поза площиною трикутника АВС. Яке взаємне розташування прямих ВС та МА?

        А) встановити неможливо                             В) перетинаються

        Б) паралельні                                                   Г) перехресні

 

 

Достатній  рівень

1.   Розв’язати рівняння log₅² x  0.5log₅ x²  6

 

2.   Розв’язати рівняння 2sin² x 1 cosx

 

Високий  рівень

 

1 lg² 5       1. Обчисліть значення виразу   lg5.

2lg 10  lg5

 

2. Сторона основи правильної чотирикутної піраміди дорівнює 4 см, а бічна грань   нахилена до площини основи під кутом 60 º. Знайти площу повної поверхні піраміди.

 

 

 

 

 

1.    Знайти значення виразу tg(arcsin)ctg(arcsin)

           А)                         Б)                 В)             Г) 1

2.    Знайти корені рівняння cos(3x ^) 1

2

                  2n                                                     2^n

        А)              ;n Z                                    В)   ;n Z

                6       3                                                        3

         Б)   2n ;n Z                                 _Г) ^  ^2n ;n Z

                    6       3                                                   3       3

3.    Скільки коренів має рівняння cosx log₂ 3?

        А) жодного         Б) 1                В) 2                Г) безліч багато 

 

4.    Яке з рівнянь є рівнянням прямої?

        А) 2x  y  5            Б) 2x²  y  5                 В) 2x²  2y²  8                 Г) x  y³  8

 

5.    Розв’язати нерівність 6^{log6x9}  3

      А) 9;             Б) (9; 12)                 В) ;12             Г) 12;

 

6.    Обчислити об’єм конуса, у якого діаметр основи дорівнює 12см, а висота – 5см.

        А) 60π                  Б) 20π                        В) 10π                        Г) 30π

 

 

Достатній  рівень

 

1.               Побудувати графік функції               y  cos^_^x_1

 2

2.               Розв’язати рівняння  log₃² x  log₃ x²  2

 

Високий  рівень

 

1.  Обчисліть значення виразу  a 96 a36 a  при  a 8

³ a 3⁶ a

 

2.  В куб вписана куля. Обчислити відсоткове відношення об’єму кулі до об’єму куба.