Підсумкова контрольна робота з математики у форматі ЗНО для учніх 10 класів, які вивчають математику на стандартному рівні.
|
Зошит 1 |
ПІДСУМКОВА КОНТРОЛЬНА РОБОТА
(за 10 клас)
З МАТЕМАТИКИ
(ЗАВДАННЯ РІВНЯ СТАНДАРТУ)
Час виконання – 90 хвилин
Робота складається з 18 завдань різних форм. Відповіді до завдань 1–16 Ви маєте позначити в бланку А. Розв’язання завдань 17, 18 Ви маєте записати в бланку Б.
Результат виконання всіх завдань буде зараховано як результат підсумкової контрольної роботи з алгебри та геометрії, які вивчали математику на рівні стандарту.
Інструкція щодо роботи в зошиті
1. Правила виконання завдань зазначено перед кожною новою формою завдань.
2. Рисунки до завдань виконано схематично, без строгого дотримання пропорцій.
3. Відповідайте лише після того, як Ви уважно прочитали та зрозуміли завдання. Використовуйте як чернетку вільні від тексту місця в зошиті.
4. Намагайтеся виконати всі завдання.
5. Ви можете скористатися довідковими матеріалами, для зручності Ви можете їх відокремити відірвавши.
Інструкція щодо заповнення бланків відповідей А та Б
1. У бланк А записуйте чітко, згідно з вимогами інструкції до кожної форми завдань, лише правильні, на Вашу думку, відповіді.
2. Неправильно позначені, підчищені відповіді в бланку А буде зарахо- вано як помилкові.
3. Якщо Ви позначили відповідь до якогось із завдань 1–16 у бланку А неправильно, то можете виправити її, замалювавши попередню позначку та поставивши нову, як показано на зразках:
4. Якщо Ви записали відповідь до якогось із завдань 11–12 неправильно, то можете виправити її, записавши новий варіант відповіді в спеціально відведених місцях бланка А.
5. Виконавши завдання 17 та 18 у зошиті, акуратно запишіть їхні розв’язання в бланку Б.
6. Ваш результат залежатиме від загальної кількості правильних відповідей, записаних у бланку А, та правильного розв’язання завдань 17, 18 у бланку Б.
 Ознайомившись з інструкціями, перевірте якість друку зошита та кількість сторінок. Їх має бути . Позначте номер Вашого зошита у відповідному місці бланка А так:
Ознайомившись з інструкціями, перевірте якість друку зошита та кількість сторінок. Їх має бути . Позначте номер Вашого зошита у відповідному місці бланка А так:
Зичимо Вам успіху!
ДОВІДКОВІ МАТЕРІАЛИ
Таблиця квадратів від 10 до 49
|
Десятки |
|
|
|
|
Одиниці |
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
1 |
100 |
121 |
144 |
169 |
196 |
225 |
256 |
289 |
324 |
361 |
|
2 |
400 |
441 |
484 |
529 |
576 |
625 |
676 |
729 |
784 |
841 |
|
3 |
900 |
961 |
1024 |
1089 |
1156 |
1225 |
1296 |
1369 |
1444 |
1521 |
|
4 |
1600 |
1681 |
1764 |
1849 |
1936 |
2025 |
2116 |
2209 |
2304 |
2401 |
АЛГЕБРА І ПОЧАТКИ АНАЛІЗУ
Формули скороченого множення Квадратне рівняння
|
a2 – b2 = (a – b)(a + b) (a + b)2 = a2 + 2ab + b2 (a – b)2 = a2 – 2ab + b2 |
ax2 + bx + c = 0, a ≠ 0 = b2 – 4ac – дискримінант
x1 = —2a , x2 = 2a –b |
Модуль числа x1 = x2 = 2—а , якщо D = 0
![]() a =
a = ![]() a–a, якщо , якщо а а < 0, 0 ax2 + bx + c = a(x – x1)(x – x2)
a–a, якщо , якщо а а < 0, 0 ax2 + bx + c = a(x – x1)(x – x2)
|
тепені |
|
Логарифми |
|
a1 = а, аn = a ⋅ a ... ⋅ a для a ∈ R, n ∈ N, n n разів
1 a–n = —аn для а ≠ 0, n ∈ N m |
a > 0, а ≠ 1, b > 0, c > 0, k ≠ 0 alogab = b logаа = 1 logа1 = 0 logа(b ⋅ c) = logаb + logаc |
![]() a—n = n am, а >0, m ∈ Z, n ∈ N, n
a—n = n am, а >0, m ∈ Z, n ∈ N, n ![]() 2 logа b–c = logаb – logаc
2 logа b–c = logаb – logаc
|
ax ⋅ ay = ax + y |
аx —y = ax – y а |
(ax)y = ax ⋅ y |
logаbn = n ⋅ logаb |
(ab)x = ax ⋅ bx (a–b)x = —аbxx logаkb = ![]() аb
аb
|
Арифметична прогресія |
|
Геометрична прогресія |
an = a1 + d(n – 1) Sn= —1 + 2 аn ⋅ n bn = b1 ⋅ qn – 1 Sn = b—1q (q– 1n– 1), (q ≠ 1) a
|
Теорія ймовірностей |
|
Комбінаторика |
P(A) = k–n Pn = 1 ⋅ 2 ⋅ 3 ⋅ ... ⋅ n = n! Cnk = k—! ⋅ (nn – ! k)! Ank = —(n – n!k)!
Завдання 1–4 і 5–16 мають відповідно по чотири та п’ять варіантів відповіді, з яких лише один правильний. Виберіть правильний, на Вашу думку, варіант відповіді, позначте його в бланку А згідно з інструкцією. Не робіть інших позначок у бланку А, тому що результат не буде зарахований!
Будьте особливо уважні під час заповнення бланка А!
Не погіршуйте власноручно свого результату неправильною формою запису відповідей
8.
 9.
9.
10.
У завданнях 11–12 до кожного з трьох рядків інформації, позначених цифрами, доберіть один правильний, на Вашу думку, варіант, позначений буквою. Поставте позначки в таблицях відповідей до завдань у бланку А на перетині відповідних рядків (цифри) і колонок (букви). Усі інші види Вашого запису в бланку А будуть зараховані, як помилки!
Будьте особливо уважні під час заповнення бланка А!
Не погіршуйте власноручно свого результату неправильною формою запису відповідей
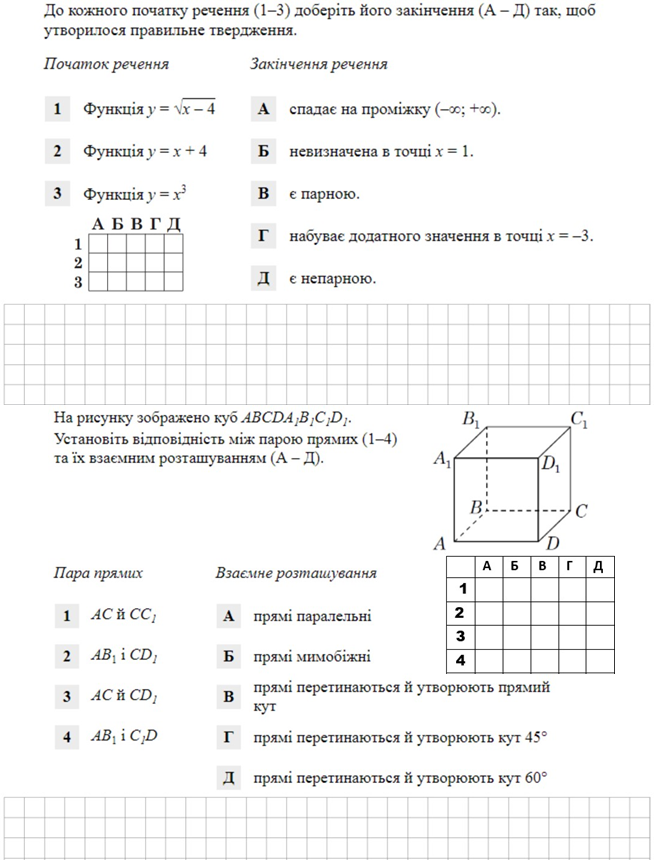 11.
11.
12.
Розв’яжіть завдання 13–16. Одержані числові відповіді запишіть у зошиті та бланку А. Відповідь записуйте лише десятковим дробом, урахувавши положення коми, по одній цифрі в кожній клітинці відповідно до зразків, наведених у бланку А.
 13.
13.
14.
15.
 16.
16.
Розв’яжіть завдання 17, 18. Запишіть у бланку Б послідовні логічні дії та пояснення всіх етапів розв’язання завдань, зробіть посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання завдань рисунками, графіками тощо.


Похідна функції Первісна функції
та визначений інтеграл
, – сталі
|
|
Загальний вигляд |
|
Функція f(x) |
первісних F(x) + C, C – довільна стала |
|
0 |
C |
|
1 |
x + C |
|
x, ≠ –1 |
—x + 1 + C + 1 |
|
1–x |
ln x + C |
|
ex |
ex + C |
|
sin x |
–cos x + C |
|
cos x |
sin x + C |
|
1 —2 x cos |
tg x + C |
( )′ = 0
х′ = 1 (х)′ = x–1
![]() ( x)′ = –21x (ex)′ = ex
( x)′ = –21x (ex)′ = ex
(ln x)′ = 1–x (sin x)′ = cos x
(cos x)′ = –sin x (tg x)′ = cos–12x
(u + v)′ = u′ + v′ (u – v)′ = u′ – v′
(uv)′ = u′v + uv′ (Cu)′ = Cu′
(u–v)′ = u–′v – v2uv′
∫bf(x)dx = F(x)ab = F(b) – F(a) – формула Ньютона-Лейбніца
a
Тригонометрія
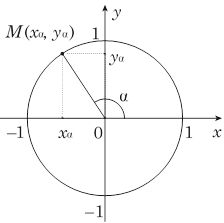 sin = y cos = x sin2 + cos2 = 1 tg = –cossin 1 + tg2 = cos–12 sin2 = 2sin cos cos2 = cos2 – sin2 sin(90o + ) = cos sin(180o – ) = sin cos(90o + ) = –sin cos(180o – ) = –cos tg(90o + ) = – –tg1 tg(180o – ) = –tg
sin = y cos = x sin2 + cos2 = 1 tg = –cossin 1 + tg2 = cos–12 sin2 = 2sin cos cos2 = cos2 – sin2 sin(90o + ) = cos sin(180o – ) = sin cos(90o + ) = –sin cos(180o – ) = –cos tg(90o + ) = – –tg1 tg(180o – ) = –tg
Таблиця значень тригонометричних функцій деяких кутів
|
α |
рад |
0 |
–π 6 |
–π 4 |
–π 3 |
–π 2 |
π |
3—π 2 |
2π |
|
град |
0o |
30o |
45o |
60o |
90o |
180o |
270o |
360o |
|
|
|
sin α |
0 |
1– 2 |
|
|
1 |
0 |
–1 |
0 |
|
|
cos α |
1 |
|
|
1– 2 |
0 |
–1 |
0 |
1 |
|
|
tg α |
0 |
|
1 |
|
не існує |
0 |
не існує |
0 |
19
ГЕОМЕТРІЯ
![]()
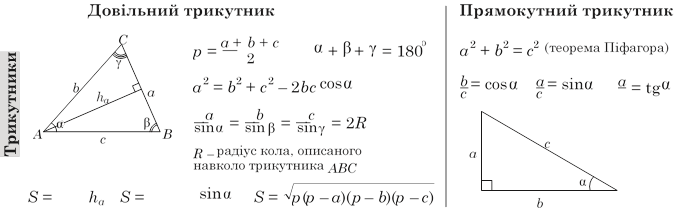 b
b
 Паралелограм Прямокутник Ромб Трапеція
Паралелограм Прямокутник Ромб Трапеція
b
a
S= ab
L = 2πR
(x – x0)2 + (y – y0)2 = R2
Правильна піраміда
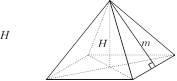
V =
1–3 Sосн ⋅ H
1– Pосн ⋅ m Sб = 2
Координати та вектори
M(x0, y0, z0)
![]()
A(x1, y1, z1) B(x2, y2, z2)
![]()
 b
b
a
S = 1–2 d1d2, S = —a + b2 ⋅ h,
d1, d2 – діагоналі ромба a і b – основи трапеції
 S = πR2
S = πR2
|
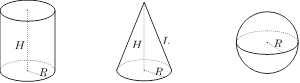
Циліндр |
Конус |
Куля, сфера |
|
V = πR2H Sб = 2πRH |
1 V = – πR2H 3 Sб = πRL |
4 V = – πR3 3 S = 4πR2 |
||||
|
|
x = —1 + x2 x |
y = —1 + y2 y |
z = —1 + z2 z |
|
||
0 2 0 2 0 2
AB(x2 – x1, y2 – y1, z2 – z1) AB= (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2

![]() a ⋅ b = a1b1 + a2b2 + a3b3 a ⋅ b = a
a ⋅ b = a1b1 + a2b2 + a3b3 a ⋅ b = a
Кінець зошита
20


про публікацію авторської розробки
Додати розробку
