Підсумкова контрольна робота за І семестр алгебра

І варіант

1.  (1б) Яка з наведених рівностей є правильною?

      а) ;                  в) ;

      б)   ;                г) .

2. (1б) Розв’яжіть нерівність: .

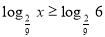     а) [6; ∞);       б) ( – ∞; 6] ;          в) (0;6];            г) (0;6)∪(6;∞)

3. (1б) Чому дорівнює значення виразу 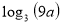, якщо ?

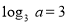    а) 6;             б) 5;                в) 27;                   г) 12.

4. (1б) Розв’язати нерівність:

                        (х + 4) ≤ 8.

5. (2б) Для функції  f(x) знайти первісну, графік якої проходить через точку М :

      а)  f(x) = 3х² – 2х + 3 , М (1 ; – 3) ;

6.  (2б) Обчислити інтеграли:

      а) ;          б) .

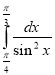7. (2б) Знайти загальний вигляд первісної для функції:

   а) f(x) = 4 + 3х² – 6 х ;     б) f(x) = 3х + cos 2х .

8. (2 б) Знайти площу фігури, обмеженою графіками функцій:

    а)   у = х² ; у = 0; х = 2;

    б)   у = 4 – х² ;   у = 2 – х ;

ІІ варіант

1. (1б) Яка з наведених рівностей є правильною?

 а) ;                  в) ;

б)   ;                г) .

2. (1б) Розв’яжіть нерівність: .

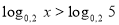 а) ( – ∞;5) ;         б) (5; ∞);         в) (0;5) ∪(5; ∞);            г) (0;5).

3. (1б) Чому дорівнює значення виразу 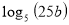, якщо ?

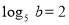    а) 4;             б) 10;                в) 7;                   г) 5.

4. (1б) Розв’язати нерівність:

                            (х – 5) ≥ 11.

5. (2б) Для функції  f(x) знайти первісну, графік якої проходить через точку М :

  а) f(x) = 4х³ + 8х – 2,  М(1; 3);

6.  (2б) Обчислити інтеграли:

  а) ;           б) .

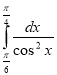7. (2б) Знайти загальний вигляд первісної для функції:

  а) f(x) = 2 – 3х² + 2х ;     б) f(x) = 4 + sin 3х .

8. (2 б) Знайти площу фігури, обмеженою графіками функцій:

       а)  у = х² ; у = 0; х = 1;

       б)  у = 5 – х² ;  у = 3 – х ;