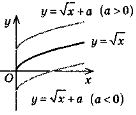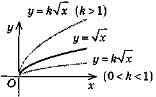Найпростіші перетворення графіків функцій.
Тема уроку. Найпростіші перетворення графіків функцій.
Мета уроку: сформувати розуміння учнями змісту поняття «перетворення графіка функції», а також розуміння того факту, що певне перетворення рівняння функції тягне за собою перетворення графіка та навпаки. Сформувати знання учнів про основні види геометричних перетворень графіків функцій (на інтуїтивному рівні) та про рівняння функції, що задається цим перетворенням. Сформувати первинні уміння «читати» графіки функцій (тобто за готовими графіками задавати рівняння функцій), а також виконувати побудови графіків функцій за допомогою перетворень, заданих рівнянням даної функції.
Тип уроку: формування знань і первинних умінь.
Наочність та обладнання: опорний конспект № 14, роздавальний матеріал (картки з розв'язаннями домашніх вправ).
Хід уроку
I. Організаційний етап
Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.
II. Перевірка домашнього завдання
Для економії часу на уроці в разі необхідності вчитель може запропонувати учням роздавальний матеріал — розв'язання домашніх вправ — самостійно опрацювати вдома.
Для організації поточного контролю за засвоєнням учнями знань та вмінь можна запропонувати їм тестові завдання (див. нижче), перевірка яких проводиться одразу після виконання. Учитель фіксує прізвища тих учнів, які потребують додаткової педагогічної уваги для можливості здійснення певної корекційної роботи.
Тестові завдання
- На рисунку зображений графік функції, область визначення якої D(f) = R. Правильним є твердження:
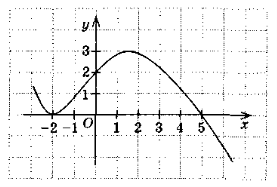
а) нулі функції: 2; 2,5; f(x) зростає, якщо х ![]() [-2; 3]; f(x) < 0, якщо
[-2; 3]; f(x) < 0, якщо
x ![]() (5; +∞);
(5; +∞);
б) нулі функції: 2; 5; f(x) зростає, якщо x ![]() [-2; 2]; f(x) < 0, якщо
[-2; 2]; f(x) < 0, якщо
х ![]() [5; +∞);
[5; +∞);
в) нулі функції:-2; 5; проміжок зростання x ![]() [-2; 2]; f(х) < 0, якщо
[-2; 2]; f(х) < 0, якщо
х ![]() (5; +∞);
(5; +∞);
г) нулі функції: 3; проміжку зростання немає; f(x) < 0, якщо
x ![]() (-∞; -2) і x
(-∞; -2) і x ![]() (2; +∞).
(2; +∞).
-
Область визначення функції у =
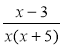 :
:
а) х ![]() 5; б) х
5; б) х ![]() -5; в) х
-5; в) х ![]() -5, х
-5, х ![]() 0; г) х
0; г) х ![]() 3.
3.
- Область значень функції f(x) = x2 – 3:
а) (-∞; +∞); б) [3; +∞); в) [-3; +∞); г) (-3; +∞).
-
Якщо f(x) = 3
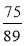 х – 1, то:
х – 1, то:
а) f (3) < f (4); б) f (3) > f (4); в) f (3) < f (4); г) f (3) = f (4).
- Значення функції у(х) = -3х + 8 додатні, якщо:
а) х ≤ 2![]() ; б) х ≥ 2
; б) х ≥ 2![]() ; в) х < 2
; в) х < 2![]() ; г) таких значень х немає.
; г) таких значень х немає.
III. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів
На цьому етапі уроку доречними будуть слова вчителя про те, що дослідження функцій за готовим графіком є більш простим, ніж за формулою (підтвердженням цієї думки можуть стати результати перевірки тестових завдань). Розвиваючи цю думку, вчитель повідомляє учням про те, що в ряді випадків для розв'язування задач необхідно буває побудувати графік функції, яка не є елементарною (учитель може навести ряд прикладів таких функцій). Отже, формулюється питання: чи існують засоби (і якщо існують, то як ними користуватися), за допомогою яких можна побудувати графік деякої функції, використовуючи при цьому вміння будувати графіки елементарних функцій (лінійної, оберненої пропорційності, квадратичної функції та функції у = ![]() ). Зрозуміло, що пошук відповіді на поставлене питання і є основною дидактичною метою уроку.
). Зрозуміло, що пошук відповіді на поставлене питання і є основною дидактичною метою уроку.
IV. Актуалізація опорних знань та вмінь учнів
Усні вправи
- Яка з наведених функцій є зростаючою:
а) на області визначення; б) на проміжках (-∞; 0) і (0; +∞)?
1) у = 4х – 1; 2) у = ![]() ; 3) у = -
; 3) у = -![]() x + 1; 4) у = 3х;
x + 1; 4) у = 3х;
5) у = ![]() ; 6) у = х2; 7) у = -
; 6) у = х2; 7) у = -![]() .
.
- Графіком якої з наведених функцій є пряма, що проходить через початок координат? Поясніть свою відповідь, не виконуючи побудови:
1) у = 2х + 1; 2) у = 2х; 3) у = 2х2; 4) у = 2; 5) у = ![]() ; 6) у =
; 6) у = ![]() .
.
- На одному з рисунків зображено графік функції у = 2х. Укажіть цей рисунок.
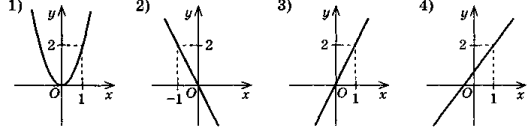
-
Для функції f(x) = x2 – 3 знайдіть значення виразу:
1) f (-2); 2) f (-1); 3) f (0); 4) f (1); 5) f (2); 6) f (3);
7) f (4); 8) f (5); 9) f (6).
V. Формування знань
План вивчення нового матеріалу
- Уявлення про перетворення графіка функції.
- Побудова графіків паралельним перенесенням вздовж осі ординат (абсцис).
- Побудова графіка функції симетрією відносно осі абсцис.
- Розтягнення (стиснення) графіка функції вздовж осі ординат.
Опорний конспект №14
|
|
Найпростіші перетворення графіків функцій |
|
|||
|
|
№ з/п |
Формула залежності |
Приклад |
Перетворення |
|
|
|
1 |
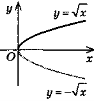
y = -f(х) |
|
Симетрія відносно осі Ох |
|
|
|
2 |
y = f(х) + a |
|
Паралельне перенесення вздовж осі Оу на а одиниць (якщо а > 0, то вгору, якщо а < 0, то вниз) |
|
|
|
3 |
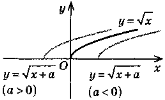
y = f(х + a) |
|
Паралельне перенесення вздовж осі Ох на +а одиниць (якщо а > 0 — вліво, якщо а < 0 — вправо) |
|
|
|
4 |
y = kf(х) (k > 0) |
|
Той самий вигляд, що і y = f(x), тільки розтяг-нуто, якщо k > 1, і стиснуто, якщо 0 < k < 1 |
|
|
|
|
|
|
|
|
Методичний коментар
Одразу слід зауважити, що вивчення питання про геометричні перетворення графіків функцій на даному уроці є досить складним через певну невідповідність програм вивчення геометрії та алгебри у 9 класі. Ця невідповідність існувала у попередньо діючій програмі і, на жаль, збереглася в програмі для 12-річної школи. Тому формування уявлення про геометричні перетворення графіків функцій проводиться на даному уроці на інтуїтивному рівні, і вчителеві не слід акцентувати увагу на строгих означеннях виділених ним видів перетворень. Основна увага приділяється, встановленню і засвоєнню учнями зв'язку між рівнянням функції та певним видом перетворення графіка функції (цей зв'язок відображено в опорному конспекті № 14). Вивчення зв'язку між видом перетворення та рівнянням функції, як це відбувалось останні роки, проводиться через обчислення значень функції в окремих точках і спостереження за зміною значень функції в цих точках залежно від зміни виду функції. Результати даних «спостережень» мають вигляд таблиці (див. опорний конспект № 14).
VI. Формування вмінь
Усні вправи
- Як треба перетворити графік функції y = f(x), щоб утворився графік функції:
1) y = -f(x); 2) y = f(x + 2); 3) y = f(x – 2); 4) y = f(x) + 2;
5) y = f(x) – 2; 6) y = 2f(x); 7) y = ![]() ?
?
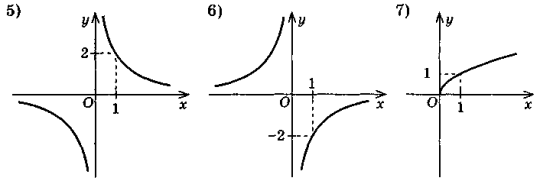
- Дано графіки функцій:
a) y = xa; б) y = ![]() ; в) у =
; в) у = ![]() .
.
Яке рівняння буде мати функція, графік якої утвориться із даних графіків функцій: 1) при паралельному перенесенні вгору на 3 одиниці; 2) при розтягненні в 3 рази; 3) при паралельному перенесенні вправо на 3 одиниці?
Письмові вправи
Зміст вправ, запропонованих до розв'язування на уроці, може бути таким:
- серед заданих графіків функцій вибрати ті, що відповідають даним рівнянням;
- побудувати графік функції, що задана рівнянням, виконавши відповідне до рівняння геометричне перетворення;
- на повторення: дослідити функцію, задану графічно, на монотонність, знайти її нулі, проміжки зростання й спадання та область значень.
(Завдання на побудову графіків функцій шляхом геометричних перетворень на даному уроці мають початковий або середній рівень складності.)
Методичний коментар
Формуванню сталих умінь виконувати побудову графіків функцій шляхом перетворень графіків елементарних функцій має передувати робота з повторення питань про види та особливості графіків елементарних функцій (ця робота проводилась протягом останніх чотирьох уроків). Формування вмінь виконувати побудову графіка функції шляхом геометричних перетворень ведеться паралельно із закріпленням знань учнів про формули, що відповідають цим перетворенням. Тому при виконанні як усних, так і письмових вправ на цьому та наступному уроках вчителеві слід вимагати від учнів в першу чергу аналізу формули даної функції, а потім вже вибору відповідно до неї геометричного перетворення , для побудови графіка функції. Такий підхід, по-перше, сприяє швидшому засвоєнню учнями змісту навчального матеріалу уроку, а по-друге, допомагає попередити помилки, які часто виникають в учнів, особливо, коли мова йде про паралельне перенесення вздовж різних координатних осей.
VII. Підсумки уроку
Контрольне запитання
|
|
Графік якої функції зображений на рисунку? 1) у = х2 + 3; 2) у = х2 – 3; 3) у = -х2 + 3; 4) у = -х2 – 3. |
VIII. Домашнє завдання
- Засвоїти зміст вивчених на уроці перетворень і відповідних формул.
- Розв'язати вправи на застосування цих перетворень (рівень складності та зміст відповідають вправам, розв'язаним на уроці).
- На повторення: вправи на знаходження області визначення функції, нулів функції, проміжків зростання /спадання функції.


про публікацію авторської розробки
Додати розробку