Підсумкові тести з математики за матеріалами 6 класу
Передмова.
…Без прагнення до наукової роботи вчитель елементарної школи неминуче підпадає під владу трьох педагогічних демонів:механічності, рутинності, банальності. Він дерев’яніє, кам’яніє, опускається. А. Дістервег
Розбудова національної школи і поступове впровадження критично-креативної парадигми освіти веде до певної зміни ролі й функцій вчителя у навчально-виховному процесі, зростання його самостійності на різних етапах уроку, що приводить, відповідно, до підвищення відповідальності вчителя за результати своєї праці. Це вимагає певного підвищення професійної майстерності вчителя, доозброєння його новими знаннями, сучасними компетенціями, методами і технологіями, які б дозволили йому перебудувати навчально-виховний процес відповідно до нових вимог і підходів. Особливістю навчання учнів у школі є те, що воно планується, організовується і проводиться вчителем відповідно до вимог Програми і з метою досягнення результатів, які визначенні Державними стандартами. Діяльність вчителя дуже складна і різноманітна. За різними підрахунками, вона містить від 25 до 40 видів конкретних дій. Всі вони впливають на кінцевий результат, хоча їхня роль в ієрархічній структурі процесу навчання не однакова.
Психологи стверджують, що будь-яка свідома діяльність людини складається з трьох етапів: мотиваційно-організаційного(підготовка до виконання певної діяльності з
метою досягнення бажаних результатів), діяльнісно-виконавчого (здійснення дій, які повинні забезпечити досягнення бажаного результату) і контрольно-корекційного(порівняння отриманого результату з бажаним і внесення змін у разі їх невідповідності).
Контольно-корекційний етап
На кожному уроці вчителю потрібний контрольно - корекційний етап (ККЕ) діяльності учнів. Умовно ККЕ може бути трьох видів: ККЕ під час виконавчого етапу діяльності, ККЕ навчального заняття, ККЕ теми або розділу.
Структура ККЕ навчального заняття повинна включати наступні підетапи:
- підетап контролю;
- підетап корекції;
- підетап узагальнення вивченого матеріалу і набутих компетенцій у межах теми;
- підетап виходу, який передбачає оцінювання роботи учнів та інструктаж щодо домашнього завдання.
Підетап контролю. Метою контролю на ККЕ навчального заняття є не оцінювання знань, вмінь та навичок учнів, набутих ними під час вивчення нового матеріалу, а виявлення типових помилок учнів, з’ясування їх причин з метою подальшої корекції. Це здійснюється шляхом порівняння реально досягнутих результатів з очікуваними. Вчитель повинен зафіксувати факт і рівень засвоєння учнями матеріалу, вміння або навичок. На думку В. Беспалько, таким інструментом в руках вчителя може бути тест досягнень, який складається з тестового завдання та зразка повних і правильних відповідей.
 Тести бувають трьох видів: розставляючі, сумативні, формативні. Перші застосовуються для визначення вихідного рівня знань і вмінь учнів і використовуються, як правило, на початку формування в учнів певних знань та навичок. Сумативні тести застосовуються для перевірки засвоєння учнями теми або розділу, оцінюються в балах і використовуються як один із видів тематичної атестації.
Тести бувають трьох видів: розставляючі, сумативні, формативні. Перші застосовуються для визначення вихідного рівня знань і вмінь учнів і використовуються, як правило, на початку формування в учнів певних знань та навичок. Сумативні тести застосовуються для перевірки засвоєння учнями теми або розділу, оцінюються в балах і використовуються як один із видів тематичної атестації.
Формативний тест - це тест для виявлення рівня засвоєння учнями нового матеріалу та оцінювання процесу навчання з метою надання їм оперативної допомоги. Він є тестом середньої складності, охоплює частину матеріалу, має навчальний характер, акцентує увагу на виявленні типових помилок, є основою для організації оперативної корекції, Результати тесту не оцінюються в балах і при виставленні підсумкової оцінки не враховуються. Діяльність учнів здійснюється на І (діяльність з підказкою) і ІІ ( діяльність
по пам’яті) рівні. Цим вимогам відповідають наступні види тестових завдань.
1. «Множинний вибір». Завдання полягає в тому, щоб вказати правильну відповідь із запропонованих. Кількість запропонованих відповідей повинна бути 4 – 5. На думку психологів, це є оптимальна кількість, яка зменшує можливість угадування правильної відповіді й одночасно ускладнює роботи учня.
2. «Тест – впізнання»( або « альтернативний тест»). Це тест І і ІІ другого рівня, коли завдання пропонує зробити вибір між двома можливими відповідями.
3. «Тест - класифікація». Це тест ІІ рівня, який виконується по пам’яті, тобто без підказки. Він полягає в тому, що учню пропонується ряд ознак(рис) споріднених або схожих процесів(явищ), серед яких він повинен відібрати ті, що відповідають певному критерію або вимозі.
4. Тест – підстановка. Це конструктивний тест, який може бути представлений у трьох видах.
Зрозуміло, що, переводячи навчальні цілі у тестові завдання, треба в одному тесті поєднувати різні види подачі тестових завдань.
Інший спосіб контролю відомий з тренінгів. Його суть полягає в тому, що вчитель зачитує по черзі очікувані результати уроку, з якими учні
знайомилися на мотиваційно – організаційному етапі. Якщо учні його досягли, вчитель запитує, як вони діяли, щоб досягти результату. У випадку якщо учні не досягли очікуваного результату, вчитель шляхом фронтальної бесіди з’ясовує, чому так сталося, яка причина цього, що необхідно зробити, щоб виправити становище і досягти очікуваного результату. Тобто рефлексія результатів повинна проводитися не тільки за змістом, але й за способом діяльності учнів.
Підетап корекції. Цей етап має місце у тому випадку, якщо контроль виявив невідповідність отриманого результату очікуваному. Отже, він може бути відсутній у ККЕ.
Корекція – це усунення причин, які привели до появи помилки, з метою приведення реально отриманого результату навчання до рівня очікуваних результатів. До корекції має сенс приступати тоді, коли на попередньому підетапі встановлені помилки і причини їх виникнення.
У зв’язку з тим що головним змістом цього підетапу є не виправлення помилки вчителем або учнями, а усвідомлення учнями причин її виникнення, В.Беспалько слушно вважає, що з боку вчителя це «корекція дидактичного процесу». З огляду на умови проведення ККЕ( необхідність охоплення всіх учнів корекційною діяльністю й обмежений час), цей підетап доцільно провести фронтально, методом евристичної бесіди, методом «Мозкового штурму» або «Мікрофону».
Підетап узагальнення. Зміст роботи вчителя та учнів на цьому етапі полягає в тому, щоб знайти місце для набутих знань, вмінь та навичок у матеріалі теми.
Підетап виходу. Останній підетап ККЕ є по суті інструкцією вчителя учням щодо виконання домашнього завдання.
В другому розділі наведені приклади тестів за курс математики 6-го класу, а також використання тестів на уроці.
Зразки тестів за матеріалами 6-го класу з
математики
ТЕМА 1: ПОДІЛЬНІСТЬ НАТУРАЛЬНИХ ЧИСЕЛ.
1. Дільниками якого числа є числа 2,5,3
А) 260 Б) 418 В)510 Г)845?
2. Яку цифру треба записати замість зірочки в числі 3*4, щоб отримане число було кратне 9
А) 1 Б)2 В)3 Г)9?
3. Виберіть просте число
А)78 Б)1 В)17 Г)91?
4. Скільки дільників має число 17
А)один Б)два В)три Г) сім?
5. Який з запропонованих варіантів є розкладом числа 720 на прості множники
![]() А)52*3*23 Б)5*32*23 В)5*33*22 Г)53*32*2
А)52*3*23 Б)5*32*23 В)5*33*22 Г)53*32*2
6. НСД чисел 24 і 36
А)8 Б) 4 В)6 Г)12?
7.НСК чисел 12 і 15 дорівнює :
А)60 Б)30 В)120 Г)150
8. Які з чисел взаємно прості
А)18 і 12 Б)26 і 21
В) 15 і 27 Г) 14 і 49?
9. Скільки учнів у класі, якщо їх можна поставити в шеренги по 2, по 3 і по 5 учнів
А) 20 Б)25 В)30 Г)24?
Відповіді: 1В,2Б,3В,4Б,5Б,6Г,7А,8Б,9В.
ТЕМА 2: ДОДАВАННЯ І ВІДНІМАННЯ ЗВИЧАЙНИХ ДРОБІВ
1.Яким буде дріб ![]() після скорочення
після скорочення
А) ![]() Б)
Б) ![]() В)
В)![]() Г)
Г) ![]() ?
?
2. Яке з чисел ![]() найменше
найменше
А)1![]() Б)2
Б)2![]() В)
В)![]() Г)2
Г)2![]() ?
?
3. Порівняти дроби ![]() і
і ![]()
А) > Б) < В) =
4. Знаменником суми ![]() і
і ![]() є число :
є число :
А)7 Б)9 В)16 Г)63.
5. Яке число треба поставити замість зірочки,![]() щоб утворилась правильна рівність
щоб утворилась правильна рівність
А) 12 Б)24 В)60 Г)34?
6. Знайти значення виразу ![]()
А)11![]() Б)11
Б)11![]() В) 11
В) 11![]() Г) 11
Г) 11![]() .
.
7.Обчислити:
1) 1-![]()
А) ![]() Б)
Б) ![]() В)
В)![]()
2) 3![]()
А) 3 ![]() Б)3
Б)3![]() В)2
В)2![]()
3) 13 - 7![]()
А) 5![]() Б)5
Б)5![]() В)4
В)4![]()
4) 6![]()
А) 3![]() Б) 3
Б) 3![]() В) 2
В) 2![]()
5) 0,5+![]()
А) ![]() Б)
Б)![]() В)
В)![]()
Відповіді: 1Б,2А,3Б,4Г,5Б,6Г,7:1)Б,2)В,3)В,4)В,5)В
ТЕМА 3:МНОЖЕННЯ ЗВИЧАЙНИХ ДРОБІВ
1. Обчислити добуток дробів:
1) ![]() *5
*5
А)![]() Б)
Б)![]() В)
В)![]()
2) ![]()
А)2![]() Б)
Б) ![]() В)
В)![]()
3) ![]()
А) ![]() Б)
Б)![]() В)
В) ![]()
4)2![]()
А) 2![]() Б)2
Б)2![]() В)2
В)2![]()
2. Спростити вираз:
1) ![]()
А) ![]() Б)
Б) ![]() В)
В)![]()
![]()
2) ![]()
![]()
А) ![]() Б)
Б)![]() В)17
В)17![]()
3)6![]() y
y
А) 6![]() Б)8
Б)8![]() В) 6
В) 6![]()
4) ![]()
А) ![]() Б) 8
Б) 8![]() В) 6
В) 6![]()
![]()
3. Розкрийте дужки:![]()
А) ![]() Б)
Б) ![]() В)
В)![]() .
.
4.Виконайте множення: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() .
.
Відповіді:1:1)А,2)В,3)Б,4)А;
2:1)В,2)В,3)Б,4)Б; 3А;4В.
ТЕМА 4: ДІЛЕННЯ ЗВИЧАЙНИХ ДРОБІВ
1.Вказати число, обернене до числа![]() :
:
А) ![]() Б)
Б)![]() В)
В) ![]() .
.
2. Знайти частку:
1) ![]()
А) ![]() Б)
Б)![]() В)
В)![]()
2) ![]()
А) ![]() Б)
Б)![]() В)
В)![]()
3) ![]()
А) ![]() Б)
Б)![]() В)
В)![]()
4) ![]()
А) ![]() Б)
Б)![]() В)
В)![]()
5) ![]()
А) ![]() Б)
Б)![]() В)5
В)5![]()
3.Знайти значення x: 4x=![]()
А) ![]() Б)
Б)![]() В)
В)![]() .
.
4.Визначте,які із запропонованих чисел є взаємно оберненими:
А) 1,4 і ![]() Б) 0,4 і
Б) 0,4 і ![]() В)1,2 і
В)1,2 і ![]()
5.Виконайте ділення (буквами позначено натуральні числа) ![]()
А) ![]() Б)
Б)![]() В)
В)![]()
Відповіді:1В,2:1)Б,2)Б,3)А,4)А,5)А;3В,4В,5Б.
ТЕМА 5: ВІДНОШЕННЯ І ПРОПОРЦІЇ
1.Знайти значення відношення 0,5 до 0,4:
А)![]() Б)1,25 В)0,2
Б)1,25 В)0,2
2. Знайти відношення, що дорівнює відношенню 0,8:0,2
А)1![]() Б)16:5 В)6:1
Б)16:5 В)6:1![]()
3. Запишіть у вигляді пропорції висловлення: 2 відноситься до 7, так само як 6 відноситься до 21:
А) 2:6=7:21 Б)2:7=6:21 В)2:21=7:6
4. Яка з пропорцій істина:
А)24:30=28:36 Б)1![]()
В)2,5:2=4:32?
5.Вкажіть крайні члени пропорції ![]() :
:
А)18 і 36 Б)18 і 16 В)18 і 56.
6. Знайти невідомий член пропорції
1) x:5=21:15.
А) 63 Б)7 В)36
2) ![]()
А) 27 Б) 12 В) 5![]() .
.
7. Розв’яжіть задачу:
Сталева кулька об’ємом 5см3 має масу 39 грамів. Яку масу має кулька об’ємом 2,5см3, зроблена з тієї ж самої сталі?
А)195г Б)1,95г В)19,5г
Відповіді: 1Б,2В,3Б,4Б,5В,6:1)Б,2)А,7В.
ТЕМА 6: ВІДСОТКОВІ РОЗРАХУНКИ. ПРЯМА І ОБЕРНЕНА ПРОПОРЦІЙНІСТЬ
1. Із 200г цукрових буряків виходить 37 кг цукру. Скільки потрібно буряків, щоб одержати 185 кг цукру?
А)600кг Б)40кг В)1000кг
2. Сплав містить 12% цинку. Скільки кілограмів цинку міститься у 80 кг сплаву?
А) 12,4 кг Б)15 кг В)9,8 кг.
3. У саду росло 324 дерева, з яких 25% становили яблуні. Скільки яблунь росло в саду?
А)162 Б) 81 В)243
4. Скільки відсотків становить число 24 від числа 36:
А)8![]() Б)66
Б)66![]() В)82%?
В)82%?
5.На скільки процентів збільшиться число, якщо його збільшити вдвічі:
А)на 50% Б)на 100% В)на 200%.
6.Для будівництва стадіону 5 бульдозерів розчистили майданчик за 240 хвилин. За який час 7 бульдозерів розчистять цей майданчик?
А) 60хв. Б)294хв. В)150хв.
Відповіді:1В,2В,3Б,4Б,5Б,6В.
ТЕМА 7: ЙМОВІРНІСТЬ ВИПАДКОВОЇ ВЕЛИЧИНИ.
1. Вкажіть малоймовірну подію:
А)крокодил навчиться співати
Б)після суботи буде неділя
В)виграти в розіграші лотереї
2. Яку ймовірність того, що ти народився в п’ятницю:
А) ![]() Б)
Б)![]() В)1 Г)
В)1 Г)![]() .
.
3.Ймовірність вірогідної події дорівнює:
А)![]() Б)1 В)0.
Б)1 В)0.
4.Яка ймовірність того, що при одному підкиданні грального кубика випаде кількість очок, що дорівнює:
1) двом
А) ![]() Б)
Б)![]() В)
В)![]()
2) п’яти
А) ![]() Б)
Б)![]() В)
В)![]()
3) непарному числу
А)![]() Б)
Б)![]() В)
В) ![]()
4) числу, яке кратне 6
А)![]()
![]() Б)
Б)![]() В)
В)![]() .
.
Відповіді: 1В,2Б,3Б,4:1)Б,2)А,3)Б,4)А.
ТЕМА 8: КОЛО. КРУГ.
1.На якому малюнку зображено коло?

 А) Б) В)
А) Б) В)

![]()
2. Який відрізок є :
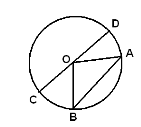
1)діаметром
А) АВ Б) DC В)ОА
2) радіусом
А) АВ Б) DC В)ОА
3) хордою
А) АВ Б) DC В)ОА
3.Знайдіть радіус кола, діаметр якого становить 8 см:
А) 8см Б)16см В)4см
4. Вкажіть формулу за допомогою якої можна обчислити довжину кола:
А) d=2R Б)l=2![]() R В) S=
R В) S=![]() R2
R2
5.Чому дорівнює площа круга, радіус якого 10см:
А) 62,8см2 Б)314см2 В)31,4см2
6.Знайдіть довжину кола, діаметр якого становить 8дм:
А)12,56дм Б)50,24дм
В)25,12дм.
Відповіді:1А,2:1)Б,2)В,3)А;3В,4Б,5Б,6В.
ТЕМА 9: РАЦІОНАЛЬНІ ЧИСЛА. КООРДИНАТНА ПРЯМА. ПОРІВНЯННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ.
1.Яке з чисел є додатним :
А)-1,2 Б)0 В)+3,4
2. Вкажіть протилежні числа:
А) 5 і ![]() Б) +7 і 7 В)-3 і 3
Б) +7 і 7 В)-3 і 3
3.Чому дорівнює модуль числа -13:
А) -13 Б)13 В)1,3?
4. Виберіть правильне твердженн
![]()
А) К(5), М(1,5), D(-4)
Б) D(-4), M(2), K(4)
B) K(-5), D(4), M(-1,5).
5.Виберіть неправильне твердження:
А)4,14 – додатне число
Б)4,14 – раціональне число
В)0 – ціле число
Г) -4 – натуральне число.
6. Знайти значення p, якщо –p=-18:
А)18 Б)-18 В)1,8.
7. Скільки розв’язків має рівняння ІxІ=12:
А)один Б)два В)жодного.
8. Який знак треба поставити між числами:
1) -58 і 43
А) > Б)< В) =
2) -92 і -89
А) > Б)< В) =
3) -![]() і 0
і 0
А) > Б)< В) =
4) -1,1 і -1,099
А) > Б)< В) =
Відповіді:1В,2В,3Б,4В,5Г,6А,7Б,8:1)Б,2)Б, 3)Б,4)Б.
ТЕМА 10: РАЦІОНАЛЬНІ ЧИСЛА. ДОДАВАННЯ І ВІДНІМАННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ.
1.Виконайте додавання :
1)-9+6
А)3 Б)-3 В)15
2)-6+(-20)
А)-26 Б)-14 В)14
3)-1,8+1,8
А)-3,6 Б) 0 В)3,6
2. Знайти значення виразу 43+(-60)-21 :
А) 124 Б) -82 В) -38
3. Виконайте віднімання:
1) 10-16
А)6 Б)-6 В)26
2)3,5-(-9,7)
А)6,2 Б)-6,2 В)13,2
3)0-7,25
А)7,25 Б)0 В)-7,25
4)0-(-0,08)
А)0,08 Б)-0,08 В)0
5)-5,3-3,7
А)1,6 Б)-1,6 В)-9
4. Розв’яжіть рівняння -4,5-x=9
А) 13,5 Б)-13,5 В)4,5
Відповіді: 1:1)Б,2)А,3)Б;2В;3:1)Б,2)В,3)В,4)А,5)В;4Б.
ТЕМА 11: РАЦІОНАЛЬНІ ЧИСЛА. МНОЖЕННЯ І ДІЛЕННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ.
1. Знайти добуток:
1) -12.5
А)60 Б)-17 В)-60
2)-2,3.(-1,4)
А)-3,7 Б)-3,22 В)-9,2
А)-1,28 Б)0,02 В)-2,58
2. Виконайте дії: -3,2.0,4+(-2,6).(-0,5)
3. Знайдіть значення степеня:
1) (-2)5
А) 10 Б)-10 В)-32
2) (1![]() )3
)3
А)-1![]() Б)-1
Б)-1![]() В)-3
В)-3![]()
3) (-1)10
А) -1 Б)1 В)-10
4. Назвати коефіцієнт виразу -7,2b
А)-7,2 Б)7,2 В) -7,2b
5. Спростити вираз і вказати його коефіцієнт
-3,2p. (-0,5k)
А) -3,2 Б)-3,7 В)1,6
6. В якій з рівностей правильно застосовано розподільну властивість
А) (-5-7). 6 = -30+42
Б) (m-n). (-2) = -2m - 2n
В)-5(p-k+9) = -5p+5k-45?
7. Розкрийте дужки -2(a+3b-4)
A)-2a+6b+8
Б)-a-6b-8
B)-2a-6b+8
Відповіді: 1:1)В,2)Б;2Б,3:1)В,2)Б,3)Б;4А,5В,6В,7В.
ТЕМА 12: РАЦІОНАЛЬНІ ЧИСЛА. ДІЛЕННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ.
1. Знайдіть частку:
1)-36:9
А)4 Б)-4 В)6
2)-21: (-14)
А)3![]() Б)
Б)![]() В)-1,5
В)-1,5
2. Розв’яжіть рівняння -3,78:х=-0,6
А) 3,18 Б)8,8 В)2,268
3. Виконайте дії -5,4:0,6+9,6: (-0,8)
А)-21 Б)-9 В)3
4. Розв’яжіть рівняння ІхІ·(-1,2)=-4
А) 4,8 Б) -4,8
В)4,8 і -4,8
5. Знайдіть значення змінної :
-1,9y+0,6y-0,5y=0,54
А)-1,8 Б)-0,3 В)1,8.
6.Обчислити значення виразу ![]()
А)2,5 Б)-5,5 В)![]()
Відповіді: 1:1)Б,2)А;2Б,3А,4В,5Б,6Б.
ТЕМА 13: РІВНЯННЯ.
1. Виконайте перенесення доданків з невідомими в ліву частину рівняння 3x=7+5x:
А) -3х=7 Б)-7=3х В)7х=7.
2. Знайдіть корінь рівняння:
1)3х+7=х+5
А)3 Б)-1 В)6
2)5-1,2х=х-6
А)5 Б)-1,2 В)1,2
3. Розкрийте дужки і виконайте перенесення доданків у рівнянні
12-4(х-3)=39-9х
А)12-4х+12=39-9х
-4х-9х=39+12+12
-13х=63
Б)12-4х-12=39-9х
-4х+9х=39+12-12
5х=39
В)12-4х+12=39-9х
-4х+9х=39-12-12
5х=15
4.Яке з рівнянь відповідає умові задачі:
Дріт довжиною 350м розрізали на дві частини так, що одна з них виявилась на 6м коротша за іншу. Знайти довжини частин.
А)х+6х=350
Б)х+(х+6)=350
В)х+х: 6=350
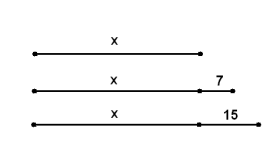
![]() 5. За малюнком складіть рівняння і розв’яжіть його:
5. За малюнком складіть рівняння і розв’яжіть його:
![]()

![]()
![]()
![]()
А)х+(х+7)+(х+15)=124
Б)х+7х+15х=124
В)3х=124
Відповіді :1А,2:1)А,2)А,3В,4Б,5А,
ТЕМА 14: ПЕРПЕНДИКУЛЯРНІ ПРЯМІ І ПАРАЛЕЛЬНІ ПРЯМІ. КООРДИНАТНА ПЛОЩИНА.
![]()
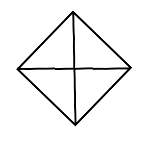
MNKP-квадрат
![]()
![]()
![]()
![]()
![]()
1.Використовуючи рисунок вкажіть перпендикулярні прямі:
А)MNі KP Б)MN і NK В)MP і NK
2. За рисунком вкажіть паралельні прямі
А) MN,KP Б)NK,KP B)MP,MN
3.Горизонтальна вісь координатної площини називається :
А)вісь OY Б)вісь ординат
В)вісь абсцис
4. В якій чверті знаходиться точка з координатами (-3;7)
А) І Б)ІІ В)ІІІ Г)IV.
5. Де розташована точка з координатами (0;0)
А) на вісі ординат Б) на вісі абсцис
В)на початку відліку
6. З точок А(2;4), В(1;-10), С(0;-20), D(-4;-50), F(0;7), Е(47;0), S(-9;7), P(-6;0) виберіть точки, що лежать
1)на вісі ОХ
А) C,E,F,P Б) Е,Р В) С,F
2) лівіше від осі OY:
А) D,S,P Б)B,C,D B)A,D
Відповіді:1Б,2А,3В,4Б,5В,6:1)Б,2)А.
ПІДСУМКОВИЙ УРОК ЗА ТЕМОЮ «ЗВИЧАЙНІ ДРОБИ»
Мета: навчити поєднувати математичну і нематематичну інформацію, удосконалювати знання учнів про звичайні дроби; розвивати логічне мислення, навички усної лічби, математичну мову; виховувати інтерес до нових знань і прагнення їх набувати.
Обладнання: планшети, тести.
Хід уроку
І. Організаційний момент
ІІ. Повідомлення теми, мети уроку.
Ш.Історичні повідомлення ( готують учні )
1. Дробові числа в Єгипті були відомі ще 4000 років потому. Записували їх тоді тільки одиничними дробами( тобто такими ,чисельники яких дорівнюють одиниці) або сумами одиничних дробів. Наприклад, дріб 2/5 13єгиптяни писали 1/3 + 1/15 , а дріб 2/13 у вигляді суми 1/8 , 1/52 і 1/104.
2.ажливими і найбільш вживаними були дроби ![]() .Такі дроби відіграли визначну роль у музиці. І сьогодні в загальноприйнятому запису найдовша за звучанням ціла нота ділиться на половини, чверті, восьмі, шістнадцяті.
.Такі дроби відіграли визначну роль у музиці. І сьогодні в загальноприйнятому запису найдовша за звучанням ціла нота ділиться на половини, чверті, восьмі, шістнадцяті.
3 Давньогрецькі математики розглядали числа, які зараз записують у вигляді дробів, але називали їх відношеннями. Римляни користувалися дробами із знаменниками 12, які називали унціями. Коли казали «5 унцій» або «13 унцій» , то мали на увазі 5/12 або 13/12.
4.У Китаї дроби називали , користуючись словом «половина» : ![]() .У Греції та Єгипті довгий час користувались дробами з чисельником 1, вавілоняни із знаменником 60.
.У Греції та Єгипті довгий час користувались дробами з чисельником 1, вавілоняни із знаменником 60.
5. Слова «чисельник» і «знаменник» вперше з’явились в ХІІІ ст., «скорочення дробу» і «зведеня дробів до спільного знаменника» - в ХV ст.., а «правильні» і «неправильні» дроби – в ХVІІІ. В Україні спочатку використовували тільки одиничні дроби. Але й зараз дроби ![]() називають «половиною», «третиною», «четвертиною» . Числа 1
називають «половиною», «третиною», «четвертиною» . Числа 1![]() - півтора, 2
- півтора, 2![]() - пів третина, 4
- пів третина, 4![]() - пів п’ята.
- пів п’ята.
IV. Актуалізація опорних знань
А) Фронтальне опитування учнів :
1.Які числа називаються звичайними дробами?
2.Що позначає риска дробу?
3 Що називається знаменником дробу і на що він вказує?
4.Що називається чисельником дробу і на що він вказує?
5.Який дріб називається правильним?
6.Який дріб називається неправильним?
7.![]() записати у вигляді правильного дробу.
записати у вигляді правильного дробу.
8.![]() записати у вигляді неправильного дробу.
записати у вигляді неправильного дробу.
Б) Робота на планшетах:
1. Записати неправильний дріб із знаменником 5.
2. Виконати дії :
а)![]() г)
г)![]()
б)![]() д)
д)![]()
в)1-![]()
V. Тестування.
-
У дробі
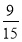 знаменником є:
знаменником є:
а) 9 б) 15 в) 24 г) ![]()
2. Який із написаних дробів є неправильним?
![]() а)
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
3. На 3 і 5 ділиться число:
а) 205 б) 710 в) 925 г) 405
4. Яка з нерівностей є правильною:
а) ![]() >
>![]() б)
б) ![]() <
<![]() в)
в) ![]() <
<![]() г)
г) ![]() <
<![]()
![]()
5. ![]() =
=
а) ![]() б)
б) ![]() в) 2 г)
в) 2 г) ![]()
6. ![]() +
+![]() +
+![]() =
=
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
7. ![]() -
- ![]() =
=
а) ![]() б)
б) ![]() в) 1
в) 1![]() г) 1
г) 1![]()
8. ![]()
![]() =
=
а) ![]() б)
б) ![]() в) 1
в) 1![]() г)
г) ![]()
9. 2![]()
![]()
![]() =
=
а) ![]() б) 1
б) 1![]() в) 2
в) 2![]() г)
г)![]()
10. ![]() :
:![]() =
=
а) ![]() б) 13
б) 13![]() в) 6 г)
в) 6 г) ![]()
11.6![]() :2=
:2=
а) 3![]() б) 6
б) 6![]() в) 3
в) 3![]() г) 3
г) 3![]()
12.Якщо 5 : х = ![]() , то х дорівнює:
, то х дорівнює:
а) 6 б) 294 в) 4![]() г) 60
г) 60
Клас розбиваємо на групи:
1-а група: фахівці (перевірка виконання тестових завдань) ;
2-а група: філологи (завдання « Чи правильно ми говоримо?»);
3-я група: веселуни ( веселі задачі) ;
4-а група: розумники ( розгадування кросворду) ;
5-а група: практики (розв’язування практичних задач) ;
6-а група: кодувальники (задачі клоуна).
VI. Чи правильно ми говоримо?
Прийшов тато з міста, дає сину медівника та й каже:
- На, Васильку, та поділися з Петриком по щирості!
- А як діляться по щирості? – запитує Василько.
- Отак, сину, - каже тато, - більшу половину даси Петрику, а меншу – візьмеш собі.
- То дайте Петрику медівника, нехай він ділиться по щирості.
Чи правильно тут використовується термін «половина»?
Чи може бути одна половина меншою, а друга – більшою?
Слід говорити: більша частина, менша частина, оскільки половини мають бути однаковими. Адже дріб ![]() означає половину.
означає половину.
Назвіть дроби, які дорівнюють ![]() .
.
![]()
![]() .
.
VII. Веселі задачі
1.Скільки буде, якщо ми цілий пиріг поділимо на 2 частини?
- на 4 частини?
- на 8 частин?
- На 16 частин?
На 64 частини? (Або крихти).
2.У мами дві доньки й один синок. Донечці пиріжечок, другій теж пиріжечок. А синочку? Ой, забула? Хай кожна сестриця дасть братові половинку. Так і зробили. То кому краще?
3.Великий російський письменник Л. М. Толстой писав, що людину можна оцінювати дробом, знаменник якого складає те хороше, що вона думає про себе сама, а чисельник – те хороше, що думають про неї інші! Як ви вважаєте, чи правильно це?
(Учні висловлюють свою думку.)
VІІІ. Кросворд (ключове слово виділене – Буняковський)
1.Закінчити речення:
«Числа ![]() ;
; ![]() ;
; ![]() ;
; ![]() називають….
називають….
2. Одиниця вимірювання кутів.
3. Найменше натуральне число.
4. Дробову риску можна розуміти, як знак…
5. Ділення чисельника і знаменника дробу на їх спільний дільник.
6. Результат множення.
7. Дріб, у якому чисельник менший від знаменника.
8. Число записане над рискою дробу.
9. Знаменник, до якого зводять дроби при додаванні з різними знаменниками.
10. Компонент дії додавання.
12. Відстань між кінцями відрізку.
13. Закон множення для трьох множників.
Розповідь вчителя.
Віктор Буняковський один з провідних математиків 30 – 50 років 19 століття народився 3 грудня 1804 року в містечку Бар Подільської губернії. У 1921 році Віктор опинився у Парижі. В Сорбоні і в коледжі Буняковський вивчив математику під керівництвом Лапласа, Пуассона, Фур’є, Ампера та ін. Але найбільше він займався математикою у Коші. Буняковський зробив численні відкриття в теорії ймовірностей, з якою ми познайомимся при вивченні наступної теми.
IХ Задачі клоуна.
Через два дні до нас у місто приїжджають артисти цирку. Ви, мабуть, хочете дізнатись трохи про гостей, які незабаром завітають до нас. Вони прислали розповідь про себе, але її треба розшифрувати.
Я веселий клоун . Мій зріст ![]() ( назви його в метрах). Мій друг важить годинах).А після вистави ви зможете з’їсти у кафе
( назви його в метрах). Мій друг важить годинах).А після вистави ви зможете з’їсти у кафе ![]() морозива (назви у кілограмах). Ми продали 576 білетів, що становить
морозива (назви у кілограмах). Ми продали 576 білетів, що становить ![]() усіх білетів. Скільки всього білетів ми продали?
усіх білетів. Скільки всього білетів ми продали?
Х. Розв’язування практичних задач.
1. Галина Василівна залишила дітям на столі сливи. Прокинувся Микола, з’їв 9 слив, що становить ![]() усіх слив. Потім Володя з’їв
усіх слив. Потім Володя з’їв ![]() того, що було, а Катя -
того, що було, а Катя - ![]() того, що залишилося. Скільки слив на тарілці залишилось?
того, що залишилося. Скільки слив на тарілці залишилось?
2.Відстань від дому до школи 1км 300м . 1км Василь пройшов за ![]() од. До дзвінка залишилось 8 хвилин . Чи встигне дійти до школи Василь з тією самою швидкістю?
од. До дзвінка залишилось 8 хвилин . Чи встигне дійти до школи Василь з тією самою швидкістю?
3. Маса слона 5т. Маса миші – 50г. Отже , миша більша від слона у 50:5 =10 разів? Яку частину становить маса миші від маси слона ?
4. Назвати дроби менші за ![]() .
.
5. Чи можна назвати найбільший дріб ?
ХІ. Оцінювання учнів.
ХІІ. Підсумок уроку.
У давнину дії зі звичайними дробами викликали великі труднощі. Вавілоняни пояснювали це «втручанням злих духів». Англійський чернець Бєда , який був досить освідченню людиною свого часу, писав:»У світі є багато речей , але немає нічого важчого, як чотири дії арифметики.». Тоді ж , мабуть виникло німецьке прислів’я :«Потрапити у дроби», що означало – опинитися у скрутному становищі. А причина цих труднощів, полягала в тому, що не було відповідної теорії.
Я думаю ,що ви не потрапите в скрутне становище через дроби, оскільки вмієте виконувати дії над ними, і ваші знання з кожним роком будуть поповнюватися. Спасибі вам за урок, ви гарно на ньому попрацювали.
КОНСПЕКТ УРОКУ З АЛГЕБРИ В 7 КЛАСІ
Тема: Розв’язування систем лінійних рівнянь з двома змінними.
Мета: Закріпити знання учнів про системи лінійних рівнянь з двома змінними, формувати навички розв’язання систем способом підстановки, розвивати логічне мислення, активізувати пізнавальну діяльність; формувати навички правильної математичної мови, вміння аналізувати результати власної роботи та роботи однокласників; виховувати старанність, самостійність; сприяти формуванню особистості.
Тип уроку: урок формування вмінь та навичок.
Обладнання: картки з диференційованими завданнями, планшети, сигнальні картки: рожевий колір – мені багато не зрозуміло, жовтий колір – зрозумів, але є незрозумілі моменти, зелений колір – я все зрозумів.
І. Мотивація навчальної діяльності, позитивний настрій на урок. Формулювання теми і мети уроку.
За словами відомого французького письменника:» Вчитись треба тільки весело: щоб переварити знання, треба поглинати їх з апетитом». Отже, давайте ми сьогодні на уроці отримаємо задоволення і знання про спосіб підстановки та його застосування.
Вчитель просить учнів на планшетах зобразити свій настрій з яким вони прийшли на урок.
Мета нашого уроку полягає в тому, щоб перевірити знання про системи лінійних рівнянь з двома змінними і навчитися розв’язувати системи способом підстановки.
ІІ. Актуалізація опорних знань.
- Записати на планшеті приклад системи лінійних рівнянь з двома змінними.
- Дати відповідь на питання:
- Що називається системою рівнянь з двома змінними?
- Що є розв’язком системи рівнянь з двома змінними?
- Доберіть розв’язок системи лінійних рівнянь
![]() х + у = 1,
х + у = 1,
х – у = 1.
Відповідь запишіть на планшеті.
- Скільки розв’язків має кожна система
![]()
![]() х + у = 1, х + у = 1,
х + у = 1, х + у = 1,
2х + 2у = 4. 2х + у = 0.
Відповідь записати на планшеті.
![]() 5. Розв’язати способом підстановки систему х + у = 1,
5. Розв’язати способом підстановки систему х + у = 1,
х – у = 1.
(перевірка в парах за зразком на дошці)
Використовуємо сигнальні картки для виявлення експертів та степеня розуміння теми учнями.
6. Алгоритм позв’якання системи способом підстановки.(опитування методом «Мікрофон»)
7. Самостійна робота з тестовими завданнями ( перевіряють експерти, виконують аналіз роботи ).
Самостійна робота
І варіант
![]() 1. Скільки позв’язів має система х – 2у = 4,
1. Скільки позв’язів має система х – 2у = 4,
3х – 6у = 12.
А) жодного Б) один В) два Г) безліч
![]() 2. З даних пар вибрати розв’язок системи х + у = 7,
2. З даних пар вибрати розв’язок системи х + у = 7,
х – у = 3.
А) (3;4) Б) (4;3) В) (2;5) Г) (5;2)
3. З даного рівняння виразити х через у : 2х – у = 12.
А) х = 6 +0,5у Б) х = 6 – у
В) х = 6 + у Г) х = 6 – 0,5у
![]()
![]() 4. Вставити пропущене число (2 ; ) так, щоб отримана пара чисел була розв’язком системи рівнянь: у + х = 0,
4. Вставити пропущене число (2 ; ) так, щоб отримана пара чисел була розв’язком системи рівнянь: у + х = 0,
4х + у = 6.
![]() 5. Виконати підстановку в системі 2х + у = 11,
5. Виконати підстановку в системі 2х + у = 11,
5х – 2у = 41.
6.Заповнити пропуски:
![]()
![]()
![]() 2х + у = 8, у = 8 – 2х, у = 8 – 2х,
2х + у = 8, у = 8 – 2х, у = 8 – 2х,
х – у = 1; х – (---------) = 1; х – 8 + 2х
![]()
![]()
![]() у = ------------, у = ------------, у = ------------, 3х = 1 + -----; 3х = 9; х = 3;
у = ------------, у = ------------, у = ------------, 3х = 1 + -----; 3х = 9; х = 3;
![]() у = -----,
у = -----,
х = -----.
Відповідь: ( 3; -----).
ІІ варіант
![]() 1. Скільки розв’язків має система 2х – 3у = 2,
1. Скільки розв’язків має система 2х – 3у = 2,
- х + 1,5у = 1.
А) жодного Б) один В) два Г) безліч
![]()
2. Яка з пар є розв’язком системи х – у = 1,
х + у = 5.
А) (4;3) Б) (2;3) В) (3;2) Г) (3;4)
3. Вставити число, щоб пара чисел ( 1; -1) була розв’язком системи
![]()
х – 2у = 3,
![]() х + у = 4.
х + у = 4.
4. З даного рівняння х – 5у = 10 виразити у.
А) у = 2 – х Б) у = 2 + х
В) у = - 2 – 0,2х Г) у = - 2 + 0,2х
![]() 5. Виконати підстановку в системі 6х – 3у = 4,
5. Виконати підстановку в системі 6х – 3у = 4,
2х + у = 5.
6. Заповнити пропуски:
![]()
![]()
![]() 3х + у = 1, у = 1 -2х, у = ----------,
3х + у = 1, у = 1 -2х, у = ----------,
у – х = -5; (----------) – х = -5; 1 – 2х – х = -5;
![]()
![]()
![]() у = ----------, у = ----------, у = -----,
у = ----------, у = ----------, у = -----,
-3х = -----; х = ----- : (-3); х = 2.
Відповідь: (2: ----- ).
Самооцінка виконання письмової роботи: сигнальні картки.
ІІІ. Формування навичок розв’язування систем.
1. Клас ділимо на групи по 6 учнів. Групи отримують завдання рівнів А, Б,В , де рівні А та Б відповідають середньому та достатнім рівням, а В – високому.
![]()
![]() (А) 4х + 5у = -1, (Б) 5х +2у = 1,
(А) 4х + 5у = -1, (Б) 5х +2у = 1,
2х + у = 13. 2х – 4у = 10.
![]() (В) 10 – (2х – 3у) = 3(2х +у),
(В) 10 – (2х – 3у) = 3(2х +у),
2(7у – 5) = -8(х + 1).
Звіти керівників груп, демонстрація розв’язку на дошці.
Використовуємо сигнальні картки.
2. Розв’язування системи способом підстановки « ланцюжком».
![]() 3(х – 1) – 2(у + 2) = 3,
3(х – 1) – 2(у + 2) = 3,
3(х + 1) – (у – 2) = 10.
ІV. Підсумки уроку.
- Експерти доповідають про виконання самостійної роботи.
- Оцінювання учнів: проводиться експертами та керівниками груп.
- Рефлексія
- Що ми сьогодні робили на уроці?
- Як ми це робили?
- Чи досягли мети уроку?
- ЯК вам працювалося у парах?
- Які питання виникали під час виконання завдань?
- Вчитель пропонує учням зобразити на планшетах свій настрій в кінці уроку.
V. Домашнє завдання задається аналогічне до завдань, що виконували по групах.
Висновки
ККЕ повинен проводитися і після навчального заняття, і після вивчення теми або розділу. Останній відзначається тим, що , як правило, охоплює два уроки: перший – це підсумково – узагальнюючий урок з теми, а другий - це урок тематичної атестації. Пісумково – узагальнюючий урок з теми має ту саму мету, структуру і завдання, як і ККЕ навчального заняття, але в його основу покладено пошук відповіді на основне питання теми, спираючись на повторення й узагальнення відповідей, здобутих під час окремих уроків.
1


про публікацію авторської розробки
Додати розробку
