Підсумковий урок з теми «Чотирикутники»
Тема. Підсумковий урок з теми «Чотирикутники»
Мета: повторити, систематизувати й узагальнити набуті під час вивчення теми «Чотирикутники» знання учнів щодо означень, властивостей та ознак таких понять, як чотирикутник, паралелограм, прямокутник, ромб і квадрат; узагальнити й систематизувати вміння учнів щодо застосування вивчених теоретичних тверджень для розв'язування задач.
Тип уроку: узагальнення та систематизація знань.
Наочність та обладнання: конспекти 1 – 4.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Вчитель збирає зошити із виконаною самостійною роботою, а також проводить перевірку виконання самостійної роботи та корекційну роботу (для цього учням пропонується до уваги правильне розв'язання задач самостійної роботи або записане на дошці заздалегідь, або виконане у формі роздавального матеріалу — на окремих аркушах містяться ксерокопії правильних розв'язань задач самостійної роботи).
III. Формулювання мети і завдань уроку
Основна дидактична мета та завдання на урок цілком логічно випливають із місця уроку в темі — оскільки урок є останнім, підсумковим, то головним є питання про повторення, узагальнення та систематизацію знань, набутих учнями в ході вивчення теми «Чотирикутники». Таке формулювання мети створює відповідну мотивацію діяльності учнів.
IV. Повторення та систематизація знань
Залежно від рівня підготовки учнів роботу на уроці вчитель може організувати різними способами. Можна провести самостійну роботу за теоретичним матеріалом (наприклад, за підручником або за конспектом повторити зміст основних понять теми або ж скласти схему, що відображає логічний зв'язок між основними поняттями теми).
Можна провести гру «Закінчи речення» або «Інтелектуальний аукціон» (кожний лот — це певне поняття, наприклад паралелограм; торги починаються з того, що хтось з учнів формулює одне із вивчених тверджень; наступний учень має «переробити» відповідь попереднього, сформулювавши інше твердження; перемагає той, хто назве останнє твердження, яке ніхто не зможе «переробити»), або провести опитування у формі інтерактивної вправи.
Орієнтовний перелік запитань для опитування
- Чи існує чотирикутник, кути якого дорівнюють 100°, 80°, 135°, 55°?
-
У чотирикутнику ABCD
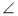 А =
А = 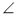 С. Чи правильно, що ABCD — паралелограм?
С. Чи правильно, що ABCD — паралелограм?
-
У паралелограмі ABCD
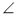 А +
А + 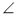 С > 180°. Назвіть гострі кути паралелограма.
С > 180°. Назвіть гострі кути паралелограма.
- Діагоналі чотирикутника ABCD перетинаються в точці О, AB = CD, AB || CD. Назвіть пари рівних відрізків з кінцем у точці О. Відповідь обґрунтуйте.
- Чи будь-який квадрат є ромбом?
- Чи правильно, що існує прямокутник, який не є паралелограмом?
- Три кути паралелограма рівні. Визначте вид паралелограма.
(Під час виконання цієї роботи активно використовується наочність: конспекти, складена на попередньому уроці схема тощо). Підсумком роботи є повторення та систематизація знань, які учні здобули в ході вивчення теми.
Систематизація знань учнів полягає в тому, щоб сформувати в учнів певні загальні підходи до застосування знань на практиці (розв'язування задач) як у стандартних, так і в нестандартних ситуаціях.
Застосування знань учнів у стандартних ситуаціях
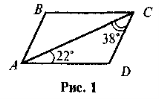
- За даними рис. 1 знайдіть кути паралелограма ABCD.
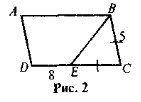
- За даним рис. 2 знайдіть PAKD.
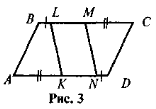
- На рис.3 KLMN — паралелограм. Доведіть, що ABCD також с паралелограмом.
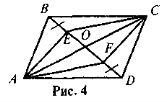
- На рис. 4 ABCD — паралелограм. Доведіть, що AE || CF.
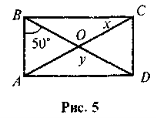
- На рис. 5 ABCD — прямокутник. Знайдіть кути х і у.
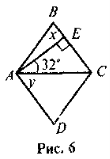
- На рис. 6ABCD— ромб. Знайдіть кути х і у.
-
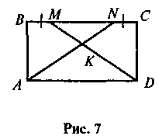
На рис. 7 ABCD — прямокутник. Доведіть, що трикутник AKD —
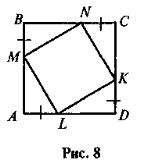
рівнобедрений. - На рис. 8 ABCD — квадрат. Доведіть, що MNKL також є квадратом.
Застосування знань учнів у нестандартних ситуаціях
-
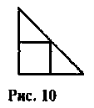
 Через точку, яка належить стороні рівностороннього трикутника, проведені прямі, паралельні двом іншим його сторонам. Визначте периметр паралелограма, що утворився, якщо периметр трикутника дорівнює 18 см.
Через точку, яка належить стороні рівностороннього трикутника, проведені прямі, паралельні двом іншим його сторонам. Визначте периметр паралелограма, що утворився, якщо периметр трикутника дорівнює 18 см.
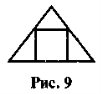
- У рівнобедрений прямокутний трикутник вписано квадрат так, що дві вершини квадрата лежать на гіпотенузі, а дві інші — на катетах (рис. 9). Знайдіть гіпотенузу трикутника, якщо сторона квадрата дорівнює 2 см.
-
У рівнобедрений прямокутний трикутник вписано квадрат так,
що вони мають спільний прямий кут (рис. 10). Знайдіть пери
метр квадрата, якщо катет трикутника дорівнює 4 см.
V. Підсумки уроку
Основним підсумком уроку має бути усвідомлення учнями основного кола задач, які вони мають уміти розв'язувати із використанням знань, набутих у ході вивчення теми.
VI. Домашнє завдання
Повторити зміст вивчених теоретичних відомостей. Виконати домашню контрольну роботу (див. підручник).


про публікацію авторської розробки
Додати розробку
