Розв'язування задач на означення, властивості та ознаки трапецій
Тема. Розв'язування задач на означення, властивості та ознаки трапецій
Мета: закріпити знання учнів про означення, властивості та ознаки трапецій, відпрацювати навички застосування вивчених тверджень під час розв'язування задач із застосуванням властивості катета, що лежить проти кута 30°.
Тип уроку: комбінований.
Наочність та обладнання: конспект «Трапеція. Види трапецій».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
З метою урізноманітнення та пожвавлення роботи з перевірки домашнього завдання цей етап уроку проводимо у вигляді гри «Знайди помилку» (учням пропонується знайти та виправити помилки в розв'язаннях домашніх задач за готовими зразками «розв'язань». Помилки у «розв'язаннях» мають відтворювати ситуації, за яких учні припустилися найбільшої кількості помилок.
III. Формулювання мети і завдань уроку
На цьому етапі уроку вчитель нагадує учням про те, що під час розв'язування задач на чотирикутники часто доводиться мати справу із трикутниками (див. попередній урок).
Серед усіх видів трикутників, що були вивчені на попередніх уроках геометрії, на особливу увагу заслуговує прямокутний трикутник із гострим кутом 30° (яку властивість має такий трикутник?). Отже, основне питання полягає в тому, щоб, пригадавши властивість вище названого трикутника та вивчені на попередніх уроках властивості трапецій, сформувати вміння застосовувати ці твердження під час розв'язування задач на трапецію (там, де це можливо).
IV. Актуалізація опорних знань
Для свідомого розуміння та подальшого оволодіння учнями способами дій, опрацьованих на уроці, слід активізувати знання і вміння учнів щодо властивостей гострих кутів прямокутного трикутника; властивості катета, що лежить проти кута 30°; властивостей кутів, діагоналей, висоти рівнобічної трапеції.
Виконання усних вправ
- Скільки кутів трикутника мають бути відомими, щоб можна було визначити решту кутів цього трикутника? Розгляньте випадки:
1) довільний трикутник;
2) прямокутний трикутник;
3) рівнобедрений трикутник;
4) рівносторонній трикутник;
5) прямокутний рівнобедрений трикутник.
- Відомо, що коли в трикутнику один кут прямий, то два інші — гострі. А чи правильне обернене твердження?
- Яким — гострокутним, прямокутним чи тупокутним — є трикутник, коли:
1) один із його кутів дорівнює сумі двох інших;один із його кутів більший
 2) від суми двох інших;
2) від суми двох інших;
3) один із його кутів менший від суми двох інших?
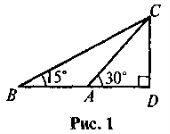
- Дано: CDLBD, CD = 100 (рис. 1). Знайдіть АВ.
VI. Формування вмінь, відпрацювання навичок
Ha уроці в неявному вигляді учням подається до вивчення так званий метод допоміжного трикутника (досить широко використовується в розв'язуванні різного виду задач) і вводиться прийом, який полягає в тому, що знаходження елементів трапеції здійснюється через використання властивостей трикутника, який є в складі цієї трапеції та має з нею спільні елементи. Оскільки учні поки що мають досить обмежені можливості щодо розв'язування трикутників, то в задачах цього уроку використовуються тільки співвідношення для гострих кутів прямокутного трикутника, а також властивість катета, що лежить проти кута 30°.
* Метод допоміжного трикутника використовується і під час розв'язування задач на побудову (зокрема на побудову трапеції). Оскільки вміння розв'язувати задачі на побудову трапеції (паралелограмів) не є обов'язковим, то питання про способи побудови паралелограмів та трапеції вивчається лише в тому випадку, коли для цього є умови (учні добре засвоїли матеріал на попередніх уроках, оволоділи способами розв'язання задач на обчислення й доведення). У цьому випадку на уроці, ознайомивши учнів із методом допоміжного трикутника, можна показати способи його застосування під час розв'язування задач на побудову трапецій (паралелограмів).
Формування вмінь застосовувати властивості трапеції разом із вивченими властивостями прямокутних трикутників (у тому числі й властивістю катета, що лежить проти кута 30°) логічно було б розпочати з розгляду випадків утворення трикутників під час розв'язування задач на трапецію.
Пропонуємо учням розглянути рис. 2 та за рисунком виконати завдання:
- дати опис фігури, що зображена на рисунку;
- назвати властивості трикутника, що заштрихований на рисунку (у кожному випадку).
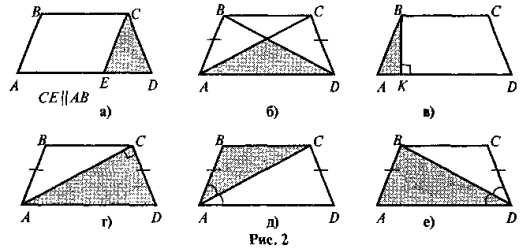
Після виконання усного завдання учні мають усвідомити зв'язок між елементами трапеції певного виду та видом трикутника, через елементи якого визначаються шукані елементи трапеції, та зафіксувати їх як «типові додаткові побудови для трапеції» (див. Геометрія в таблицях, Є. П. Нелін, с. 18).
Далі вже слід приступити до розв'язування конкретних задач.
Виконання усних вправ за готовими рисунками
|
1 |
|
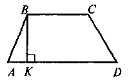
Дано: ABCD — трапеція, ВК
Знайти: кути трапеції |
|
2 |
|
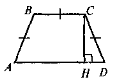
Дано: ABCD — трапеція, AB = BC = CD = а,
СН Знайти: AD |
|
3 |
|
Дано: ABCD – трапеція, Знайти: AD |
Виконання письмових вправ
-
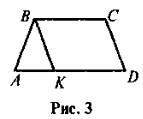 У трапеції ABCD через вершину В проведено пряму ВК, паралельну стороні CD (рис. 3).
У трапеції ABCD через вершину В проведено пряму ВК, паралельну стороні CD (рис. 3).
а) Доведіть, що KBCD — паралелограм.
б) Знайдіть периметр трапеції, якщо ВС = 4 см,
PΔABK = 11см.
- Діагональ рівнобедреної трапеції ділить навпіл її гострий кут, який дорівнює 60°. Знайдіть периметр трапеції, якщо її менша основа дорівнює 15 см.
- Один з гострих кутів рівнобічної трапеції дорівнює 60°, а довжина бічної сторони — 16 см. Знайдіть основи трапеції, якщо їх сума дорівнює 38 см.
- Бісектриса рівнобічної трапеції, проведена з вершини тупого кута, паралельна бічній стороні. Обчисліть основи трапеції, якщо її периметр дорівнює 60 см, а бічна сторона — 14 см.
- Більша основа рівнобічної трапеції дорівнює 18 м, а її діагональ є бісектрисою гострого кута трапеції. Знайдіть меншу основу трапеції, якщо її периметр 54 см.
-
 Діагональ рівнобічної трапеції є бісектрисою тупого кута, а її основи дорівнюють 8 см і 14 см. Знайдіть периметр трапеції.
Діагональ рівнобічної трапеції є бісектрисою тупого кута, а її основи дорівнюють 8 см і 14 см. Знайдіть периметр трапеції.
-
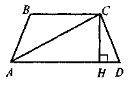
Відрізок EF трапеції ABCD (рис. 4) паралельний стороні CD, а точка Е — середина АВ. Доведіть, що EF =
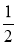 CD.
CD.
- Побудуйте паралелограм за двома сторонами й діагоналлю.
- Побудуйте паралелограм за стороною, діагоналлю і кутом, протилежним до цієї діагоналі.
VII. Підсумки уроку
Учні мають усвідомити, що знання властивостей трикутників є підґрунтям не лише для доведення теорем. Використання властивостей трикутників є також засобом розв'язування задач, в умові яких йде мова про інші геометричні фігури.
VIII. Домашнє завдання
Повторити зміст теоретичного матеріалу. Розв'язати задачі.
- Середина більшої основи рівнобедреної трапеції сполучена з вершинами меншої основи. При цьому утворилися три рівносторонні трикутники.
а) Знайдіть кути трапеції.
б) Знайдіть периметр трапеції, якщо периметр одного трикутника дорівнює 12 м.
- Довжини бічних сторін трапеції дорівнюють 2а, а довжини основ — 7а і 9а. Знайдіть кути трапеції.
- Більша основа рівнобічної трапеції дорівнює 12 см, а бічна сторона — 4 см. Гострий кут трапеції дорівнює 60°. Знайдіть меншу основу трапеції.
- У рівнобічній трапеції з тупим кутом 120° через вершину тупого кута проведено пряму, яка паралельна бічній стороні і відтинає від більшої основи відрізок довжиною 12 см. Знайдіть периметр трапеції, якщо менша основа дорівнює 16 см.


про публікацію авторської розробки
Додати розробку