Означення трапеції. Окремі види трапецій
Тема. Означення трапеції. Окремі види трапецій
Мета: сформувати в учнів поняття трапеції, її елементів; розглянути означення рівнобічної та прямокутної трапецій, зміст властивостей кутів трапеції, прилеглих до бічної сторони, та кутів рівнобічної трапеції.
Формувати вміння:
- відтворювати вивчені твердження;
- виконувати рисунок за описом;
- за готовим рисунком знаходити елементи трапеції;
- розв'язувати найпростіші задачі на обчислення.
Тип уроку: засвоєння нових знань.
Наочність та обладнання: конспект «Трапеція. Види трапеції».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Учитель збирає зошити учнів із виконаним аналізом контрольної роботи.
III. Формулювання мети і завдань уроку
З метою створення позитивної мотивації навчальної діяльності учнів та формування розуміння логіки вивчення матеріалу можна звернутися до схеми, складеної на уроці № 10.
За цією схемою пропонуємо учням, користуючись раніше набутими знаннями, відповісти на запитання.
- Яка фігура називається чотирикутником?
- Яку додаткову умову треба знати, щоб стверджувати, що поданий чотирикутник є паралелограмом?
- Чи правильно, що будь-який чотирикутник є паралелограмом?
-
Чи є паралелограмом чотирикутник, тільки дві протилежні сторони якого паралельні? Виконайте зображення такого чотирикутника. Відповідаючи на запитання, учні мають дійти усвідомлення того факту, що:
- паралелограми (вивчені на попередніх уроках) є лише одним із принаймні двох видів опуклих чотирикутників;
- окрім паралелограмів (які мають дві пари паралельних сторін), існують чотирикутники, у яких лише одна пара паралельних сторін.
Таким чином, виділяється новий геометричний об'єкт. Увести означення цієї фігури, розглянути її властивості, види — основна мета уроку.
IV. Актуалізація опорних знань
 З метою свідомого розуміння та подальшого засвоєння учнями змісту означення, властивостей та ознак рівнобічної трапеції слід активізувати знання і вміння щодо ознак та властивостей паралельних прямих (перетнуті третьою), ознак рівності прямокутних трикутників, визначення відстані між паралельними прямими (див. 7 клас), а також означення чотирикутника.
З метою свідомого розуміння та подальшого засвоєння учнями змісту означення, властивостей та ознак рівнобічної трапеції слід активізувати знання і вміння щодо ознак та властивостей паралельних прямих (перетнуті третьою), ознак рівності прямокутних трикутників, визначення відстані між паралельними прямими (див. 7 клас), а також означення чотирикутника.
Виконання усних вправ
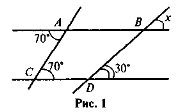
- За. рисунком 1 знайдіть кут х.
- Про три точки відомо, що вони знаходяться на однаковій відстані від однієї й тієї ж прямої. Чи можна стверджувати, що вони лежать на одній прямій?
- Як накреслити дві паралельні прямі на відстані 3 см одна від одної?
-
На рисунку 2 АВ || DE. Доведіть, що
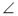 ABС +
ABС + 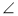 BCD +
BCD + 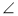 СDE = 360°.
СDE = 360°.
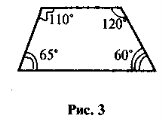
- Чи правильно виконано рисунок 3?

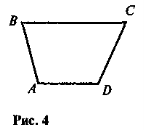
-
На рисунку 4 AD || ВС. Доведіть, що
 С +
С +  D = 180°.
D = 180°.
V. Засвоєння знань
План вивчення нового матеріалу
- Означення трапеції. Елементи трапеції (основи, бічні сторони, кути, висоти).
- Властивості кутів трапеції, прилеглих до бічних сторін; висот трапеції.
- Прямокутна трапеція: означення, властивість висот прямокутної трапеції.
- Рівнобічна трапеція: означення, властивості кутів та діагоналей, ознаки рівнобічної трапеції.
Якщо порівнювати зміст та послідовність вивчення матеріалу за новим підручником та за підручником, який було рекомендовано використовувати раніше (див. Геометрія. 7-9, О. В. Погорєлов), то помітна суттєва відмінність як у послідовності, так і в змісті пропонованого навчального матеріалу. А саме: в новому підручнику спочатку пропонується вивчити поняття трапеції та її види, а вже після цього вивчається теорема Фалеса та її застосування під час обчислення середньої лінії трикутника і трапеції. Така послідовність вивчення сприяє формуванню в учнів цілісного уявлення про поняття чотирикутника: більш логічно вивчивши поняття чотирикутника на виділивши один із його видів (із двома парами паралельних сторін), розглянути інший можливий випадок (з однією парою паралельних сторін). А вже далі більш поглиблено вивчити особливі властивості кожного з виділених видів чотирикутників.
Якщо порівнювати зміст матеріалу, то в новому підручнику він суттєво розширений за рахунок уведення в текст властивості кутів при бічних сторонах трапеції, властивості висот трапеції, виділення двох видів (прямокутної та рівнобічної) трапеції та уведення поняття ознаки рівнобічної трапеції (за кутами та при основі)- Оскільки зміст матеріалу, запропонованого у підручнику, майже повністю відповідає плану вивчення теми, то вивчення нового матеріалу на уроці можна організувати як самостійну роботу учнів із здобуття знань.
Залежно від рівня навчальних досягнень учнів класу та за наявності часу можна розглянути такі твердження (із доведенням):
- висота прямокутної трапеції дорівнює одній з її бічних сторін;
- діагоналі рівнобічної трапеції рівні, і навпаки, якщо діагоналі трапеції рівні, то вона рівнобічна;
- сума протилежних кутів рівнобічної трапеції дорівнює 180°;
- діагоналі рівнобічної трапеції утворюють з її основою рівні кути, і навпаки, якщо діагоналі трапеції утворюють з її основою рівні кути, то трапеція рівнобічна;
-
висота рівнобічної трапеції, що проведені з вершини тупого
кута, ділить більшу з основ на відрізки, один з яких дорівнює
півсумі основ, а другий — піврізниці основ.
Оскільки об'єм нового матеріалу в темі «Трапеція. Види трапецій» є достатньо великим, то, залежно від рівня математичної підготовки учнів, планування вивчення розділу може бути різним: новий матеріал можна викласти на цьому уроці, тоді на наступному уроці буде відпрацьовано його застосування; або ж на цьому уроці вивчити тільки зміст матеріалу підручника та закріпити знання учнів щодо його змісту, а на наступному уроці доповнити знання учнів додатковими властивостями та ознаками (див. вище) та відпрацювати навички застосування всіх тверджень, вивчених у темі «Трапеція. Види трапецій».
Повний зміст навчального матеріалу уроку міститься в конспекті «Трапеція. Види трапецій».
|
Конспект 5 |
||
|
Трапеція. Види трапецій |
||
|
|
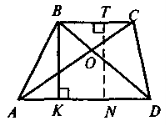
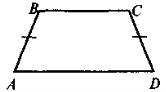
Означення. Чотирикутник, дві сторони якого паралельні, а дві інші непаралельні, називається трапецією
АС і BD — діагоналі, ВК і TN — висоти |
|
|
|
Властивості Якщо ABCD — трапеція, основи ВС і AD, висоти ВК і TN, то:
1) 2) ВК = ТN |
|
|
|
Окремі випадки трапеції |
|
|
|
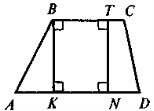
а) Означення. Трапеція, одна з бічних сторін якої перпендикулярна до основ, називається прямокутною
|
|
|
|
Властивості
Якщо в трапеції ABCD BC || AD і |
|
|
|
б) Означення. Трапеція з рівними бічними сторонами називається рівнобічною трапецією
|
|
|
|
Властивості |
Ознаки |
|
|
1) Якщо ABCD — рівнобічна трапеція з основами ВС і AD, то
а)
б) в) AС = BD
г) |
1) Якщо в трапеції ABCD BC || AD, ABCD — рівнобічна трапеція |
|
|
2) Якщо ABCD — рівнобічна трапеція. BC || AD, AB = CD i |
2) Якщо в трапеції ABCD BC || AD і AC = BD то ABCD — рівнобічна трапеція |
|
|
3) Якщо ABCD — рівнобічна трапеція, BC || AD і CD = AD |
3) Якщо в трапеції ABCD BC || AD
і ABCD — рівнобічна трапеція |
VI. Формування первинних умінь Виконання усних вправ
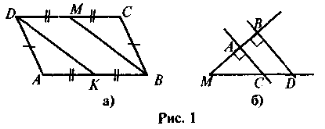
- Знайдіть на рисунку 1 трапеції. Назвіть їх основи й бічні сторони.
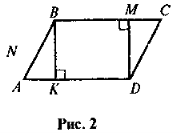
- ABCD — паралелограм (рис. 2). Скільки ще чотирикутників ви бачите на рисунку? Чи є серед них паралелограми; трапеції?
- Чи можуть основи трапеції дорівнювати одна одній? Чому?
- Чи можуть сусідні кути трапеції бути рівними? Чи можуть протилежні кути трапеції бути рівними?
- Чи обов'язково кути трапеції, прилеглі до більшої основи, є гострими? Наведіть приклади.
- Чи може рівнобічна трапеція бути прямокутною?
- Чи може висота трапеції бути більшою за бічну сторону? дорівнювати бічній стороні?
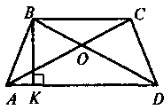
- Діагоналі трапеції ABCD (BC || AD) перетинаються в точці О.
а) Чи може трикутник AOD дорівнювати трикутнику ВОС?
б) Чи може трикутник АОВ дорівнювати трикутнику DOC?
- Чи може точка перетину діагоналей трапеції бути серединою кожної з них; однієї з них?
Особливу увагу слід звернути на вправу № 3. Крім попередження типової помилки учнів (основи трапеції нерівні), це завдання має на меті повідомити учням про найпоширеніший спосіб зображення довільної трапеції: спочатку зображують два нерівних паралельних відрізки, а потім їх кінці з'єднують двома іншими відрізками.
Виконання графічних вправ
- Накресліть паралелограм ABCD і проведіть у ньому висоту СН.
а) Визначте вид трапеції АВСН.
б) Чи є висотою трапеції будь-яка висота паралелограма? Наведіть контрприклад.
-
Накресліть рівнобедрений трикутник AMD з основою AD. Позначте
на стороні AM точку В і проведіть через неї пряму, паралельну AD.
Позначте точку С — точку перетину цієї прямої зі стороною МD.
а) Визначте вид трапеції ABCD.
б) Проведіть діагоналі трапеції. Виміряйте і порівняйте їх довжини.
Виконання письмових вправ
- У рівнобедреній трапеції висота, проведена з вершини тупого кута, ділить більшу основу на відрізки завдовжки 6 см і ЗО см. Знайдіть меншу основу трапеції.
- Знайдіть невідомі кути:
а) трапеції ABCD з основами AD і ВС, якщо ![]() A = 40°,
A = 40°, ![]() D = 50°;
D = 50°;
б) рівнобедреної трапеції, один із кутів якої дорівнює 58°;
в) прямокутної трапеції, найбільший кут якої утричі більший за найменший.
VII. Підсумки уроку
- Чи можуть довжини основ трапеції бути рівними?
- Чи може основа трапеції дорівнювати бічній стороні?
- Чи можуть бути рівними кути трапеції, що прилеглі до бічної сторони?
- Які спільні властивості мають трапеція і паралелограм?
- Чи існує трапеція, в якій: а) два протилежні кути рівні; б) три кути гострі?
- Чи може сума кутів при меншій основі трапеції бути більшою за суму кутів при більшій основі?
VIII. Домашнє завдання
Вивчити зміст означень, теорем та їх доведення. Розв'язати задачі.
- Знайдіть невідомі кути:
а) рівнобедреної трапеції, висота якої, проведена з вершини тупого
кута, утворює з бічною стороною кут 22°;
б) прямокутної трапеції, яку діагональ, проведена з вершини тупого кута, ділить на два рівнобедрені прямокутні трикутники.
- Менша основа рівнобедреної трапеції дорівнює 10 см. Знайдіть більшу основу трапеції, якщо висота, проведена з вершини тупого кута, ділить її на відрізки, один з яких дорівнює 3 см.
-
O — точка перетину бісектрис кутів А і В трапеції ABCD (рис. 3). Доведіть, що
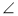 AOB = 90°.
AOB = 90°.


про публікацію авторської розробки
Додати розробку