Окремі види трапецій та їх властивості
Тема. Окремі види трапецій та їх властивості
Мета: доповнити знання учнів властивостями та ознаками окремих видів трапецій і домогтися засвоєння змісту вивчених тверджень; сформувати вміння відтворювати вивчені властивості та ознаки окремих видів трапецій, а також використовувати їх у здійсненні послідовних міркувань під час розв'язування задач.
Тип уроку: застосування знань, умінь та навичок.
Наочність та обладнання: конспект «Трапеція. Види трапеції».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Традиційно для перевірки засвоєння учнями змісту означень та властивостей трапеції та її окремих видів проводиться математичний диктант.
Математичний диктант
Варіант 1
- Чи є трапецією будь-який чотирикутник, у якому є дві паралельні сторони?
- Сторони кута (нерозгорнутого) перетнуті двома паралельними прямими. Який чотирикутник утворився?
- У трапеції MNPK MN || PK.
а) Назвіть основи і бічні сторони трапеції.
б) Чому дорівнює сума ![]() M +
M +![]() P?
P?
в) Чи може виконуватись рівність MN = РК?
г) Чи може виконуватись рівність NP = MK? Відповідь поясніть.
д) Якщо NP = МК, то якими будуть відрізки MP і NK?
Варіант 2
- У чотирикутнику ABCD сторони АВ і CD не паралельні. Чи обов'язково цей чотирикутник є трапецією?
- Дві паралельні прямі перетнуті двома прямими, що мають спільну точку. Як називається чотирикутник, що утворився?
- У трапеції ABKFBK не паралельна AF.
а) Назвіть основи й бічні сторони трапеції.
б) Чому дорівнює сума ![]() A +
A +![]() F?
F?
в) Чи може виконуватись рівність ![]() A =
A =![]() F? Якщо так, то в якому випадку?
F? Якщо так, то в якому випадку?
г) Чи може виконуватись рівність BF = АК? Якщо так, то в якому випадку?
д) Якщо AF = ВК, то що можна сказати про куги В і F?
Правильність виконання домашніх вправ достатньо перевірити під час фронтальної бесіди. Задача № 3 дає учням формулювання властивостей бісектрис кутів трапеції, прилеглих до бічної сторони, тому її доведення слід обговорити, а опорний факт зафіксувати. (Розв'язання цієї задачі заздалегідь за дошкою може виконати сам учитель або доручити це одному із «сильних» учнів).
III. Формулювання мети і завдань уроку
Якщо на попередньому уроці не були вивчені всі властивості рівнобічної трапеції (включаючи додаткові властивості діагоналей, кутів між діагоналями та основами тощо), то для формулювання мети достатньо буде слів учителя про те, що рівнобічна трапеція, крім указаних у тексті підручника властивостей та ознаки, має ще ряд цікавих критеріїв, тобто властивостей та обернених ознак; тому метою уроку є вивчення (тобто ознайомлення зі змістом, доведення та запам'ятовування) цих додаткових властивостей та ознак, а також оволодіння способами їх застосування під час розв'язування задач.
IV. Актуалізація опорних знань
З метою свідомого розуміння та подальшого засвоєння учнями змісту властивостей та ознак рівнобічної трапеції слід активізувати знання і вміння учнів щодо означення трапеції та визначення її елементів на готовому зображенні та за позначенням трапеції; визначення окремих видів трапецій; вивчених властивостей трапеції загального виду та окремих видів трапецій; означення, властивостей та ознак рівнобедреного трикутника, прямокутного трикутника, рівностороннього трикутника.
Виконання усних вправ за готовими рисунками
|
1 |
|
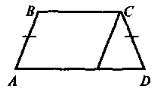
Дано: ABCD — рівнобічна трапеція.
Довести: |
|
2 |
|
Дано: ABCD — рівнобічна трапеція. Довести: АС = BD |
|
3 |
|
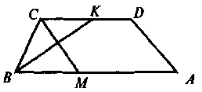
Дано: ABCD — трапеція, ВК — бісектриса кута В, CM — бісектриса кута С
Довести: СМ |
|
4 |
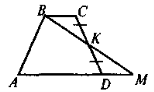
|
ABCD – трапеція, СК = KD. Довести: ВС = DM |
|
5 |
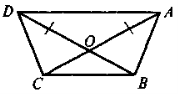
|
Дано: АВСD — трапеція, АО = ОD. Довести: AB = DC |
|
6 |
|
Дано: ABCD – трапеція,
Знайдіть кути трапеції ABCD |
V. Доповнення знань
План вивчення нового матеріалу
- Властивість діагоналей рівнобічної трапеції. Ознака рівнобічної трапеції за діагоналями (опорна задача).
- Властивість кутів, утворених діагоналями рівнобічної трапеції з її основою. Ознака рівнобічної трапеції за кутами, утвореними діагоналями з однією з основ (опорна задача).
3*. Властивість рівнобічної трапеції, діагональ якої є бісектрисою:
- гострого кута;
- тупого кута.
4. Властивість відрізків, на які ділить більшу основу висота рівнобічної трапеції, що проведена з вершини тупого куга.
Матеріал, винесений для вивчення на уроці, віднесено до додаткового матеріалу (або взагалі може розглядатися тільки на конкретному прикладі). Але автор вважає, що з метою успішного вивчення геометрії в середній школі знання названих властивостей корисні для учнів (тим більше, що доведення цих тверджень є досить простими і спираються на матеріал, добре опрацьований учнями у 7 класі, — ознаки рівності трикутників та означення й ознаки рівнобедреного трикутника). Інша річ, вивчення критеріїв рівнобічної трапеції. Якщо учні мають високий рівень інтелектуальної активності, тоді їм можна запропонувати виконати доведення цих тверджень самостійно. В інших випадках доречно провести доведення названих тверджень у формі евристичної бесіди (для економії часу достатньо буде зафіксувати формулювання цих тверджень у зошитах і не вимагати від учнів відтворення доведення) або організувати роботу в малих групах (кожна група отримує для доведення певну властивість) із наступною презентацією та фіксацією в зошитах учнів формулювань тверджень.
VI. Формування первинних умінь
Виконання усних вправ
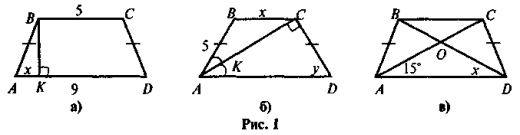
Знайдіть х, у (рис. 1).
VII. Засвоєння вмінь та навичок
Виконання письмових вправ
- Знайдіть кути:
а) рівнобічної трапеції, якщо різниця двох її протилежних кутів дорівнює 80°;
б) прямокутної трапеції, діагональ якої є бісектрисою тупого кута
й утворює з меншою бічною стороною кут 35°.
- Менша основа рівнобічної трапеції дорівнює бічній стороні, а діагоналі перпендикулярні до бічних сторін. Знайдіть кути трапеції.
- У трапеції ABCD точка О — точка перетину діагоналей. Відрізки ОА і OD рівні. Доведіть, що АВ = СD.
-
Висота рівнобічної трапеції, що проведена з вершини тупого кута,
ділить більшу основу трапеції на відрізки довжиною 3 см і 11 см.
Знайдіть основи трапеції. - Діагональ рівнобічної трапеції утворює з основою кут 32°, а її бічна сторона дорівнює меншій основі. Знайдіть кути трапеції.
VIII. Підсумки уроку
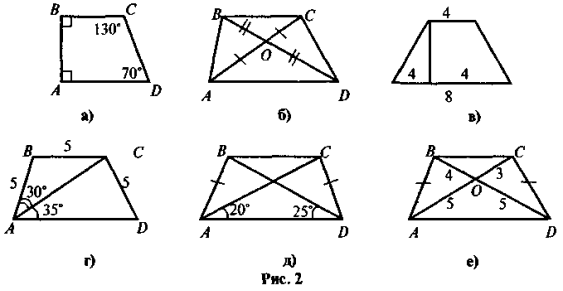
Якої помилки припустилися в зображенні трапеції на рис. 2?
IX. Домашнє завдання
Вивчити зміст означень, властивостей та ознак трапеції.
Розв'язати задачі.
- Знайдіть кути прямокутної трапеції, якщо відношення найбільшого і найменшого з них дорівнює 3 : 2.
- Діагональ рівнобедреної трапеції є бісектрисою її тупого кута. Знайдіть периметр трапеції, якщо її основи дорівнюють 5 см і 10 см. Повторити властивість катета, що лежить проти кута 30°.


про публікацію авторської розробки
Додати розробку