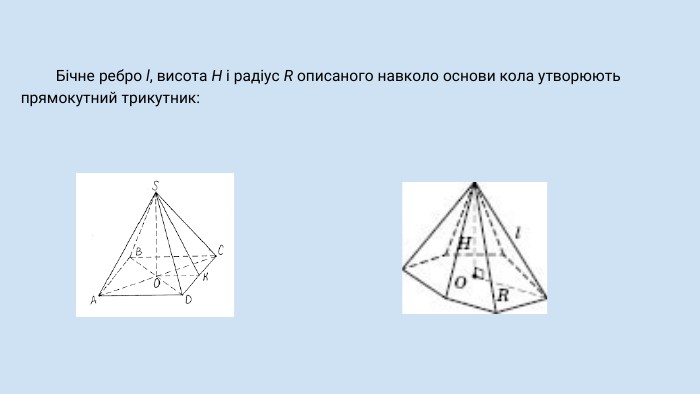
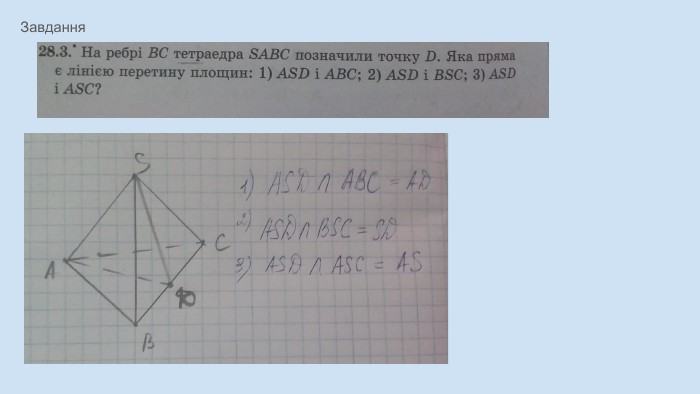
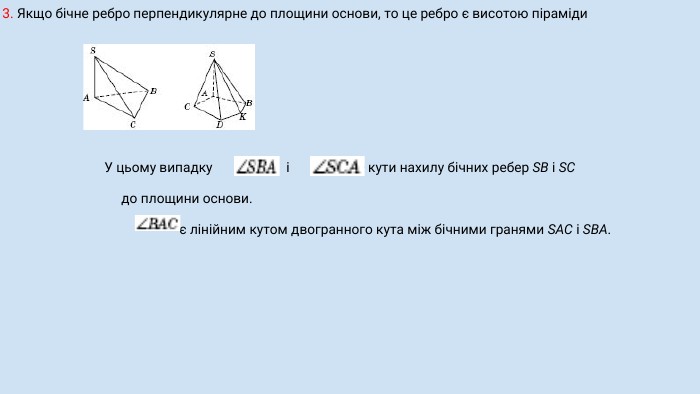
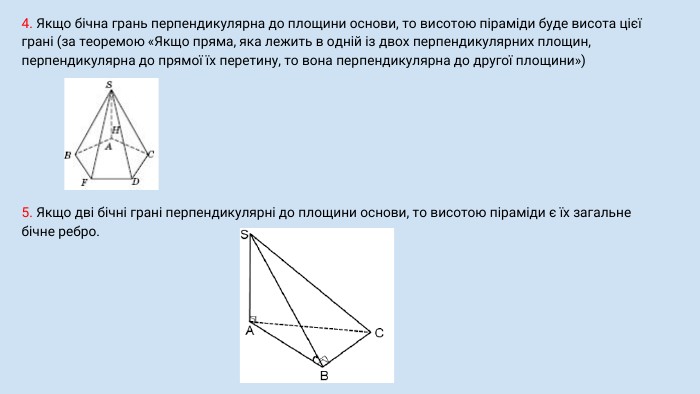
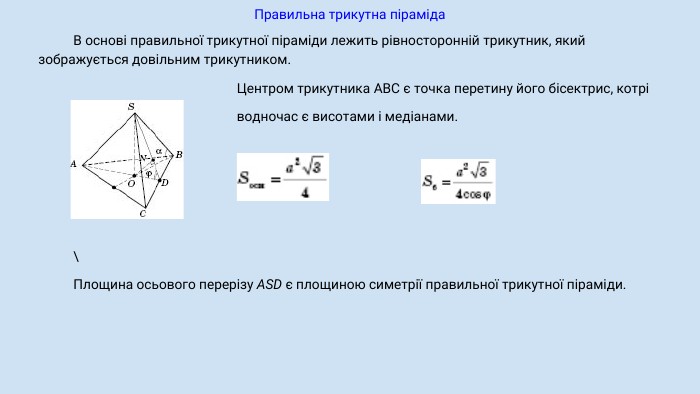
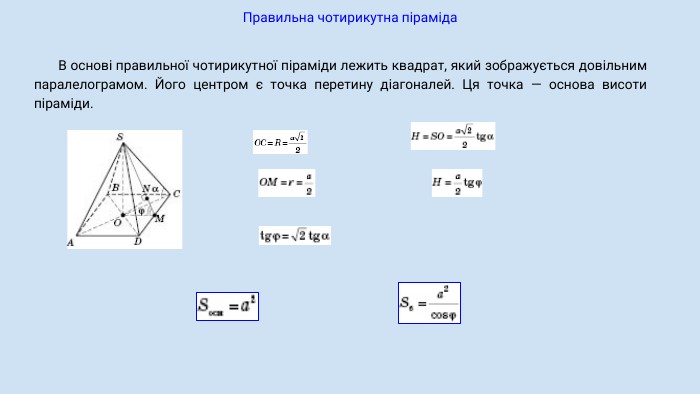
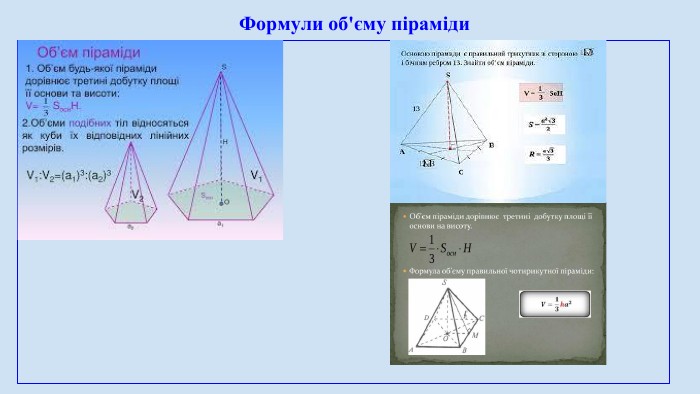
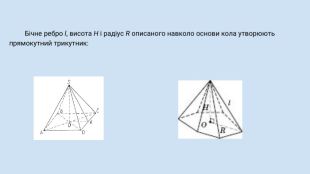
Піраміда, її види, властивості елементів. Формула об'єму.
Про матеріал
Методика вивчення многогранників.
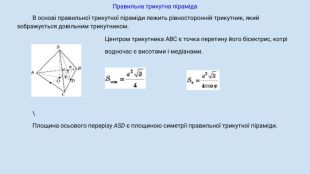
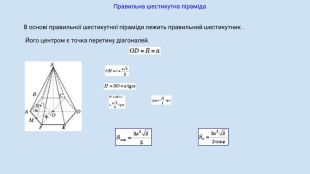
Піраміда, її види, властивості елементів.
Формула об'єму.
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку