Міністерство освіти та науки України

Департамент освіти і науки

Полтавської обласної військової адміністрації 

Вище професійне училище № 7

м. Кременчука Полтавської області

Н. Грудкова

МНОГОГРАННИКИ

Методична розробка з математики

                                                                                     Кременчук-2023                                        

Грудкова Н. Многогранники: методична розробка з математики, ВПУ № 7, м. Кременчук-2023, 27 с.

                                                                       Методист ВПУ №7

___________ Юлія ХАЙЧІНА

Розглянуто та схвалено до використання в освітньому процесі ВПУ №7 на засіданні циклової методичної комісії «Природничо-математична підготовка».

Протокол ____.____.2023 № __

Голова ЦМК _________ Людмила ТОКШЕЛУКОВА

 

АНОТАЦІЯ

У методичній розробці підсумкового уроку з математики (геометрія) «Многогранники» представлено методику проведення уроку-гри.

Мета уроку - узагальнити і систематизувати вивчений матеріал з теми «Многогранники», удосконалити вміння й навички застосування цих знань при розв’язуванні задач.

Для проведення уроку пропонується використання вправ: «Зашифровані поняття», «Острів геометричних фігур», «Розірвані речення», «П’ятнашки»,

«Підсумковий тест», що створено різними онлайн інструментами - Rebus 1, ThingLink, PurposeGames, Learningapps.

           

УРОК № ____

Тема програми № 4. Многогранники (14 год)

Тема уроку. Підсумковий урок з теми «Многогранники».

Тип уроку: урок корекції предметних компетентностей.

Вид уроку: урок-гра.

Цілі уроку:

-           корекція предметних компетентностей: узагальнити і систематизувати вивчений матеріал з теми «Многогранники», удосконалити вміння й навички застосовування цих знань при розв’язуванні задач;

-           розвиток ключових компетентностей:

-           математична компетентність – розвивати логічне мислення, просторову уяву, формувати вміння розв’язувати проблемні ситуації, знаходити раціональний шлях розв’язування задач, моделювати процеси та ситуації із застосуванням математичних формул та арифметичних операцій;

-           уміння вчитися впродовж життя – аналізувати, контролювати, корегувати та оцінювати результати власної навчальної

діяльності;

-           вільне володіння державною мовою: вміння висловлювати свої думки, чітко та аргументовано пояснювати математичні дії, оперувати математичними термінами;

-           інформаційно-комунікаційна компетентність: здатність безпечного та ефективного використання засобів та

інструментів діджитал-технологій у навчанні;

-           громадянські та соціальні компетентності: співпраця з одногрупниками для досягнення спільної мети, дотримування загальноприйнятих правил поведінки, керувати власними емоціями.

Методична мета: продемонструвати методику використання ігрових форм навчання під час проведення уроку корекції предметних компетентностей.

Очікувані результати: учень/учениця:

-           розпізнає та зображує основні види многогранників та їх елементи;

-           має уявлення про перерізи многогранника площиною;

-           формулює означення вказаних у змісті многогранників;

-           записує формули для обчислення площі бічної та повної поверхонь призми та піраміди, формули їх об’ємів;

-           застосовує вивчені формули і властивості до розв’язування задач, зокрема прикладного змісту.

Забезпечення:

-           дидактичне: Істер О.С. Математика: (алгебра і початки аналізу та геометрія, рівень стандарту): підруч. для 11-го кл. закл. заг. серед. освіти / Олександр Істер. - Київ: Генеза, 2019. - 304 с. -: іл; інфографіка

«Многогранники: основні аспекти», презентація викладача «Многогранники: підсумковий урок»; тематичний сайт викладача

«Піраміди»; задачник, відеоколекція «Многогранники»;

-           програмне: Rebus 1, ThingLink, PurposeGames, Learningapps, Canva, MS PowerPoint; Google Classroom;

-           матеріально-технічне: ноутбук, мультимедійний проєктор, дошка, крейда, креслярське приладдя, смартфони учнів.

Міжпредметні зв’язки: історія, географія, хімія, інформатика, українська мова.

Епіграф: «Правильних многогранників надзвичайно мало, але цей дуже скромний за кількістю загін зумів пробитись у найбільші глибини різних наук».

Льюїс Керрол 

           

ХІД УРОКУ

І. Організаційний момент (1 хв.)

ІІ. Орієнтація, мотивація (5 хв.)

2.1. Аналіз контрольної роботи

2.2. Повідомлення теми та завдання уроку

2.3. Мотивація до співпраці

ІІІ. Цілепокладання (10 хв.)

3.1. Математична зарядка

3.1.1. Зашифровані поняття

3.1.2. Острів геометричних фігур

3.1.3. Розірвані речення

3.2. Многогранники: важливі аспекти (випереджувальне завдання)

ІV. Цілереалізація (23 хв.)

V. Цінування. Оцінювання (5 хв.)

5.1. Підсумковий тест

5.2. Аналіз діяльності учнів на уроці

VІ. Повідомлення домашнього завдання, роз’яснення етапів його виконання (1 хв.)

           

ПЕРЕБІГ УРОКУ

І. ОРГАНІЗАЦІЙНИЙ МОМЕНТ

Етап зорієнтований на перехід від режиму паузи до режиму навчання.

Мета: мобілізувати учнів, з’ясувати ступінь готовності учнів до уроку.

Методичний коментар. На початку уроку відбувається організаційний момент, що забезпечить свідому підготовку учнів до активної колективної взаємодії: привітання, перевірка готовності учнів до уроку. Викладач наголошує на принципах роботи на уроці. 

Принципи роботи на уроці

Принцип 1. Поважай думки своїх одногрупників, не насміхайся, критикуй толерантно.

Принцип 2. Зусилля кожного учня потрібні і незамінні для успіху всієї групи.

ІІ. ОРІЄНТАЦІЯ, МОТИВАЦІЯ

Етап зорієнтований на підготовку до активної взаємодії, аналіз тематичного зрізу знань.

Мета: сформувати позитивні мотиви корекції предметної компетентності та розвитку ключових компетентностей.

2.1. Аналіз контрольної роботи

Методичний _{коментар}. На попередньому уроці учні виконували підсумкову контрольну роботу, оцінки за яку вони переглянули в електронному журналі. Викладач робить загальний підсумок виконання контрольної роботи, акцентуючи увагу на типових помилках.

При виконанні контрольної роботи найбільш складною виявилася задача з параметрами на обчислення площі повної поверхня піраміди. Помилки також були допущені у формулах: радіусу вписаного кола в правильний трикутник; площі повної поверхні прямокутного паралелепіпеда. Все це привело до неправильного розв’язуння задач. 

2.2. Повідомлення теми та завдання уроку

Методичний коментар. Повідомляється тема уроку, формуються завдання.

2.3. Мотивація до співпраці

Прийоми: мотивуюча розповідь, використання яскравої цитати.

Форми: фронтальна.

Засоби: презентація викладача «Многогранники: підсумковий урок».

Методичний коментар. Із метою забезпечення візуалізації уроку використовується презентація викладача «Многогранники: підсумковий урок». Це дозволяє візуалізувати інформаційний контент, заощадити час та задіяти в роботі всі психофізіологічні тригери учнів.

Мотивація важлива на кожному етапі вивчення математики, оскільки це допомагає учням зберегти інтерес і бажання навчатися. Мотиваційна розповідь допоможе підкреслити важливість математики для побудови майбутньої освітньої траєкторії.

Людина проявляє інтерес до многогранників та многокутників протягом усього свого життя – від дворічної дитини, що бавиться дерев'яними кубиками, до зрілого математика. Це пов'язано з красою і досконалістю форм, які досить часто зустрічаються в природі.

Математика є необхідною навичкою в багатьох сферах життя. Для досягнення успіху в майбутньому важливо розвивати математичну грамотність.

Поняття многогранника є одним із центральних у розділі стереометрії. Многогранники дають особливо багатий матеріал для розвитку поєднання живої просторової уяви із строгою логікою, яка складає суть геометрії.

             Хочеться     почати     урок    словами     Льюїса     Керрола:     «Правильних

многогранників надзвичайно мало, але цей дуже скромний за кількістю загін зумів пробитись у найбільші глибини різних наук».

На сьогоднішньому уроці ми повторимо особливості виконання практичних завдань з теми «Многогранники», так як ця тема є обов’язковою у виконанні завдань під час проходження НМТ.

ІІІ. ЦІЛЕПОКЛАДАННЯ

Етап зорієнтований на забезпечення спрямованості та орієнтації на предмет вивчення.

Мета - створення атмосфери підтримки та позитивних очікувань.

Вправи: «Зашифровані поняття», вправи-тренажери «Острів геометричних фігур», математичний пазл «Острів геометричних фігур», віртуальна дошка «Розірвані речення», випереджувальне завдання.

Форми: фокус-групи, індивідуальна, ланцюжок.

Засоби:картки-завдання з ребусами, онлайн-вправи, інфографіка «Многогранники: важливі аспекти», ноутбук, проєктор, біла дошка, презентація викладача.

3.1. Математична зарядка

Методичний коментар. На етапі цілепокладання необхідно створити атмосферу підтримки та позитивних очікувань, де помилки розглядаються як можливість для вдосконалення і розвитку. Математика - це не тільки навички, але і інструмент для розв'язання складних завдань та досягнення цілей у житті. Саме тому важливо створити відчуття цікавості, щоб учні мали бажання досліджувати світ математики.

3.1.1. Зашифровані поняття

Методичний коментар. Ребуси - чудова розумова гімнастика для активізації учнів на початку уроку. Вони розвивають і тренують пам’ять, загострюють догадливість, виробляють настирливість, здатність логічно думати, аналізувати, порівнювати, виробляти вміння орієнтуватись у власному словниковому запасі.

Для формування зацікавленості використовується прийом «Зашифровані поняття». Учням пропонується розгадати ребуси (робота у фокус-групах), у яких зашифровано ключові слові теми, та дати визначення відгаданих понять (таблиця 1). Для створення ребусів використано онлайн сервіс Rebus 1.

Таблиця 1 - Зашифровані поняття

Ребус	Очікувана відповідь
	МНОГОГРАННИК           Многогранник           -           це геометричне тіло, поверхня якого складається із скінченого числа плоских многокутників.
	ПРИЗМА Призма - це багатогранна об'ємна фігура, яка складається з двох однакових плоских багатокутників (основ), що знаходяться у двох паралельних площинах, а інші грані (бокові грані) - паралелограми, які мають спільні        сторони      з        цим багатокутником.
	ПІРАМІДА Піраміда - це тривимірна фігура з основою, яка є багатокутником, вершини якої стикаються в одній зовнішній точці.

 

           

3.1.2. Острів геометричних фігур

Методичний коментар. Із метою повторення геометричних фігур, учням треба було виконати вправи-тренажери (домашнє завдання), яку створено за допомогою сервісів ThingLink  та PurposeGames.

Для перевірки знань на уроці використовується математичний пазл «Острів геометричних фігур», створений за допомогою сервісу Learningapps.

Завдання представлено у таблиці 2.

Таблиця 2 - Острів геометричних фігур

Назва вправи	Посилання	QR-код
Вправа-тренажер «Острів геометричних фігур»: домашнє завдання	https://www.thinglink.com/scene/ 1300813791855902723
	https://www.purposegames.com/g ame/g2p4ZDSPR8B
Математичний пазл «Острів геометричних фігур» Завдання: скласти пазл, назвати фігуру, яка зображена на пазлі. Учні по черзі обирають фігури.	https://learningapps.org/watch?v= pdxtm1de323

 

           

3.1.3. Розірвані речення

Методичний коментар. Із метою повторення визначень, знання яких є основою для засвоєння теми, використовується вправа «Розірвані речення» (таблиця 3, додаток А), яка створена за допомогою сервісу Learningapps.

Таблиця 3 - Розірвані речення

Назва вправи	Завдання	Посилання / QR-код
Вправа «Розірвані речення»	Вправу починає викладач (керує вправою викладач): викладач читає початок речення, обирає учня, який закінчить речення. Цей учень обирає наступне речення та визначає наступного учня, який закінчить речення. Ланцюжок повторюється за заданою схемою. Після виконання вправи аналізується результат.	https://learningap ps.org/watch?v=p 64xbdc1t20

3.2. Многогранники: важливі аспекти

Методичний _{коментар}. Використання інфографіки на уроках математики допомагає візуалізувати математичні концепції та робить навчання більш цікавим і доступним для учнів. На попередньому уроці було видано індивідуальне випереджувальне завдання: підготувати інфографіку «Многогранники: важливі аспекти». Викладач аналізує виконану роботу та використовує інфографіку як роздатковий матеріал.

ІV. ЦІЛЕРЕАЛІЗАЦІЯ

Етап зорієнтований на корекцію та розвиток предметної компетентності учнів.

Мета - вироблення навичок і вмінь для розв’язування задач.

Вправи: гра «П’ятнашки», розв’язування задач, цікаві факти.

Форми: індивідуальна, фронтальна.

Засоби: ігрова панель, інфографіка «Многогранники: важливі аспекти», ноутбук, проєктор, біла дошка, презентація викладача, дошка, робочі зошити та учнівське приладдя.

Методичний коментар. На цьому етапі використовується гра «П’ятнашки». Ігрова панель містить номери завдань, за якими приховано практичні завдання та цікаві факти про многогранники. Завдання, що пропонуються, було включено до НМТ/ЗНО попередніх років. Учні обирають номер завдання і виконують його.

МАТЕМАТИЧНІ ЗАВДАННЯ

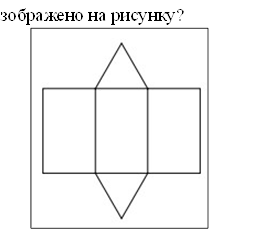
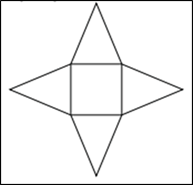ЗАВДАННЯ №1. Розгортку якого з наведених многогранників зображено на рисунку?

 

Варіанти відповіді:

А	Б	В	Г	Д

 

Очікувана відповідь: Б.

Маємо один чотирикутник - основу і 4 трикутника - бічні грані, тому наведено розгортку чотирикутної піраміди.

ЗАВДАННЯ №2. Визначте кількість граней восьмикутної піраміди.

Варіанти відповіді:

А	Б	В	Г	Д
7	8	9	16	17

 

Очікувана відповідь: В.

Маємо 8 бічних граней та 1 грань основи. Разом 9 граней.

ЗАВДАННЯ №3. Скільки всього граней у піраміди, яка має 12 ребер?

Варіанти відповіді:

А	Б	В	Г	Д
4	6	7	12	13

 

Очікувана відповідь: В.

Оскільки в піраміді однакова кількість бічних ребер та ребер основи, то дана піраміда має 12:2=6 ребер основи. Маємо 6 бічних граней та 1 грань основи. Разом 7 граней.

ЗАВДАННЯ №4. Сума довжин усіх ребер куба дорівнює 72 см. Визначте довжину одного ребра цього куба.

Варіанти відповіді:

А	Б	В	Г	Д
6 см	8 см	9 см	12 см	18 см

 

Очікувана відповідь: А. 

У куба всього 12 ребер. Тому довжина одного ребра 72:12=6 см.

ЗАВДАННЯ №5. Розгортку якого з наведених   многогранників зображено на рисунку?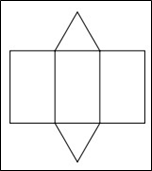

Варіанти відповіді:

А	Б	В	Г	Д

 

Очікувана відповідь: А.

Маємо два однакових трикутника - основи і 3  прямокутника - бічні грані, тому наведено розгортку трикутної призми.

 

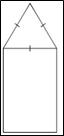ЗАВДАННЯ №6. На рисунку зображено прямокутник і трикутник, що є гранями правильної трикутної призми. Периметр цього прямокутника дорівнює 38 см. Визначте площу основи цієї призми, якщо довжина висоти призми дорівнює 11 см.

Варіанти відповіді:

А	Б	В	Г	Д
16      см2	32      см2	24 см2	64 см2	24      см2

 

Очікувана відповідь: А.

Оскільки маємо трикутну призму, то трикутник - це основа, а прямокутник - бічна грань призми. Тоді одна зі сторін прямокутника - висота довжиною 11 см, а друга - сторона основи. За формулою периметра прямокутника P=2(a+b) маємо: 38=2(а+11) а+11=38:2 а+11=19 a=8.

Площа основи S= см².

 

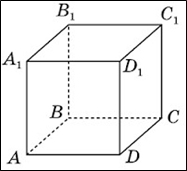ЗАВДАННЯ №7. На рисунку зображено куб ABCDA₁B₁C₁D₁. Визначте градусну міру кута між

прямими АВ₁ і DD₁.

Варіанти відповіді:

А	Б	В	Г	Д
0o	30o	45o	60o	90o

 

Очікувана відповідь: В.

Ці прямі лежать в паралельних площинах і не паралельні, тому вони мимобіжні. Кут між мимобіжними прямими дорівнює куту між прямими, що перетинаються і відповідно паралельні даним мимобіжним прямим. Оскільки

АА₁||DD₁, то кут між прямими АВ₁ і DD₁ дорівнює куту між прямими АВ₁ і АА₁. Оскільки ABCDA₁B₁C₁D₁ - куб, то AA₁B₁В - квадрат, а в квадраті кут між стороною та його діагоналлю дорівнює 45^o.

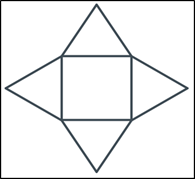
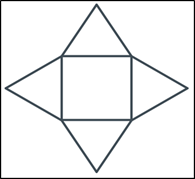ЗАВДАННЯ №8. На рисунку зображено розгортку піраміди, що складається з квадрата, сторона      якого дорівнює    10      см,     і         чотирьох правильних трикутників. Визначте площу бічної поверхні цієї піраміди.

 

Варіанти відповіді:

А	Б	В	Г	Д
100√3	100	400√3	100 ∙ (1 + √3)	200

 

Очікувана відповідь: А.

Оскільки дано піраміду з квадратом в основі і за умовою всі бічні грані – правильні трикутники, площу правильного трикутника можна знайти за формулою: 𝑆 , то площа бічної поверхні дорівнює:

𝑎

𝑆_б  

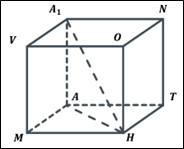
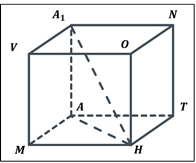ЗАВДАННЯ №9. Обчисліть площу бічної поверхні правильної чотирикутної призми, діагональ якої дорівнює 12 см і нахилена до площини основи під кутом 30°.

Дано:

MATHNOVA₁ − правильна призма

MATH −квадрат

A₁H = 12 см ∠A₁HA = 30°

Знайти:

S_б−?

Розв’язок:

Sб = Pосн ∙ AA1

Розглянемо ∆HAA₁:

                        ^{∠HAA1 = 90°}                                    проти кута 30° лежить катет

∠A1HA = 30°| ⇒ A1A = 6 см (вдвічі менший за гіпотенузу) A₁H = 12 см

AH см

Розглянемо квадрат MATH:

                                                                                                   AH     

MAсм

S_б см²

Відповідь: 𝟕𝟐√𝟔см^𝟐

ЦІКАВІ ФАКТИ

ФАКТ 1. Усі правильні многогранники були відомі в Стародавній Греції. Їм присвячена заключна 13-а книга знаменитих «Начал». Усього існує п'ять унікальних форм. Їх називають Платоновими тілами. Правильні многогранники по- грецьки закінчуються на едр (edrа-грань).

ФАКТ 2. Тетраедр - від «тетра» – чотири і грецького «hedra» – грань. Складається з 4-х правильних трикутників, в кожній його вершині сходяться 3 ребра. Сума плоских кутів при кожній вершині дорівнює 3ˣ60=180. Має 4 грані, 4 вершини і 6 ребер. Тетраедр символізував ВОГОНЬ, бо його вершина спрямована вгору.

ФАКТ 3. Гексаедр, від грецького «гекса» – шість і «hedra» - грань. Має шість квадратних граней, у кожній його вершині сходяться 3 ребра. Сума плоских кутів при кожній вершині дорівнює 3ˣ90=270. Має 6 граней, 8 вершин і 12 ребер. Гексаедр більш відомий як куб. Гексаедр - ЗЕМЛЯ, бо він «найстійкіший».

ФАКТ 4. Октаедр, від грецького «okto» - вісім і «hedra» - грань. Має 8 граней (трикутники). У кожній вершині сходяться 4 ребра. Сума плоских кутів при кожній вершині дорівнює 4ˣ60=240. Має 8 граней, 6 вершин, і 12 ребер.

Октаедр символізує ПОВІТРЯ - «найповітряніший».

ФАКТ 5. Ікосаедр, від грецького «eikosi» - двадцять і «hedra» - грань. Має 20 граней (трикутних). У кожній вершині сходиться 5 ребер. Сума плоских кутів при кожній вершині дорівнює 5ˣ60=300. Має 20 граней, 12 вершин і 30 ребер.

Ікосаедр символізує ВОДУ, бо він «обтічний».

ФАКТ 6. Додекаедр, від грецького «dodeka» - дванадцять і «hedra» - грань. Має 12 граней (п'ятикутники). У кожній вершині сходяться 3 ребра. Сума плоских кутів при кожній вершині дорівнює 3ˣ108=360. Має 12 граней, 20 вершин і 30 ребер. Додекаедр втілює в собі все суще, символізує все СВІТОТВОРЕННЯ, вважався головним. 

V. ЦІНУВАННЯ. ОЦІНЮВАННЯ

Етап зорієнтований на логічне завершення уроку, підбиття підсумків щодо досягнення мети.

Мета – дати загальну оцінку рівню засвоєння знань та скоригованих/сформованих навичок під час уроку.

Вправи: підсумкове тестування.

Форми: індивідуальна.

Засоби: підсумковий тест, смартфони учнів.

5.1. Підсумковий тест

Методичний _{коментар}. Використовується підсумковий тест (таблиця 4, додаток Б), створений за допомогою сервісу Learningapps. Мета тестування – з’ясувати рівень знань учнів. За тест оцінка не виставляється, але (на розсуд викладача) може врахуватися в загальну оцінку роботи на уроці.

Рівні оцінювання тесту:

-         відмінний результат - 11-10 б.;

-         чудовий результат - 9-8 б.;

-         добрий результат - 7-6 б.;

-         треба повторити - менше 6 б.

           

Таблиця 4 - Підсумковий тест

Завдання	Посилання	QR-код
Учні/учениці на смартфонах виконують тест, який складається із 11 запитань з однією правильною відповіддю. Після закінчення вправи, викладач виводить тест на екран і разом з учнями обговорює запитання.	https://learni ngapps.org/ watch?v=p3 et3x72v23

5.2. Аналіз діяльності учнів на уроці

Методичний коментар. Викладач повинен об’єктивно оцінити роботу на уроці, акцентуючи увагу на позитивних прикладах.

VІ. ПОВІДОМЛЕННЯ ДОМАШНЬОГО ЗАВДАННЯ, РОЗ’ЯСНЕННЯ ЕТАПІВ ЙОГО ВИКОНАННЯ

Методичний _{коментар}. Домашнє завдання - заключна частина уроку. Воно повинно бути диференційованим, тобто доступним кожному учню. Диференційованість завдання дає можливість кожному виконати якусь його частину та отримати позитивну оцінку за роботу. Завдання розміщується на корпоративній платформі Google Classroom.

1.     Записати в зошит всі задачі, що було розглянуто на уроці 

Методичний коментар. Задачник викладено в Гугл Клас (додаток Г).

2.     Переглянути відеоколекцію «Многогранники»:

-          11 клас. Геометрія. Многогранник та його елементи. Опуклі многогранники: https://youtu.be/Bew5dav-Ny4?si=1h_Ai9HzL_fvooJE

-          Многогранники.         Розв'язування       завдань       ЗНО: https://youtu.be/R6tyU6Rw1UA?si=kquQvxsJGTNv8d2k

-          Урок №2. Многогранник та його елементи (11 клас. Геометрія): https://youtu.be/N6TqbOtuGX0?si=vsK6gyoq0DMHwlEJ

-          Урок №10. Правильні многогранники (11 клас. Геометрія):

https://youtu.be/6dNDI42uqE0?si=U_9rORGHzu6YH49C.

3.     Розв’язати задачу.

Площа підстави піраміди Хеопса являє собою квадрат 230 х 230 м. Знайти висоту піраміди Хеопса та площу її повної поверхні, якщо відомо, що бічні грані піраміди нахилені до площини основи під кутом, тангенс якого дорівнює 1,3.

Методичний _{коментар}. Розв’язок задачі представлено у додатку В.

4.     Виконати творче завдання (за бажанням):

-          розробити інфографіку з теми: «Тіла обертання»

-          підготувати творчу роботу «Многогранники у моїй професії».

        

Додаток А - Розірвані речення

Вкажіть два об'єкти, які відповідають одне одному.

Пара 1. Многогранник, який складається з плоского многокутника, точки, яка не лежить у площині плоского многокутника і всіх відрізків, що сполучають цю точку з точками плоского многокутника називається…пірамідою.

Пара 2. Точка, яка не лежить у площині основи піраміди називається…вершиною піраміди.

Пара 3. Відрізки, що сполучають вершину піраміди з вершинами основи, називаються…бічними ребрами.

Пара 4. Кожна бічна грань піраміди є…трикутником.

Пара 5. Перпендикуляр, опущений з вершини піраміди на площину основи називається…висотою піраміди.

Пара 6. Піраміда називається правильною, якщо її основа є…правильний многокутник, а основа висоти збігається з центром цього многокутника.

Пара 7. У правильній піраміді бічні грані …рівнобедрені трикутники.

Пара 8. Висота бічної грані правильної піраміди, проведена з її вершини, називається…апофемою.

Зайві елементи: площею, кубом, гіпотенузою.

           

Додаток Б–Підсумковий тест

1.                   Скільки існує правильних многогранників?

                             а) 8               б) 10           в) 5             г) безліч

2.                   У призми, що має 6 вершин, в основі лежить …

                             а) чотирикутник     б) шестикутник в) трикутник         г) п'ятикутник

3.                   Якого з правильних многогранників не існує?

                             а) додекаедр           б) гексаедр          в) пентаедр         г) октаедр

4.                   Бічними гранями похилого паралелепіпеда є …

                             а) квадрат     б) паралелограм           в) прямокутник г) трапеція

5.                   В основі піраміди SABCDEF лежить …

                     а) шестикутник б) п'ятикутник в) трикутник         г) чотирикутник

6.                   Оберіть формулу для обчислення площі повної поверхні призми.

                             а) Sпов=Sбіч+Sосн         б) Sбіч=PоснH           в) Sпов=Sбіч г) Sпов=Sбіч+2Sосн

7.                   Оберіть формулу для обчислення площі бічної поверхні правильної піраміди.

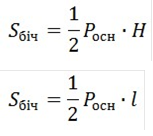
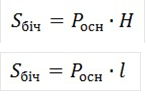в)  

а)  

г)

б)

8.                   Кількість яких елементів куба дорівнює шести?

                             а) вершин               б) ребер               в) діагоналей       г) граней

9.                   Многогранник, який складається з плоского многокутника, точки та відрізків, які їх з’єднують – це …

                             а) піраміда            б) конус               в) призма             г) циліндр

10.              Оберіть властивість правильної чотирикутної піраміди

                     а) бічні грані - трикутники                        в) усього граней 5

б) в основі лежить правильний      г) в основі лежить квадрат трикутник

11.              Знайдіть площу повної поверхні куба, ребро якогодорівнює5 см.

                                                   а) 150 см²                     б) 50 см²                 в)100 см²                г) 30 см²

Додаток В – Розв’язок задачі (домашнє завдання) Дано:

SABCD- піраміда ABCD – квадрат а= 230 м tg β =1,

Знайти: висоту піраміди

Розв’язок:

Кут нахилу бічної грані до площини основи – це кут між двома перпендикулярами, опущеними на спільне ребро.

Розглянемо _ SOМ. За означенням тангенса знайдемо висоту.

1)     SМ ⊥ СD, ОМ⊥ СD, (О - точка перетину діагоналей)

2)     SOМ: SO/ОМ = tg 1,3 

ОМ = ½×а = ½×230 = 115 (м)

SO = 115×1,3 = 149,5 (м)

3)     S_{пов. пов} = S_ос + S_біч, так як основа піраміди є квадрат ABCD, то S_осн = а²,  S_осн = 230² = 52900 (м²)

4)     Sбіч = SАSD + SDSC + SCSB+ SBSA = 4·Sтр, Sтр = ½ Р осн.×L 

Із ΔSOМ: ∠О = 90°, ОМ = 115м, SO = 149,5 м за теоремою Піфагора маємо, що SМ ² = ОМ² + SO² =149,5 ² + 115² = 22350,25 + 13225 = 35575,25;

SМ ≈ 189 м

S_біч = 1/2×(4×230)×SМ = 1/2×920×189 = 173880/2 = 86940 (м² )

S_{пов. пов} = S_ос + S_біч = 52900 + 86940 = 139840 (м²)

Відповідь: висота піраміди 149,5 м, площа 139840 м ².

           

Додаток Г – Задачник ЗАВДАННЯ №1. Варіанти відповіді:

А	Б	В	Г	Д

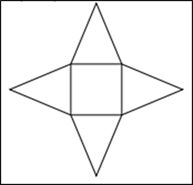Розгортку    якого з наведених          многогранників зображено на рисунку?

ЗАВДАННЯ №2.

Варіанти відповіді:

А	Б	В	Г	Д
7	8	9	16	17

піраміди.
ЗАВДАННЯ №3.		Варіанти відповіді:

Визначте     кількість граней   восьмикутної

А	Б	В	Г	Д
4	6	7	12	13

Скільки     всього         граней         у піраміди, яка має 12 ребер?

 

                         ЗАВДАННЯ №4.                Варіанти відповіді:

А	Б	В	Г	Д

Розгортку якого з наведених многогранників ЗАВДАННЯ №5.     Варіанти відповіді:

А	Б	В	Г	Д
6 см	8 см	9 см	12 см	18 см

Визначте довжину одного  ребра цього куба.
ЗАВДАННЯ №6.	Варіанти відповіді:

Сума довжин усіх ребер куба дорівнює    72      см.

А Б В Г Д 16   см2 32 см2 24 см2 64 см2 24 см2

                На    рисунку

зображено 

прямокутник         і  

трикутник, що є гранями правильної

трикутної призми. Периметр цього прямокутника дорівнює 38 см. Визначте площу основи цієї призми, якщо довжина висоти           призми        дорівнює 11 см.
ЗАВДАННЯ №7.	Варіанти відповіді:

А	Б	В	Г	Д
0o	30o	45o	60o	90o

На рисунку зображено куб      ABCDA₁B₁C₁D₁.

Визначте градусну міру кута  між прямими АВ₁ і DD₁.

 

А	Б	В	Г	Д
100√3	100	400√3		200

ЗАВДАННЯ №8.    Варіанти відповіді: На   рисунку      зображено розгортку піраміди,    що складається    з        квадрата,     

сторона якого дорівнює 10 см, і         чотирьох     правильних трикутників. Визначте площу бічної поверхні цієї піраміди.

 

ЗАВДАННЯ №9.

Обчисліть площу бічної поверхні правильної чотирикутної призми, діагональ якої дорівнює 12 см і нахилена до площини основи під кутом 30°.

ЦІКАВІ ФАКТИ

ФАКТ 1. Усі правильні многогранники були відомі в Стародавній Греції. Їм присвячена заключна 13-а книга знаменитих «Начал». Усього існує п'ять унікальних форм. Їх називають Платоновими тілами. Правильні многогранники по- грецьки закінчуються на едр (edrа-грань).

ФАКТ 2. Тетраедр - від «тетра» – чотири і грецького «hedra» – грань. Складається з 4-х правильних трикутників, в кожній його вершині сходяться 3 ребра. Сума плоских кутів при кожній вершині дорівнює 3ˣ60=180. Має 4 грані, 4 вершини і 6 ребер. Тетраедр символізував ВОГОНЬ, бо його вершина спрямована вгору.

ФАКТ 3. Гексаедр, від грецького «гекса» – шість і «hedra» - грань. Має шість квадратних граней, у кожній його вершині сходяться 3 ребра. Сума плоских кутів при кожній вершині дорівнює 3ˣ90=270. Має 6 граней, 8 вершин і 12 ребер. Гексаедр більш відомий як куб. Гексаедр - ЗЕМЛЯ, бо він «найстійкіший».

ФАКТ 4. Октаедр, від грецького «okto» - вісім і «hedra» - грань. Має 8 граней (трикутники). У кожній вершині сходяться 4 ребра. Сума плоских кутів при кожній вершині дорівнює 4ˣ60=240. Має 8 граней, 6 вершин, і 12 ребер. Октаедр символізує ПОВІТРЯ - «найповітряніший».

ФАКТ 5. Ікосаедр, від грецького «eikosi» - двадцять і «hedra» - грань. Має 20 граней (трикутних). У кожній вершині сходиться 5 ребер. Сума плоских кутів при кожній вершині дорівнює 5ˣ60=300. Має 20 граней, 12 вершин і 30 ребер.

Ікосаедр символізує ВОДУ, бо він «обтічний».

ФАКТ 6. Додекаедр, від грецького «dodeka» - дванадцять і «hedra» - грань. Має 12 граней (п'ятикутники). У кожній вершині сходяться 3 ребра. Сума плоских кутів при кожній вершині дорівнює 3ˣ108=360. Має 12 граней, 20 вершин і 30 ребер. Додекаедр втілює в собі все суще, символізує все СВІТОТВОРЕННЯ, вважався головним.