План - конспект уроку з теми "Числові нерівності"

План – конспекту уроку

Тип уроку: ознайомлення з новим матеріалом.

Тема: « Числові нерівності. Основні властивості числових нерівностей»

Мета:

         навчальна: формування знань про числові нерівності, їх основні властивості;

          розвивальна:  розвивати уміння порівнювати , здатність самостійно розв’язувати  задачі, підводити підсумки;

          виховна: виховувати відповідальне відношення до навчання.

Структура уроку

1.Організаційний момент (2 хв.)

2.Підготовка до вивчення нового матеріалу повторенням вивченого ( 3 хв.)

3.Ознайомлення з новим матеріалом( 25хв.)

4.Застосування вивченого до розв’язку прикладів ( 10 хв.)

5.Постановка домашнього завдання (2 хв.)

6.Підведення висновків уроку перевіркою знань (фронтальне опитування;  3 хв.)

7.Резервні приклади.

Хід уроку

1. Організаційний момент.

Перевірити підготовленість класного приміщення та готовність учнів до уроку.

2. Підготовка до вивчення нового матеріалу повторенням вивченого.

Згадати з учнями додатні та від’ємні числа; координатну пряму, на якій точками зображуються дійсні числа; що означають знаки  <  і  >.

Увагу учнів треба акцентувати на вміння порівнювати числа. Тому можна запропонувати наступні приклади:

1. Який запис правильний: а) 3 < 5; б) 6 > 8; в) 0 < 1 ?
2. Розмістіть у порядку зростання числа: 2, 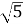, -12, 2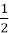, 0, -3π.
3. Яке з чисел 1, 5, 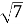, , 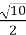-42,3 найбільше?

3.Ознайомлення з новим матеріалом.

Означення: Два вирази, з’єднані між собою одним із знаків >, <,  ≥ , ≤ -  утворюють нерівність.

Приклади нерівностей: 3 , 3х – 5 ≥ 0.

Число а вважається більшим від b, якщо різниця a – b – число додатне; число а менше від b, якщо  a – b – число від’ємне.

Якщо обидві частини нерівності – числа, її називають числовою нерівністю. Такі нерівності бувають правильні й неправильні. Наприклад, з нерівностей  2 < 3, , -3 < -5 дві перші правильні, а третя – неправильна, бо число -3 більше від -5.

Властивості числових нерівностей

Теорема 1. Якщо a < b  і b < c, то a < c.

Доведення. Якщо a < b  і b < c, то числа  a – b і b – с – від’ємні. Їх сума (a – b) + (b – с ) = a – с – число також від’ємне. А якщо  a – с - число від’ємне, то a < c. Це й треба було довести.

Приклад. Оскільки і 1,42, то 1,42.

Теорема 2. Якщо до обох частин правильної нерівності додати одне й те саме число, то отримаємо правильну нерівність.

Доведення. Якщо a < b, то  a – b - число від’ємне. Оскільки  a – b=( a + с) – (b + с) - число також від’ємне. А це означає, що  a + с < b + с.

Наприклад, якщо a < b  і  c – довільне дійсне число, то a + с < b + с.

Теорема 3. Якщо обидві частини правильної нерівності помножити на одне й те саме додатне число, то отримаємо правильну нерівність. Якщо обидві частини правильної нерівності помножити на одне й те саме від’ємне число і змінити знак нерівності на  протилежний, то отримаємо правильну нерівність.

Доведення. Нехай  a < b  і  c – будь-яке додатне число. У цьому випадку числа  a – b, (a – b) c, а отже, і різниця ас – bс – від’ємні, тобто ас < bс .

Якщо a < b  і  c – будь-яке від’ємне число, то добуток  (a – b) c, а отже, і різниця ас – bс – числа додатні. Тому ас > bс .

Теорема 4. Нерівності з однаковими знаками можна почленно додавати.

Доведення. Якщо  a < b і c < d , то за теоремою 2  a + c < b + c і b + c < b + d, звідси  a + c < b + d.

Теорема 5. Нерівності з однаковими знаками можна почленно перемножати, якщо їх ліві і праві частини – додатні числа.

Доведення. Нехай  a < b і c < d, а числа c і d – додатні. Згідно з теоремою 3 ас < bс і bс < bd, звідки за теоремою 1 ас < bd.

4.Застосування вивченого до розв’язку прикладів.

Учні біля дошки розв’язують наступні приклади ( Г. П. Бевз Алгебра 9 клас):

20Покажіть, як розміщені на координатній прямій точки з координатами a, b, c і d, якщо  a < c, b> c, d > b.

21Запишіть правильну нерівність, утворену в результаті:

а) додавання до обох частин нерівності 12 < 18 числа 5;

б) віднімання від обох частин нерівності 12 < 18 числа 77;

в) множення обох частин нерівності 12 < 18 на 3; на -5;

г) ділення обох частин нерівності 12 < 18 на 3; на -6.

23Відомо, що а > b. Поставте замість * знак нерівності:

1. 2a * 2b;
2. 1,5a * 1,5b;
3.  –a * - b;

4. -3a * -3b.

25Додайте почленно нерівності:

а) 5 < 12 і 7 < 8;    б) 3 < 6  і  -3 < -2;

в) 5 < 6 і x < z;       г) a <  b і  x ≤  z.

5.Постановка домашнього завдання.

Прочитати  §2 підручника, вивчити теореми 1- 5; розв’язати :

26.Перемножте почленно нерівності:

а) 2 < 3  і  5 < 8;    б) 5 < 7  і  ;

в) і ;     в) -4 < -1 і -5 < -4.

27.Доведіть, що коли a < b і ab < 0, то   .

31.Доведіть, що коли:

а) a ≤ b і b ≤ c, то  a ≤ c;

б) a ≤ b і c > 0, то  ac ≤ bc;

в) a ≤ b і c < 0, то  ac ≥ bc.

6.Підведення висновків уроку перевіркою знань.

В ході фронтального опитування разом з учнями підвести підсумки уроку. Запропонувати наступні питання:

• Сформулюйте означення нерівності
• Яка нерівність називається правильною
• Які властивості нерівностей ви знаєте

7. Резервні приклади.

У випадку дострокового виконання класом запропонованих вище прикладів, можна запропонувати наступні приклади:

32.Чи правильно, що при додатних значеннях a і b:

a) з a < b випливає ;

b) з   випливає a < b;

c) з a < b випливає ;

d) з     випливає a < b?

33.Доведіть, що а) діагональ чотирикутника менша від його півпериметра; б) сума діагоналей чотирикутника менша від його периметра.