План – конспект "Функція. Область визначення та область значень функції"

Розгорнутий план – конспект уроку алгебри

Урок № 44

Клас: 6

Тип уроку: засвоєння нових знань

Тема: Функція. Область визначення та область значень функції

Мета:

•   навчальна: домогтися усвідомлення учнями змісту понять «функція», «функціональна залежність», «область визначення функції», «область значень функції», способи задання функції; здійснити первинне закріплення змісту вивчених понять; розпочати роботу з вироблення вмінь: а) задавати функціональні залежності формулами; б) працювати із функціями, заданими таблицею; в) обчислювати за формулою значення функції, якщо відомо значення аргументу, та розв'язувати обернену задачу.
•   розвиваюча: розвивати навички самоконтролю, логічне мислення, математичну мову, інтуїцію, вміння самостійно працювати та працювати в групах.
•   виховна: виховувати в учнів самостійність, кмітливість, старанність, наполегливість, творчу й пізнавальну самостійність.

 

План уроку

1.Організаційний етап (2 хв.)

2. Постановка цілі і мотивація(2 хв.)

3.Актуалізація опорних знань(5 хв.)

4. Вивчення нового матеріалу(20 хв.)

5. Закріплення нових знань(13хв.)

6. Підсумки уроку (3 хв.)

 

 

 

 

 

 

Хід уроку

1. Організаційний момент (вчитель перевіряє готовність учнів до уроку та відмічає відсутніх)

Девізом сьогоднішнього уроку будуть слова давньогрецького математика Фалеса: «Що найбільше на світі? Простір. Що найшвидше за все? Розум. Що мудріше за все? Час. Що найприємніше за все? Досягти бажаного».

Хочеться, щоб кожен з вас на сьогоднішньому уроці досяг бажаного результату. А саме: зрозумів дану тему.

Відкриваємо зошити і записуємо тему уроку: «Функція. Область визначення та область значень функції».

2. Постановка цілі і мотивація

Тема «Функція» є однією з найбільш важливих тем, які вивчають в шкільному курсі алгебри. Ми будемо розглядати її протягом 8 уроків, а по закінченню напишемо підсумкову контрольну роботу.

«Немає жодної галузі людського знання, куди не входили б поняття про функції та їх графічне зображення» – К. Ф. Лебединцев (видатний методист математик)

Впродовж занять, присвячених даній темі, ми повинні вивчити:

•   що таке функція?
•   Що таке область визначення і область значень функції?
•   Які існують способи задання функції.
•   Навчитись наводити приклади функцій.
•   Зрозуміти слова К. Ф. Лебединцева.

3.Актуалізація опорних знань

Для початку попрацюємо усно. Я буду зачитувати вам твердження, а ви повинні визначити, чи є воно істинним.

•   Вік людини залежить від його зросту.
•   Урожайність залежить від кількості корисних речовин у ґрунті.
•   Кількість поганих оцінок залежить від кількості похмурих днів у році.
•   Вартість квитка на автобус залежить від  кількості кілометрів, які вам потрібно проїхати.

Скажіть, будь ласка, на якому слові акцентується увага в кожному з даних тверджень? – Залежність.

Майже все, що відбувається з нами чи довкола нас, залежить одне від одного. На сьогоднішньому занятті ми з'ясуємо, як такі залежності ви­значаються в математиці та які математичні поняття з ними пов'язані.

 

4. Вивчення нового матеріалу

Приклад№1

а	3	5	6
Р

 

а – довжина сторони;

Р – периметр квадрата;

Р=4×а – формула для знаходження периметра квадрата.

1. Скажіть, будь ласка, від чого залежить периметр квадрата? Значення периметра залежить від того, яких значень набуває довжина сторони квадрата.
2. Чи може у квадраті зі стороною а см. бути два різні периметри? Потрібно зауважити, що кожному значенню довжини сторони відповідає єдине значення периметра. У даному прикладі маємо залежність між двома змінними а і Р. Значення змінної а  вибираються довільно, а значення змінної Р залежать від вибраних значень а. Тому а називають незалежною змінною, а Р – залежною змінною.

Отже, ми з вами розглянули залежність між двома величинами та визначили, що кожному значенню незалежної змінної відповідає єдине значення залежної змінної.

Саме такі залежності називають функціями.

Записуємо в зошити: функція – це залежність між двома змінними, якщо кожному значенню незалежної змінної відповідає єдине значення залежної змінної.

Історична пауза

Слово «функція» (з лат. мови – виконання, дія) було вперше вжито німецьким математиком Лейбніцом в 1673 році (під функцією він розумів відрізок, довжина якого змінювалась згідно певного закону). Зусиллями багатьох математиків поняття функції уточнювалось, розширювалось і наповнювалось новим змістом.

Найзагальніше сучасне означення функції запропонували в ХХ ст. група математиків, яка виступала під псевдонімом Бурбакі: «функція – це відношення, при якому кожному елементу області відправлення відповідає рівно один елемент області прибуття».

 

В математиці незалежну змінну позначають х і називають «аргументом». Залежну змінну позначають у і називають «функцією від змінної х».

Термін «функція» використовується у двох значеннях – як сама залежність та як значення залежної змінної.

Область визначення функції – D(y) – усі значення, яких набуває незалежна змінна х.

Область значень функції – E(y) – усі значення, яких набуває залежна змінна у.

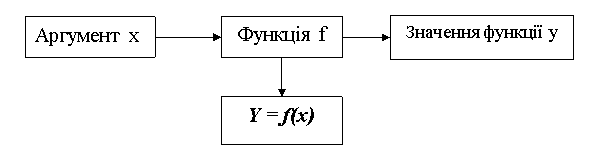
Задати функцію f означає встановити закон, за яким значення y обчислюється за даним значенням x. Розрізняють основні методи задання функціональної залежності між величинами:

•   за допомогою таблиці (табличний) – для певних значень аргументу вже внесені відповідні значення функції, які не потрібно обчислювати. Основним недоліком табличного методу є його громіздкість.
•   За допомогою формули (аналітичний) – дає можливість знаходити значення функції для будь-якого значення аргументу; найзручніший спосіб, займає всього один рядок; якщо немає ніяких обмежень для змінної х, то областю визначення функції є всі значення х, при яких формула має зміст.
•   Словесний метод.
•   За допомогою графіка (графічний) – на координатній площині відкладаються точки, координатами яких будуть відповідно пари (х; у).

Приклад №1

Нехай функцію задано формулою f(x)= 2х+1 (словесний опис: значення функції дорівнює подвоєному аргументу, збільшеному на одиницю).

 

Завдання 1: знайдіть область визначення D(y), область значень функції E(y); знайдіть значення функції, якщо х=2, -2, 0.

Розв’язання:

f(2)=5; f(-2)=-3; f(0)=1.

Завдання 2: знайдіть значення аргументу, якщо у=11, 7, -19.

Розв’язання:

2х+1=11 2х=10 х=5

2х+1=7 2х=6   х=3

2х+1=-19  2х=-20  х=-10

5. Закріплення нових знань

 

№715

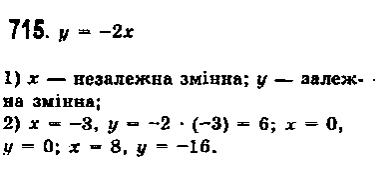
№716

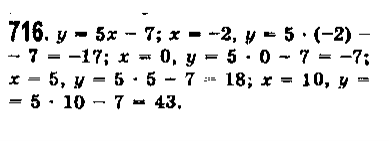
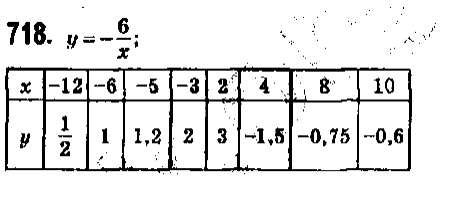
№718

 

 

 

 

 

 

 

№720

 

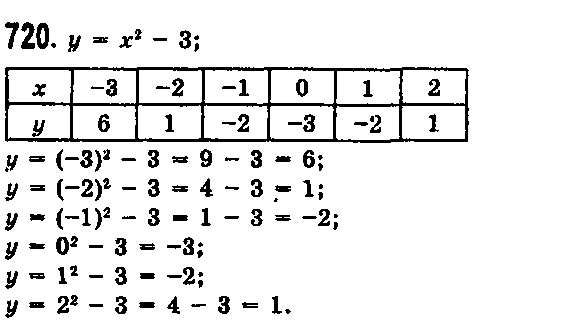
6. Підсумки уроку. Рефлексія. Домашнє завдання.

Саме час повернутись до нашого девізу і зрозуміти, чи ми з вами досягли нашої мети? Чи зрозуміли ви, що таке функція?

 

Домашнє завдання: §19 вивчити означення функції, області визначення та області значень функції. Підібрати приклад функції з будь-якої галузі науки.

№714

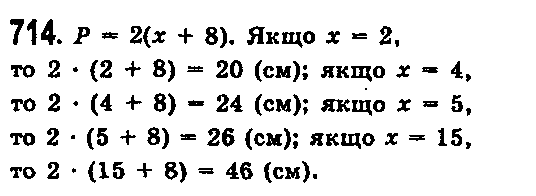
№717

 

 

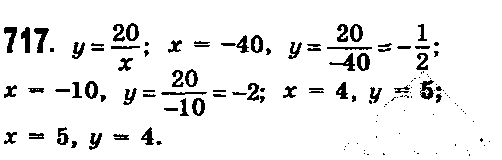
№719

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

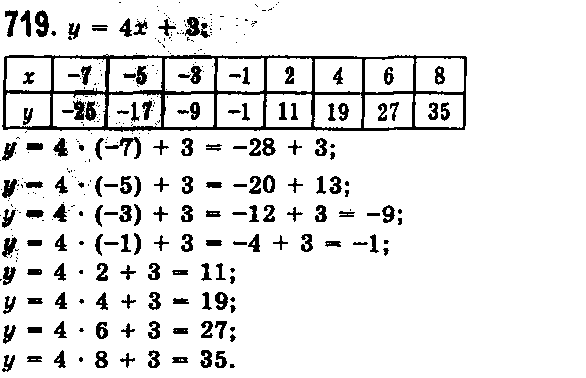
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

 

1. Істер О.С. Алгебра: підруч. для 7-го кл. загальноосвіт. навч. закл. / О.С. Істер. – Київ: Генеза, 2015. -256 с.