План-конспект уроку: "Подібність трикутників. Ознаки подібності трикутників"

Тема уроку: Подібні трикутники. Ознаки подібності трикутників

Мета уроку:

• навчальна - сформувати в учнів уявлення про подібні трикутники; працювати над засвоєнням учнями означення подібних трикутників, змісту поняття коефіцієнта подібності; ознайомити учнів із ознаками подібності трикутників;
• розвивальна - розвивати логічне мислення і вміння аналізувати та узагальнювати;
• виховна - виховувати дисциплінованість та свідоме ставлення до вивчення геометрії, повагу до думки інших.

Тип уроку: засвоєння нових знань. 

Наочність та обладнання: презентація «Подібні трикутники», конспект «Подібні трикутники. Ознаки подібних трикутників», приладдя.

 

Хід уроку

 

І. Організаційний етап

Відомий філософ досократського періоду, математик, астроном Фалес  Мілетський одного разу зауважив: «Блаженство тіла полягає в здоров'ї, а блаженство розуму – у знанні». Ці слова ми візьмемо за епіграф нашого уроку.

 

Перед вивченням нової теми, я пропоную згадати деякі означення та властивості з курсу математики 6 класу.

 

ІІ. Актуалізація опорних знань

 

Фронтальне опитування:

• Що називається відношенням двох чисел?(частка двох чисел)

• Чи вірні рівності: 3/5 = 6/25; ні 3/5 = 0,6;так  0,8 / 3 = 8/3;ні 15/10 = 25/20?ні

• Кожне із записаних рівностей є рівність двох відношень. Як називається ця рівність?(пропорція)

• У пропорції вкажіть крайні і середні члени: 8/3 = 5/30; 12 / 0,2 = 30 / 0,5.

• Сформулюйте основну властивість пропорції. (добуток крайніх членів пропорції дорівнює добутку її середніх членів.)

• Чи вірні пропорції 8/3 = 5/30; 12 / 0,2 = 30 / 0,5? (Ні;так)

 

 

ІІI. Мотивація навчальної діяльності

     З пропорціями мали справу стародавні будівельники, Правильні співвідношення, за допомогою яких будувалися  палаци і храми надавали цим будівлям ту незвичайну красу, яка захоплює нас і сьогодні. За допомогою пропорцій в Вавилоні малювали плани міст. Після того, як під час розкопок звірили ці плани з самими розкопками, з'ясували, що плани виконані з великою точністю. Давньогрецькі математики дуже майстерно перетворювали пропорції, доводили з їх допомогою найскладніші затвердження, вирішували найскладніші завдання.

       У геометрії теж існує поняття відношення і пропорційності. У повсякденному житті зустрічаються предмети однакової форми, але різних розмірів, наприклад, футбольний м’яч та металева кулька, картина та її фотознімок, літак і його модель. Якщо довжина моделі літака в 100 разів менша від довжини справжнього літака, то і довжина крила моделі має бути в 100 разів меншою від довжини крила справжнього літака.   У геометрії фігури однакової форми прийнято називати подібними. Якщо дві фігури подібні, то їх відповідні розміри пропорційні.

 

Тема нашого уроку: «Подібні трикутники. Ознаки подібності трикутників»

Отже, введемо поняття подібних трикутників.

 

IV. Засвоєння знань

План вивчення нового матеріалу

1. Уявлення про подібні фігури.
2. Означення подібних трикутників.
3. Властивості відповідних елементів подібних трикутників.
4. Перша ознака подібних трикутників.

 

 

Означення. Два трикутники називаються подібними, якщо кути одного з них відповідно дорівнюють кутам іншого і відповідні сторони цих трикутників пропорційні:

або ::. 

Розглянемо 2 трикутники:

 

 

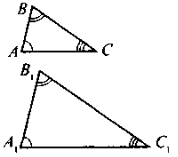
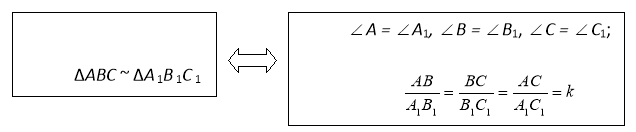
Число k—коефіцієнт подібності.

У геометрії подібність фігур використовується часто, тому існує і загальноприйнятий знак подібності ~

Задача 1. Відомо, що ΔАВС ~ ΔKMN. Назвіть відповідно рівні кути цих трикутників.

( )

 

Ознаки подібності трикутників

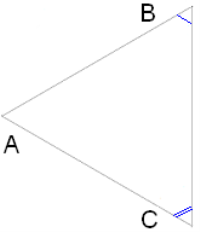
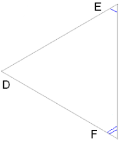
1. Якщо два кути одного трикутника відповідно дорівнюють двом кутам іншого, то такі трикутники подібні.

Якщо ∠B= ∠E і ∠C= ∠F, тоді ΔABC∼ΔDEF.

 

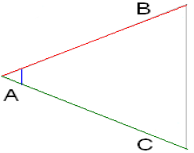
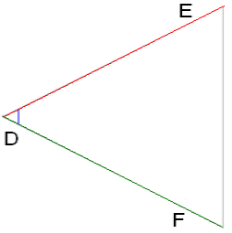
2. Якщо дві сторони одного трикутника пропорційні двом сторонам іншого трикутника і кути, утворені цими сторонами рівні, то такі трикутники подібні.

Якщо AB/DE=AC/DF і ∠A= ∠D, тоді ΔABC∼ΔDEF.

 

 

3. Якщо три сторони одного трикутника пропорційні трьом сторонам іншого, то такі трикутники подібні.

Якщо AB/DE=BC/EF=AC/DF, тоді ΔABC∼ΔDEF.

 

 

V. Формування первинних умінь

Виконання усних вправ (робота в парах)

 

«Спіймай помилку» ( діти читають завдання і відповідь на нього та знаходять помилки)

1. Трикутник АВС і трикутник з вершинами D, E, F подібні, причому 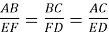. Закінчіть запис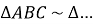

()

2. Чи можуть бути подібними прямокутний і тупокутний трикутники?

Так.

( Ні, бо в прямокутному і тупокутному трикутниках не можуть бути рівними всі кути)

3. Два трикутники подібні з коефіцієнтом 0,25. У скільки разів сторони одного трикутника більші за відповідні сторони іншого?

Сторони одного трикутника в 25 разів більші за сторони іншого.

( У 4 рази сторони одного трикутника більші за відповідні сторони іншого трикутника)

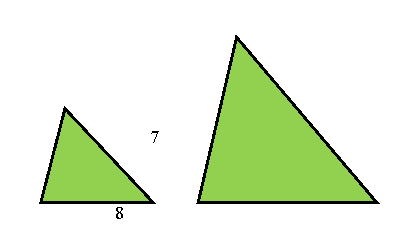
1. Задачі за готовими малюнками:

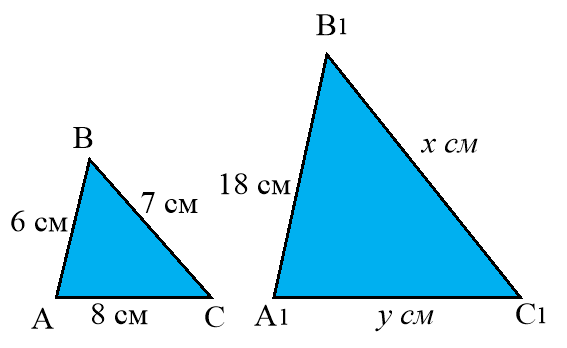
Дано: ~ 

Знайти: .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

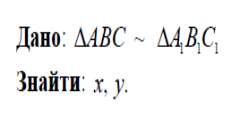
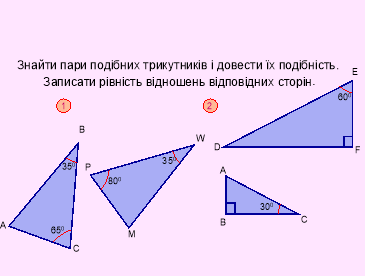
IV. Розв’язування задач.

1. Завдання  (робота класом).
2.   До речі, подібна задача була запропонована випускникам на ЗНО у 2009 році. (Рисунок)

 

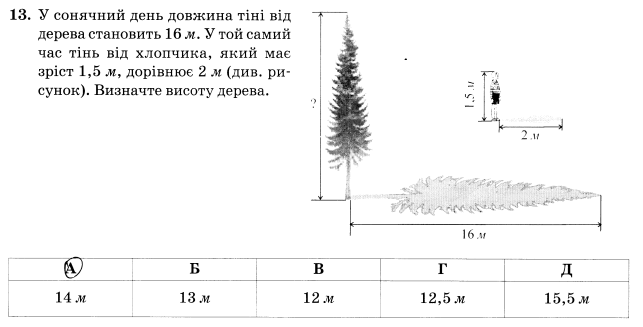
Задача. Які завбільшки повинні бути букви на класній дошці, щоб учні, сидячи за партами, бачили їх так само виразно, як букви в своїх книжках (на відстані 25см від ока)? Відстань від парт до дошки взяти 5м. Ширина букви в книжці дорівнює 1мм.

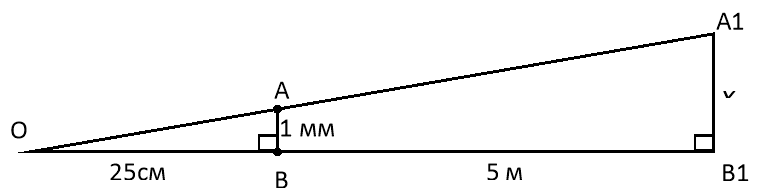Розв’язання                                                                                            

 

                         

 

Розглянемо і .спільний, так як - відстань до книжки від читача; - відстань від читача до дошки. , , то .  ~ (за основною теоремою подібності трикутників), звідси

 

 

В-дь: 2,1 см

2. Розв’язуємо задачі в групах.

Завдання для І, ІV груп. З допомогою фотографії виміряти висоту вежі.

Розв'язання.

Висота вежі відноситься до довжини основи так як висота трикутника на фото до основи трикутника. Нехай висота вежі, то

.

В-дь: 28 м.

 

 

 

Завдання для ІІ, V груп. З допомогою фотографії виміряти висоту вежі

 Розв'язання.

 

Висота вежі відноситься до довжини основи так як висота трикутника на фото до основи трикутника. Нехай висота вежі, то

.

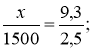
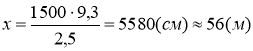В-дь: 56 м.

 

 

 

 

 

 

Також існує історичний факт, що Фалес вимірював висоту піраміди за допомогою жердини ,не в найпростішому випадку, коли довжина тіні вертикально поставленої віхи дорівнює довжині самої віхи, а в загальному, скориставшись методом встановлення пропорційного відношення між трьома величинами, які можна виміряти, і шуканою величиною – висотою піраміди.

 

 

VІ. Підведення підсумків уроку

Інтерактивна вправа «Результат»

Учні по черзі закінчують речення

• сьогодні я на уроці повторив….
• сьогодні я на уроці я навчився…
• мені необхідно попрацювати над….
• Найважчим для мене було…

Учитель виставляє оцінки і бажає: нехай удача та успіх завжди поруч ідуть.

 

 

VІI. Домашнє завдання

Опрацювати § 9,10.

Виконати № 414, 440*.