Презентація "Подібність трикутниів. Ознаки подібності трикутників"
Про матеріал
Відомий філософ досократського періоду, математик, астроном Фалес Мілетський одного разу зауважив: «Блаженство тіла полягає в здоров'ї, а блаженство розуму – у знанні». Ці слова ми візьмемо за епіграф нашого уроку. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


























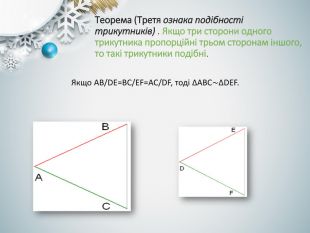


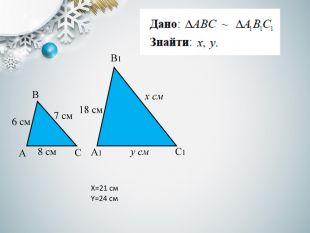
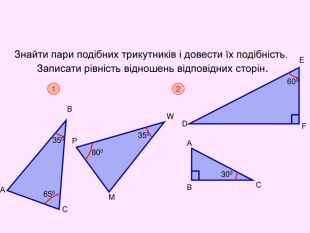








-

Данилець Вікторія
12.12.2024 в 10:42
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сеннікова Тетяна Сергіївна
08.11.2024 в 18:34
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гелешко Наталія
09.03.2024 в 16:54
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Неміш Олена Віталіївна
13.12.2022 в 15:30
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Poll Olena
03.02.2022 в 09:13
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Константинова Олена Павлівна
21.12.2021 в 23:47
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Voytenko Yulia
19.12.2021 в 23:35
Дякую
Загальна:
4.7
Структурованість
4.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Шама Олена
29.11.2021 в 20:47
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 5 відгуків