ОПОРНІ СХЕМИ "Центральні, вписані кути. Описані та вписані чотирикутники"+ усне розв"язування задач за готовими малюнками
Про матеріал
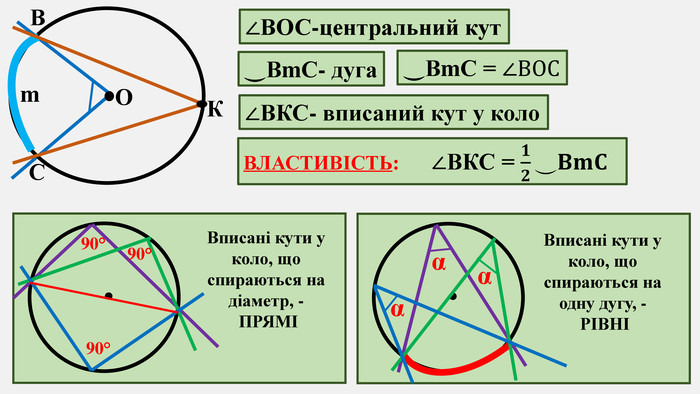
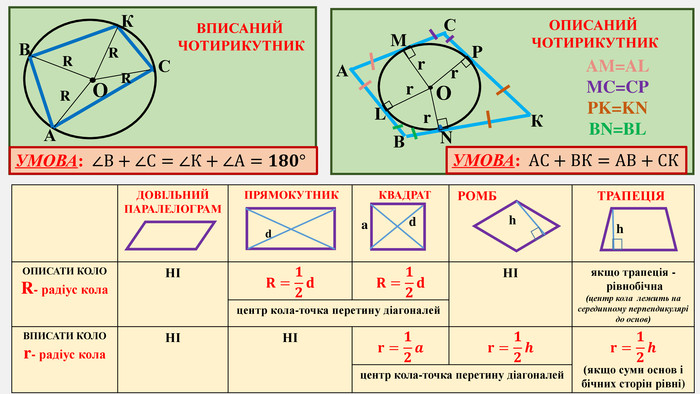
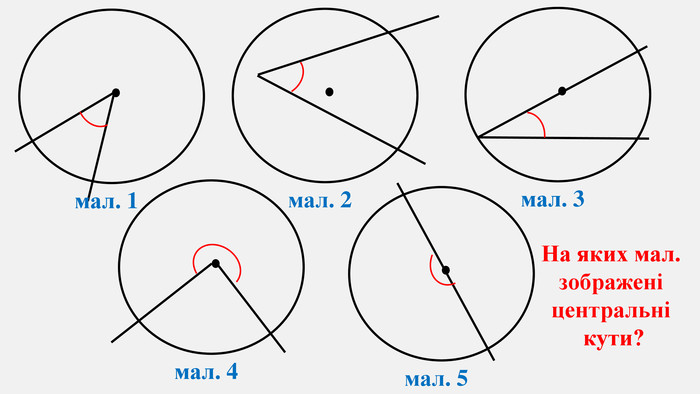
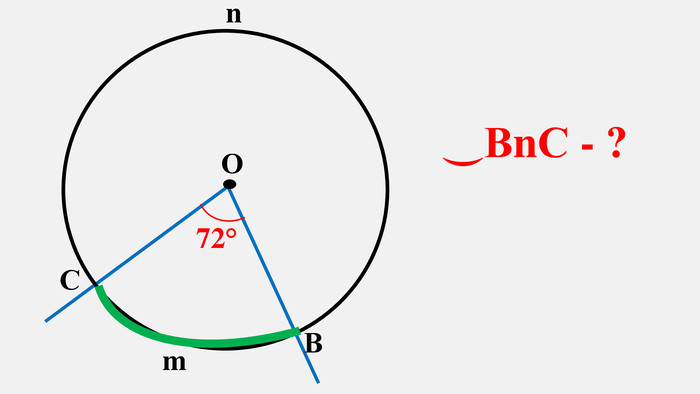
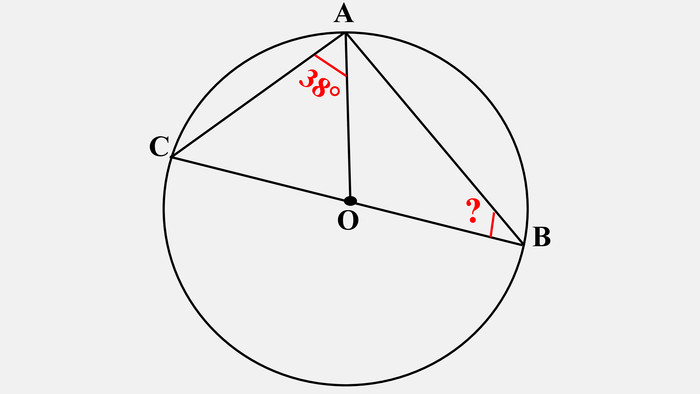
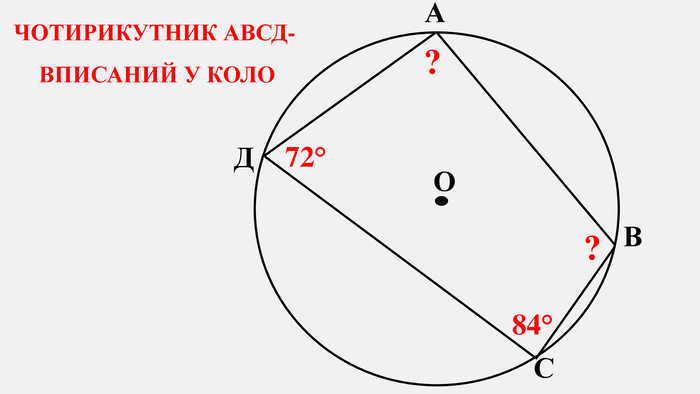
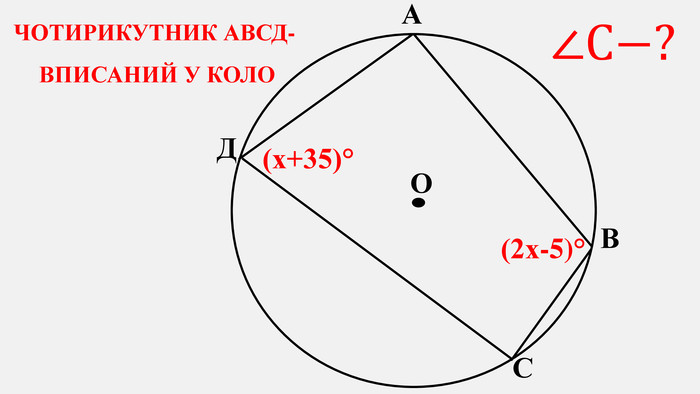
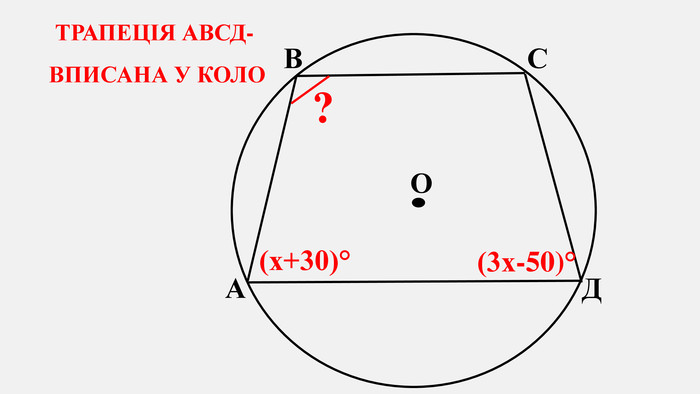
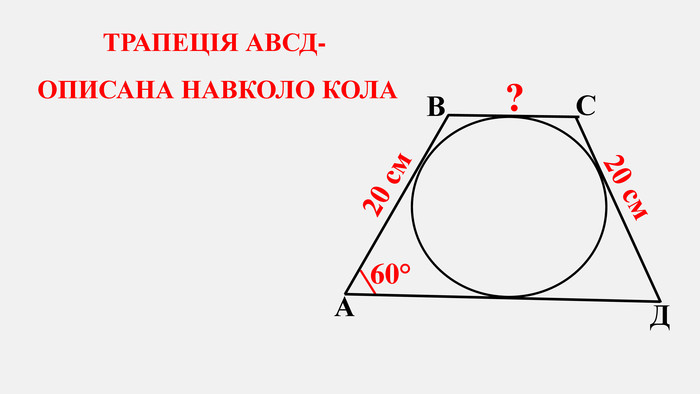
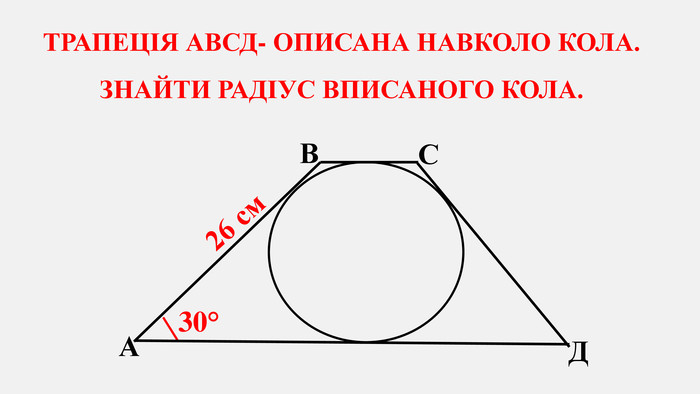
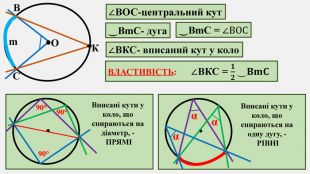
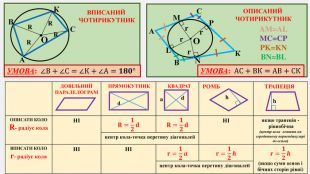
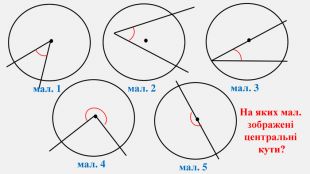
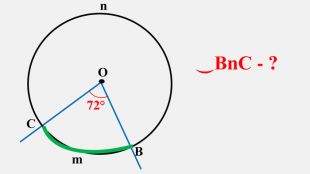
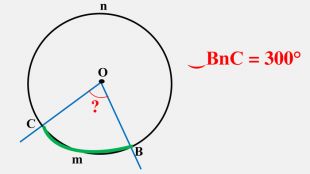
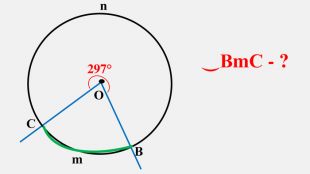
Узагальнено і систематизовано навчальний матеріал з теми "Центральні, вписані кути. Описані та вписані чотирикутники". Запропоновані задачі за готовими малюнками з даної теми. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку

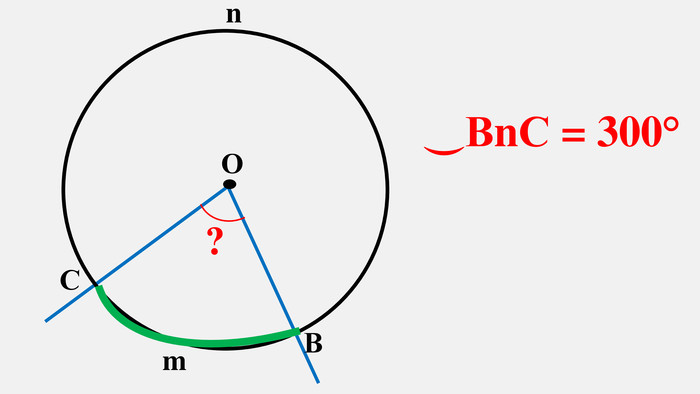
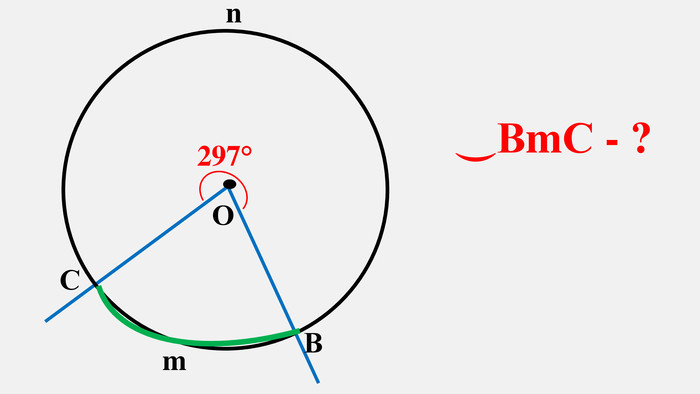

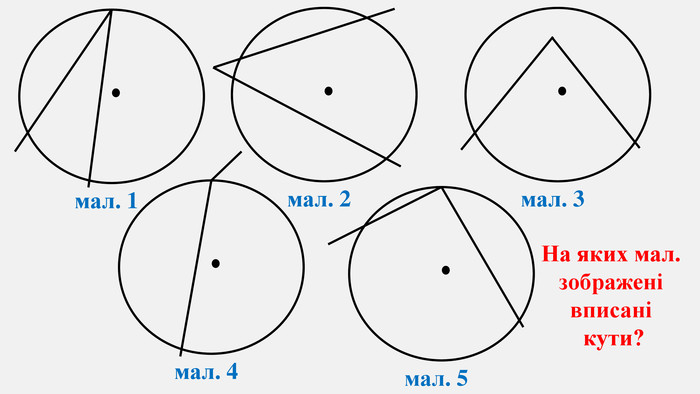
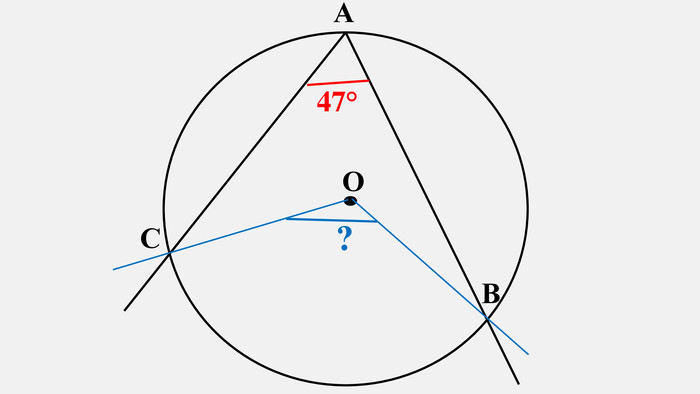
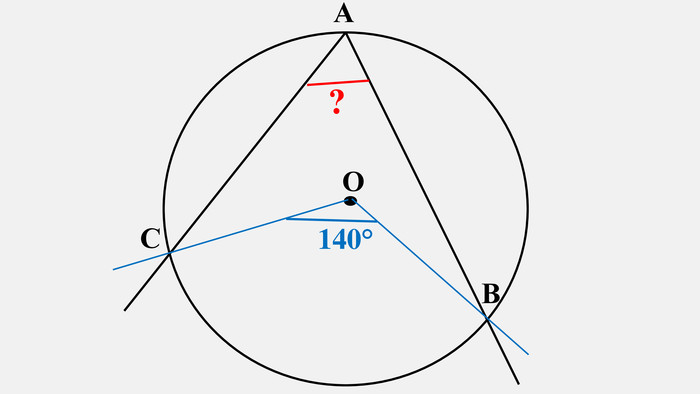
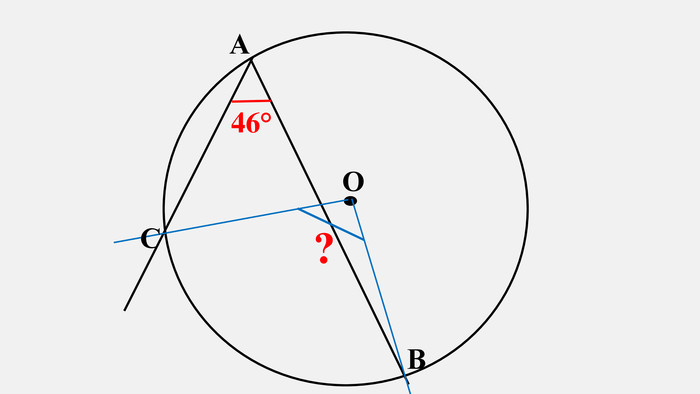
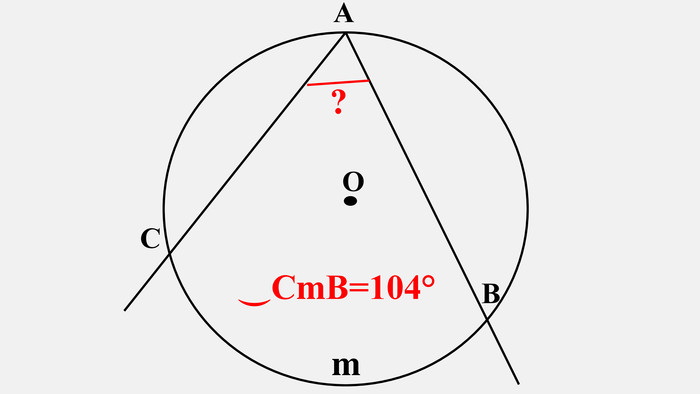
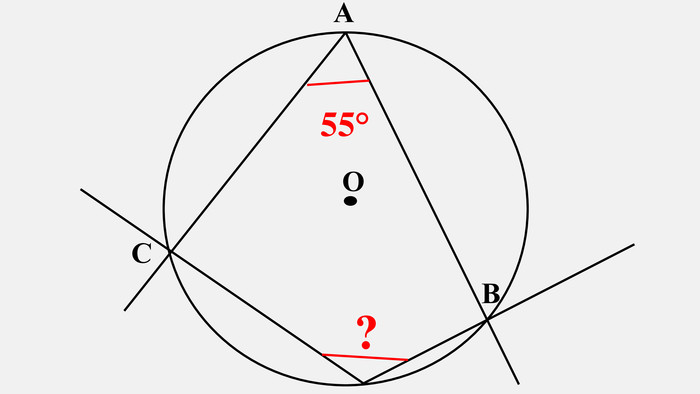

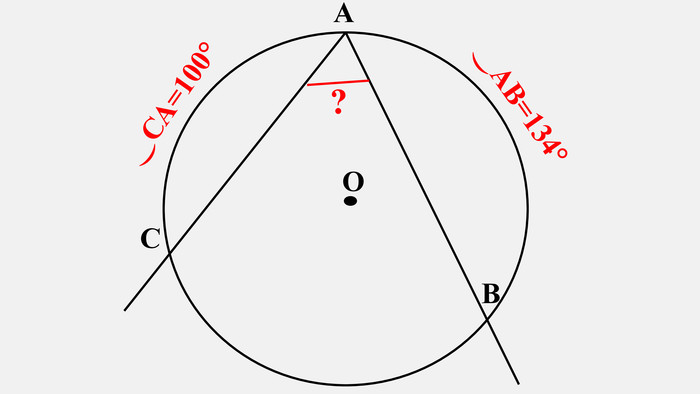
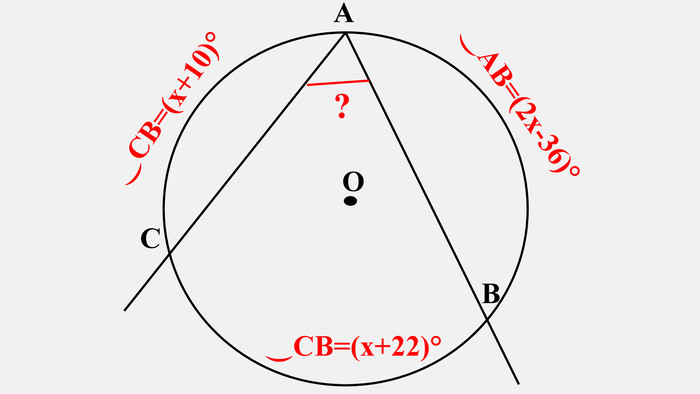
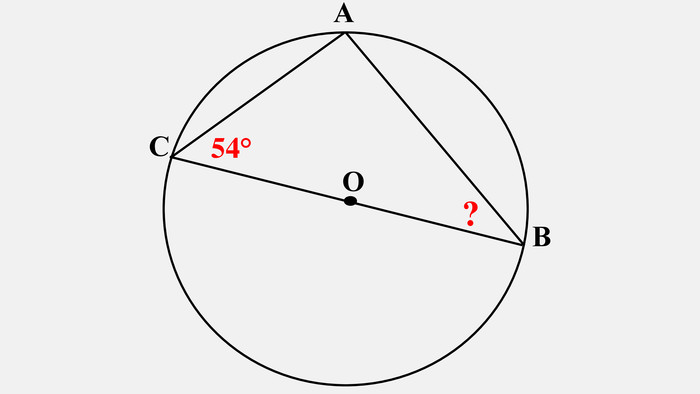

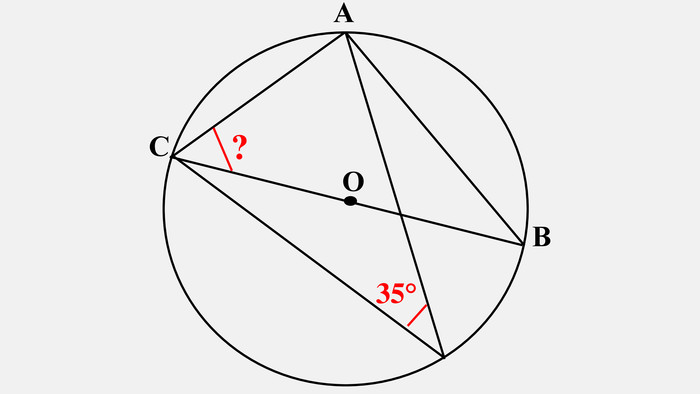
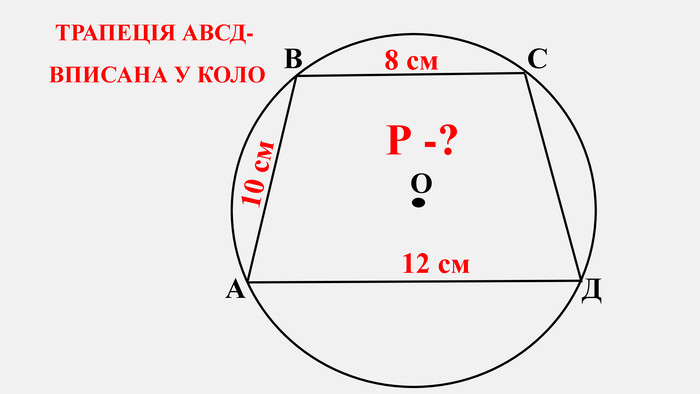
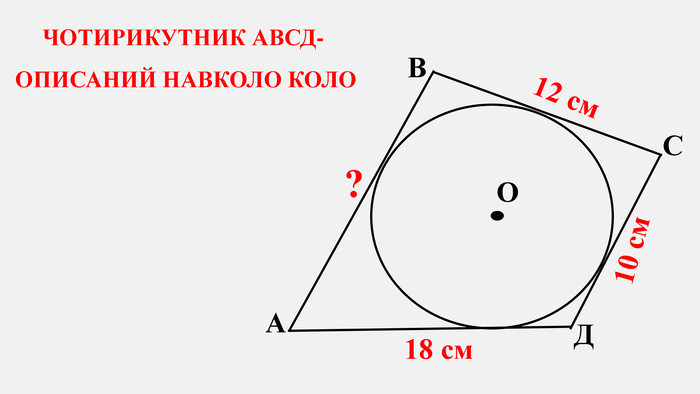
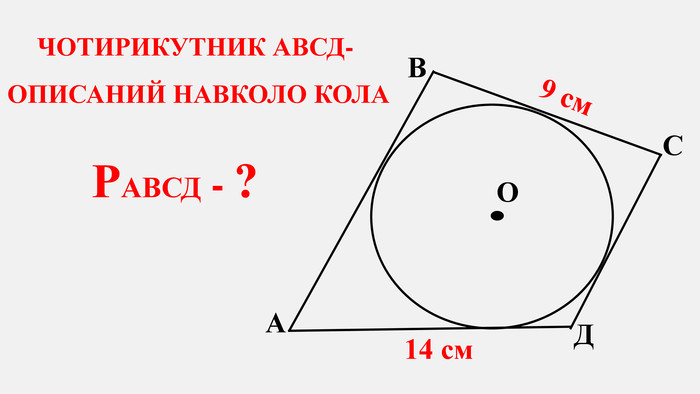
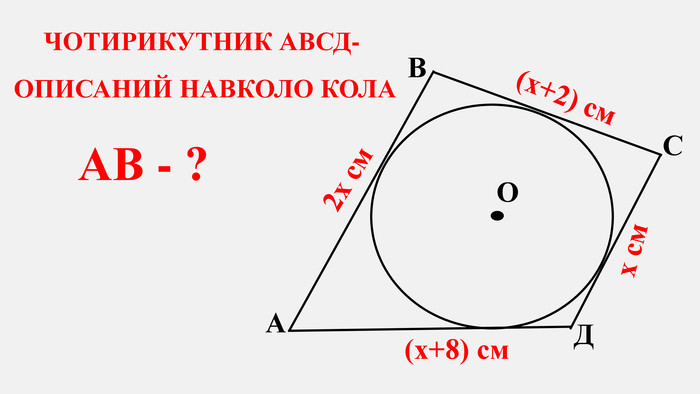






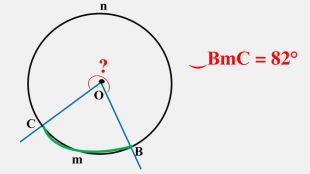
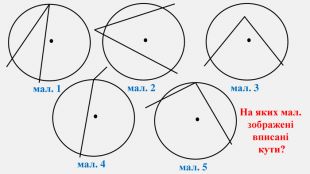
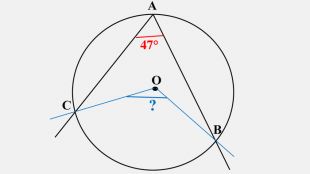
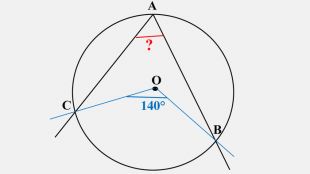
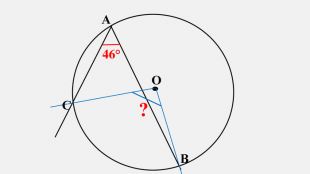
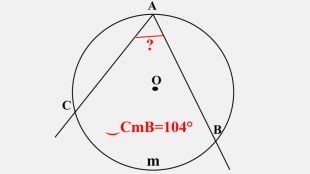
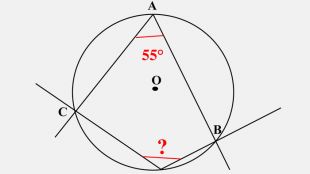
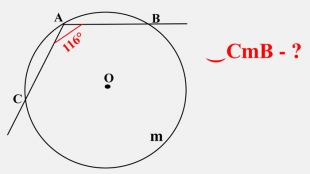
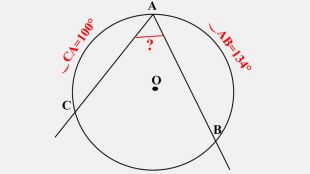
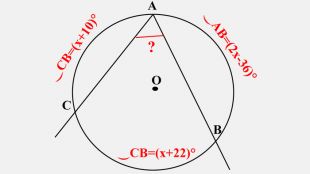
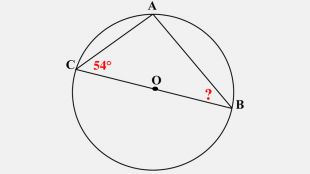
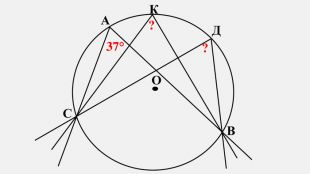
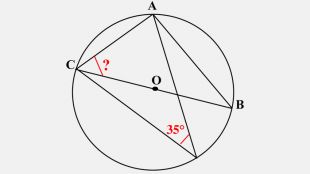
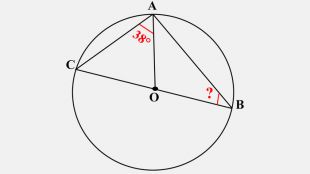
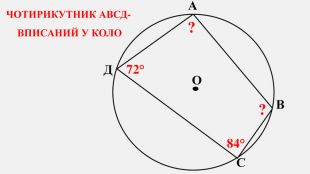
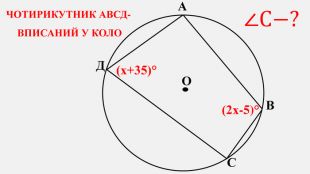
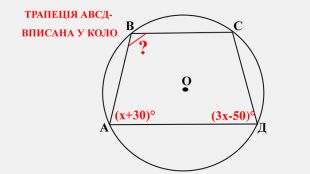
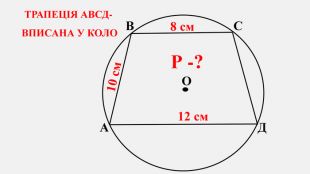
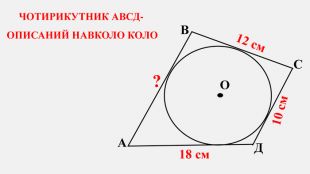
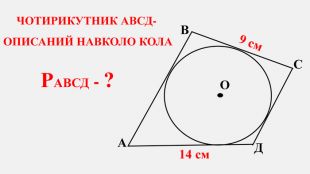
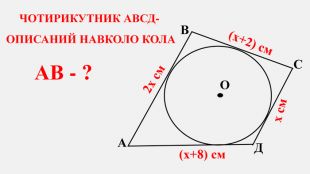


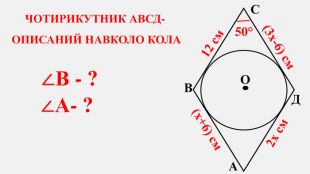



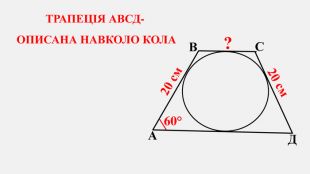
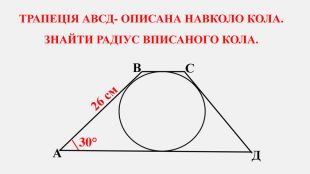
-

Будрик Оксана
20.11.2023 в 12:22
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Старостенко Світлана Богданівна
30.11.2022 в 10:51
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сидорчук Наталія
21.11.2022 в 22:48
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Забара Ольга
18.10.2021 в 14:07
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 1 відгук