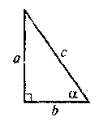
Тригонометричні функції гострого кута прямокутного трикутника. Розв’язування задач
Клас 8 Дата____________________
Тема. Тригонометричні функції гострого кута прямокутного трикутника. Розв’язування задач
Мета: домогтися засвоєння учнями змісту означень синуса, косинуса, тангенса і котангенса гострого кута прямокутного трикутника та їх властивостей, що випливають із теореми Піфагора, подібності прямокутних трикутників та властивостей сторін прямокутного трикутника (проти більшої сторони лежить більший кут, і навпаки). Сформувати вміння відтворювати зміст означень та їх властивостей, а також знаходити значення тригонометричних функцій гострого кута за даними прямокутного трикутника.
Наочність та обладнання: конспект «Означення тригонометричних функцій гострого кута».
Хід уроку
І. Організаційний етап
II. Перевірка домашнього завдання
III. Формулювання мети і завдань уроку
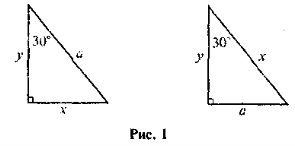Внауці і техніці часто розв'язують задачі, в яких за відомими стороною і кутом прямокутного трикутника треба знайти невідомі його сторони і кути, або навпаки, знаючи сторони прямокутного трикутник, обчислити його кути. Прикладом таких задач є добре відомі задачі на застосування співвідношень між катетом, що лежить проти кута 30°, і гіпотенузою, рисунки до яких подані нижче (див. рис. 1).
Знайдіть х, у, якщо а — відоме.
IV. Актуалізація опорних знань
Виконання усних вправ
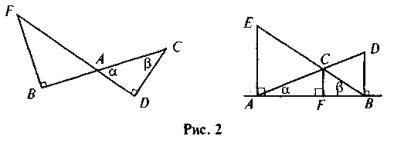
На рис. 2 знайдіть усі пари подібних прямокутних трикутників і доведіть їх подібність. У кожному трикутнику назвіть найменший катет та кут, що лежить проти цього катета, а також кут, що є прилеглим до цього катета.
V. Засвоєння знань
Домогтися розуміння учнями змісту вивченого матеріалу та його закріплення можна шляхом виконання вправ (див. нижче), запропонованих учням під час вивчення нового матеріалу.
-
Один з учнів 8 класу накреслив на дошці прямокутний трикутник із катетами 30 см і 50 см та обчислив значення синуса, косинуса, тангенса і котангенса гострого кута, що лежить проти меншого катета. Потім до дошки вийшов інший учень і сказав, що накреслить прямокутний трикутник із катетами 45 см і 75 см, у якому синус, косинус, тангенс і котангенс гострого кута, протилежного до найменшого катета, будуть більшими, бо його трикутник більший. Чи не помиляється цей восьмикласним? У чому його помилка?
- Які з чисел:
1; 0,5; 
; 
; 
; 
; 0; -0,3 можуть бути числовими значеннями синуса, косинуса, тангенса і котангенса гострого кута прямокутного трикутника? Поясніть.
-
Прочитайте записи: sin A =
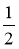; соs B = 
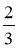; tg γ = 1; ctg φ = 2. Поясніть, що вони означають.
Після обговорення питань слід провести узагальнення способів застосування вивченого матеріалу, якщо треба знайти значення синуса, косинуса, тангенса і котангенса гострого кута прямокутного трикутника, то використовують означення цих понять; якщо ж треба відповісти на питання стосовно даних значень тригонометричних функцій, то слід використовувати їх властивості. У вивченні нового матеріалу користуємося конспектом.
|
Конспект 21 |
|
|
Означення тригонометричних функцій гострого кута. Тригонометричні тотожності
Якщо 0 < α < 90° — гострий кут прямокутного трикутника, а — протилежний катет; b — прилеглий катет; с — гіпотенуза, то sin α = |
|
|
Властивості 1) 0 < cos α < 1, 0 < sin α < 1, tg α > 0, ctg α > 0. 2) Якщо 0 < α < β < 90°, то sin α < sin β, cos α > cos β, tg α < tg β. 3) Якою α = β, то sin α = sin β, cos α = cos β, tg α = tg β, сtg α = ctg β. |
|
|
Тригонометричні тотожності |
|
|
1) sin2α + cos2α = 1 =>
2) |
|
, cos α = 
, tg α = 
, ctg α = 
.
, 
;
, 
, tg α · ctg α = 1.
VI. Формування первинних умінь
Виконання усних вправ
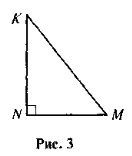
- За рисунком 3 визначте, яка тригонометрична функція кута К виражається відношенням:
а) 
; б) 
; в) 
.
- У прямокутному трикутнику KMN (рис. 3) KN > MN. Який із гострих кутів трикутника має більший синус; більший косинус; більший тангенс?
-
Чи може синус гострого кута прямокутного трикутника дорівнювати 0,99;
, 
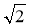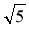– 2?
- Чи може добуток синуса і косинуса одного кута дорівнювати одиниці? А добуток тангенса і котангенса?
-
Чи може тангенс гострого кута прямокутного трикутника дорівнювати
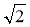; 0,01; 100?
Виконання письмових вправ
- Накресліть за допомогою транспортира прямокутний трикутник із гострим кутом 40°. Виміряйте його сторони та обчисліть синус, косинус і тангенс цього кута.
- Побудуйте прямокутний трикутник ЛИС, в якому:
а) tg А = 
; б) sin А = 
.
- Побудуйте кут 75°. За допомогою додаткових побудов і вимірювань знайдіть синус, косинус, тангенс і котангенс цього кута.
- Побудуйте гострий кут ос, якщо:
a) sin α = 
; б) cos α = 
.
- Доведіть, що для будь-якого гострого кута A tg A > sin A.
- Катеті гіпотенуза прямокутного трикутника відповідно дорівнюють 6 см і 10 см. Знайдіть:
а) синус гострого кута, що лежить проти більшого катета;
б) косинус гострого кута, прилеглого до меншого катета;
в) тангенс гострого кута, що лежить проти більшого катета.
VII. Підсумки уроку
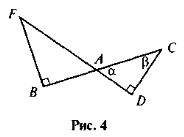
Подайте різними способами косинус, синус і тангенс кутів α і β (рис. 4).
VIII. Домашнє завдання
Вивчити зміст означень синуса, косинуса, тангенса гострого кута, прямокутного трикутника та доведення їх властивостей.
Розв'язати задачі.
- Накресліть гострий кут. Позначте на одній стороні кута дві точки і проведіть із них перпендикуляри до іншої сторони кута.
а) Виміряйте сторони прямокутних трикутників, що утворилися, та обчисліть двома способами синус побудованого кута. Порівняйте
результати.
б) Обчисліть косинус побудованого кута двома способами — за означенням і за основною тригонометричною тотожністю. Порівняйте результати.
- Катети прямокутного трикутника дорівнюють 8 см і 15 см. Обчисліть синус, косинус і тангенс найменшого кута трикутника.
- Висота рівнобедреного трикутник, проведена до основи, дорівнює 5 см, а довжина основи — 24 см. Знайдіть синус, косинус, тангенс і котангенс кута при основі трикутника.
про публікацію авторської розробки
Додати розробку