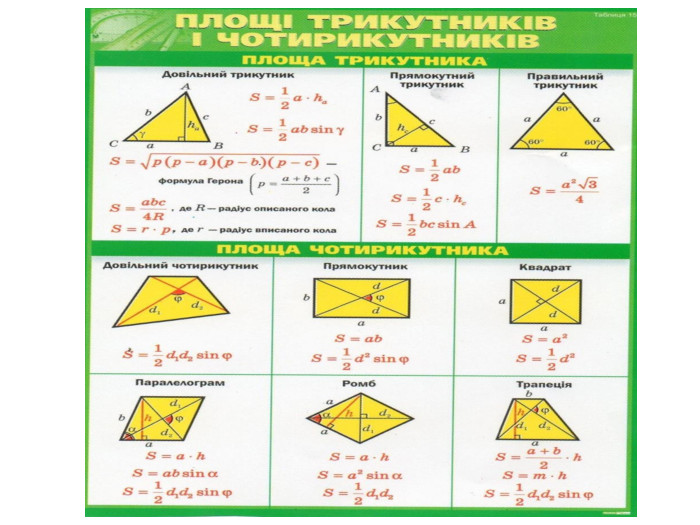
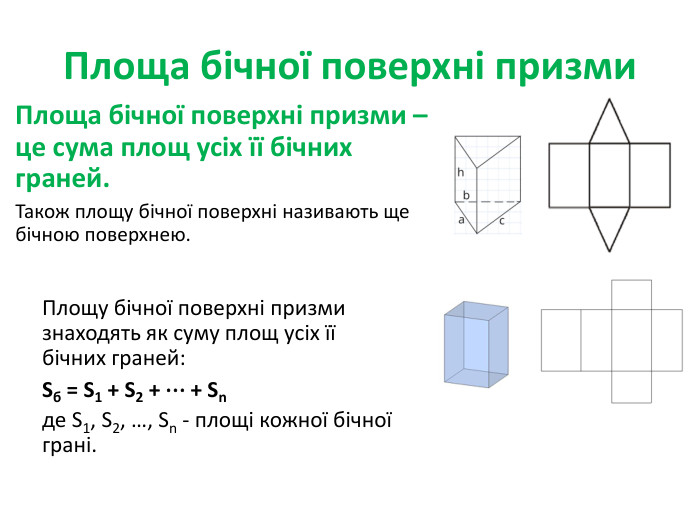
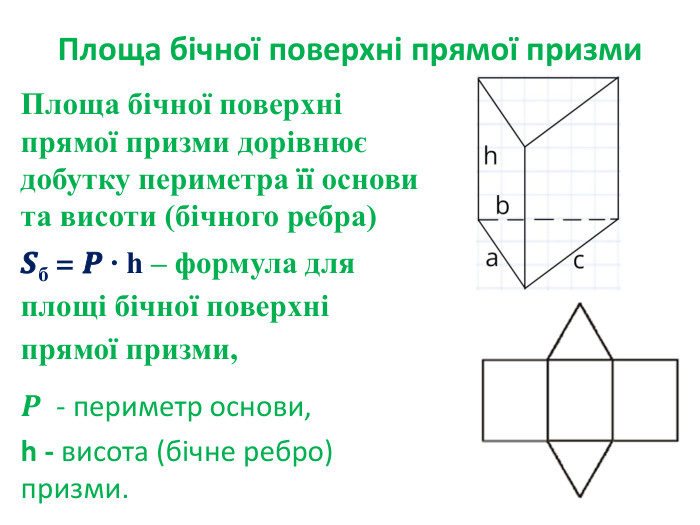
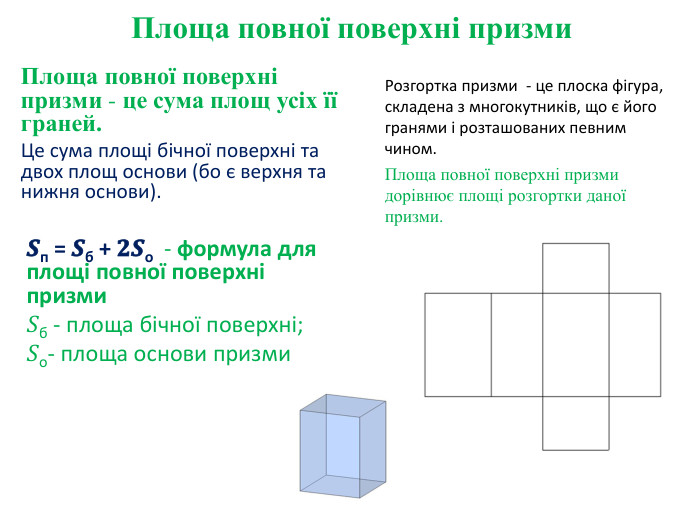
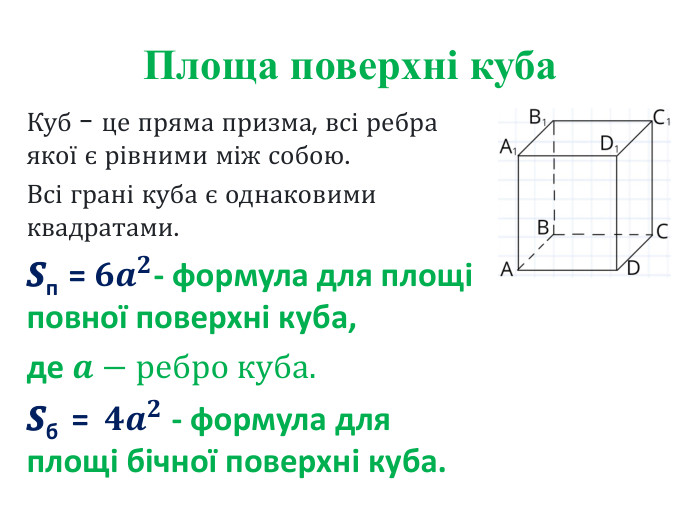
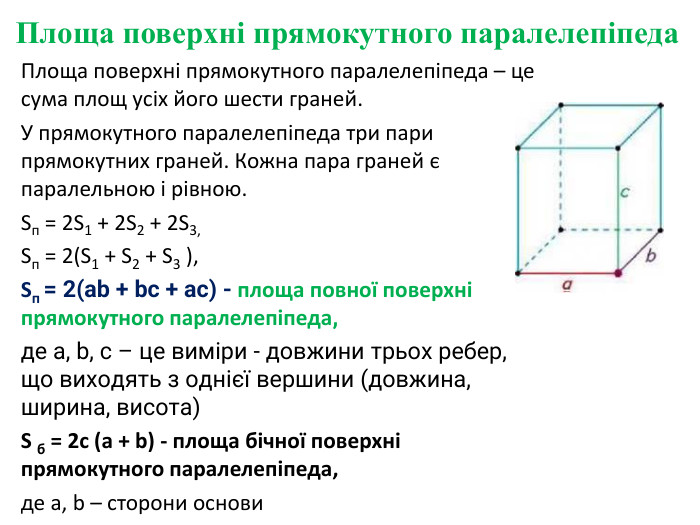
Площа повної та бічної поверхні призми
Про матеріал
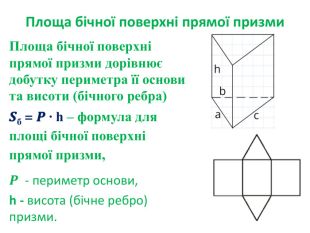
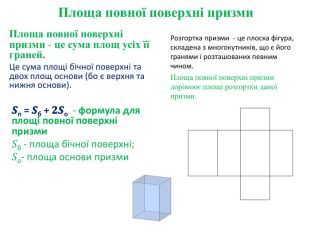
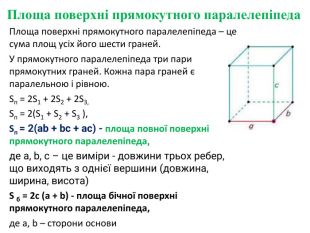
Тема уроку: Площа повної та бічної поверхні призми.
Урок засвоєння нових знань Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку