Задачі на комбінації піраміди та конуса

Про матеріал

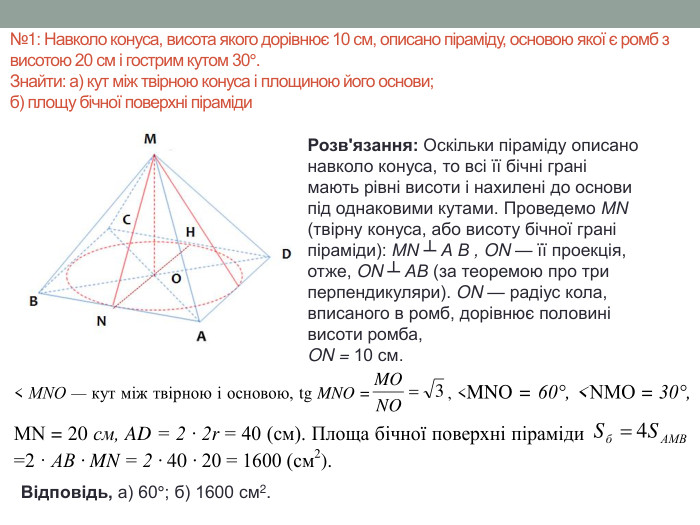
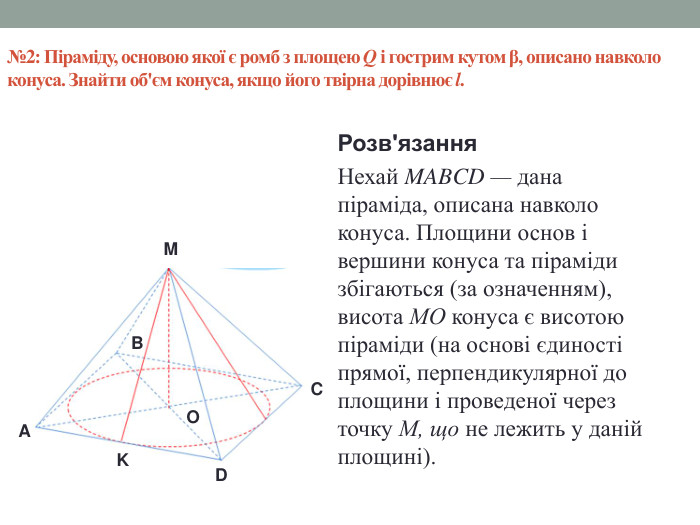
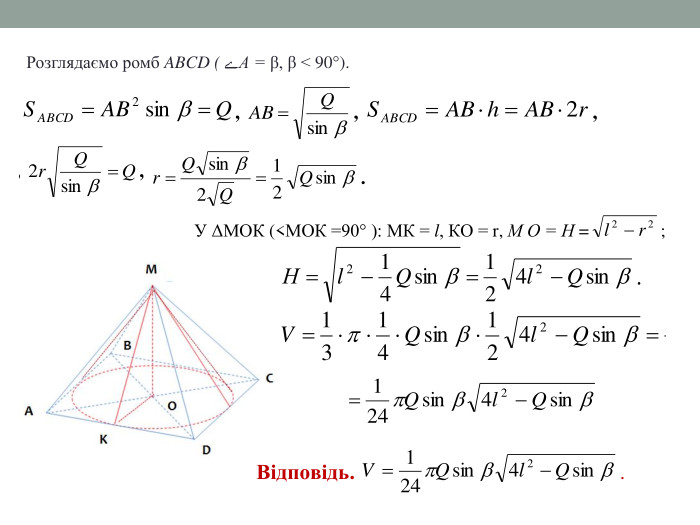
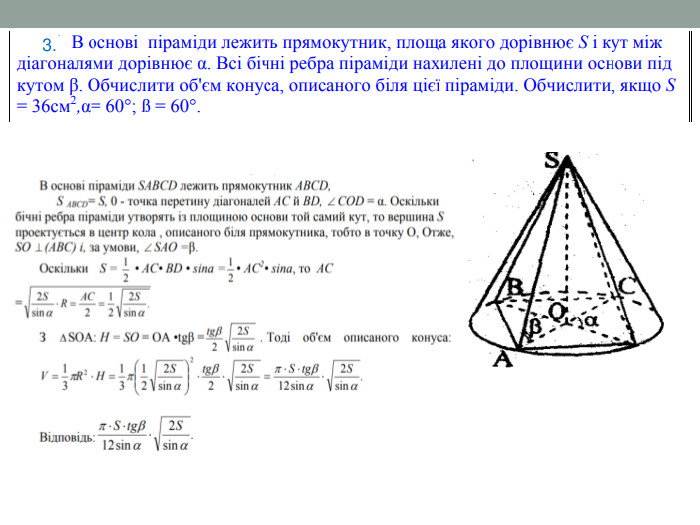
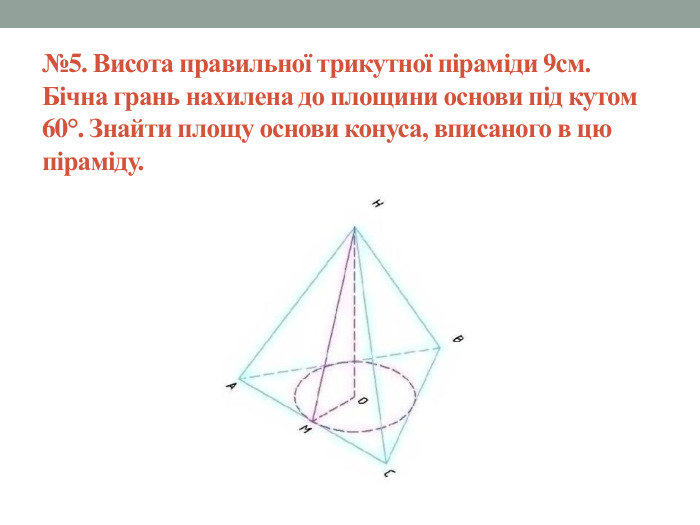
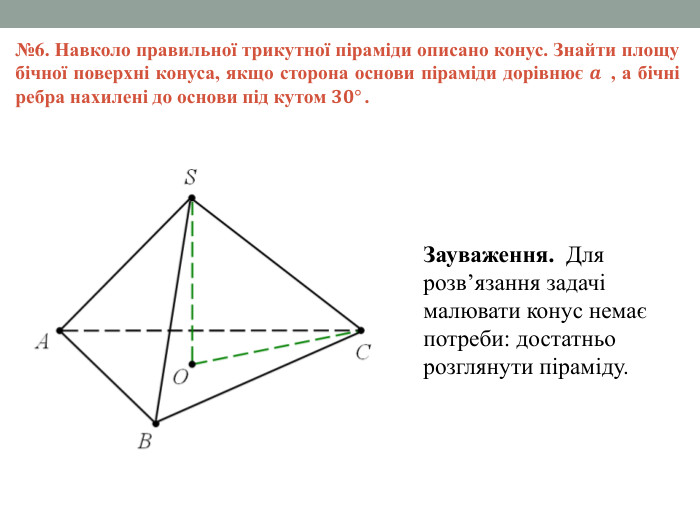
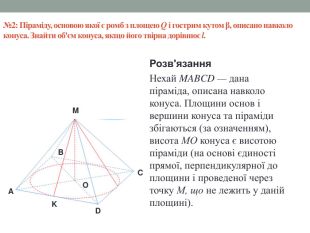
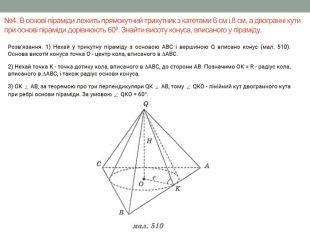
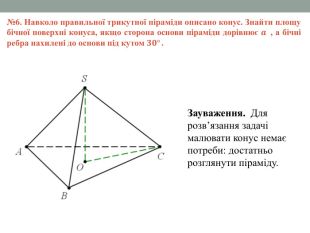
Матеріал містить задачі та розв'язки на комбінації піраміди і конуса в 11 класі. Мета: Навчити учнів розв'язувати задачі на знаходження об'ємів, площ бічних поверхонь, висоти та інших елементів піраміди та конуса, що входять до комбінації. Відпрацювати навички застосування теорем та формул, що стосуються пірамід та конусів.

Перегляд файлу

Попередній слайд 1 / 13 Наступний слайд

Зміст слайдів

Номер слайду 1

Задачі на комбінації піраміди і конуса

Номер слайду 2

№1: Навколо конуса, висота якого дорівнює 10 см, описано піраміду, основою якої є ромб з висотою 20 см і гострим кутом 30°. Знайти: а) кут між твірною конуса і площиною його основи;б) площу бічної поверхні піраміди. Розв'язання: Оскільки піраміду описано навколо конуса, то всі її бічні грані мають рівні висоти і нахилені до основи під однаковими кутами. Проведемо ΜΝ (твірну конуса, або висоту бічної грані піраміди): ΜΝ ┴ А В , ON — її проекція, отже, ON ┴ АВ (за теоремою про три перпендикуляри). ON — радіус кола, вписаного в ромб, дорівнює половині висоти ромба, ON = 10 см. Відповідь, а) 60°; б) 1600 см2.

Номер слайду 3

№2: Піраміду, основою якої є ромб з площею Q і гострим кутом β, описано навколо конуса. Знайти об'єм конуса, якщо його твірна дорівнює l. Розв'язання. Нехай MABCD — дана піраміда, описана навколо конуса. Площини основ і вершини конуса та піраміди збігаються (за означенням), висота МО конуса є висотою піраміди (на основі єдиності прямої, перпендикулярної до площини і проведеної через точку М, що не лежить у даній площині). MABKODC

Номер слайду 4

Об'єм V конуса обчислюємо за формулою: V= πr2Η, де r — радіус кола, вписаного у ромб ABCD, Н - висота конуса, Н = МО. Проведемо у площині АВС ОК AD, О - точка перетину діагоналей ромба – центр кола, вписаного у нього, ОК = r – радіус цього кола. Сполучимо точки М і К, МК ┴ AD (за теоремою про три перпендикуляри), МК — висота бічної грані піраміди.

Номер слайду 5

Розглядаємо ромб ABCD ( ﮮА = β, β < 90°).

Номер слайду 6

Номер слайду 7

№4. В основі піраміди лежить прямокутний трикутник з катетами 6 см і 8 см, а двогранні кути при основі піраміди дорівнюють 60º. Знайти висоту конуса, вписаного у піраміду.

Номер слайду 8

Відповідь: 23 см.

Номер слайду 9

№5. Висота правильної трикутної піраміди 9см. Бічна грань нахилена до площини основи під кутом 60°. Знайти площу основи конуса, вписаного в цю піраміду.

Номер слайду 10

Номер слайду 11

Зауваження. Для розв’язання задачі малювати конус немає потреби: достатньо розглянути піраміду.№6. Навколо правильної трикутної піраміди описано конус. Знайти площу бічної поверхні конуса, якщо сторона основи піраміди дорівнює 𝒂 , а бічні ребра нахилені до основи під кутом 𝟑𝟎° .