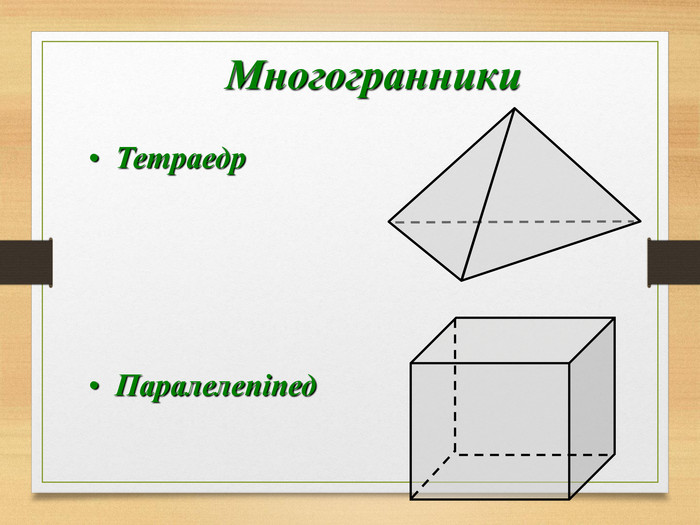
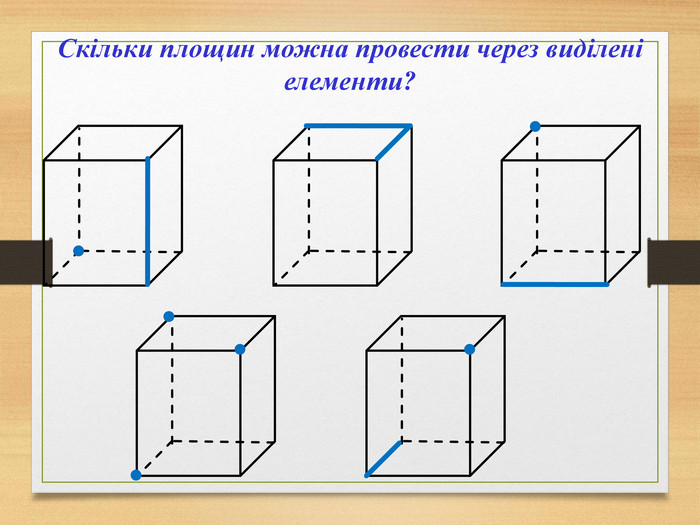
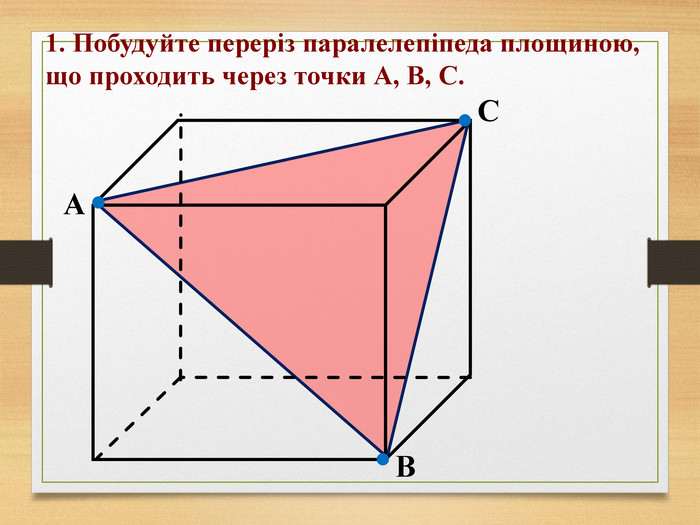
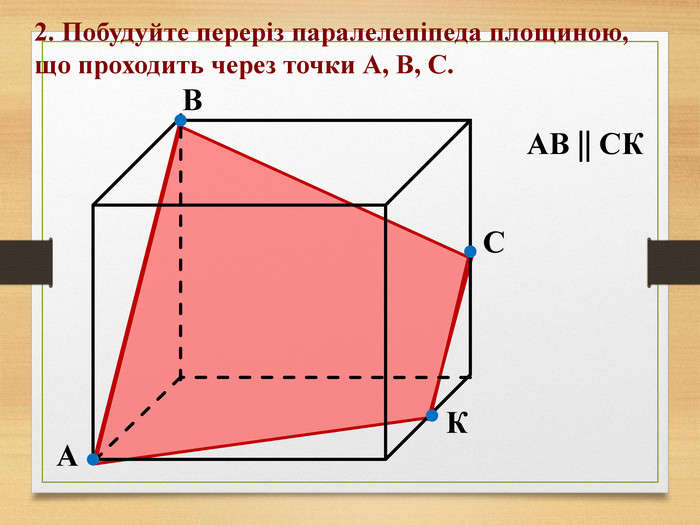
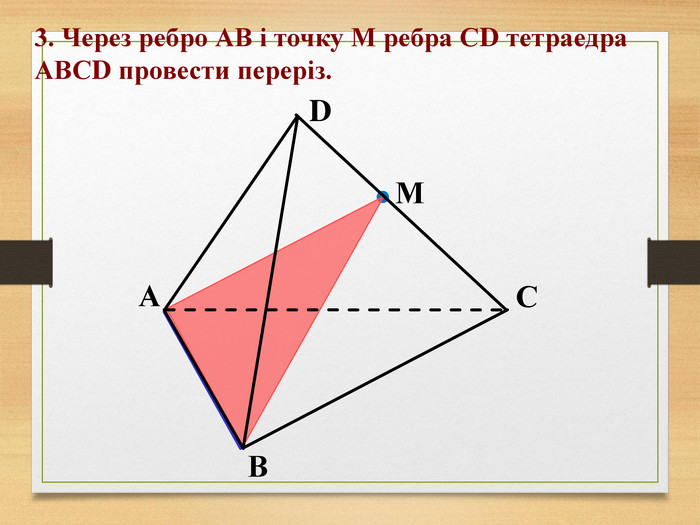
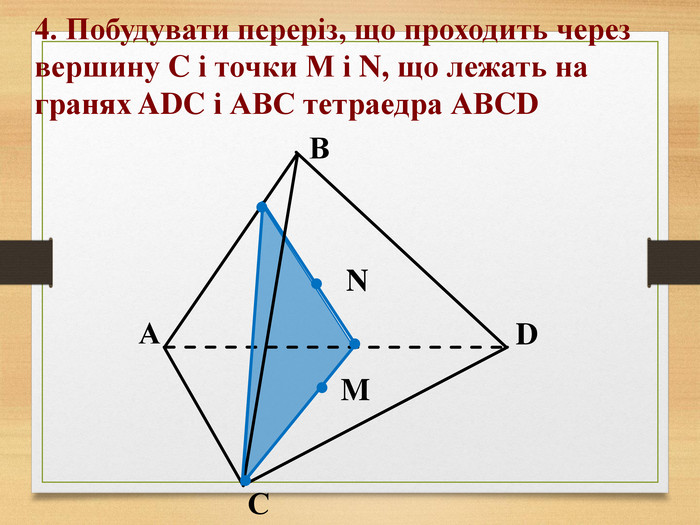
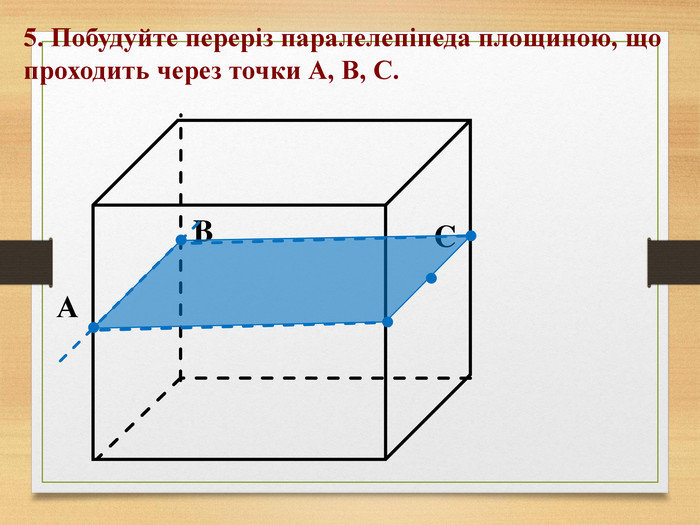
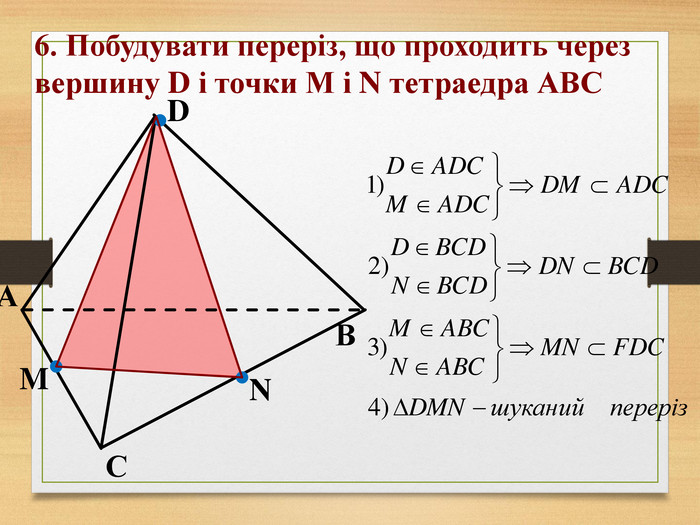
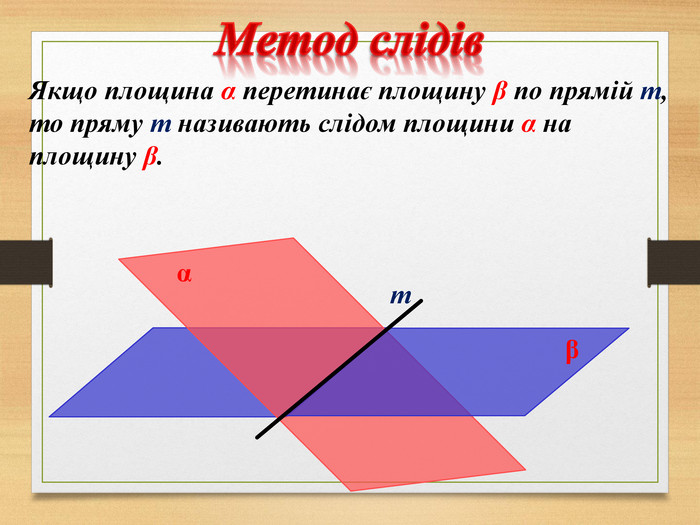
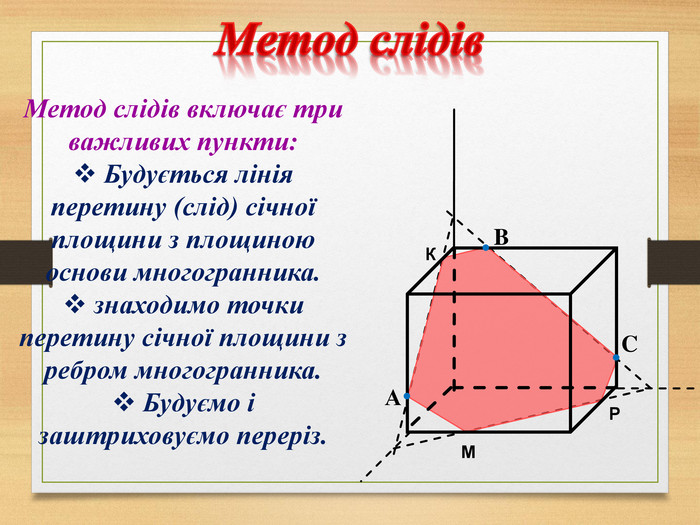
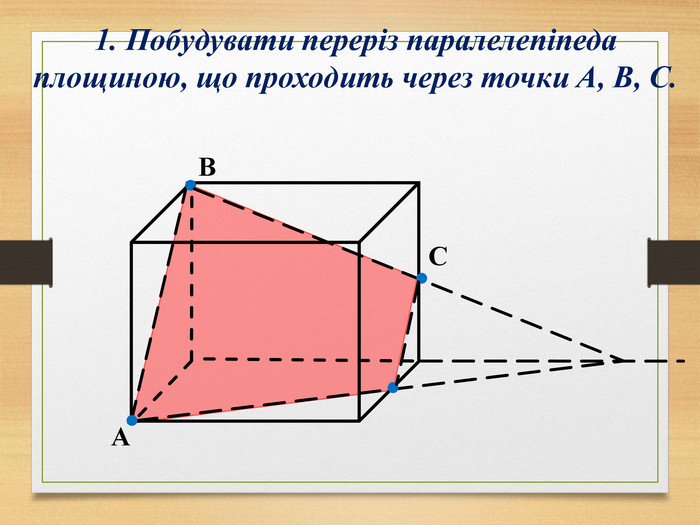
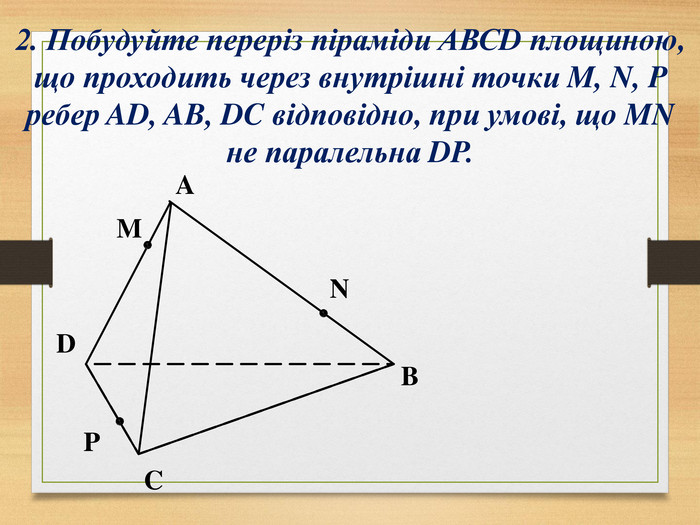
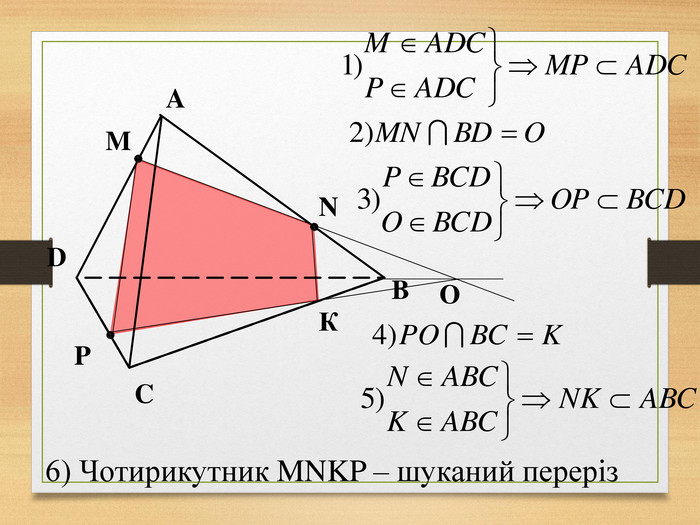
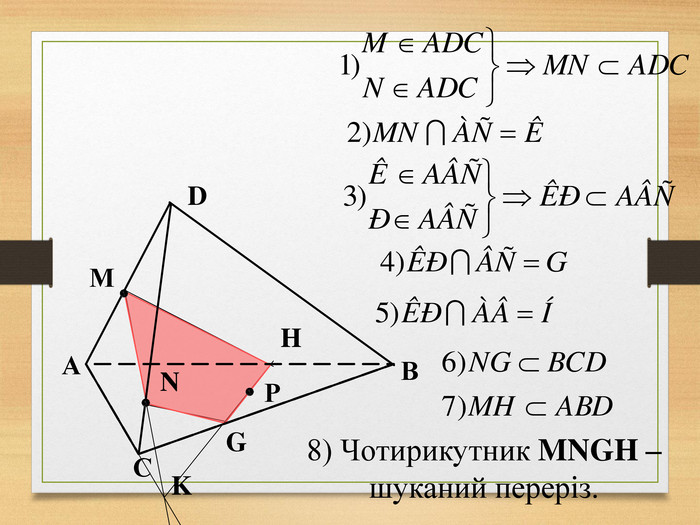
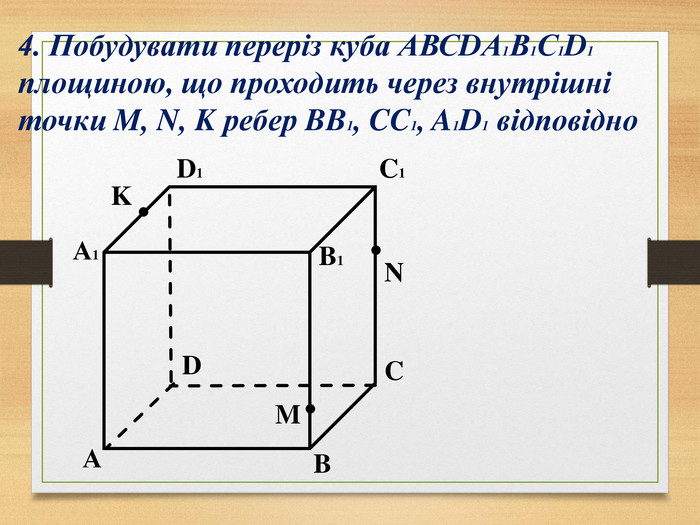
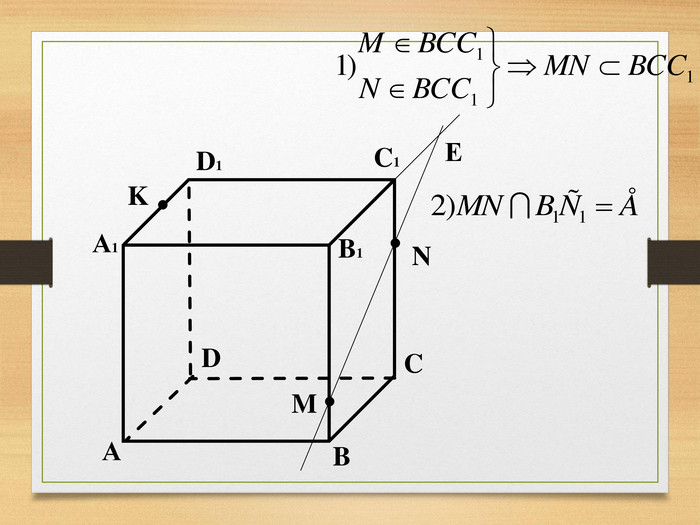
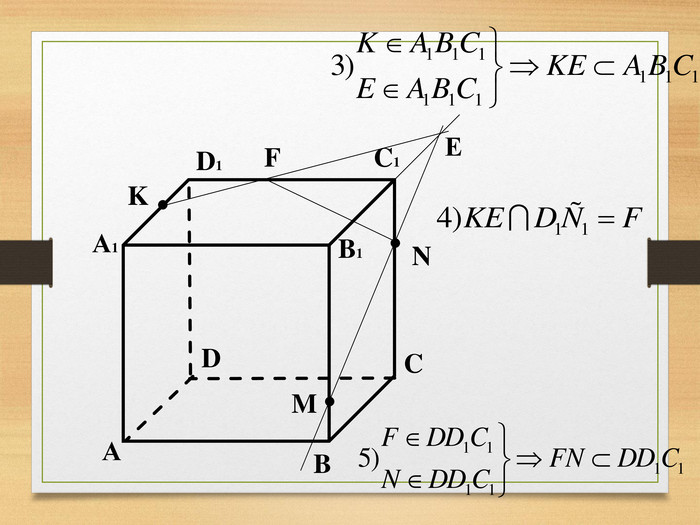
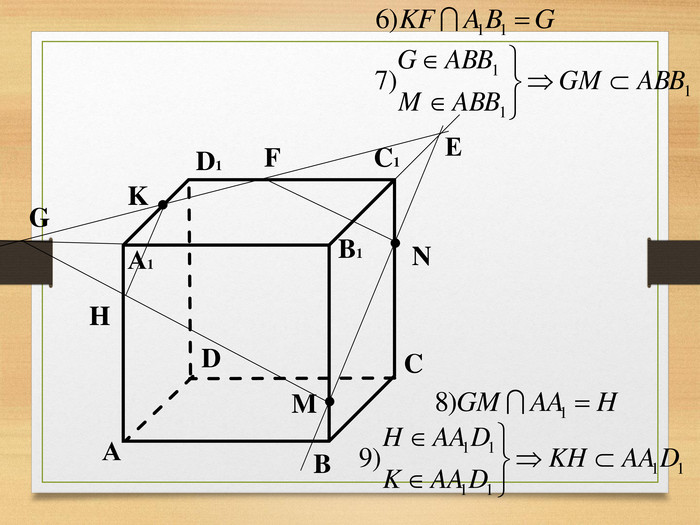
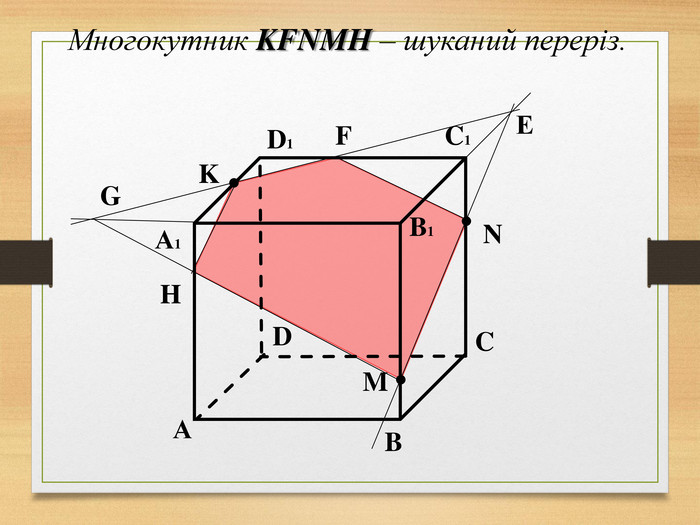
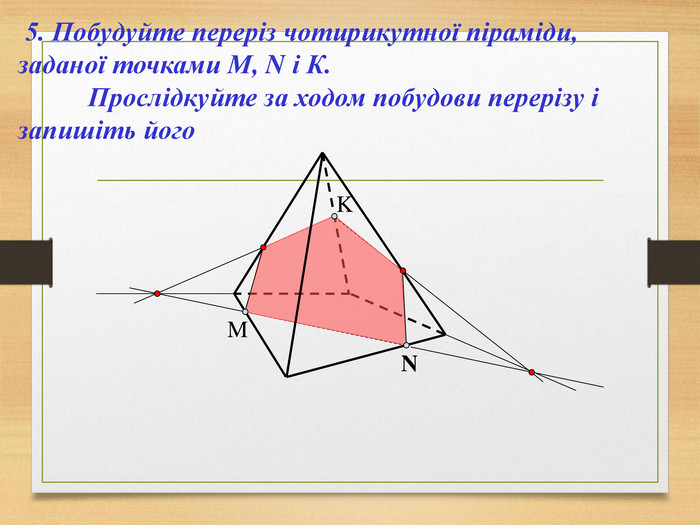
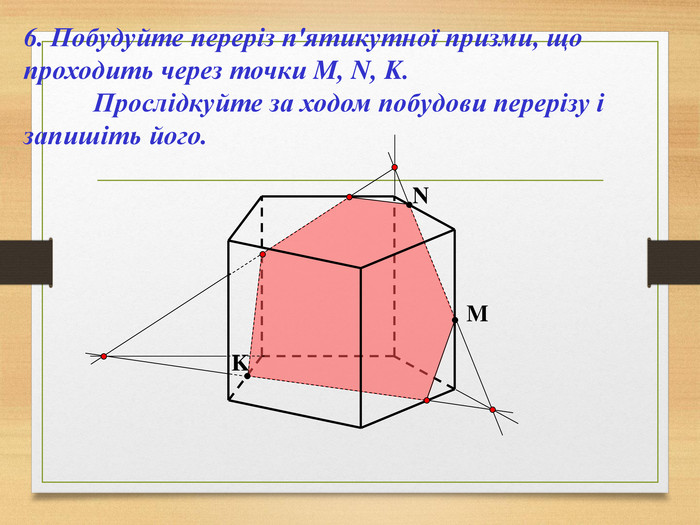
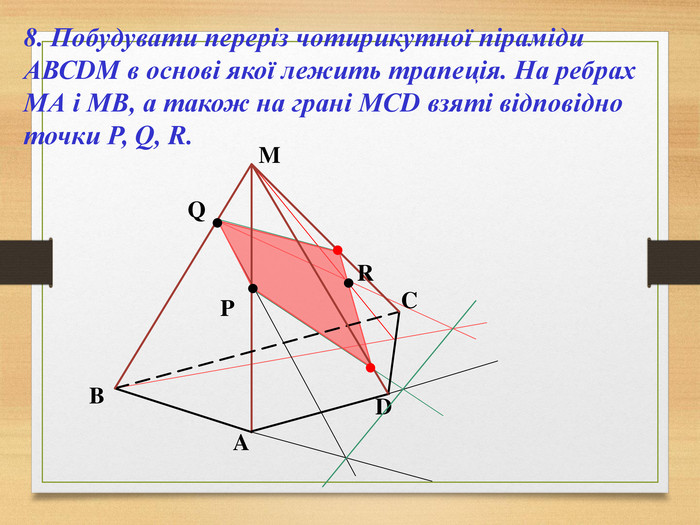
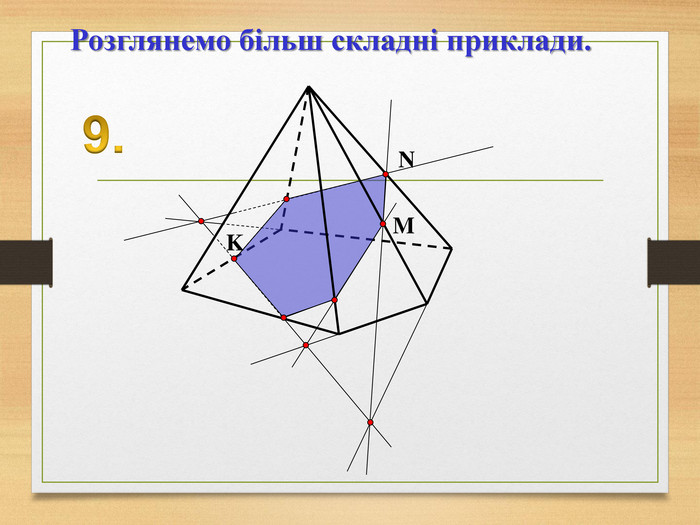
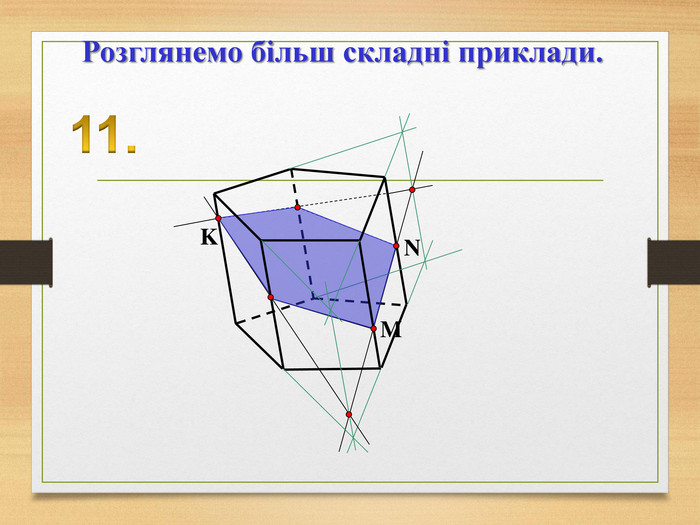
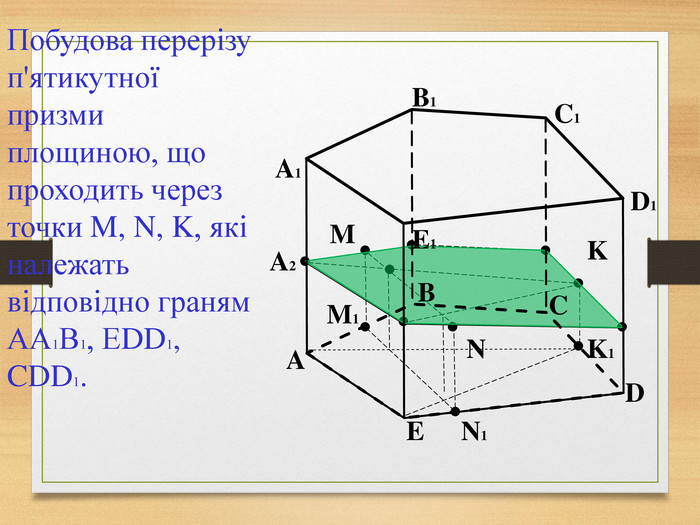
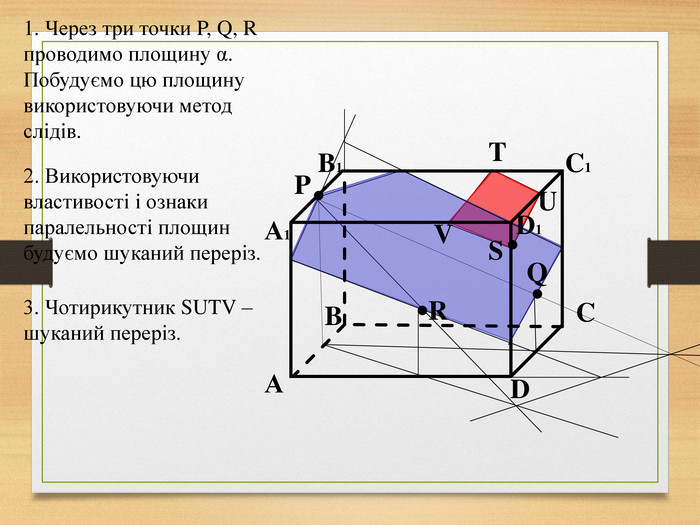
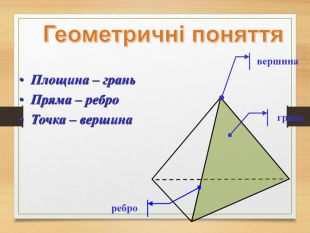
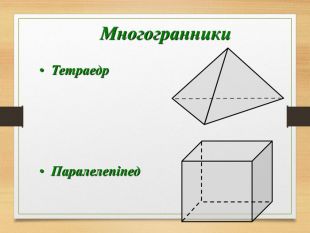
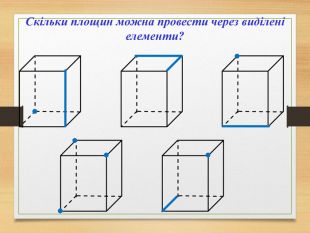
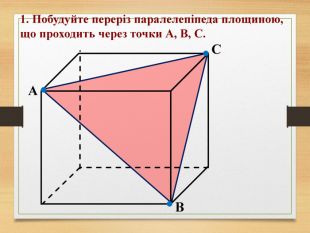
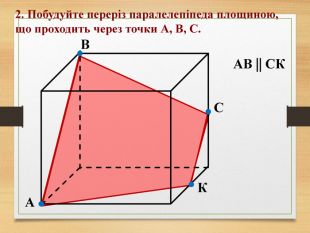
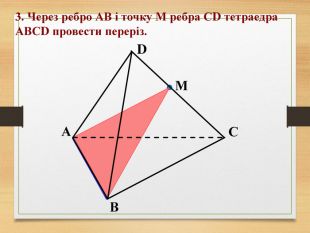
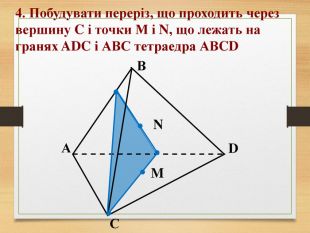
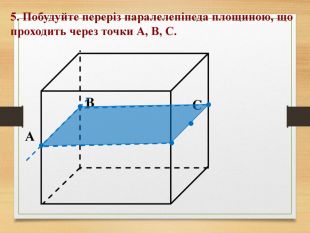
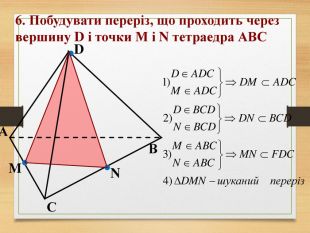
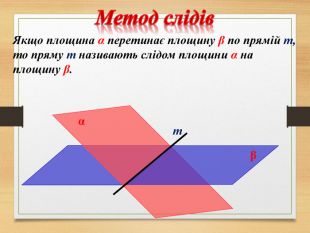
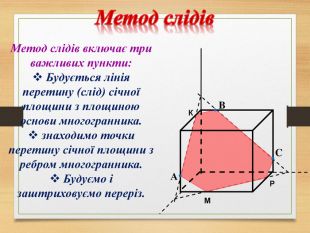
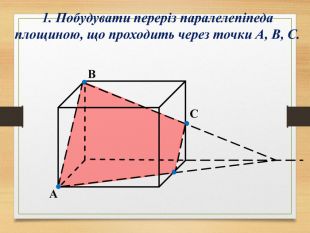
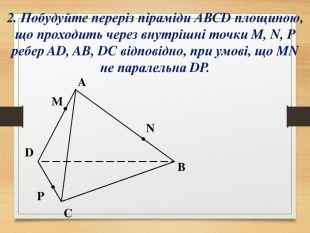
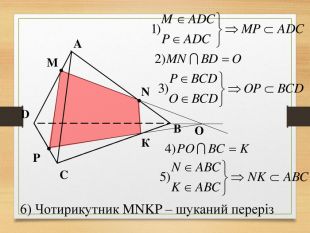
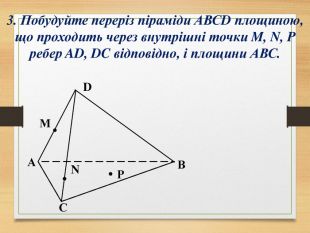
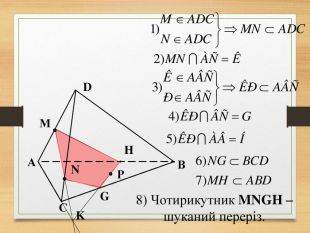
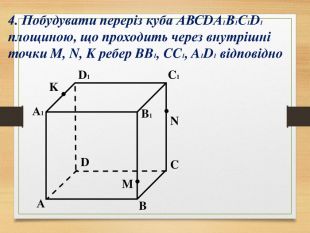
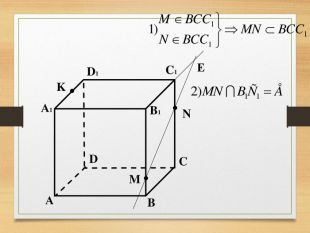
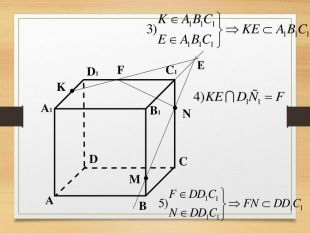
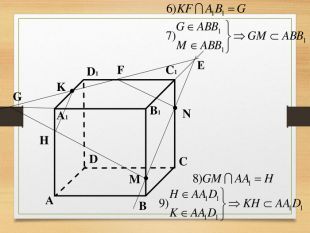
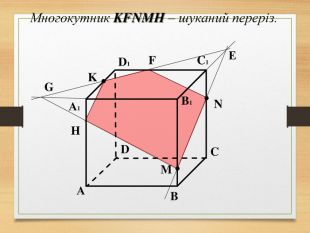
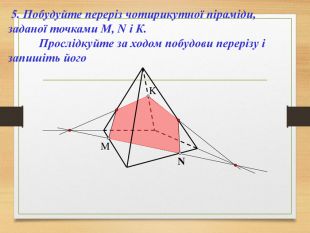
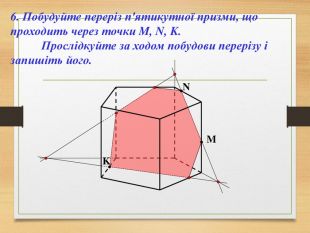
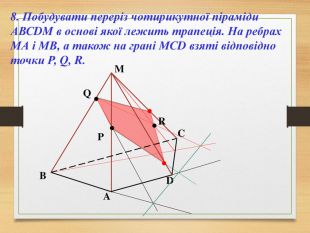
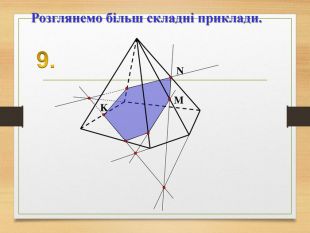
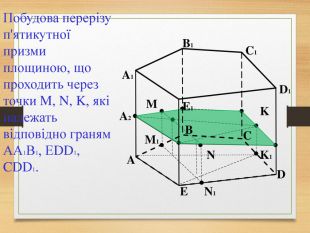
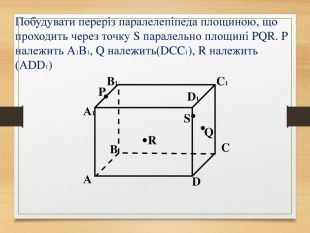
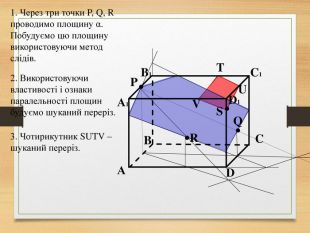
Побудова перерізів многогранників
Про матеріал
Пропоную до уваги презентацію до уроків геометрії з теми "Перерізи многогранників". Презентація унаочнює, візуалізує навчальний матеріал, зацікавлює учнів, мотивує до навчання. Буде корисною для вчитеів та учнів. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Дуже дякую)
ppt
До підручника
Геометрія (профільний рівень) 10 клас (Бевз В.Г., Бевз Г.П., Владімірова Н.Г., Владіміров В.М.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку