Урок "Вектори у просторі. Vectors in space"

Славутський навчально-виховний комплекс

« Спеціалізована школа І-ІІІ ступенів, ліцей « Успіх »

Конспект   уроку       на тему

розробила

вчитель математики

       Шелестюк А.О.

2019 – 2020 н.р.

Тема: Вектори у просторі. Vectors in space

( з елементами англійської мови )

Мета:

навчальна: Узагальнити й систематизувати матеріал з теми « Декартові координати і вектори у просторі»; Повторити вивчений матеріал: формули, означення, властивості;

формувати вміння учнів застосовувати вивчені означення та властивості до

розв’язування задач

розвивальна: розвивати логічне мислення, уміння правильно висловлювати свою думку, навички    розв’язувати задач на обчислення координат векторів та виконання дій із векторами;

виховна: виховувати інтерес до вивчення математики, творчу активність, уважність,  охайність при зображенні геометричних фігур; популяризація англійської мови.

Тип уроку: узагальнення й систематизація знань, умінь та навичок.

Наочність та обладнання: набір демонстраційного креслярського приладдя; таблиця «Вектори у просторі», комп’ютер, комп’ютерний проектор,  презентація теми з комп’ютерною підтримкою Microsoft Office Power Point.

Все навколо – геометрія

Ле Корбюзі

All around - geometry

Le Corbusier

ХІД УРОКУ

І. Організаційний етап  

Сьогодні ми проведемо незвичний урок з математики, оскільки будемо частково говорити та читати  англійською мовою. 

II. Повідомлення теми, мети уроку.

Сьогодні наш урок -  урок - подорож. Подорож до країни – Математика. Нам необхідно проїхати складним маршрутом, долаючи на своєму шляху різні перешкоди. Мета нашої подорожі – систематизувати знання з теми «Декартові координати і вектори у просторі», удосконалити навички розв’язування різних задач, ви зможете ще раз впевнитись у необхідності вивчення даної теми

ІІІ. Мотивація навчальної діяльності.

Подорож наша буде проходити через такі країни:

•                               теоретична
•                               перевір себе
•                               точних обчислень
•                               застосування
•                               привал

ІV Перевірка домашнього завдання

Учитель  відповідає на питання учнів  стосовно домашнього завдання.

V. Відтворення та коригування опорних знань.

Актуалізація опорних знань

1. Метод «Хмари»

Асоціація слова «Вектор»

https://drive.google.com/drive/my-drive

Учні дають свої відповіді.

2. Гра «Математичне доміно»

Є набір карток двох кольорів. На одних записується початок речення, на інших

його закінчення

3. Графічний диктант

Назвіть знайомі вам з курсу геометрії 7 класу геометричні фігури, зображені на рисунку.

1. ( Показуються фігура, а учні пишуть її назву)

1) А.                2)      а            3)  С .                . Д      4)       О.                  А

5)               6)

7) В

   А

Відповіді:  1 – точка, 2 – пряма,  3 – відрізок,   4 – промінь, 5 – кут,

 6 – замкнена ламана   7- напрямлений відрізок ( вектор)

Answers: 1 – point,  2 - straight, 3 – segment,  4 - beam, 5 - the angle,

  6 - closed broken     7- directional segment (vector)

2.Учні відповідають на запитання

Які властивості цих фігур ви знаєте?

What properties do you know about these figures?

метод «Мікрофон».

3. Назвіть елементи вектора

6. Виконання практичних завдань на повторення й

                                    закріплення основних умінь і навичок.

Країна точних обчислень

1. Тести

1.Дано точки A(3; −1; 1) і B(5; 1; 1). Знайдіть координати вектора .

( Find the coordinates of the vector.)

А) (0; -1; 2); Б) (−2; −2; 0); В) (4; 0; 1); Г) (-2; 0; 0) Д) (2; 2; 0)

      2. Дано вектор (−2;5;1). Які координати має вектор ?

(What are the coordinates of the vector ?

А) (2; −5; −1); Б) (2; 1; 5); В) (2; −5; 1); Г ( 2; 5;-2) Д) неможливо  визначити

3. Знайдіть координати вектора ( Find the coordinates of the vector)    =  + , якщо  (2; 0; 1) ,  (5; 2; − 3) .
А) (7; 2; −2); Б) (7; 2; − 4); В) (7; − 2; −2); Г) (2; 7;-7); Д) неможливо .визначити

4. При якому  значенні n вектори 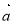 (10; 15; 20) і  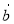(n; 3; 4) є колінеарними?
   ( are collinear?)
   А) 2    Б) 50    В) 5     Г) 12     Д) 0
5. При якому значенні х вектори 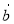 (10; 15; 20) і  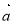(х; 3; 4) є перпендикулярні?
   ( are perpendicular?)
   А) 20     Б) -20      В) -14,5      Г) 114,5         Д) 0

2. Розв’язування вправ

№1

Знайдіть координати вектора =  -2, якщо (2; 0; -6) ,  (-1; 2; − 3).

№2

Зобразіть на рисунку взаємне розміщення точок А, В, С, якщо

А) = 3;      Б) = -2;    В) = .

№3

Зобразіть тетраедр ABCD та вектор, що дорівнює -+.

3. РУБРИКА « ЗАСТОСУЙТЕ НА ПРАКТИЦІ»

“APPLY INTO PRACTICE”

ЗАДАЧА 1.

Щоб зважити брусок вагою 10 Н за допомогою двох динамометрів, розрахованих

на вимірювання сили 5 Н, діють так. обидва динамометри укріплюють поряд на

одному рівні, а брусок підвішують одразу до обох гачків динамометрів. Поясніть,

чому так можна зважити брусок. Перевірте експериментально. ( необхідне

обладнання лежить на партах у кожної групи ) 

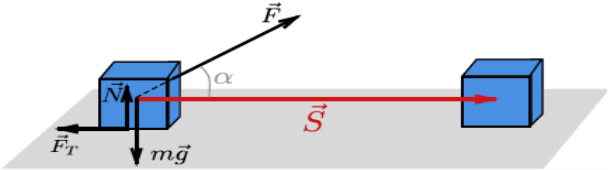
ЗАДАЧА 2.

Малюк тягне санки із силою 10Н на відстань 20 метрів. Кут між напрямом сили і

напрямом переміщення 45⁰. Яку роботу виконав малюк, перетягуючи санки?

VІІ. Підсумок уроку

Застосування векторів

Application of vectors

 Планування будинку за допомогою векторної графіки

За допомогою поняття "вектор" і вміння застосовувати його властивостііснує майже все, що створила людина. Без векторів не існувало б будівництво, усі будівлі були б криві, непропорціональні та швидше за все, не було б змоги створити їх взагалі.
 

Planning a house with vector graphics

With the concept of "vector" and the ability to apply its properties, there is almost everything created by man. Without vectors there would be no construction, all buildings would be crooked, disproportionate and most likely, it would not be possible to create them at all.    Planning a house with vector graphics.

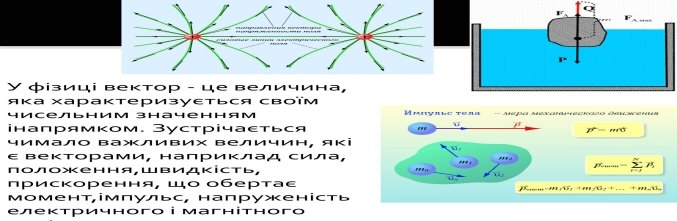
У фізиці

У фізиці вектор - це величина, яка характеризується своїм чисельним значенням інапрямком. Зустрічається чимало важливих величин, які є векторами, наприклад сила, положення,швидкість, прискорення, що обертає момент,імпульс, напруженість електричного і магнітного полів. 

In physics

In physics, a vector is a quantity that is characterized by its numerical value and direction. There are many important quantities, which are vectors, such as force, position, velocity, torque, momentum, momentum, intensity of electric and magnetic fields.

Комп‘ютерна графіка

Комп‘ютерна графіка   50% програм і комп`ютерних ігор

Computer Graphics
Computer graphics 50% of applications and computer games

Національна українська вишивка

Векторні фони на тему національної української вишивки з яскравим і барвистим геометричним і рослинним орнаментом, що застосовуються для вишивання рушників та одягу.

National Ukrainian Embroidery

Vector backgrounds on the theme of national Ukrainian embroidery with bright and colorful geometric and floral ornaments are used for embroidery of towels and clothing.

ІХ. Домашнє завдання

1. Розв’язати задачу

Троє учнів намагаючись зрушити з місця вантаж, тягнуть його кожен у свою

сторону з однаковою силою 100Н. які кути між напрямами їхніх сил, якщо вантаж

не зрушив з місця? Як треба змінити ці напрями, щоб зрушити з місця вантаж?

( The three students, trying to remove the cargo, pull it into their own  side with equal force 100H. What are the angles between the directions of their forces, if the load  not moved? How should these directions be changed to shift the cargo?)

2. ( Творче ) самостійно скласти картки для гри в «математичне доміно» з теми

«Вектори» на англійській мові.