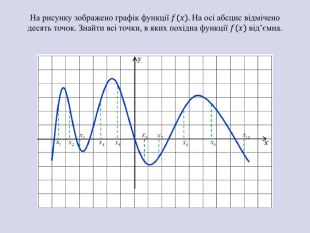
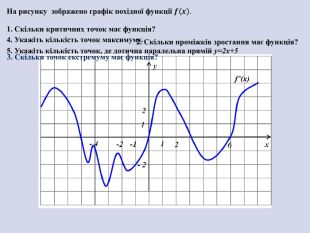
Презентація "Застосування похідної"
Про матеріал
Презентація може бути використана вчителями математики для підготовки до уроку з теми "Похідна". Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку



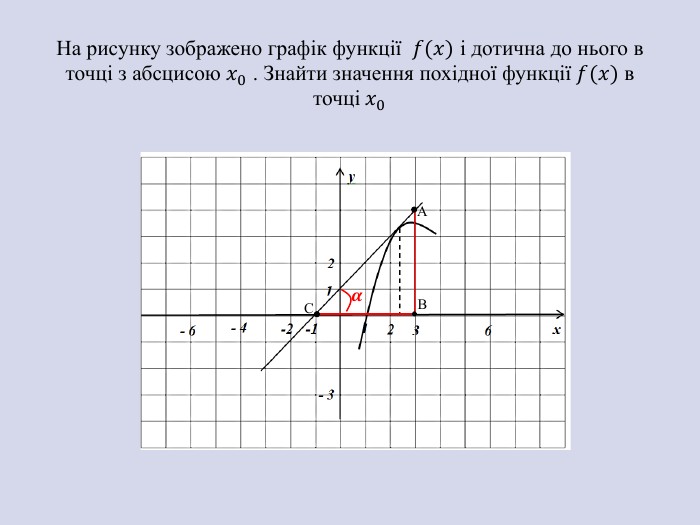
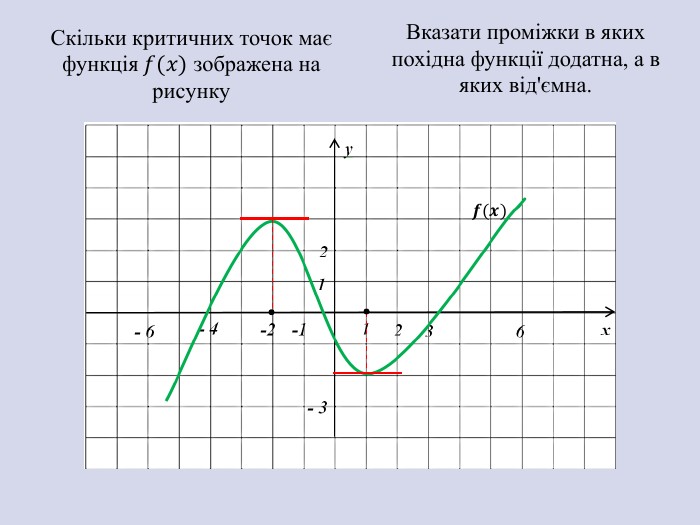

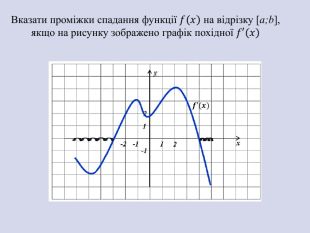
![Вказати проміжки спадання функції 𝑓𝑥 на відрізку [a;b], якщо на рисунку зображено графік похідної 𝑓′𝑥 𝒇′(𝒙) Вказати проміжки спадання функції 𝑓𝑥 на відрізку [a;b], якщо на рисунку зображено графік похідної 𝑓′𝑥 𝒇′(𝒙)](/uploads/files/1874777/332366/373808_images/6.jpg)
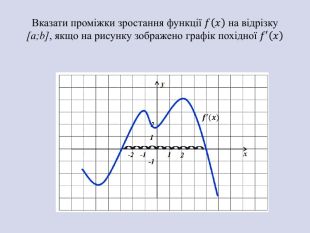
![Вказати проміжки зростання функції 𝑓𝑥 на відрізку [a;b], якщо на рисунку зображено графік похідної 𝑓′𝑥 𝒇′(𝒙) Вказати проміжки зростання функції 𝑓𝑥 на відрізку [a;b], якщо на рисунку зображено графік похідної 𝑓′𝑥 𝒇′(𝒙)](/uploads/files/1874777/332366/373808_images/7.jpg)
![Дослідити функцію та побудувати її графік𝑦=4𝑥3−3𝑥2 Знайти найбільше та найменше значення функції 𝑓𝑥=2𝑥3−9𝑥2+3 на проміжку [1;4] Дослідити функцію та побудувати її графік𝑦=4𝑥3−3𝑥2 Знайти найбільше та найменше значення функції 𝑓𝑥=2𝑥3−9𝑥2+3 на проміжку [1;4]](/uploads/files/1874777/332366/373808_images/9.jpg)