Похідна та її застосування

 Тема уроку.  Похідна та її застосування

розвивати пам'ять, логічне мислення учнів, вміння пояснювати свої дії;

виховувати    культуру    математичного    мовлення,     почуття товариськості, взаємовиручки.

Очікувані результати

Форма проведення уроку: «КВК»

Тривалість уроку: 45 хвилин.

Тип уроку: вироблення вмінь і навичок

Наочність: ПК, картки із завданнями.

 

 

Організація учнів

Учитель ділить клас на дві команди, призначає журі (4 учні), 2 асистенти. Готуючись до уроку КВК, учні обирають двох капітанів команд. Команди

підбирають назву, девіз, емблему, коротке представлення і готують домашні завдання.

Перед уроком кожна команда сідає окремо.

Хід уроку

I. Організаційний момент

Ведучим КВК є вчитель. Він оголошує тему уроку і правила перед кожним конкурентом, а також представляє членів журі та двох своїх асистентів.

Кожна команда демонструє свою назву, девіз, емблему.

(Максимальна оцінка - 6 балів).

II. Актуалізація опорних знань

(конкурс «Математичний аукціон» Учні відповідають лише за бажанням ),

Запитання аукціону

1. Що називається похідною функції в точці?

2.Сформулювати необхідну умову диференційованості функції в
точці .

3. В чому полягає геометричний зміст похідної?

 

(Якщо s = f(t) - рівняння прямолінійного руху матеріальної точки (твердого тіла), то швидкість цього руху в момент часу t дорівнює похідній від шляху за часом в деякий момент часу, тобто:

6. Сформулювати теорему про похідну суми (різниці) функцій.
7. Сформулювати теорему про похідну добутку функцій.
8. Сформулювати теорему про похідну частки функцій.
9. Сформулювати теорему про похідну складеної функції.

10. Сформулювати теорему Ферма

(Якщо неперервна функція у = f(х)в точці х₀ має екстремуми, то її похідна f цій точці дорівнює нулю або її не існує)

11.Сформулювати достатні умови екстремуму функції

18. Сформулювати схему дослідження функції неперервної на інтервалі

III. Перевірка домашнього завдання

(Конкурс «Розминка»)

Учні - асистенти роздають учням завдання для самостійної роботи і збирають аркуші з домашніми завданнями

Перевірка домашнього завдання (максимальна оцінка 4 бали).

Після звукового сигналу самостійна робота припиняється. На екрані виводяться правильні відповіді і учні перевіряють роботи суперників, підкреслюючи помилки. Аркуші збирають асистенти і передають членам журі.

Розв'язання домашнього завдання

І команда

1.  Дослідити функцію і побудувати її графік

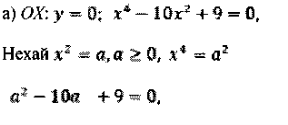
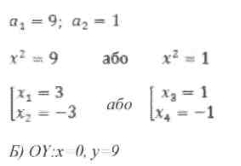
5. Дослідимо поведінку функції на кінцях області визначення проміжків

6. Для визначення проміжків монотонності знайдемо похідну заданої функції

Критичні точки

 

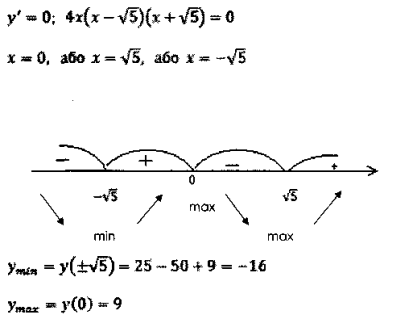
8. Визначимо проміжки опуклості заданої функції:

 

 

 

 

 

 

 

 

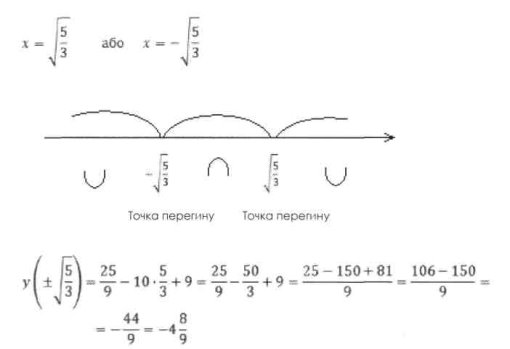
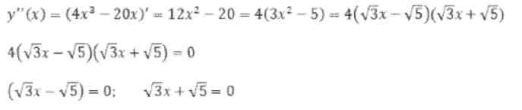
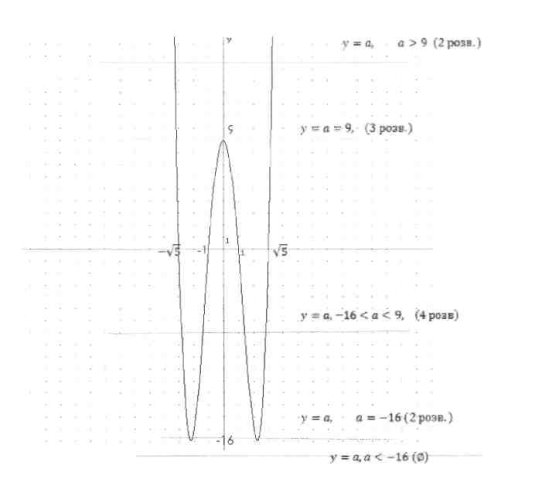
Домашнє завдання II команди

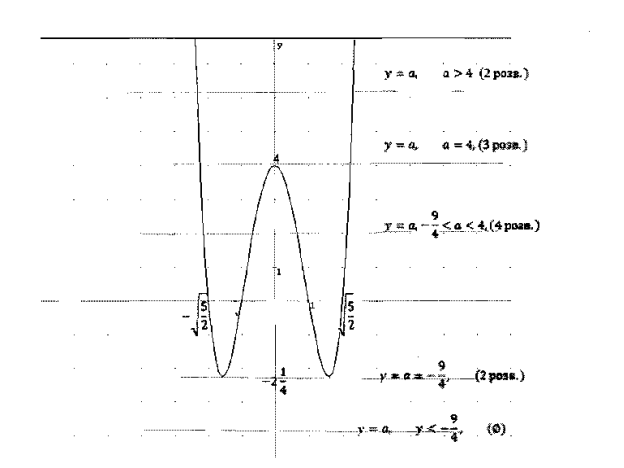
б) Вказати кількість коренів рівняння

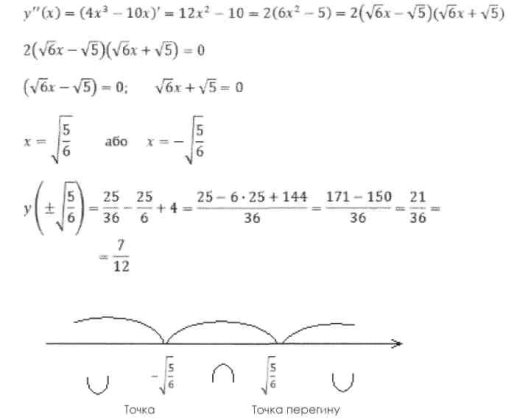
1. Дослідити функцію і побудувати її графік

1.                                                                                Областю визначення є вся числова пряма
2.                                                                                Функція парна, оскільки

Графік функції симетричний відносно осі ОУ

3. Функція неперіодична.

4. Знаходимо точки перетину графіка функції з осями координат

5. Дослідимо поведінку функції на кінцях області визначення проміжків

6. Для визначення проміжків монотонності знайдемо похідну заданої функції

 

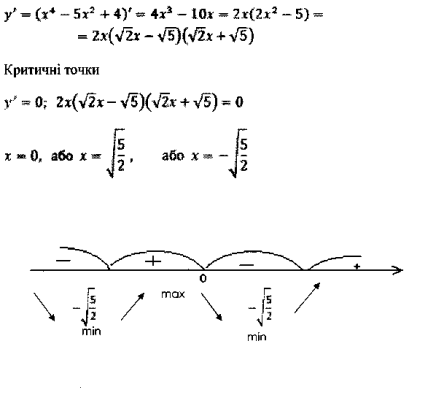
8. Визначимо проміжки опуклості заданої функції:

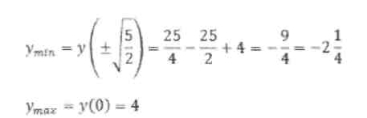
 9. За результатами дослідження будуємо графік функції.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Задачі для самостійної роботи І команда

 

1. Обчислити значення похідної функції у(х) в точці х₀ , якщо:

 

 

 

 

 

 

 

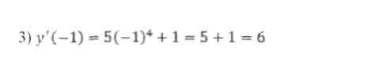
2. Записати рівняння дотичної до графіка функції в точці з абсцисою х₀

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

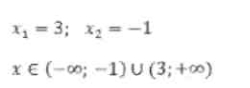
II Команда

1. Обчислити значення похідної функції у(х) в точці х₀, якщо:

2. Записати рівняння дотичної до графіка функції в точці з абсцисою х₀

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 IV. Вироблення умінь і навичок

(Конкурс «Естафета»)

Учень біля дошки розв'язує частину завдання чи все завдання, передає крейду якому- небудь члену своєї команди для продовження роботи над вправою.

І команда

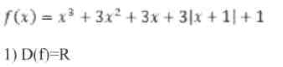1. Знайти інтервали монотонності та екстремуми

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

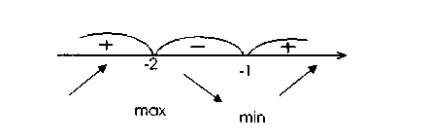
Зростає, якщо

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

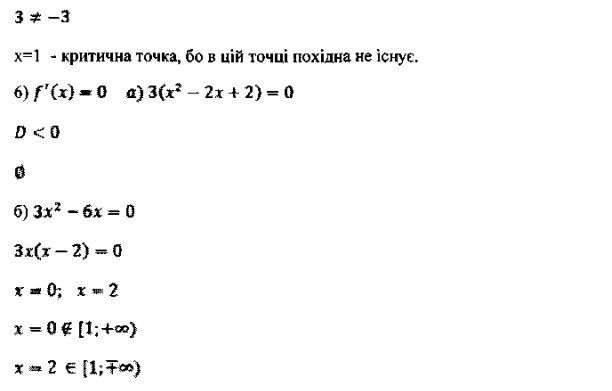
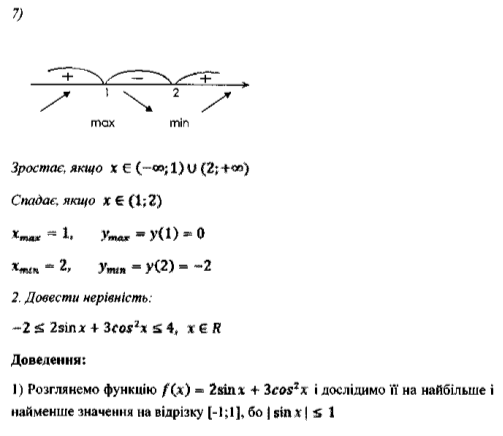
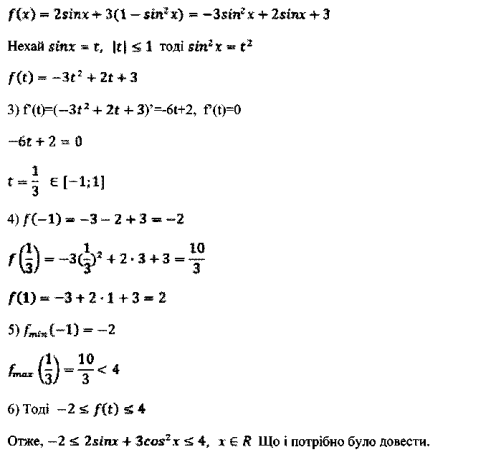
V. Конкурс капітанів Завдання для капітанів

І команда

Задача 1

Розкласти число 30 на два доданки, щоб сума їх квадратів була найменшою. Знайти добуток цих доданків.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

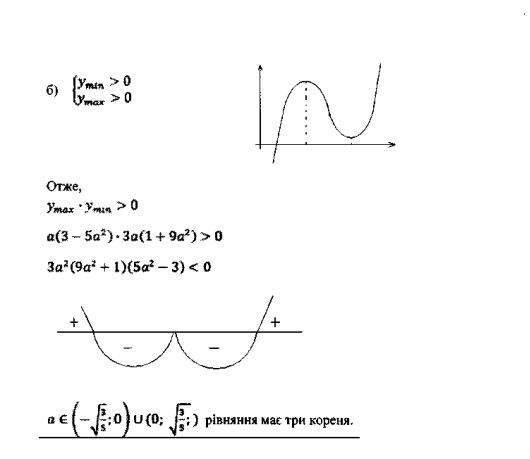
VI. Обговорення підсумків уроку та домашнього завдання

При    підготовці домашнього завдання пропонується свій «математичний маршрут», який цього разу складається з таких «ділянок»:

 

 

 

 

 

 

 

 

Запитання для самоперевірки

1.               Що називається похідною функції в точці?
2.               У чому полягає необхідна умова диференційованості функції в точці .
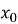3.               Які правила диференціювання функції ви знаєте?
4.               Чому дорівнює похідна складеної функції?
5.               У чому полягає геометричний зміст похідної^-?
6.               У чому полягає механічний зміст похідної?
7.               Який вигляд має рівняння дотичної до графіка функції y=f(x) в даній точці

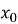
8.               Як формулюється необхідна умова екстремуму функції?
9.               Як формулюється достатня умова екстремуму функції?

10.          У чому полягає критерій сталості функції?
11.          Сформулюйте умову строгої монотонності функції на інтервалі. Як вона доводиться?
12.            Які схеми знаходження найбільшого і найменшого значення неперервної функції на відрізку ви знаєте?
13.          Як дослідити функцію на

а) монотонність;

б) екстремуми?

14. Який приклад дослідження функції ви можете навести?

Обчислити значення похідної в точці х₀, якщо:

 

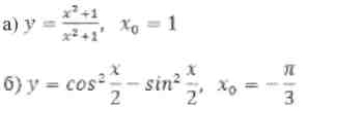
2. Записати рівняння дотичної до графіка функції в точці , якщо

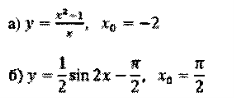
3. Знайти проміжки, на яких функція зростає (а) або спадає (б):

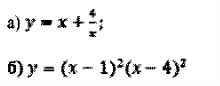
4. Знайти точки екстремуму функції:

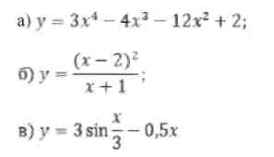
5. Дослідити і побудувати ескіз її графіка:

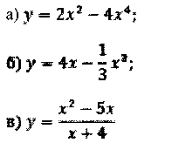
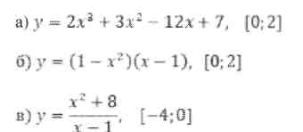
6. Знайти найбільше і найменше значення функції на даному проміжку:

 

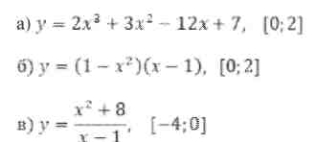
         1. Похідна суми та різниці функцій

 2. Похідна добутку функцій

    3. Похідна частки функцій

   4. Теорема Ферма

    5. Достатня ознака зростання (спадання) функції

    3. Одна грань куба лежить у площині основи правильної чотирикутної піраміди П, а вершини його протилежної грані Г - на бічних ребрах піраміди П. Одна грань куба лежить у площині грані Г, а вершини його протилежної грані - на бічних ребрах піраміди П. Ребро куба К₂ у у разів менше від ребра куба Кі . Знайти відношення об'єму куба до об'єму піраміди П. При якому значенні у це відношення найбільше?

учні мають обрати по одній задачі, однак, у разі утруднень, учні мають право самостійно проводити їх заміну в середині блоку.

VII. Рефлексивна бесіда. Дерево підсумків

1. Які  математичні  факти  було  встановлено  у розділі  «Похідна та її
застосування»?

2.                 Продовжити речення: «На уроці було найбільш цікавим і корисним...»
3.                 Мені потрібно ретельно попрацювати над...

Учні на клейких листках записують відповіді на питання і прикріплюють їх на «Дерево підсумків». За бажанням учні можуть озвучити свої думки.