Урок "Побудова графіків тригонометричних функцій"

Мета

Познайомити студентів із різними типами  прикладних задач та методами їх розв’язання за допомогою похідної; формування уміння застосовувати знання та способи дій у змінених і нових навчальних ситуаціях; поглибити знання учнів про моделювання процесів дійсності за допомогою апарата похідної;

-    розвивати пізнавальний інтерес, навички колективної праці;

-    виховувати працьовитість, зібраність, організованість, увагу, відповідальність та вимогливість до себе

Основні вимоги

     У результаті вивчення теми студенти повинні

Знати:

-         таблицю похідних;

-         формули суми, різниці, добутку, частки

-         властивості тригонометричних функцій (область визначення, область значення; парність, непарність, монотонність, періодичність; найбільше, найменше значення);

-         основні співвідношення між тригонометричними функціями одного аргументу;

-         формули  тригонометричних функцій суми та різниці двох аргументів, подвійного аргументу;

Вміти:

 - користуватися таблицею похідних;

 - обчислювати похідну суми, різниці, добутку, частки;

- перетворювати тригонометричні вирази  за допомогою формул;

- будувати   графіки  тригонометричних   функцій   і   на   них  ілюструвати властивості функцій;

- застосовувати     геометричні     перетворення     при    побудові     графіків тригонометричних функцій;

При вивчені теми слід звернути увагу на такі питання:

1.          Вірно задавати масштабну одиницю: по вісі ОY – 2  клітинки 1 одиниця,  по вісі ОХ – число π тоді 6 клітинок.
2.          При паралельному перенесенні вздовж вісі ОХ та деформації по ОХ тангенсоїди спочатку переносять асимптоти.
3.          При стискання або  розтягуванні по вісі ОY точки перетину  даного графіка з віссю ОХ залишаються без змін, а відстань по ОY збільшується (зменшується) в відповідну кількість раз. При стисканні або розтягуванні по вісі ОХ – навпаки.
4.          Під час побудови складних функцій основні перетворення можна виконувати в будь-якій послідовності. І все-таки паралельні перенесення робити останніми, оскільки стиснення і розтягування побудованих графіків зручніше робити від початку координат.

На попередньому занятті ми з’ясували, який вигляд мають графіки тригонометричних функцій. На слайді зображено чотири графіка функції. Назвати кожен з них і записати формулу.

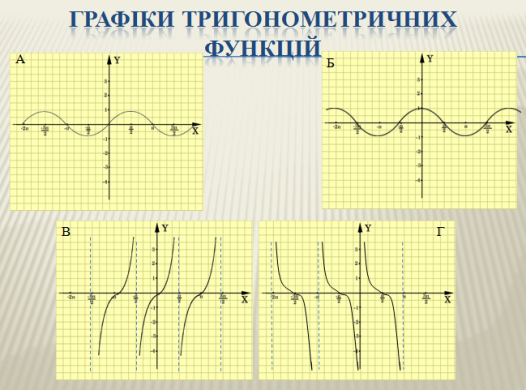
Рис. 1

Таким чином,  на минулому занятті,  ми з’ясували вигляд основних тригонометричних функцій, але на практиці, наприклад, в фізиці при вивченні гармонійних коливань, графіка напруги, необхідно вміти будувати графіки більш складних функцій.

Наприклад, щоб побудувати графік функції потрібно виконати геометричні перетворення над графіком . Отже, сьогоднішня тема нашого заняття: «Геометричні перетворення графіків функцій». Для початку згадаємо основні перетворення графіків функцій.

Завдання № 1. Розглянемо графіки на слайдах, та пояснимо, які перетворення з ними відбулися.

1. ,

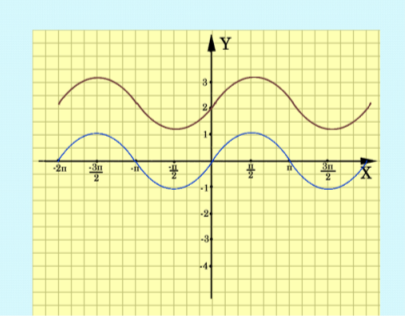
Рис. 2

2. ,    , 

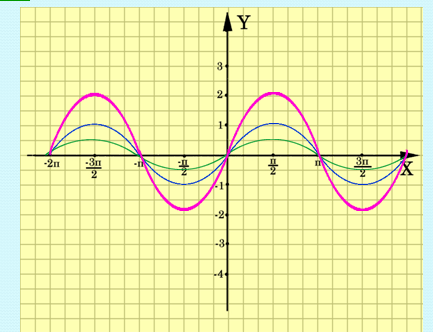
Рис. 3

3. , ,

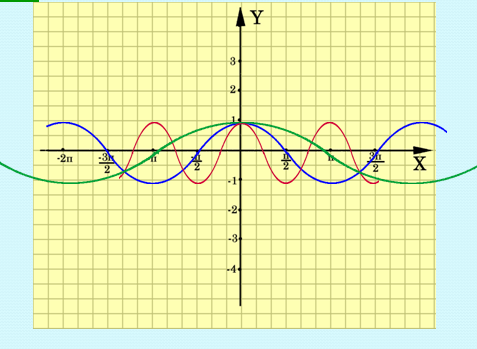
Рис. 4

4. ,

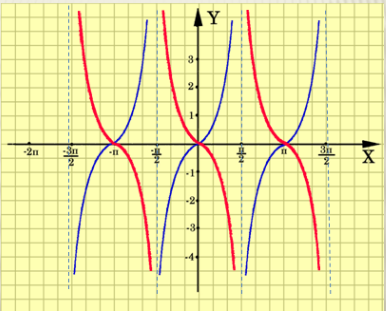
Рис. 5

Побудувати в зошитах наступні графіки функцій.

Завдання № 2. Побудувати графік функції   А)

1.              
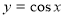
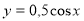2.               - стиск попереднього графіка вздовж осі ОY в 2 рази
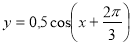3.               - паралельне перенесення другого графіка вліво на 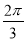одиниць (4 клітинки)
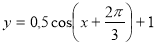4.               - паралельне перенесення останнього графіка вгору на одиницю.

Б)

1)

2) стиск  попереднього графіка вздовж осі ОХ в 3 рази

3) - паралельне перенесення другого графіка вправо на одиниць.

Завдання № 3 Проаналізуйте малюнки і назвіть геометричні  перетворення, які виконуються для побудови графіків.

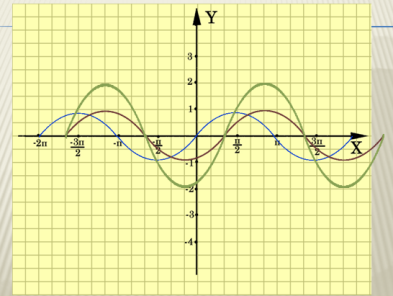
Рис. 6

1.              
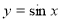
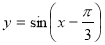2.               - паралельне перенесення графіка вправо на 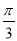одиниць;
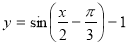3.               - паралельне перенесення останнього графіка вниз на одну одиницю.

Завдання  № 4 Серед графіків, які зображено на рисунках 1 -  4 назвіть графіки нижче поданих  функцій:

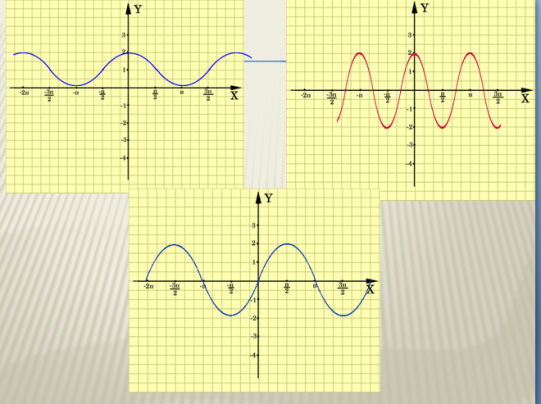
Рис. 7

Завдання № 4  Індивідуальні завдання на картках (додаток 2)

Домашнє завдання: Побудувати графіки (додаток 3)

Додаток 1

Математичний диктант

1.          Яка функція називається непарною, навести приклади.
2.          Яка область значень функції тангенса?
3.          Що таке радіан? Значення кутів одиничного кола у радіанах.
4.          Яка область значень функції синуса?
5.          Що називається графіком функції?
6.          Яка функція називається періодичною?
7.          Перевести у градусну міру .
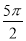8.          Яке число є найменшим додатнім періодом функції синуса та косинуса?
9.          Дайте визначення косинуса гострого кута.
10.     Знайдіть період функцій .
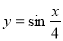11.     Знайдіть період функції  .
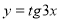12.     Перевести у радіани
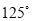
13.     Якою властивістю володіє графік парної функції?
14.     Що можна сказати про парність, непарність тригонометричних функцій.
15.     Яка область визначення функції котангенса?

Додаток 2

Додаток 3