Похідна ( урок брейн – ринг )

 

Похідна

( урок брейн – ринг )

 

Мета уроку. Формувати навички і вміння знаходити похідні

                     функцій. Ознайомити учнів з історичним

                     матеріалом, зв’язаним з поняттям «похідна».

                     Стимулювати пізнавальну діяльність учнів,

                     сприяти формуванню і розвитку системних

                     знань, колективних і між особистих відносин,

                     самостійності у виборі засобів, форм і методів

                     роботи.

Тип уроку. Урок формування вмінь та навичок.

 

Хід уроку.

 

I. Мотивація навчальної діяльності учнів, повідомлення

   теми, мети і задач уроку.

 

   Пряме не може бути кривим, а криве прямим. І все ж диференціальне числення, всупереч усім протестам людського розуму, прирівнює, за певних умов, пряме і криве одне до одного і досягає цим таких успіхів, яких ніколи не досягнути здоровому людському розумові.

   Тема сьогоднішнього уроку «Похідна» і він має назву «урок брейн – ринг». На уроці будуть змагатися  дві команди. В кінці уроку ми визначимо переможця і кращого гравця.

    В якості побажання, я хотіла б прочитати для вас наступні рядки:

   Если ты в жизни, хотя б на мгновенье   

   Истину в серце своем ощутил,

   Если луч правды сквозь мрак и сомненье

   Ярким сияньем твой путь озарил:

   Чтобы в решении своем неизменном

   Рок не назначил тебе впереди –

   Память об этом мгновении священном

   Вечно храни, как святиню в груди,

   Тучи соберутся громадой нестройной,

   Небо покроется черною мглой,

   С ясной решимостью, с верой спокойной

   Бурю ты встреть и померься с грозой!

 

   Розпочинаємо гру.

 

   ІІ. Актуалізація опорних знань учнів.

 

   Запитання 1. Що означає термін «диференціювання функцій»?

 

   В 60 – 70–і роки ХVІІ століття сталося найвидатніше відкриття усіх часів – створення нової математичної теорії: диференціальне і інтегральне числення.

   «Без інтегрального і диференціального числення математика, як наука, не могла б досягти сучасного свого розвитку.» (Х. Гюйгенс)

   «Немає жодного відкриття, що сприяло б у математиці такий щасливий і швидкий переворот, який був зроблений аналізом нескінченно малих.» (Л. Арно)

 

   Запитання 2.  Хто і в якому році ввів термін «похідна» та її позначення?

 

   В XVII столітті відбулися великі революційні зміни в математиці. За довгий час своєї кропіткої роботи ряд вчених з різних країн світу , таких як П. Ферма (1601 – 1665),         Р. Декарт (1596 – 1650), І. Ньютон (1542 – 1727),

В. Лейбніц (1646 – 1716) внесли свій внесок в створення нового потужного апарату досліджень – інтегрального та диференціального числення.

   В 1791 році Жозеф Луї Лагранж ввів позначення похідної.

 

   Запитання 3.  Означення похідної.

   Запитання 4.  Геометричний зміст похідної.

   Запитання 5.  Механічний зміст похідної.

   Запитання 6.  Похідна суми (різниці).

   Запитання 7.  Похідна добутку.

   Запитання 8.  Похідна частки.

   Запитання 9.  Похідна складеної функції.

   Запитання 10.Похідна сталої.

   Запитання 11.Похідна степеневої функції.

   Запитання 12.Похідна показникової функції.

   Запитання 13.Похідна логарифмічної функції.

   Запитання 14.Похідна синуса.

   Запитання 15.Похідна косинуса.

   Запитання 16.Похідна тангенса.

   Запитання 17.Похідна котангенса.

   Запитання 18.Рівняння дотичної.

 

ІІІ. Застосування учнями знань.

 

Перейдемо до практики.

 

Математичний диктант. Обчислити похідні функцій:

 

1. у = х² + 3х ;
2. у = sin2x + cosx ;
3. у = tg2x ;
4. у = сtg²x ;
5. у = cos(3x – 7) + sin π/2 ;

   6. у = e^x ;

   7. у = log₅x² ;

   8. у = 3^2х ;

   9. у = lnx ;

  10.у =   х ;

  11.у = ³ х².

 

  Запитання 19.Заповнити пусті клітинки таблиці.

 

7х3 – 5х	21х2 - 5	42х
cosx	-sinx
xsinx

 

 

 

 

 Запитання 20.Встановити правильний порядок обчислення 

                         похідної.

 

(sin²(2x + 3) + sin)΄ ;   cos(2x + 3)·2 ;   2sin(2x + 3) ;

2sin(2(2x + 3)) ;  2sin(4x + 6) .

 

  Запитання 21.Виправити помилки.

 

f(x) = 3x2 – 5	f ΄(1/6)	231
f(x) = 7x4 – 2x2 – x	f ΄(2)	-3
f(x) = cos3x	f ΄(π/6)	1
f (x) = 2sinx	f ΄(π/3)	1

 

Запитання 22.Потрапити із одного палацу в інший, обчисливши

                        похідні функцій, що зустрінуться на шляху.

 

 

 

 

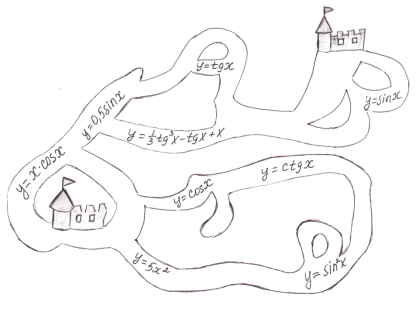
    Запитання 23.Знайти похідну функції  y = (3x²-x+7):(2x+5)  в 

                         точці  х = 1.

 

 Запитання 24.Знайти швидкість і прискорення матеріальної 

                          точки в момент часу t₀ = 4 с, якщо  х(t) = 2t² + t - 4

                             (одиниці вимірювання відстані – метри).

 

 Запитання 25.Записати рівняння дотичної до графіка функції

                          y =   в точці  х₀ = 2.

 

  ІV.  Підсумки уроку і домашнє завдання.

 

  Резерв. Історична довідка (І. Ньютон, Г.В. Лейбніц, Ж.П. Лагранж)