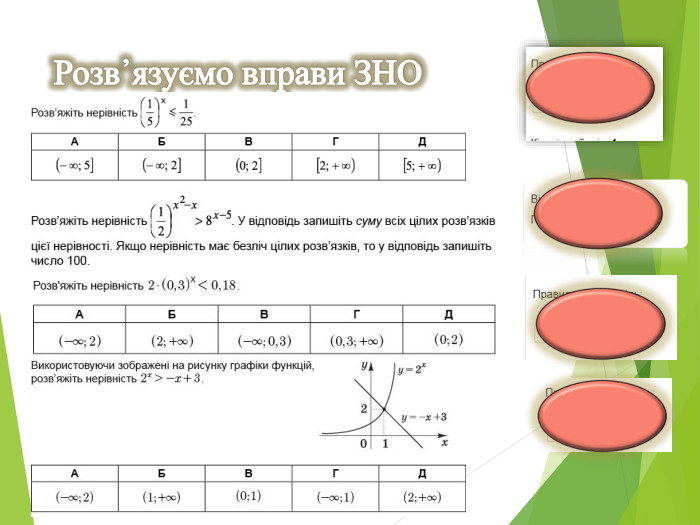
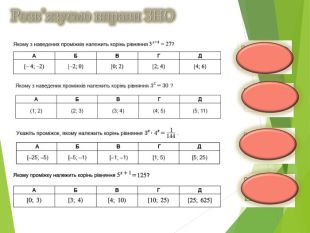
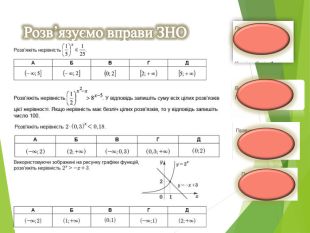
Показникові рівняння та нерівності. Основні види та способи їх розв'язування.
Про матеріал
1) зведення до однієї основи;
2)зведення до спільного показника;
3) винесення спільного множника за дужки;
4) ділення обох частин на степінь;
5) зведення до квадратного шляхом заміни;
6) розв᾽язування однорідних рівнянь.
7) функціонально - графічний метод.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку