ПОКРИТТЯ ПЛОЩИН ПРАВИЛЬНИМИ БАГАТОКУТНИКАМИ
ЗМІСТ
1.3.Аналіз одержаних результатів в перші частині
Мета: відшукати і дослідити способи покриття площин правильними багатокутниками та вказати на малюнках такі покриття.
Завданням цієї роботи.
Обґрунтувати спосіб покриття площин правильними багатокутниками Дослідити можливі випадки такої побудови. На першому етапі роботи досліджено розміщення в одній точці чотирьох правильних багатокутників.
На другом етапі досліджено існування всіх можливих випадків покриття площини правильними багатокутниками.
Методика дослідження опирається на математичне обґрунтування можливості існування покриття площини правильними багатокутниками так що, сума градусних мір всіх кутів у кожній вершині дорівнює 360º.
Такий підхід дає можливість з’ясувати існування всіх можливих варіантів покриття площини та показати на малюнках варіанти таких розміщень.
Актуальність роботи:
Нерідко результати математичних досліджень знаходять своє пряме застосування в різних галузях, зокрема в будівництві. Покриття площин у будівництві має важливе значення як для економії матеріалів, часу виконання робіт так і для створення належного психологічного комфорту у просторі де перебуває людина. На психологічний комфорт впливають не тільки правильно підібрані кольори, а й вдало підібрані форми оздоблювальних поверхонь підлоги, стін, стелі. Найбільш привабливими формами для людського ока є правильні багатокутники. Результати цієї роботи мають прикладне значення при викладанні паркетів, лицювальної плитки, мозаїки.
Новизна роботи.
В цій роботі математично обґрунтовуються всі можливі випадки покриття площини правильними багатокутниками з рівною довжиною сторін. Почавши з найбільш вживаного способу покриття площин квадратами, де в одній точці площини сходяться чотири фігури, досліджено всі інші випадки покриття площини правильними багатокутниками.
Значення роботи.
В роботі математично обґрунтовуються всі можливі випадки поєднання правильних багатокутників з рівною довжиною сторін, для створення на площині красивих симетричних орнаментів, які можна серійно виготовляти з наперед заданим малюнком. В поєднанні з кольоровою гамою це додасть поверхням привабливого вигляду.
Робота є простою за виконанням і за складністю запропонованого способу покриття площин. Доведено існування тільки 11 різних правильних паркетів у вершинах яких сходяться правильні багатокутники. До кожного випадку подано відповідні малюнки, які демонструють правильність такого розміщення. Малюнки виконані з використанням графічного редактора Paint.
Результати роботи були повідомлені для учнів 7-9 класів під час роботи шкільного факультативу з математики.
ВСТУП
Під час гри в шахи я звернула увагу на покриття частини площини (шахова дошка) квадратами. І мене зацікавило питання про покриття площин правильними багатокутниками.
Середовище у якому перебуває людина, як правило обмежене частинами площини. Це найперше: стіни, підлога, стеля кімнат, у яких проживає і працює людина. Для створення певного мікроклімату, візуального комфорту людина намагається покривати (замощувати) ці площини різними фігурами. Це проявляється в таких способах покриття площин як, паркети – покриття підлоги, лицювання плиткою стін і підлоги, мозаїка різних частин кімнат: стелі, стін, підлоги.
Щоб простір, в якому перебуває людина, був комфортним підбирають не тільки потрібні матеріали для покриття площин, а й надають цим покриттям певної форми. Для простоти опису роботи, надалі види покриття площини будемо називати паркетами.
ЧАСТИНА 1
1.1.Правильні паркети
Звернемося до Інтернету (https:uk.wikipedia.org).[ 2]
Загально відомо що, паркети, складені з однакових правильних багатокутників, називають правильними паркетами (англ. regular tilings). Існує три правильних заміщення площини: трикутний паркет, квадратний паркет і шестикутний паркет.
Правильні паркети називають також Платоновими паркетами.
Для позначення паркету з правильних p -кутників, розташованих по q навколо кожної вершини, застосовується символ Шлефлі { p , q }. Символи Шлефлі трьох правильних мозаїк: {3,6}, {4,4} і {6,3}.
Трикутний паркет замощення площини рівними правильними трикутниками, розташованими сторона до сторонни (малюнок 1).
Трикутний паркет є двоїстим шестикутного паркету: якщо прибрати по одній стороні суміжних трикутників, то утвориться шестикутний паркет. Символ Шлефлі трикутного паркету – {3,6}, що означає, що в кожній вершині паркету сходяться 6 трикутників.
Трикутні розбиття поширені в 3D-графіці. Трикутний паркет є основою для деяких ігор на клітинному полі: моделі «Життя» та інших двовимірних клітинних автоматів, кільцевих флексагонів і т.п., але такі розбиття ігрових карт використовуються відносно рідко. Великим недоліком трикутного розбиття в іграх є великий периметр при невеликій площі (на протилежність шестикутного паркету).
Квадратний паркет (регулярний квадратний паркет) — дискретна модель замощення площини рівними квадратами, розташованими сторона до сторони так, що, вершини чотирьох суміжних квадратів знаходяться в одній точці (малюнок 2).
Існує безліч нерегулярних квадратних паркетів, в яких ряди прилеглих квадратів по одній стороні взаємно зміщені на довільне зміщення. Регулярний квадратний паркет є двоїстим самому собі: якщо з'єднати центри суміжних квадратів, то проведені відрізки знову дадуть квадратний паркет. Символ Шлефлі квадратного паркету – {4, 4}, що означає, що в кожній вершині паркету сходяться 4 чотирикутника.
Поле квадратного паркету є основою для багатьох ігор і головоломок, наприклад, поле шахівниці є квадратним паркетом, також і для багатьох інших ігор на квадратному полі: кросвордів, поліміно, моделі «Життя» та інших двовимірних клітинних автоматів.
Регулярний квадратний паркет (регулярна сітка) використовується як модель робочого поля в алгоритмах трасування друкованих плат, таких як алгоритм канального трасування.
Шестикутний паркет
Шестикутний паркет – замощення площини рівними правильними шестикутниками, розташованими сторона до сторонни (малюнок 3). Шестикутний паркет є двоїстим трикутного паркету: якщо з'єднати центри суміжних шестикутників, то проведені відрізки дадуть трикутний паркет. Символ Шлефлі шестикутного паркету – {6,3}, що означає, що в кожній вершині паркету сходяться три шестикутника.
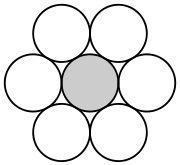
Шестикутний паркет є моделлю найбільш щільного пакування кіл на площині. Замощення площини правильними шестикутниками є основою для деяких ігор на клітинному полі: гексагональних шахів, варіантів моделі «Життя» та інших двовимірних клітинних автоматів, кільцевих флексагонів і т.п.
Існує гіпотеза, яка стверджує, що шестикутний паркет є найкращим способом розділити поверхню на ділянки рівної площі з найменшим сумарним периметром.
Структури, подібні до шестикутного паркету, існують у природі у вигляді бджолиних стільників. Графени графіту також утворюють зв'язки, подібні до граней шестикутного паркету. Штучно синтезовані трубчасті графенові листи відомі як вуглецеві нанотрубки.
Шестикутний паркет можна розглядати як модель щільного пакування кіл на площині (малюнок 4).
Все ж таки, найпростіший спосіб покриття площини правильними фігурами це – покриття її рівними квадратами. Поставимо запитання, які будуть предметом дослідження в цій роботі:
- Скільки є способів покриття площини правильними багатокутниками так, щоб до кожної вершини прилягало рівно чотири правильних багатокутники?
- Скільки існує різних правильних паркетів у вершинах яких сходяться правильні багатокутники?
1.2.Перша частина дослідження
Пошук і дослідження відповіді на запитання: «Скільки є способів покриття площини правильними багатокутниками так, щоб до кожної вершини прилягало рівно чотири правильних багатокутники?»
Найпростіший спосіб покриття площини правильними фігурами це – покриття її рівними квадратами (мал.2). Виникає природне запитання: скільки є ще таких способів покриття площини правильними многокутниками так, щоб до кожної вершини було рівно чотири правильних многокутники і у кожній вершині буде однакове розміщення правильних многокутників.
Щоб дати відповідь на це питання розглянемо одну з таких вершин. У вершині сходяться кути чотирьох правильних многокутників. З геометрії [2] ми знаємо, що сума кутів правильного n – кутника визначається за формулою:
Sn = 1800 (n – 2) , а один його кут α визначається за формулою:
.
Розглянемо найбільш загальний варіант, коли всі чотири правильні многокутники мають певну кількість вершин. Наприклад, p-кутник, q-кутник, r-кутник, s-кутник, де p, q, r, s – натуральні числа, які дорівнюють числу сторін правильного многокутника. Кожний з таких кутів, відповідно дорівнює:
, 
, 
, 
, а їх сума
Спростивши цей вираз, отримаємо:
Будемо вважати що, 
. З цього випливає що, найменше число p має таку оцінку: 
. p = 3, бо це найменш можливе число сторін у правильного многокутника ( у правильного трикутника).
, бо в іншому разі 
Отже, p = 3 або p = 4.
Розглянемо випадок коли p = 3, тоді 
або 
Оцінимо можливі значення q. 3 ≤ q < 5. Оцінка 3 ≤ q випливає з умови 3 = 
.
q < 5, бо тоді 
, ( 
.
Розглянемо q = 3. Тоді, 
або 
.
Це рівняння в натуральних числах має два розв’язки:
-
r = 4, s = 12
,
-
r = 6, s = 6
Розглянемо q = 4. Тоді, 
або 
.
Це рівняння в натуральних числах має один розв’язок:
r = 4, s = 6 
Зробимо перший висновок.
Числа p, q, r, s можуть набувати значень (таблиця 1):
Таблиця 1.
|
Число сторін правильного багатокутника № варіанта |
p |
q |
r |
s |
|
1 |
3 |
3 |
4 |
12 |
|
2 |
3 |
3 |
6 |
6 |
|
3 |
3 |
4 |
4 |
6 |
Розглянемо випадок коли p = 4, тоді 
або 
Оцінимо можливі значення q. 4 ≤ q < 5. Оцінка 4 ≤ q випливає з умови 4 = .
q < 5, бо тоді 
, ( 
.
Отже, q = 4 і тоді 
або 
Останнє рівняння має лише один розв’язок у натуральних числах r = 4, s = 4.
Зробимо другий висновок.
Числа p, q, r, s можуть набувати значень:
|
p |
q |
r |
s |
|
4 |
4 |
4 |
4 |
Об’єднаємо перший і другий висновок у один (таблиця 2):
|
Число сторін правильного багатокутника № варіанта |
p |
q |
r |
s |
|
1 |
3 |
3 |
4 |
12 |
|
2 |
3 |
3 |
6 |
6 |
|
3 |
3 |
4 |
4 |
6 |
|
4 |
4 |
4 |
4 |
4 |
1.3.Аналіз одержаних результатів в перші частині
Проаналізуємо одержані результати дослідження.
Для четвірки чисел (4, 4, 4, 4) покриття площини здійснюється рівними квадратами. У кожній вершині такого покриття сходиться чотири квадрати (малюнок 5).
Таке покриття має властивість симетричності покриття.
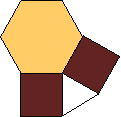
Для четвірки чисел (3, 4, 6, 4) покриття площини здійснюється правильним трикутником, двома рівними квадратами та правильним шестикутником. У кожній вершині такого покриття сходиться по чотири таких правильних многокутників (малюнок 6). Таке покриття має центр симетрії – центр правильного шестикутника, та два види осей симетрії:
- прямі, які проходять через великі діагоналі правильного шестикутника;
-
прямі, які проходять через серединні перпендикуляри до сторін правильного шестикутника.
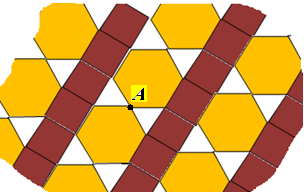
Для такого випадку можливе і інше розміщення цих фігур (малюнок 7).
Але для такого розміщення не виконується властивість симетричного розміщення покриття. Зокрема, у точці А, де сходяться два правильні шестикутники відсутні квадрати. Тому, таке покриття площини неможливе.
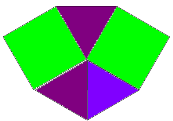
Для четвірки чисел (3, 6 , 3, 6) покриття площини здійснюється двома правильними рівними трикутниками та двома правильними рівними шестикутниками. У кожній вершині такого покриття сходиться по чотири таких правильних многокутників (малюнок 8).
Таке покриття має три види осей симетрії:
- прямі, які проходять через центри шестикутників;
- прямі, які проходять через діагоналі шестикутників;
- прямі, які проходять через середини сторін шестикутників.
Для такого випадку можливе і інше розміщення цих фігур (3, 3, 6, 6) (малюнок 9)
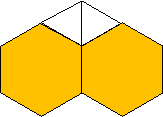
Але для такого розміщення не виконується властивість симетричного розміщення покриття. Так, у точках В і С, буде різне чергування трикутників і шестикутників. Тому, таке покриття площини неможливе.
Для четвірки чисел (3, 3, 4, 12) покриття площини здійснюється двома правильними трикутниками, квадратом та правильним дванадцятикутником. У кожній вершині такого покриття сходиться по чотири правильних многокутників.
Можливі два розміщення таких правильних многокутників (малюнки 10, 11). Але для таких розміщень не виконується властивість симетричного розміщення покриття. Зокрема, в білій і синій зонах порушується правило розміщення тільки чотирьох правильних багатокутників. Тому, покриття площини двома правильними трикутниками, квадратом і правильним дванадцятикутником неможливе.
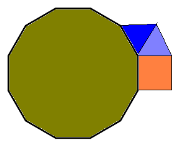
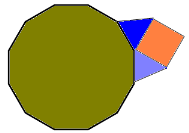
Висновки до першої частини
В результаті дослідження знайдено відповідь на запитання: « Скільки є способів покриття площини правильними багатокутниками так, щоб до кожної вершини прилягало рівно чотири правильних багатокутники?»
Існує тільки три правильних покриття, у яких до кожної вершини підходить чотири правильних багатокутники.
|
p-кутник |
q-кутник |
r-кутник |
s-кутник |
|
3 |
6 |
3 |
6 |
|
3 |
4 |
4 |
6 |
|
4 |
4 |
4 |
4 |
Знайдено четвертий варіант покриття площини чотирма правильними багатокутниками, які прилягають до однієї вершини (3, 3, 4, 12): два правильних трикутники, один квадрат і правильний дванадцятикутник. Але таке покриття площини містить точки у яких більше як чотири правильних багатокутники. Тому цей варіант не є розв’язком поставленого питання.
У другій частині роботи буде пошук і дослідження відповіді на запитання:
Скільки існує різних правильних паркетів у вершинах яких сходяться правильні багатокутники?
ЧАСТИНА 2
2.1. Пошук і дослідження відповіді на запитання: «Скільки існує різних правильних паркетів у вершинах яких сходяться правильні багатокутники?»
Для розв’язання цієї задачі дослідимо вершини правильного паркету. Назвемо вершину утворену сторонами правильних багатокутників, які в ній сходяться, зіркою паркету. Так для покриття площини квадратами, зірка матиме такий вигляд . Позначимо,
mi – число правильних багатокутників, які утворюють зірку. mi N.
αn – градусну міру внутрішнього кута відповідного правильного багатокутника (n-кутника ). n – число сторін (внутрішніх кутів) правильного багатокутника.
Тоді, в кожній зірці паркету виконується рівність:
m1α1 + m2α2 + m3α3 + … + mnαn = 360º. (2.1)
З геометрії [2] ми знаємо, що сума кутів правильного n-кутника визначається за формулою:
Sn = 1800 (n – 2), а його внутрішній кут α дорівнює: 
.
Тоді рівність (2.1) набуває вигляду:
m1
+ m2
+ m3
+ … + mn
= 360º. (2.2)
m1, m2, m3, … , mn – кількість правильних багатокутників.
n1, n2, n3, … , nn – число сторін відповідних правильних багатокутників.
Поділимо ліву і праву частину рівності (2.2) на 180º одержимо
m1
+ m2
+ m3
+ … + mn
= 2. (2.3)
Або, m1
)+ m2
) + m3
) + … + mn
= 2. (2.4)
Отримали рівняння, коренями якого є натуральні числа m1 , m2 , m3 ,…, mn.
З геометрії [2] ми знаємо, що внутрішній кут правильних багатокутників менший 180º і має відповідні значення подані в таблиці 3:
Таблиця 3.
|
Число сторін правильного багатокутника |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Градусна міра внутрішнього кута |
600 |
900 |
1080 |
1200 |
|
1350 |
1400 |
1440 |
|
1500 |
Якщо зірку будуть утворювати тільки два правильних багатокутники, то один з них має бути більшим 180º, що неможливо, отже найменша кількість правильних багатокутників, які утворюють зірку дорівнює три.
Якщо зірку будуть утворювати сім правильних багатокутників,то
7600 > 3600, що неможливо, отже найбільша кількість правильних багатокутників, які утворюють зірку дорівнює шість, бо ще можливо
6600 = 3600 .
Висновок, розв’язування поставленої задачі зводиться до аналізу таких можливих варіантів, коли зірку утворюють 3, 4, 5 або 6 правильних багатокутників.
Випадок, коли зірку утворюють чотири правильних багатокутники розглянуто в першій частині.
Розглянемо випадок, коли зірку утворюють три правильних багатокутники. При цьому можливі такі комбінації з трьох багатокутників:
- три однакові багатокутники;
- два багатокутники однакові і один інший;
- всі три багатокутники різні.
Для першого випадку рівняння (2.4) набуває вигляду
3
= 2. (2.5)
Звідси, n = 6, тобто у кожну зірку утворює три однакових 6 – кутники. За символом Шлефлі трикутного паркету – {6,3 }, або (6, 6, 6).
Для другого випадку рівняння (2.4) набуває вигляду
= 2. (2.6)
|
n |
3 |
4 |
6 |
10 |
|
k |
12 |
8 |
6 |
5 |
Виразимо k через n. k = 
. Звідси випливає, при n > 10, k – дробове. Складемо таблицю можливих цілих значень k:
Випадок n = k = 6 дає вже отриманий раніше результат {6,3 } – зірку утворюють три правильних 6-кутники. Запишемо три інші розв’язки:
α3 + 2α12 = 60º + 2150º = 360º - один правильний трикутник і два правильні дванадцятикутники (малюнок 12). За символом Шлефлі (3, 12, 12).
α4 + 2α8 = 90º + 2135º = 360º - один правильний чотирикутник і два правильні восьмикутники (малюнок 13). За символом Шлефлі (4, 8, 8).
α10 + 2α5 = 144º + 2108º = 360º - один правильний десятикутник і два правильні п’ятикутники (малюнок 14). За символом Шлефлі (10, 5,5).
При побудові правильного паркету типу 
(малюнок 14), з’ясувалося, що утворюється кут β = 360º – 3108º = 36 º. Це порушує принцип симетрії. Отже, правильного паркету типу не існує.
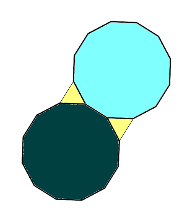
Малюнок 12.
Малюнок 13.
Малюнок 14.
Для третього випадку рівняння (2.4) набуває вигляду
= 2.
Або, 
(2.7)
Перед тим, як шукати розв’язки рівняння (2.7), звернемо увагу на можливе розміщення правильних багатокутників одних відносно інших.
Твердження. Число сторін кожного правильного багатокутника має бути парним.
Справді, якщо один із трьох правильних багатокутників матиме непарну кількість сторін, тоді два інших розміщуються навколо нього по черзі (малюнок 15). Станеться так, що обійшовши навколо правильного багатокутника з непарною кількістю сторін, одержимо поруч два однакових багатокутники.
Малюнок 15.
Врахувавши це твердження n = 2n1, m = 2m1, k = 2k1 і рівняння (2.7) набуває вигляду 
(2.8)
Так як n1, m1, k1 – різні, нехай n1 < m1 < k1 .
Якщо n1 = 2, m1 = 3, то k1 = 6, бо 
Отже, n = 4, m = 6, k = 12. Або, α4 + α6 + a12 = 90º + 120º + 150º = 360º - один квадрат, один правильний шестикутник і один правильний дванадцятикутник (малюнок 16). За символом Шлефлі (4, 6, 12).
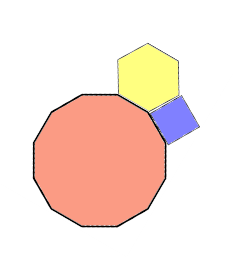
Малюнок 16.
Найменше число n не може бути більшим 6, бо тоді 
= 
Отже інших розв’язків, крім (4, 6, 12), рівняння (2.7) немає.
Висновок 2.1. Для випадку коли зірку утворюють три правильних багатокутники цими багатокутниками є:
(6, 6, 6), (3, 12, 12), (4, 8, 8), (4, 6, 12).
Розглянемо випадок, коли зірку утворюють п’ять правильних багатокутників. Треба знайти цілі розв’язки рівняння (2.4), яке набуває вигляду
= 2.
Або, 
(2.9)
Приймемо 3 ≤ n ≤ m ≤ k ≤ p ≤ q. Тоді n = m = k = 3, бо в іншому випадку 
Тоді, 
Останнє рівняння має тільки такі цілі розв’язки: (4; 4) і (3; 6). А рівняння (2.9) має такі цілі розв’язки: (3, 3, 3, 3, 6) – чотири правильних трикутники і один правильний шестикутник (малюнок 17).
Малюнок 17.
(3, 3, 3, 4, 4) – три правильних трикутники і два квадрати (малюнок 18).
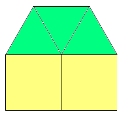
Малюнок 18.
Цікавим є випадок розміщення (3, 3, 4, 3, 4) (малюнок 19).
Малюнок 19.
Висновок 2.2. Для випадку коли зірку утворюють п’ять правильних багатокутників цими багатокутниками є:
(3, 3, 3, 3, 6), (3, 3, 3, 4, 4) або (3, 3, 4, 3, 4).
Розглянемо випадок, коли зірку утворюють шість правильних багатокутників. Треба знайти цілі розв’язки рівняння (2.4), яке набуває вигляду
= 2.
Або, 
Врахувавши умову 3 ≤ n ≤ m ≤ k ≤ p ≤ q ≤ r один єдиний результат:
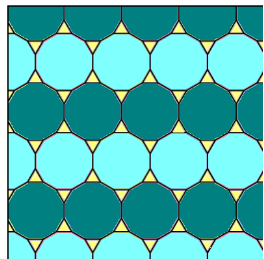
Висновок 2.3. Для випадку коли зірку утворюють шість правильних багатокутників цими багатокутниками є: (3, 3, 3, 3, 3, 3) – шість правильних трикутників (малюнок 20).
Малюнок 20.
Підсумок проведеної роботи.
Підведемо підсумок другої частини, а отже і всієї роботи.
- Відповіді на запитання: «Скільки існує різних правильних паркетів у вершинах яких сходяться правильні багатокутники?» можна подати у вигляді таблиці 4.
Таблиця 4.
|
Кількість видів правильних паркетів |
Кількість правильних багатокутників у одній вершині (утворюють зірку) |
Вид розміщення правильних n-кутників у одній вершині |
|
|
3 |
(6, 6, 6) |
|
|
3 |
(3, 12, 12) |
|
|
3 |
(4, 8, 8) |
|
|
3 |
(4, 6, 12) |
|
|
4 |
(3, 6, 3 , 6) |
|
|
4 |
(3, 4, 4, 6) |
|
|
4 |
(4, 4, 4, 4) |
|
|
5 |
(3, 3, 3, 3, 6) |
|
|
5 |
(3, 3, 3, 4, 4) |
|
|
5 |
(3, 3, 4, 3, 4) |
|
|
6 |
(3, 3, 3, 3, 3, 3) |
- Всього існує 11 різних правильних паркетів у вершинах яких сходяться правильні багатокутники.
- Під час розв’язування рівнянь, знайдено два способи покриття площини правильними багатокутниками, які покривають не всю площину: (10, 5, 5), (3, 3, 4, 12), а отже, не є розв’язками поставленої задачі.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1.Геометрія: підручник для 9 класу загальноосвітніх навчальних закладів./ О.С.Істер. – Київ: Генеза, 2017. – 240 с.
2.ІНТЕРНЕТ-РЕСУРСИ https:uk.wikipedia.org.
1
про публікацію авторської розробки
Додати розробку