Поняття площі многокутника. Площа прямокутника
Тема. Поняття площі многокутника. Площа прямокутника
Мета: сформувати в учнів уявлення про площу многокутника, одиницю вимірювання площ, властивості (аксіоми) площ, рівновеликі фігури, рівноскладені многокутники, властивість рівноскладених многокутників та оберненого твердження; працювати над засвоєнням учнями ідеї доведення теореми про площі прямокутника та квадрата. Формувати вміння застосовувати теореми для обчислення площ прямокутника і квадрата.
Тип уроку: засвоєння нових знань.
Наочність та обладнання: конспект «Плота. Властивості площ. Площа прямокутника».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Засвоєння учнями матеріалу попередніх уроків перевіряється під час виконання комплексної самостійної роботи, складеної за змістом таких матеріалів:
1) Зошит для підсумкового та тематичного оцінювання. Геометрія, 8 клас (ЄршоваА. П., Голобородько В. В.); тест, варіант 1, 2; тема 4, с. 25, 27, завдання 3 і 7;
2) Зошит для самостійних і контрольних робіт. Геометрія, 8 клас (ЄршоваА. П., Голобородько В. В.); блок 7, с. р. 20, варіанти 1-4, завдання 1, 2;
3) Зошит для самостійних і контрольних робіт. Геометрія, 8 клас; блок 7, с. р. 21, варіанти 1 – 4, завдання 1.
Правильність виконання письмових завдань домашньої роботи вчитель перевіряє, зібравши зошити учнів на перевірку.
Варіант 1
- Сума кутів опуклого п-кутника дорівнює:
а) 180°п – 180°; б) 180°п – 2; в) 360°; г) 180°(п – 2).
-
Знайдіть зовнішній кут опуклого п'ятикутника, всі внутрішні кути
якого рівні.
а) 144°; б) 108°; в) 72°; г) 36°.
- Скільки діагоналей виходить з однієї вершини дев'ятикутника?
- Чи існує чотирикутник з найменшим кутом 91°?
- Скільки діагоналей має шестикутник?
- Скільки сторін має многокутник, якщо сума його зовнішніх кутів дорівнює сумі внутрішніх?
- Знайдіть суму кутів опуклого дев'ятикутника.
- Визначте кількість сторін опуклого многокутника, сума кутів якого дорівнює 2 520°.
Варіант 2
-
Сума зовнішніх кутів опуклого п -кутника, взятих по одному при
кожній вершині, дорівнює:
а) 180°п – 180°; б) 180°п – 2; в) 360°; г) 180°(п – 2).
- Знайдіть внутрішній кут опуклого шестикутника, всі зовнішні і кути якого рівні.
а) 60°; б) 120°; в) 150°; г) 180°.
- Скільки діагоналей виходить з однієї вершини п'ятнадцяти-кутника?
- Чи існує чотирикутник з найбільшим кутом 89°?
- Скільки діагоналей має семикутник?
- Скільки сторін має многокутник, якщо всі його зовнішні кути прямі?
- Знайдіть суму кутів опуклого семикутника.
- Визначте кількість сторін опуклою многокутника, сума кутів якого дорівнює 2 340°.
III. Формулювання мети і завдань уроку
Учитель нагадує учням про стратегічну мету вивчення розділу, яка була намічена раніше (див. урок 42): узагальнити відомості про многокутники та геометричні величини, пов'язані з поняттям многокутника. Узагальнити відомості, які здобули учні в початкових класах та з життєвого досвіду, про зміст та властивості поняття «площа», а також довести справедливість відомої з початкових класів формули площі прямокутника — не і є головна мета уроку.
VI. Актуалізація опорних знань
Для успішного засвоєння учнями змісту понять уроку та можливості вільно їх використовувати під час розв'язування змістових задач учням слід активізувати знання і вміння щодо одиниць вимірювання площ; ознак рівності трикутників; властивостей паралелограмів; означення і властивостей прямокутника і квадрата та формул периметрів цих чотирикутників.
Виконання усних вправ
- На підлозі розстелені два килими: один площею 6 м2, другий — 8 м2. Килими частково накладені один на одного — по фігурі, площа якої дорівнює 1 м2. Яку площу підлоги закривають килими?
- Під час вимірювання площ земельних ділянок використовують різні одиниці вимірювання. Що означає гектар; ар?
- Що означає «сотка» городу?
- Чи одне й те саме означають ар і сотка?
- ABCD — паралелограм (рис. 1). Доведіть, що ОМ = ОК .
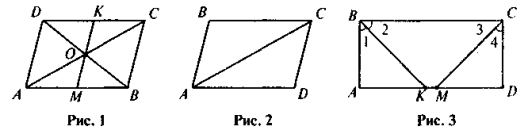
- ABCD — паралелограм (рис. 2). Доведіть, що ΔABC = ΔCDA.
-
ABCD — прямокутник,
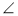 1 =
1 =  2,
2,  3 =
3 = 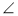 4 (рис. 3). Доведіть, що
4 (рис. 3). Доведіть, що
ВК = СМ.
- Чи правильні твердження?
1) Кожний квадрат є прямокутником.
2) Існує ромб, який є прямокутником.
3) Жодний прямокутник не є ромбом.
4) Існує квадрат, який не є ромбом.
V. Засвоєння знань
План вивчення нового матеріалу
- Зміст поняття «площа многокутника».
- Одиниці вимірювання площ.
- Спосіб наближеного обчислення площ.
- Аксіоми площ.
- Рівновеликі фігури. Рівноскладені многокутники. Властивість рів-носкладених многокутників.
- Теорема про площу прямокутника. Площа квадрата.
Матеріал, який винесено для засвоєння на урок, традиційно вивчався в темі «Площі» перед вивченням формул площ окремих многокутників. У цьому матеріалі зібрані всі відомості про загальний зміст та властивості поняття «площа многокутника», які учні здобули під час вивчення математики в школі впродовж попередніх років навчання. Деякі з цих властивостей учні сприймали та використовували на інтуїтивному рівні, інші з них — формулювались у вигляді тверджень під час вивчення теми «Площі» у 5 класі. На цьому уроці всі ці відомості повторюються, узагальнюються та систематизуються відповідно до загальної логіки вивчення геометричних понять (див. Геометрія в таблицях, Є. П. Нелін, таблиця І). Слід відзначити, що попри традиційний зміст, матеріал уроку, поданий у підручнику (п.16.1), має більш високий науковий рівень (вводиться поняття аксіоми площ, а зміст поняття площа многокутника, формулюється як «...додатна величина, числове значення якої задовольняє аксіоми площ»). Також цей матеріал (порівняно з відповідним матеріалом традиційного підручника) доповнено поняттями рівновеликих многокутників та рівноскладених многокутників, а також властивостями цих понять для многокутників (без доведення). Це сприяє, по-перше, підвищенню рівня математичної культури учнів, по-друге, збагачує арсенат засобів для розв'язування задач на застосування поняття площі многокутника, в тому числі для аргументації доведення формул площ паралелограма, трикутника, трапеції. Підсумком вивчення матеріалу є вивчення теореми про площу прямокутника, а також її наслідку (площа квадрата). Зауважимо, що формулювання теореми в підручнику дещо відрізняється від традиційного (поняття висоти й основи прямокутника не використовуються, замість них використовуються поняття сусідніх сторін прямокутника. Під час вивчення цього питання за новим підручником учні знайомляться лише з частиною традиційного доведення (розглядається лише випадок, коли сторони прямокутника а і b виражаються додатними раціональними числами, тобто можуть бути розбиті на натуральне число деяких одиничних відрізків). Повне доведення теореми пропонується для вивчення додатково (для сильних учнів). Формула площі квадрата виводиться як наслідок із формули площі прямокутника.
Для того щоб правильно розставити акценти, під час викладення матеріалу вчителю слід дотримуватися змісту підручника.
|
Конспект 17 |
|
|
Площа. Властивості площ. Площа прямокутника |
|
|
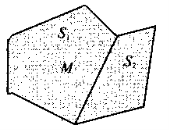
Для площі S многокутника М справедливо, що: 1) S > 0. 2) Якщо M розбити на частини з площами S1 і S2, то S = S1 + S2. 3) Одиниця вимірювання площі в одиничних квадратах: 1 мм2 1 см2 і т. д. |
|
|
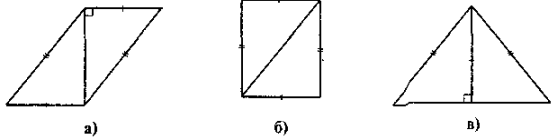
4) Якщо M1 = М2, то S1 = S2. 5) Якщо S1 = S2, то M1, і M2 — рівновеликі. 6) Нарис, а, б, в фігури є рівноскладеними. |
|
|
|
|
|
Многокутники, складені з однакової кількості відповідно рівних многокутників, називаються рівноскладеними. 7) Якщо M1, М2 — рівноскладені. то S1 = S2. |
|
|
Площа прямокутника |
|
|
|
|
|
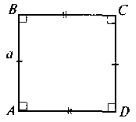
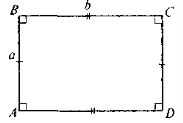
Для ABCD — прямокутника АВ = а , ВС = b S = ab. Для ABCD — квадрата (АВ = а) S = a2 |
|
З метою закріплення термінології (рівновеликі фігури, рівноскладені многокутники, властивість рівновеликих многокутників) та формул площ прямокутника і квадрата учні мають розв'язати усні вправи.
Виконання усних вправ
- Площі двох многокутників рівні. Чи означає це, що самі многокутники також рівні?
- Два прямокутники мають рівні периметри. Чи є вони рівновеликими?
- Через середини двох протилежних сторін паралелограма проведено пряму. В якому відношенні вона ділить площу паралелограма?
- Визначте, які з наведених тверджень правильні:
а) якщо діагоналі двох квадратів рівні, то ці квадрати рівновеликі;
б) два рівновеликі прямокутники рівні;
в) два рівновеликі квадрати рівні.
- Сторона квадрата дорівнює меншій стороні прямокутника. Яка з цих фігур має більшу площу?
- У трикутнику ABC проведено середні лінії. Вони поділили трикутник на 4 частини. Площа однієї з частин дорівнює 10. Чому дорівнюють площі інших частин?
- Як розрізати на частини два рівних маленьких квадрати, щоб із цих частин можна було скласти один великий квадрат?
- Визначте площу квадрата, описаного навколо кола, радіус якого R.
- Квадрат і прямокутник мають рівні площі. Сторона квадрата дорівнює 12, а одна зі сторін прямокутника — 9. Чому дорівнює друга сторона прямокутника?
- Периметр квадрата дорівнює 32. Чому дорівнює площа цього квадрата?
Виконання письмових вправ
- Знайдіть площу прямокутника ABCD, якщо.
а) АВ = 9 см, ВС = 4 см;
б) АВ : ВС = 5 : 1, PABCD = 48 см;
в) AD = 12 см, АС = 13см.
-
Діагональ квадрата дорівнює 12
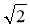 м. Знайдіть площу квадрата.
м. Знайдіть площу квадрата.
- Площа прямокутника дорівнює 128 см2. Знайдіть сторони прямокутника, якщо одна з них удвічі більша за іншу.
- Бісектриса кута прямокутника ділить його сторону на відрізки завдовжки 3 см і 4 см. Знайдіть площу прямокутника. Скільки розв'язків має задача?
Розв'язування як усних, так і письмових завдань уроку передбачає вільне володіння учнями ознаками рівності трикутників, властивостей прямокутника, вираження сторони квадрата через його діагональ (v цьому сенсі слід звернути увагу на результат письмової задачі 2: 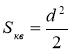 , цю формулу слід зафіксувати в зошитах учнів). Для того щоб встигнути розв'язати всі заплановані задачі, розв'язання письмових задач не треба записувати в зошити повністю; достатньо виконати прикидку розв'язання на чернетках із наступним обговоренням розв'язання.
, цю формулу слід зафіксувати в зошитах учнів). Для того щоб встигнути розв'язати всі заплановані задачі, розв'язання письмових задач не треба записувати в зошити повністю; достатньо виконати прикидку розв'язання на чернетках із наступним обговоренням розв'язання.
VII. Підсумки уроку
Для фігур, зображених нарис. 4, доберіть відповідне поняття: рівні, рівновеликі, рівноскладені. Поясніть свій вибір.
a) ABCD — прямокутник б) MNKP — квадрат

VIII. Домашнє завдання
Вивчити зміст понять, що розглядалися на уроці.
Розв'язати задачі.
- Сторони прямокутника дорівнюють 9 см і 25 см. Знайдіть периметр квадрата, рівновеликого даному прямокутнику.
- Площа квадрата дорівнює 32 см2. Знайдіть його периметр.


про публікацію авторської розробки
Додати розробку