Розробка уроку на тему "Площа трапеції"

Тема. Площа трапеції

Мета: закріпити знання учнями формул для обчислення площі три­кутника. Розглянути формулу для обчислення площі трапеції. Форму­вати в учнів уміння та навички застосовувати цю формулу для обчис­лення площі трапеції.

Тип уроку: засвоєння вмінь та навичок.

Наочність та обладнання: конспект «Площа трикутника. Площа трапеції».

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

Як і на кількох попередніх уроках, щоб зекономити час, на цьому етапі уроку учні коментують розв'язання домашніх задач за готовими рисунками, виконаними на дошці заздалегідь (або самим учителем, або учнями).

Засвоєння змісту теоретичного матеріалу та його розуміння перевіряється під час самостійного виконання учнями тестових завдань (див. Зошит для підсумкового та тематичного оцінювання).

Тестове завдання

Варіант І

1. Назвіть формулу площі прямокутника зі сторонами а і b .

а) ; б) ; в) а² + b²; г) ab.

2. Знайдіть площу ромба ABCD, якщо АС = 5 см, BD = 8 см.
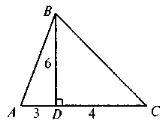
   а) 20 см²; б) 40 см²; в) 10 см²; г) 13 см².
3. За даними рисунка знайдіть площу три­кутника ABC.

а) 42;   б) 84;  в) 13;  г) 21.

4. Знайдіть площу прямокутника зі сторо­ною 5 м і діагоналлю 13 м.
   а) 60 см²; б) 60 м²; в) 65 м²; г) 156 м².
5. Дві сторони трикутника дорівнюють 8 см і 12 см, а висота, прове­дена до меншої з них, — 3 см. Знайдіть висоту, проведену до біль­шої сторони.

а) 4 см; б) 2 см; в) 4.5 см; г) 10 см.

6. Знайдіть площу ромба зі стороною 12 см і гострим кутом 30°.
   а) 144 см²; б) 36см²; в) 72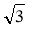 см²; г) 72 см².

Варіант 2

1. Назвіть формулу площі квадрата зі стороною а.
   а) 2а²; б) 4а;  в) а²;  г) 4а².
2. У паралелограмі ABCD до сторони AD проведено висоту ВК. Знайдіть площу паралелограма, якщо ВС = 8 см, ВК = 5 см.

а) 20 см²; б) 40 см²; в) 80 см²; г) 13 см².

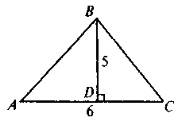
3. За даними рисунка знайдіть площу три­ кутника ABC.

а) 30;  б) 60;  в) 15;  г) 11.

4. Знайдіть площу прямокутного трикутни­ка з катетом 15 м і гіпотенузою 17 м.
   а) 127,5 м²;  б) 60 м²; в) 120 м²; г) 60 см².
5. Сторони паралелограма дорівнюють 12 см і 16 см, а менша висота – 3 см. Знайдіть більшу висоту паралелограма.

а) 4 см; б) 2,25 см;  в) 6 см; г) 14 см.

6. Знайдіть площу паралелограма зі сторонами 8 м і 12 м та гострим кутом 30°.

а) 48 м²; б) 96 м²; в) 24 м²; г) інша відповідь.

Після закінчення роботи — перевірка і корекція.

III. Формулювання мети і завдань уроку

Залежно від рівня інтелектуальної активності учнів учитель або сам повідомляє мету уроку — вивчення формули для обчислення площі тра­пеції, або ж пропонує учням виконати практичне завдання (на розви­ток конструктивного мислення).

Завдання

1.   Одного разу Петрик П'яточкін склав трапецію із чотирьох пря­мокутних трикутників. Чи зможете ви повторити його досягнення? «покращити» (тобто скласти трапецію з меншої кількості прямокутних трикутників)? Що спільного мають усі трикутники в кожному із зоб­ражених випадків?
2.   Який із випадків можливий для будь-якої трапеції?

Розв'язуючи завдання, учні можуть прийти до конфігурацій, зоб­ражених на рис. 1.

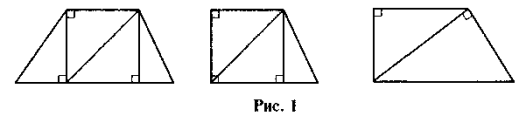
Розв'язання задачі, крім суто розвивального значення, допомагає учням зрозуміти прийом, який використовують автори підручника під час обґрунтування формули площі трапеції — розбиття трапеції на три­кутники з рівними висотами, що дорівнюють висоті трапеції, та зі сто­ронами, що є основами трапеції. Від розуміння цього факту до форму­лювання мети уроку один логічний крок — якщо застосувати власти­вості площ та формулу площі трикутника, то напевно можна вивести формулу для обчислення площі трапеції. Реалізація цього плану (з по­дальшим закріпленням виведеної формули та формуванням умінь за­стосовувати формулу площі трапеції) — основна мета уроку.

IV. Актуалізація опорних знань, та вмінь

З метою успішного засвоєння учнями змісту теореми, що виражає формулу площі трапеції, та ідеї її доведення, а також розуміння учнями можливості запису теореми у вигляді S = MN h, учням слід активізувати знання і вміння щодо аксіом площ, формули площі трикутника, означення трапеції, середньої лінії трапеції та її властивості.

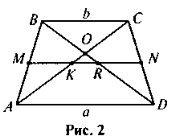1. ABCD – трапеція   (BC || AD), AD = a, BC = b, AM = BM, CN = ND. Який   із зображених  на рисунку 2 відрізків  має довжину:

а) ;  б) ;  в) ; г) ?

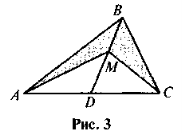
2. На медіані BD трикутника ABC (рис. 3) взято довільну точку М. Доведіть, що площі трикутників АВМ і СВМ рівні.

V. Засвоєння знань

План вивчення нового матеріалу

1. Теорема (формула площі трапеції).
2. Друге формулювання формули площі трапеції.

VI. Формування первинних умінь

Виконання усних вправ

1. Дві рівновеликі трапеції мають рівні висоти. Чи означає це, що ос­нови даних трапецій також відповідно рівні?
2. Чи може діагональ трапеції ділити її на два рівновеликі трикутни­ки? Відповідь обґрунтуйте.
3. Дано: ABCD — трапеція (BC || AD). Знайдіть 5, якщо:

а) ВС = 2 см; AD = 10 см; h = 5 см;

б) BC + AD = 16 см; h = 6 см;

в) середня лінія дорівнює 10 см; висота 5 см;

г) r = 5 см; AB + CD = 18.

Виконання письмових вправ

1. Знайдіть площу трапеції, якщо:

а) її основи дорівнюють 4 см і 10 см, а висота — 6 см;

б) висота трапеції та її середня лінія дорівнюють 8 см.

2. Основи рівнобедреної трапеції дорівнюють 8 см і 16 см, а гострий кут — 45°. Знайдіть площу трапеції.
3. Знайдіть площу:

а) рівнобедреної трапеції з основами 15 см і 39 см, діагональ якої перпендикулярна бічній стороні;

б) прямокутної трапеції з бічними сторонами 12 см і 13 см, діагональ
якої є бісектрисою гострого кута.

VII. Підсумки уроку

Яка із фігур на рис. 4 зайва? Чому?

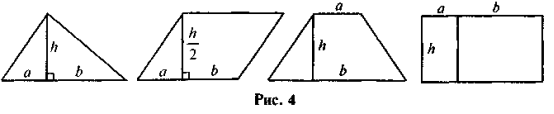
VIII. Домашнє завдання

Вивчити формулу для обчислення площі трапеції.

Розв'язати задачі.

1. Основи прямокутної трапеції дорівнюють 6 см і 10 см, а більша біч­на сторона — 5 см. Знайдіть площу трапеції.
2. Знайдіть площу рівнобедреної трапеції з основами 14 см і 50 см та діагоналлю 40 см.
3. У прямокутній трапеції сума основ дорівнює 20 см, а сума біч­них сторін — 30 см. Знайдіть площу трапеції, якщо один із її кутів дорівнює 30°.
4. Основи трапеції, вписаної в коло, дорівнюють 12 см і 4 см. Знай­діть площу трапеції, якщо в неї можна вписати коло.