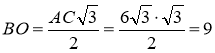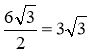Розв'язування задач про многокутники

Тема. Розв'язування задач про многокутники

Мета: закріпити та систематизувати знання учнів про:

• зміст поняття площі многокутника та його властивості;
• формули для обчислення площ прямокутника та паралелогра­ма, їх наслідки.

Відпрацювати навички застосування набутих знань.

Тип уроку: застосування знань, умінь та навичок.

Наочність та обладнання: конспекти 17, 18.

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

Як і на попередньому уроці, для економії часу учні коментують розв'язання домашніх задач за готовими рисунками, виконаними на дошці заздалегідь.

Засвоєння змісту теоретичного матеріалу та його розуміння пере­віряється під час виконання учнями математичного диктанту.

Математичний диктант

ІІІ. Формулювання мети і завдань уроку

Якість виконання домашньої роботи, а також результати виконан­ня математичного диктанту на попередньому етапі уроку дають мож­ливість вчителю сформулювати мету відповідно до ситуації: або як за­кріплення знань властивостей площ та формул площ прямокутника, па­ралелограма та продовження роботи із формування вмінь практичного застосування цих знань, або ж як доповнення знань, закріплення цих знань та відпрацювання навичок застосування знань у стандартній та в нестандартній ситуаціях.

IV. Відтворення, корекція та систематизація опорних знань

Повторення та систематизація знань учнів, набутих ними під час вивчення матеріалу підручника частково відбулося під час виконання учнями математичного диктанту. Кращого результату можна домогтися, якщо учням запропонувати виконати обернене завдання: на рис. 1 (учитель може змінити ситуації на свій смак), зображені типові ситуації (пов'язані із застосуванням вивченого в темі матеріалу), за якими учні мають скласти найбільш відповідне твердження (у математичному та словесному вигляді). Для того щоб залучити до роботи якомога більше учнів, можна організувати роботу в малих групах. Спочатку завдання виконується по групах, а потім результати виконання завдання презентуються та в разі необхідності коригуються.

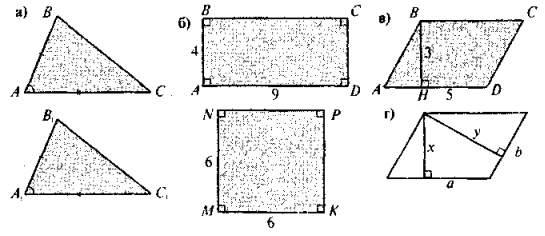
Під час презентації та корекції цього завдання вчитель може до­помогти учням «відкрити» додатково деякі цікаві співвідношення (на­приклад, рис. 1 допоможе учням «відкрити» формулу для обчислення площі ромба як половини добутку діагоналей). Такі «відкриття» (якщо вони були зроблені учнями) слід узагальнити, зафіксувати в зошитах та закріпити на відповідних задачах.

V. Застосування вмінь

Застосування знань у стандартних ситуаціях

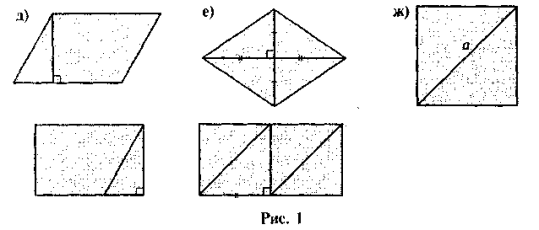
1. Нарис. 2 ABCD — квадрат. Знайдіть S_AHCD.
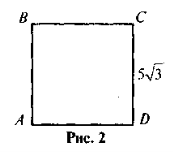
2. Нарис. 3 ABCD — паралелограм. Знай­діть S_ABCD.
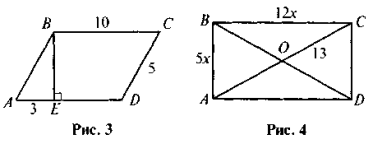
3. На рис. 4 ABCD — прямокутник. Знай­діть S_ABCD.

Застосування знань у нестандартних ситуаціях

1. Площа і периметр ромба дорівнюють відповідно 24 см² і 24 см. Знайдіть висоту ромба.
2. Діагоналі ромба дорівнюють 16 см і 30 см. Знайдіть площу чотири­кутника, вершинами якого є середини сторін даного ромба.
3. На діагоналі квадрата як на стороні побудо­вано інший квадрат. Доведіть, то його пло­ща вдвічі більша за площу даного квадрата.
4. Сторони паралелограма дорівнюють 12 см і 16 см, а одна з висот – 15 см. Знайдіть площу паралелограма.
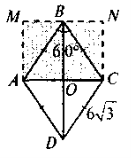
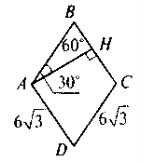
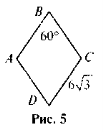
5. На рис. 5 ABCD — ромб. Знайдіть S_ABCD.

 Застосування знань у стандартних ситуаціях означає розв'язування задач, до яких подається рисунок, на якому зображено відомі величини і вид чотирикутника, тому учні мають просто вибрати серед формул відповідну та за нею знайти площу фігури. Розв'язування таких задач допомагає учням сформувати павички проводити доказові міркування із використанням вивчених тверджень.

Нестандартність ситуацій, описаних у задачах, що йдуть даті, полягає в тому, що ці задачі вимагають від учнів впевненого володіння матеріалом, вивченим як у темі «Площі. Площа прямокутника, площа паралелограма», так і в попередніх темах 7 і 8 класу (властивості ромба, середня лінія трикутника; властивість катета, що лежить проти кута 30°, метричні співвідношення в прямокутному трикутнику, а також вираження катета прямокутного рівнобедреного трикутника через його діагональ), а також нестандартного мислення (наприклад, задача № 5).

Підбиваючи підсумки цього етапу уроку, вчитель має наголосити на тому, що розв'язування будь-якої геометричної задачі неможливе без вільного володіння учнями змістом вивчених геометричних понять. а також без умінь упевнено оперувати цими знаннями.

VII. Підсумки уроку

Продовжуючи думку, висловлену вчителем на попередньому етапі уроку, учні мають провести самооцінку результатів навчальної діяль­ності на уроці.

VIII. Домашнє завдання

Повторити за підручником або конспектами зміст основних по­нять теми.

Розв'язати задачі.

1. Висота ромба з тупим кутом 150° дорівнює 5 см. Знайдіть площу ромба.
2. Точка, то лежить на діагоналі квадрата, віддалена від двох його сторін на 180 см і 2,2 м. Знайдіть площу квадрата.
3. Висоти паралелограма дорівнюють 12 см і 16 см, а кут між ними — 30°. Знайдіть площу паралелограма.

Або виконати домашню самостійну роботу.

1. Площа прямокутника зі сторонами 6 см і 10 см дорівнює площі ромба з периметром 48 см. Знайдіть висоту ромба.
2. Сторони паралелограма дорівнюють 6 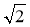см і 9 см, а кут між ними 135°. Знайдіть площу паралелограма.
3. З вершини прямокутника до діагоналі проведено перпендикуляр завдовжки 8 см. Основа перпендикуляра ділить діагональ у відно­шенні 1 : 4. Знайдіть площу прямокутника.
4. Повторити властивість діагоналі паралелограма; властивість площ рівних фігур га аксіом площ.