ПРИКЛАДНА МАТЕМАТИКА

 і не тільки…

 

 

 

 

 

 

 

 

 

 

 

Розглянуто на засіданні методичної комісії природничо-математичних дисциплін. Схвалено науково-методичною радою закладу професійно-технічної освіти. Протокол №1 від 17.01.2018р.

 

 

 

 

 

 

Панас Г.І., викладач математики

 

 

 

 

 

 

Прикладна математика і не тільки. –  ДНЗ «Нововолинський центр ПТО», 2018. – 238 с.

 

 

 

 

 

 

 

 

 

Будь-який предмет неможливо викладати на достатньому рівні, якщо він не обґрунтований практичною діяльністю. Особливо  це стосується курсу математики, де зв'язок між теоретичною частиною і її застосуванням на практиці має першорядне значення. Однією із форм здійснення цього зв’язку є розв’язування задач практичного змісту.

Під час вивчення математики в учнів часто виникає запитання: навіщо мені все це потрібно?

Зацікавити учнів математикою, показати її могутність і красу, примусити полюбити її – завдання кожного вчителя математики.

Матеріал у посібнику розподілено за розділами програми. До окремих тем  у посібнику подано короткі історичні відомості, які допоможуть підвищити інтерес учнів до математики, теоретичні відомості, які дадуть змогу пригадати визначення термінів або формули.

Наведені завдання можна пропонувати учням для індивідуального самостійного опрацювання, групової роботи, що сприятиме тренуванню соціальної спрямованості, різноманітних проектів, підготовки до дорослого життя.

ЗМІСТ

Передмова………………………………………………………………………... … 4

Застосування математики………………………………………………………….. 9

Математичне моделювання…………………………………………………….. ...10

Алгебра ……………………………………………………………………………. 12

Дійсні числа………………………………………………………………… 12

Відсоткові розрахунки…………………………………………………… ...13

Відсотки і кулінарія…………………………………………………..…16

Математика і економіка…………………………………………………20

Прогресія……………………………………………………………………..22

Пропорції……………………………………………………………………..25

Задачі на рівняння…………………………………………………………...26

Функції, їхні властивості та графіки……………………………………….28

Функціональні залежності………………………………………………28

Основні властивості функцій…………………………………………...38

Степенева функція………………………………………………………39

Приклади функціональних залежностей………………………………41

Тригонометричні функції…………………………………………………...57

Властивості і графіки тригонометричних функцій……………………66

Показникова та логарифмічна функції……………………………………..69

Показникові функція…………………………………………………….72

Логарифмічна функція. Історія виникнення…………………………...77

Похідна та її застосування…………………………………………………..84

Задача, що приводять до поняття похідної…………………………….85

Диференціювання функцій……………………………………………...88

Найбільше і найменше значення функції……………………………...88

Застосування похідної…………………………………………………..91

Інтеграл та його застосування………………………………………...........93

Первісна …………………………………………………………………95

Інтеграл…………………………………………………………………..96

Застосування інтеграла………………………………………………….97

Диференціальні рівняння………………………………………………101

Елементи теорії ймовірностей і математичної статистики……………...102

Елементи комбінаторики………………………………………………102

Поняття теорії ймовірностей…………………………………………..104

Випадкове випробовування і випадкова подія……………………….107

Відносна частота випадкової події…. ………………………………..108

Вибірковий метод у статистиці………………………………….……109

Геометрія ………………………………………………………………………….111

Основні властивості фігур…………………………………………………114

Кути …………………………………………………………………………116

Ознаки рівності трикутників………………………………………………116

Подібні трикутники………………………………………………………..117

Коло…………………………………………………………………………118

Чотирикутники. Трапеція …………………………………………………118

Теорема Піфагора…………………………………………………………..119

Декартові координати на площині………………………………………...120

Перетворення фігур………………………………………………………...122

Розв’язування трикутників………………………………………………...123

Многокутники………………………………………………………………125

Площі многокутників…………………………………………………..126

Вписані та описані многокутники………………………………….…126

Довжина кола……………………………………………………………….126

Площі фігур…………………………………………………………………129

Вступ до стереометрії……………………………………………………...131

Аксіоми стереометрії………………………………………………………133

Взаємне розміщення двох прямих у просторі……………………………135

Паралельність прямих і площин…………………………………..............137

Паралельність площин…………………………………………………….139

Перетворення фігур у просторі……………………………………………139

Паралельне проектування……………………………………………...140

Зображення фігур у стереометрії……………………………………...143

Перпендикулярність прямих і площин……………………………………143

Перпендикуляр і похила……………………………………………….146

Перпендикулярність у просторі. Застосування теореми про три перпендикуляри…………………………………………………………………...148

Зв'язок між паралельністю та перпендикулярністю прямих і площин…………………………………………………………………………….149

Перпендикулярність площин………………………………………….152

Ортогональне проектування…………………………………………...154

Вимірювання відстаней у просторі……………………………………155

Вимірювання кутів у просторі………………………………………...156

Координати і вектори у просторі………………………………………….165

Геометричні тіла і їх поверхні……………………………………………..174

Призма…………………………………………………………………..175

Паралелепіпед…………………………………………………………..179

Піраміда…………………………………………………………………179

Правильні многогранники……………………………………………..180

Тіла обертання………………………………………………………….182

Циліндр…………………………………………………………………183

Конус……………………………………………………………………187

Куля і сфера…………………………………………………………….191

Об’єми і площі поверхонь геометричних тіл…………………………….194

Задачі на знаходження об’ємів многогранників……………………..194

Об’єм кулі………………………………………………………………210

Площі поверхонь геометричних тіл…………………………………..212

Задачі на обчислення площі поверхні призми……………………….213

Комбінації тіл……………………………………………………………….220

Список використаних джерел……………………………………………..226

 

ПЕРЕДМОВА

Дуже корисно пізнати справжнє виникнення

                                                                  чудових відкриттів, особливо таких, що були зроблені  не випадково , а силою думки.

Це приносить користь не стільки тим,

що історія воздає кожному своє і  спонукає

 інших добиватися таких самих похвал,

 стільки тим, що пізнання методу на видатних                                              прикладах веде до розвитку мистецтва відкриття                                                                                                                                          Г.Лейбніц

Сучасне суспільство знаходиться у стані політичних та економічних змін. Тому для людини важливими є здатність бути мобільною та адаптивною, вміння бачити проблему, чітко формулювати та всебічно підходити до її розв’язування, здобувати необхідну інформацію тощо. Відповідно до потреб продукуються зміни в освіті, проходить її модернізація.

Національна доктрина розвитку освіти в Україні у ХХІ столітті вже зорієнтована на нове соціальне замовлення. Державний стандарт базової та повної середньої освіти визначає як основну мету освітньої галузі «Математика» опанування учнями системою математичних знань, навичок та умінь, необхідних у повсякденному житті та майбутній трудовій діяльності , достатніх для успішного оволодіння іншими освітніми галузями знань і забезпечення неперервної освіти; формування в учнів наукового світогляду, уявлень про ідеї та методи математики , про її роль у пізнанні дійсності, інтелектуальний розвиток учнів. Концепція математичної освіти школи визначає одним із пріоритетів розвитку математичної освіти необхідність посилення прикладної спрямованості математики. Важливість її реалізації підкреслено в пояснювальних записках до програм з математики для 11-річної школи.

Проблема реалізації прикладної спрямованості завжди була і є в полі зору  методистів, науковців, авторів підручників. У роботах науковців проведено теоретичне обґрунтування її існування та шляхи розв’язування. Сформульовані загальні принципи, які забезпечують шкільному курсу математики прикладну спрямованість, розроблені шляхи розв’язування завдань навчання учнів застосовувати математичні знання на практиці, визначені умови реалізації прикладної спрямованості математики у навчальних закладах.

Прикладну спрямованість розглядають як засіб активізації навчально-пізнавальної діяльності учнів, виокремлюють як одну із функцій навчання, підкреслюють її важливість для формування мотивації навчання. Частина наукових досліджень присвячена проблемі формування в учнів умінь, пов’язаних із застосуванням математики, методиці прикладної спрямованості предметів шкільної математики, зокрема. У значній кількості досліджень увага приділяється комплексному використанню засобів прикладної спрямованості : прикладних задач та інформації про походження математичних об’єктів.

Для вирішення даної проблеми важливим є формування в учнів прийомів діяльності прикладного характеру, моделювання в навчальній діяльності, використання інформаційно-комунікативних технологій, навчання учнів розв’язуванню прикладних задач, формування математичного бачення світу, використання міжпредметних зв’язків.

Варто досліджувати прикладну спрямованість математики, так як її вивчення  має вагоме значення для інтелектуального розвитку людини та водночас на існуючі проблеми математичної освіти у шкільній практиці.

Система освіти в нашій країні вступила в період фундаментальних змін, що характеризуються новим розумінням цілей освіти, новими концептуальними підходами до розробки і використання навчальних технологій  і т. ін. Тому поставлені перед навчальними закладами завдання щодо поєднання  навчання з подальшою продуктивною працею, підвищення ефективності навчання можуть бути реалізовані за умовами зміни відношення педагогів до навчального процесу, а саме підвищення   математичної освіти за умов посилення її прикладного, практичного та політехнічного спрямування.

Нові суспільні умови та нові завдання освітньої галузі «математика» потребують корекції існуючих шляхів досягнення мети та вирішення зазначеної проблеми   курсу математики. 

Важливою стороною проблеми активізації навчально-пізнавальної діяльності є насамперед соціальний аспект. У національній державній програмі «Освіта» (Україна ХХ1 століття) зазначено, що загальна середня освіта має забезпечувати продовження всебічного розвитку дитини як цілісної особистості її здібностей і обдаровань, збагачення на цій основі інтелектуального потенціалу народу, його духовності та культури, формування громадянина України, здатного до свідомого суспільного вибору. Потяг до знань, високу пізнавальну активність та уміння самовдосконалюватися необхідно розвивати й виховувати у молоді під час навчання у професійних навчальних закладах. Успішне вирішення цього завдання щонайперше створює надійні передумови для глибокого та міцного оволодіння навчальним матеріалом. Разом з цим воно забезпечує умови для наступної систематичної роботи учнів над собою, для практичної реалізації ідеї неперервної освіти і самоосвіти.

Велике значення мають також психологічні і педагогічні передумови вирішення зазначеної проблеми. Оновлення змісту освіти, приведення його у відповідність із сучасними потребами особи і суспільства вимагає вдосконалення процесу навчання. У системі навчальних занять широке застосування мають знайти найбільш ефективні методи і прийоми організації навчання учнів, що сприятимуть збудженню і розвитку в них пізнавальної активності. Учень не зможе усвідомити і зробити власним надбанням матеріал, що вивчається, якщо він не відчуває потреби в його вивченні, і не виявлятиме розумової напруги, наполегливості в навчанні. Ось чому все більшого значення набуває орієнтація на розвиток учнів шляхом створення умов для широкого аналізу фактів, на озброєння умінням самостійно працювати, вчитися самому. Проте розвиток пізнавальної активності учнів відіграє велику роль не тільки у підвищенні рівня розвитку учнів і поліпшенні якості успішності, а і в їх вихованні. Адже перетворення знань на переконання і розвиток моральної свідомості учнів досягається лише тоді, коли учні всебічно усвідомлюють матеріал, що вивчається, коли засвоєні висновки й узагальнення є результатом їхніх власних розумових зусиль і позитивних емоційних переживань. Таким чином, сам підхід до навчання і методика його організації суттєво впливають на формування інтелекту, світогляду та морального обличчя учнів.

Учнів  необхідно спеціально навчати вміння поєднувати теоретичні знання з практичними діями. При цьому включення у процес навчання питань і задач прикладного та професійного змісту є лише необхідною умовою такого навчання. Крім цього, необхідно навчати учнів спеціальних прийомів розумової роботи, що є необхідними для застосування теоретичних знань, і формувати в них практичні вміння і навички, що лежать в основі застосування математики на інших уроках, у виробництві та побуті, у майбутній професії. Проблема застосування знань на практиці вимагає формування в учнів уміння аналізувати й синтезувати ситуації, конкретизувати загальні абстрактні положення, пізнавати відомі фігури, залежності у конкретних ситуаціях, переусвідомлювати один і той самий об’єкт або явище під кутом зору різних систем знань, варіювати способи дій, переключатися з одного виду діяльності на інший.

Математика має призначення  розширити  й поглибити знання і вміння, які необхідні для математичного моделювання і дослідження процесів і явищ за допомогою функцій, рівнянь та інших математичних об’єктів , опанувати суміжними предметами (фізика, хімія, біологія тощо). І тим самим упевнитися у могутності математичних методів для пізнання навколишнього світу, у розв’язанні різних проблем.

Однією з характерних особливостей нашого часу є широке застосування науки у різних галузях діяльності людини. Без математики не обійтися при проектуванні та будівництві споруд, виробництві приладів та їхніх деталей, важливу роль відіграє ця наука у плануванні господарчої діяльності, керуванні технологічними процесами, роботою підприємств тощо.

Суттєве прискорення процесу математизації науки, техніки, господарської діяльності пов’язане зі створенням ЕОМ, автоматизацією процесів виробництва, новітніми технологіями, істотними змінами у характері праці людини.

Математика стала універсальним засобом моделювання та дослідження навколишнього світу, надійним знаряддям розв’язування практичних задач.

Вивчення математики , її застосувань є невід’ємною  складовою формування світогляду людини та підготовки сучасного фахівця – кваліфікованого робітника , техніка, інженера, економіста тощо.

Математика виникла на ранній стадії розвитку людства під впливом потреб практики. Розвиток ремесла, землеробства, торгівлі й обміну, навігації, управління державою потребував удосконалення вимірювань і розрахунків. Вона послуговується досить загальними і чіткими об’єктами для описання навколишніх явищ (геометричні фігури, числа, рівняння, вектори і т.д.). Вченими розроблено низку потужних методів дослідження математичних об’єктів : метод координат, алгебраїчні методи, методи математичного аналізу й ін…

Математика є зручним і ефективним засобом для описання і дослідження закономірностей реальності.

 

 

 

 

 

 

 

Застосування математики

 Математика— найдавніша з усіх наук, проте вона

 залишається наукою вічно молодою,

яка бурхливо розвивається, весь час розширює

 галузі свого пізнавання, все ширше розвиває

свої зв’язки не тільки з природничими науками,

а й з найрізноманітнішими галузями людської діяльності.

М.В. Келдиш

Хоч би яку науку ми не вивчали, хоч би в якій галузі виробництва ми не працювали, якщо ми хочемо залишити після себе слід, необхідні знання математики. Всі професії вимагають доброго знання математики. Всі ми хочемо брати участь у великому житті – розбудові України. І тому нам потрібно якнайбільше знати про практичне застосування математики в різних галузях виробництва і в житті. В майбутньому вона нам дасть величезну допомогу в усіх наших справах.

Визначні досягнення у всіх сферах економічного і суспільного розвитку ґрунтуються на всебічному застосуванні природничих наук і насамперед математики. Вона допомагає сьогодні розв’язувати також господарські проблеми.

У всіх галузях практичної діяльності людини, навіть у таких традиційно “нематематичних”, як управління виробництвом, біологія, медицина, лінгвістика, надійно й ефективно застосовується математика.

Який зв’язок між математикою і об’єктивною реальністю? Завдяки чому числа, геометричні фігури та інші математичні поняття можуть відбивати й описувати найрізноманітніші явища навколишньої дійсності, передбачити закономірності їх перебігу?

  Видатний педагог В.О.Сухомлинський писав, “… математика – це насамперед думка, допитлива, що бажає все знати, про все мати уявлення. Математика вчить мислити й разом з тим вселяє віру в безмежні сили людського розуму. Вона виховує волю, характер”.

Для чого потрібна математика на роботі? Яку не візьми професію, вона пов'язана з математикою.   Без знання цього предмета люди не літали б в космос, не водили б машини, трамваїв, метро та багато іншого. В лікарні  не можливо обійтися без знання математики. Потрібно хворому виміряти тиск , якщо не знаєш цифр не можеш це зробити. Якщо хворе серце , щоб порахувати пульс необхідно знати , що таке хвилина, секунда , година. Навіть укол не зробиш без знання математики. Та багато іншого. Професія  будівельника теж має відношення до математики. Як збудувати будинок? Скільки потрібно цеглин? Як зробити заміс з води, піску,цементу? В якій пропорції? В будівництві це дуже важливо. Як зробити дах? Під яким кутом? При цьому необхідно знання з геометрії. Та багато-багато іншого. Щоб збудувати будинок необхідно знати скільки потрібно цегли, піску, цементу та багато іншого...  Цей предмет має дуже важливе знання у нашому житі. Особливо в наш вік, коли все пов'язано з електронікою, комп'ютерами. Тому мабуть цей предмет і є самим тяжким порівняно з іншими предметами.

Математичне моделювання

Застосування математики для описання і дослідження процесів  та явищ дійсності ставить нас перед необхідністю знайти відповідь на запитання: «В чому полягає сутність розв’язання прикладної задачі за допомогою математики?»

Часто доводиться застосовувати математичні знання для розрахунку швидкості  заповнення басейну, часу виконання роботи та ін.. Ці застосування передбачають заміну реальних об’єктів і відношень між ними математичними об’єктами і відношеннями між ними (функціями, рівняннями, геометричними фігурами).

Для цього необхідно передусім виділити суттєві характеристики реальних об’єктів і відношень між ними, і саме їх замінити математичними об’єктами і зв’язками між ними. Процес такого заміщення називається математичним моделюванням.

Основним методом реалізації прикладної спрямованості шкільного курсу математики є метод математичного моделювання, а найбільш ефективним засобом – прикладні задачі, розв’язування яких потребує глибоких знань як  з математики,так і з інших дисциплін.

Усі наші знання про навколишній світ уявляються у вигляді найрізноманітніших моделей, серед яких є і математична.

Математичними моделями прийнято називати системи математичних об’єктів, що описують досліджуваний процес або явище математичною мовою. Для складання математичних моделей використовують різноманітні математичні засоби: рівняння, функції, графи, таблиці, геометричні конструкції тощо. У моделі концентрується сукупність наших знань, уявлень , гіпотез про відповідний об’єкт чи явище. Оскільки  ці знання ніколи не бувають абсолютними, а гіпотези можуть іноді навмисне не враховувати деякі факти, то модель лише наближено  описує поведінку реальної системи. Заміна вже наявних моделей на ті, в яких повніше відтворюються суттєві для дослідження властивості процесу чи явища, , комбіноване застосування різних моделей – шлях пізнання дійсності.

У процесі розв’язування прикладної задачі звичайно виникає потреба побудови математичних моделей реальних об’єктів, про які йдеться у задачі. Математичні моделі реального процесу або об’єкта можуть бути подані у вигляді формули, математичного малюнка, математичного твердження, геометричної фігури. У реальному житті є багато задач, які, на перший погляд , не мають між собою нічого спільного. Але часто для їх розв’язання можна використовувати одну й ту саму математичну модель. Отже, вміння працювати з однією математичною моделлю дає можливість розв’язувати різні прикладні задачі. Навчання учнів самостійно здійснювати дослідження, використовувати нестандартні підходи до розв’язування задач сприяє результативному та ефективному процесу формування творчого мислення учнів, підвищення навчально-пізнавальної діяльності.

Можна навести приклад  задачі, яка ілюструє застосування методу  математичного моделювання на практиці.

ЗАДАЧА. По один бік шосе знаходяться два населених пункти. Де варто збудувати автобусну зупинку?

Процес математичного моделювання загалом складається з трьох етапів:

1. вибір чи побудова математичної моделі для описання даної задачі;
2. дослідження побудованої моделі, тобто розв’язування математичної задачі;
3. тлумачення результатів дослідження, встановлення відповідності одержаного результату цілям досліджень.

При необхідності уточнюється сама математична модель і результати які з неї випливають.

Метод математичного моделювання виходить з практики, створюючи математичні моделі явищ і процесів, і повертається до неї, щоб обґрунтувати доцільність створення моделі.

АЛГЕБРА

Дійсні числа

          ЗАДАЧА. В їдальню привезли  кг зелені: петрушки, сельдерею, і кропу. Петрушки і сельдерею разом кг. Скільки кг петрушки, сельдерею, і кропу привезли окремо?

ЗАДАЧА. Вихід масла із вершків становить маси вершків, а вихід вершків з молока становить маси молока. Скільки потрібно взяти молока, щоб дістати 1ц масла?

ЗАДАЧА. Із 45кг пшениці одержали 24,3кг борошна. Скільки борошна одержать із 135кг пшениці?

ЗАДАЧА.Із 85кг свіжих вишень одержали 44,4кг сушених. Скільки потрібно взяти свіжих вишень, щоб одержати 11,1кг сушених?

ЗАДАЧА.Із 55кг чайного листу одержують 2,3кг чаю. Скільки чаю одержать із 275кг чайного листу?

          ЗАДАЧА. На початку року на хлібокомбінат постачали 75 т муки, а на кінець її кількість збільшилась на . Скільки тонн муки стали постачати наприкінці року?

ЗАДАЧА. Виконуючи денну норму, пекар заробляє 5,3 крб. Скільки заробить він за 28 робочих днів, якщо перевиконуватиме норму в 1,7 раза?

ЗАДАЧА. Мама дала Сергію 20 грн. та доручила купити молока, кефіру та сметани. Сергій купив 3 пакети молока за 1,70 грн., 2 пакети кефіру за 2,10 грн. та пакет сметани за 3,60 грн. Скільки коштів у нього залишилося?

ЗАДАЧА. На м’ясокомбінаті за день надійшло 20 000 кг м’яса. частина його пішла на виробництво ковбаси; на сосиски, а решту переробляють на паштет  і розфасовують у банки. Скільки півлітрових банок потрібно м’ясокомбінатові щодня, якщо одна банка містить 0,5 кг?

ЗАДАЧА. На заповнення банок зеленим горошком перша робітниця витратила на 3 години менше, ніж друга. Працюючи одночасно, вони закінчили роботу за 6год 40 хв. Скільки часу необхіднобуло б затратити кожній з них на заповнення всіх банок горошком?

Відсоткові розрахунки

Відсоткові обчислення широко застосовуються в реальному житті.

На виробництві у відсотках звітують про виконання завдання чи замовлення, виражають зміну продуктивності праці; при обчисленні складу різних сплавів або розчинів надають відсотковий  вміст речовини-компонентів; у мете реології у відсотках виражають вологість повітря. При розробці корисних копалин вміст чистого металу в руді виражається у відсотках від кількості руди; при випічці хліба у відсотках вказують припічку, яку одержують під час випікання, і т. ін. Особливо часто відсотками послуговуються при грошових розрахунках.

У практичній діяльності розрізняють три типи задач на відсотки: знаходження відсотків від даного числа, знаходження числа за його відсотком, знаходження відсоткового відношення двох чисел.

ЗАДАЧА. Продуктивність праці збільшилася на 25%. На скільки відсотків зменшився час, необхідний для виробництва деталі?

ЗАДАЧА. Ціна товару підвищилася на 20%, потім нова ціна зменшилася на 17%. Як у підсумку змінилася ціна відносно початкової?

ЗАДАЧА. Книжковий магазин сплачує видавництву 90% вартості, позначеної на обкладинці книги, а реалізує книгу за зазначеною ціною. Скільки відсотків складає націнка магазину?  

ЗАДАЧА. Знайти 32% від 120га.

ЗАДАЧА. Для хімічного прополювання рослин використовують гербіциди. Якщо неправильно користуватися цими препаратами, то можна дуже забруднити навколишнє середовище.

ЗАДАЧА. Гербіцид 2М-4x складається з 80% сильнодіючої отрути і застосовується для боротьби з бур’янами в посіві льону. Для цього гербіциду – 900г діючої речовини на 1 га. Препарат розчиняють у воді з розрахунку 400л на 1га. Яка кількість даного препарату треба розчинити в 100л води.

ЗАДАЧА. Відомо, що 15% площі підлоги в кімнаті дорівнює 9м². Яка площа всієї підлоги?

ЗАДАЧА. Для фарбування підлоги з розмірами 12,0мх4,0м витратили 5,28 кг фарби. Скільки фарби потрібно для фарбування підлоги кімнати з розмірами 5,2мх4,6м? Обчислення проведіть з точністю до 0,1кг.

ЗАДАЧА. Бригада будівельників в складі 6 чоловік виконує штукатурні роботи. Протягом перших 5 днів оштукатурено 300м², що складає 205 всієї площі.  За  скільки днів бригада оштукатурить всю площу?

ЗАДАЧА. У відділі технічного контролю (ВТК) заводу вимірюють діаметр вала з точністю до 0,1мм. Згідно з таблицею допусків, діаметр вала повинен задовольняти умову 167,8мм≤d≤168мм. Чи забракує ВТК вал, якщо за результатами вимірювань його діаметр дорівнює: 1) 168,1мм; 2) 167,6мм;    3) 168,0мм; 4) 168,4мм?

ЗАДАЧА. Відомо , що при використанні у вантажних автомобілях шин із капроновим кордом витрата пального зменшується на 15% у порівнянні з тим, коли використовуються шини із звичайним віскозним кордом. Для вантажних перевезень використовували 6 машин із звичайними шинами і 4 машини із шинами із капронового корду. Загальна витрата пального склала 90т. Визначте економію пального за умови , що усі машини будуть оснащені шинами із капроновим кордом. Скільки  додаткових машин можна використати для вантажних перевезень? На скільки процентів при цьому збільшиться об’єм перевезень?

ЗАДАЧА. В автопарку 180 автомобілів, з них 117 – вантажні. Скільки відсотків усіх автомобілів становлять вантажні?

ЗАДАЧА. Швидкість руху автомобіля спочатку знизилася на 20%, а потім зросла на 20%. На скільки відсотків змінилася початкова швидкість руху автомобіля?

ЗАДАЧА. За першу поїздку на автомобілі було витрачено 10% бензину, за другу – 25% того, що залишилося. Після двох поїздок залишилося бензину на 13 літрів менше, ніж було спочатку. Скільки літрів бензину було до поїздок?

ЗАДАЧА. На одній із шахт видобуток вугілля гідравлічним способом дозволив різко підвищити процент видобутку вугілля із вугільних пластів, що забезпечило виконання планового завдання (2100т)не за 6год, а за 4,5год. Транспортування вугілля по трубопроводах зберегло додатково 3,5% вугілля. На скільки збільшився видобуток вугілля за зміну за рахунок впровадження прогресивної технології і гірничотранспортного обладнання.

ЗАДАЧА. Кам’яне вугілля містить у середньому 80% вуглецю, а торф-56%. Скільки потрібно взяти торфу, щоб маса вуглецю у ньому була такою, як у 2т вугілля?

ЗАДАЧА. За 15м тканини одного виду та 20м другого заплатили 2208грн. Скільки заплачено за тканину кожного виду, коли відомо, що ціна одного метра тканини першого виду на 12% більша від ціни одного метра тканини другого виду.

ЗАДАЧА. Вартість сукні, яку хоче придбати дівчина, становить 420 грн. Перед святами вартість сукні буде зменшенона 15%.

1. Скільки грошей зекономить дівчина, якщо придбає сукню перед святами?
2. Скільки коштуватиме вподобана дівчиною сукня після знижки?
3.     Скільки відсотків становитиме початкова вартість сукні від її вартості після знижки з точністю до одиниць?

Відсотки і кулінарія

Ніхто не сумнівається, що без математики не обійтись і тут. Ось декілька прикладів практичних задач, що ними часто користуються не лише в харчовій  промисловості, але й в консервуванні овочів та фруктів, в приготуванні страв, випічці тортів.

ЗАДАЧА. Випуск цукерок на кондитерській фабриці за перший рік зріс на 5%, а за другий – на 8%. Як зріс випуск продукціїна заводі за ці два роки?

ЗАДАЧА. В одному мішку крупи на 2%  менше, ніж у другому. На скільки відсотків у другому мішку крупи більше, ніж у першому?

ЗАДАЧА.Борошно подешевшало на 14%.Скільки кілограмів його можна купити за ті самі гроші , за які раніше купували 150кг?

ЗАДАЧА. З пшениці одержують 80% борошна. Скільки пшениці треба переробити, щоб дістати 50кг борошна?

ЗАДАЧА. При випіканні хліба на 5 кг борошна припадає 2кг припічки. Скільки відсотків складає припічка : а) від маси борошна; б) від маси хліба?

ЗАДАЧА. Оскільки маса борошна, витраченого на випікання хліба, складає 75% від загальної маси спеченого хліба,  то із 6кг борошна дістали х кг хліба. Знайти х.

ЗАДАЧА. Раніше 3кг рису коштувало стільки, скільки тепер коштують 2кг. На скільки відсотків подорожчав рис?  

ЗАДАЧА. Три літри 30%-го розчину спирту змішали з 5 літрами 20%-го розчину спирту. Яким стала відсоткова концентрація спирту в утвореному розчині?

ЗАДАЧА. Маса курячого яйця дорівнює 58г. Білок складає 55,8% від загальної маси, жовток -31,9%, шкаралупа -12,3%. Якою є маса кожної з цих складових?

ЗАДАЧА. М'ясо при варінні втрачає 35% своєї маси. Визначити масу 2 кг м’яса після варіння.

ЗАДАЧА. Враховуючи , що під час варіння м'ясо втрачає 35% своєї ваги, для приготування 260 порцій вареного м’яса по 40г у кожній порції портібно було взяти х кг сирого м’яса. Знайти х.

ЗАДАЧА. При приготуванні пюре із вишень, 18% їх іде у відходи. Скільки треба взяти вишень, щоб приготувати 16,4 кг пюре?

ЗАДАЧА. Коли мелють пшеницю, то одержують борошно, манні крупи і висівки. Маса борошна становить 4/5 маси пшениці, маса манних крупів становить 1/40 маси борошна. Скільки манної крупи можна одержати якщо змолоти 5ц пшениці?

ЗАДАЧА. При приготуванні пюре із слив,28% їх іде у відходи. Скільки треба взяти слив, щоб приготувати 28,8 кг пюре?

ЗАДАЧА. У 80 кг картоплі міститься 14 кг крохмалю. Скільки треба взяти такої картоплі, щоб мати 21кг крохмалю?

ЗАДАЧА. З 20 кг яблук виходить 16 кг яблучного повидла. Скільки яблучного повидла вийде з 45 кг яблук?

ЗАДАЧА. Коли готують пюре із слив, 28 % їх іде у відходи. Скільки треба взяти слив, щоб приготувати 28,8 кг пюре? 

ЗАДАЧА. Із свіжих слив одержують 32% сушених. Скільки взяли свіжих слив, якщо одержали 8кг сушених?

ЗАДАЧА. 26кг рису містять 19,5кг крохмалю. Знайти відсотковий вміст крохмалю в рисі.

ЗАДАЧА.У 36кг сої міститься 7,2кг жирів. Знайти відсотковий вміст жиру в сої.

ЗАДАЧА. Рис містить 75% крохмалю, а ячмінь-60%. Скільки потрібно взяти ячменю, щоб мати стільки крохмалю, скільки його в 5кг рису?

ЗАДАЧА. У насінні льону міститься 47% олії. Скільки льняної олії можна дістати з 350кг насіння льону?

ЗАДАЧА. Для виготовлення соку беруть 12 частин ягід і 17 частин води. Скільки ягід їм потрібно взяти, щоб отримати 232 кг соку?

ЗАДАЧА. З молока виходить 10% сиру. Скільки треба молока, щоб вийшдо 50кг сиру?

ЗАДАЧА. З молока виходить 20% вершків, а з вершків – 25% масла. Скільки треба молока, щоб одержати 100кг масла?

ЗАДАЧА. Із молока, жирність якого становить 5%, виготовляють сир жирністю 15,5%, при цьому залишається сироватка жирністю 0,5%. Скільки сиру виходить із 1 т молока?

ЗАДАЧА. Уміст води в 100кг сухого молока становить 7%. Якщо до цих 100кг долити води, то дістанемо молоко, в якому вода становить 60%. Скільки треба добавити води?

ЗАДАЧА. Скільки кілограмів молока треба взяти для здобуття 483кг масла, якщо молоко дає 21% вершків, а вершки – 23% масла?

ЗАДАЧА.Із цукрових буряків виходить  15% цукру. Скільки буряків потрібно переробити, щоб вийшло 3т цукру?

ЗАДАЧА. Морська вода містить 6% солі. Скільки води потрібно взяти, щоб отримати 42 кг солі?

ЗАДАЧА. Малина під час сушіння втрачає 75% своєї маси. Скільки свіжої малини потрібно висушити, щоб мати 5кг сушеної малини?

ЗАДАЧА. Вологість агруса зменшмлася з 99% до 98%. На скільки % зменшилася його маса?

ЗАДАЧА. Свіжі гриби містять 90% води, а сухі-12%. Скільки треба висушити свіжих грибів, щоб одержати 25кг сухих?

ЗАДАЧА.Вологість свіжих грибів дорівнювала 99%. Коли гриби підсушили,їх вологість зменшилася до 98%. Як змінилася маса грибів?

ЗАДАЧА. Свіжі гриби містять 90% води, а сухі-12%. Скільки вийде сухих грибів з 22кг свіжих?

ЗАДАЧА. Під час сушіння гриби втрачають 92% своєї ваги. Скільки свіжих грибів потрібно взяти, щоб отримати 6 кг сушених?

ЗАДАЧА. На складі було 100кг грибів. Аналіз показав, що в них міститься 99% води. Через деякий час аналіз показав, що вміст води складає 98%. Скільки стали важити гриби?

ЗАДАЧА. До розчину, який містив 20 г солі, додали 100 г води, після цього концентрація розчину зменшилась на 10%. Скільки грамів води містив розчин спочатку?  

ЗАДАЧА. До розчину, що містить 40 г солі, додали200 г води, після цього його концентрація зменшилась на 10%. Скільки води містив розчин і яка була його концентрація?

ЗАДАЧА. Скільки солі міститься в 10кг 7%-го сольовогорозчину?

ЗАДАЧА. Нектар містить 70% води, а одержаний з нього мед -17%. Яку кількість нектару повинні переробити бджоли для одержання 1кг меду?

ЗАДАЧА. Щоб одержати 4,4кг смаженої кави, необхідно взяти х кг свіжої кави, оскільки під час смаження кава втрачає 12% своєї ваги. Знайти х.

ЗАДАЧА. Є 90г 80% оцетової есенції. Яку найбільшу кількість 9% столового оцту з неї можна отримати?

ЗАДАЧА. За сніданком дівчина  приготувала для сестри 100 грамів чаю з 15 грамами цукру. Але сестрі, яка намагається схуднути і яка ретельно перевіряє вміст цукру в кожному продукті, чай видався занадто солодкий, тож вона попросила сестру долити ще води, щоб відсотковий вміст цукру в чаї став рівно 5%.

1. Скільки  грамів води потрібно долити дівчині?
2.     Скільки грамів цукру повинен містити  чай при різній кількості долитої води, щоб вміст цукру був сталим – 5%?

ЗАДАЧА. Індійський чай дорожчий від грузинського в 5/4 раза. В яких пропорціях потрібно змішати індійський чай  з грузинським, щоб дістати чай, який дорожчий за грузинський у 6/5 раза?

Математика та економіка

Кожен з нас повинен формувати у себе економічне мислення, готуватись до адаптації в умовах розвитку ринкової економіки. Неодмінною складовою ринкової економіки є добре розвинута банківська система. Основою господарювання банків є їхня відсоткова ставка, яка дозволяє одержувати прибутки. Застосовуються у банківських операціях формули простих і складних відсотків.

Відсотки широко застосовують у фінансових операціях (прибутки з капіталу, сплата внесків, різні касові операції та ін.).

У кожній державі діють тисячі комерційних банків, роботу яких контролює один або кілька центральних. Центральний банк встановлює частку вкладів, яка обов’язково повинна бути в резерві банку у вигляді готівки. Решту грошей (вільні резерви) можна надавати в кредит під визначені відсотки. З цих прибутків вкладникам виплачують відсотки за користування їхніми грошима. Частка резервів як правило коливається від 5% до 25%.

Q_t=Q₀(1+pt/100) – формула простих відсотків, Q₀ – первинний вклад, p - банківська ставка , t –роки.

Q_t=Q₀(1+p/100)^t – формула складних відсотків, Q₀ – первинний вклад, p - банківська ставка , t –роки.

ЗАДАЧА. Батько втрішив назбирати грошей, щоб придбати автомобіль. Маючи певну суму грошей, він пішов у банк. Ознайомившись з усіма депозитами, вирішив покласти гроші під 20% річних.

1.     Скільки грошей потрібно батькові внести до банку, щоб через 5 років у нього на рахунку було 497664грн?
2.     Яка сума буде у батька, якщо він отримані гроші покладе ще на один рік під 10% річних?

ЗАДАЧА. Відомо, що банківська ставка становить 30%, а первинний вклад 1000гр. Визначити суму вкладу за 5 років, якщо банк працює за формулою складних відсотків.

ЗАДАЧА. Відомо, що банк працює за формулою складних відсотків і вкладник, поклавши в банк 1000гр за 5 років отримав 2500гр. Якою була відсоткова ставка банку?

ЗАДАЧА. Клієнт взяв в банку кредит в розмірі 50 000 грн. на 5 років під 20% річних. Яку суму клієнт повинен повернути банку в кінці року?

ЗАДАЧА. Два приятелі поклали в банк по 10000 грн. кожен, причому перший поклав вклад з щоквартальним нарахуванням 10%, а другий – щорічним нарахуванням 45%. Через рік приятелі отримали кошти разом з нарахованими процентами. Хто отримав більший прибуток?

ЗАДАЧА. Деяка сума грошей знаходилась в касі ощадного банку під 2% річних (прості відсотки). Через деякий час ця сума була взята разом з нарахованими відсотками, що склало 8502 грн. Якщо б ця сума була отримана під три відсотки річних, але строком на 1 рік менше, то відсоткові гроші з неї склали б 819 грн. Яка була сума грошей, що поклали в ощадний банк, і який час вона там знаходилась.

ЗАДАЧА. Приріст продукції на підприємстві порівняно з попереднім роком склав за перший рік а%, за другий b%. Яким повинен бути відсоток приросту продукції за третій рік, щоб середній річний приріст продукції за три роки дорівнював с%?

Відповідь:%.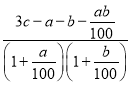

ЗАДАЧА. Дві суми складають 10000 грн. Відсоткова такса для кожної сума дорівнює 0,001, а загальна сума прибутку складає 580 грн. Знайти кожну суму окремо.

ЗАДАЧА. Громадянин С. зі свого вкладу (3%) у касі ощадбанку витрачає на кінці кожного року по 90 грн. з кожної тисячі. Через який час він витратить весь вклад?

ЗАДАЧА. На ощадну книжку було покладено 1200 грн. Через рік з книжки зняли 240 грн. Ще через рік на книжці стало 1071 грн. Скільки відсотків в рік нараховує каса?

ЗАДАЧА. Вкладник поклав до банку 1000 грн. За перший рік йому нарахований відсоток річних, який другого року збільшений на 2%.У кінці другого року на рахунку було 1188 грн. Скільки відсотків становила банківська ставка першого року?

 ЗАДАЧА. Строковий вклад, внесений до ощадного банку,щорічно збільшується на 3%. Яким стане вклад через 3 роки, якщо на початку він становив 800 грн?

 ЗАДАЧА. Обчислити сумарний об’єм кредитів, який виданий системою із шести банків, якщо обов’язкові резерви становлять 20% і внесений вклад 1000000 грн.

ЗАДАЧА. До першого банку системи, яка складається з десяти банків, внесений вклад 5000 грн. При нормі обов’язкових резервів, що дорівнює 12%. Знайти величину вільних резервів першого банку та величину обов’язкових резервів четвертого банку.

ЗАДАЧА. Будівельна компанія взяла у банку кредит 1250000грн на 3 роки під простих 15%. Визначте:а) скльки гривень компанія поверне банку через 3 роки;б) який прибуток одержить банк?

 

Прогресії

Спектр використання функцій в економіці дуже великий – від найпростіших лінійних функцій до функцій, які отримані за деяким алгоритмом,що зв’язує рекурентні відношення досліджуваних об’єктів у різні періоди часу. Періодичність ряду економічних процесів, їх коливання дозволяють використовувати також і тригонометричні функції.

Найбільш часто в економіці використовують функції:

• функція попиту – залежність об’єму попиту,  пропозиції і потреб на різні товари та послуги від ціни, доходу і т.д.;
• функція корисності – в широкому розумінні залежність корисності або результату, ефекту дії від інтенсивності цієї дії;
• виробнича функція-залежність результату виробничої діяльності від факторів, що її зумовлюють;
• функція випуску – залежність об’єму виробництва від матеріальних ресурсів та попиту;
• функція витрат – залежність витрат виробництва від об’єму продукції.

У зв’язку з тим, що економічні процеси та явища зумовлюються дією різних факторів, для їх дослідження широко використовують функції багатьох змінних. Якщо у системі координат побудувати криві попиту і пропозиції, то ці графіки дадуть можливість встановити ринкову ціну даного товару за умов конкурентного ринку.

При розв’язуванні даних задач потрібно знати формулу суми членів геометричної прогресії та знаходити відсоток від числа.

На токарних станках можна побачити таблички, на яких позначено  швидкість  обертання шпинделя для різних положень ручки. На перший погляд, ці числа здаються випадковими. Серед них є парні (20 і 40), непарні (25 і 63), дробові (31,5). Виконавши ділення кожного числа таблички на попереднє, дістанемо одне й те саме число 1,26. Виявляється, шпиндель обертається не з випадковими швидкостями, а  цілком закономірно (геометрична прогресія).

Коли конструктори-верстатобудівники ще не знали такої властивості, то, вибираючи проміжні ступені швидкості шпинделя, вони були часто безпорадними. Одні встановлювали ці ступені на однакових відрізках один від одного, інші – на нерівних без усякої закономірності. Проте жоден із способів не давав позитивного результату під час експлуатації верстата. Крім того, довільно складені швидкості утруднювали конструювання коробки передач і ускладнювали обслуговування верстатів.

У 1876р. академік А.В.Гадолін на підставі точних математичних розрахунків довів, що верстати слід будувати зі ступенями швидкостей, які утворюють геометричну прогресію.

Був час, коли кожний конструктор на свій розсуд визначав розміри деталей, вузлів створюваних ним машин. Такий різнобій дорого обходився виробникам і споживачам. Адже майже для кожної машиши потрібно виготовляти інструменти, які за своїми  параметрами не підходять до інших машин. Це саме стосується деталей, запасних частин. На основі математичних досліджень та розрахунків встановлено, що послідовності відповідних числових значень таких величин, як довжина, площа, допуски, зусилля, є членами геометричної прогресії. У техніці такі геометричні прогресії називають нормальними рядами. Ці ряди занесено до спеціальної таблиці ГОСТ-56.

За законами нормальних рядів побудовано розмірність металорізальних верстатів та металорізальних інструментів, встановлено нормальні діаметри і довжини в машинобудуванні. Єдиний метод вибору градації параметрів і розмірів окремих числових зарактеристик продукції встановлено і для інших галузей промисловості. Так, за законами нормальних рядів встановлюється ширина тканини, що дає можливість покращити економічність їх використання та визначити прогресивні параметри і габаритні розміри текстильного обладнання.

Тому геометрична прогресія становить математичну основу стандартизації різноманітної промислової продукції.

В архітектурі, будівельній справі широко використовуються колони. Виявляється, вони мають форму не циліндра, як здається на перший погляд, а зрізаного конуса.

Будівельники знають, що сила тиску в горизонтальних  шарах будівельної колони зростає в напрямку до нижньої основи. Для збереження рівноміірності напруги від тиску вздовж усієї довжини колони потрібно збільшувати площі її поперечних перерізів. Встановлено, що площі поперечних перерізів , рівновіддалених один від одного, становлять геометричну прогресію.

Враховуючи таку закономірність, колони будують не тільки красивими, а й міцними та надійними.

Оскільки площі поперечних перерізів колони збільшуються у напрямку до її основи, то колона не може мати форму циліндра.

Пропорції

Слово «пропорція» (лат. proportio)  означає «пропорційність», «певне співвідношення частин між собою».

Вчення про відношення і пропорції особливо успішно розвивалося в ІVст. до н.е. у Древній Греції, яка славилася своїми творами мистецтва, архітектури, розвитком ремесел. З пропорціями пов’язувалися уявлення про красу, порядок і гармонію,співзвучність акордів у музиці. Теорія відношень і пропорцій була викладена у «Началах» Евкліда. Там наводиться й доведення основної властивості пропорції.

Від сивої давнини люди користувалися різноманітними важелями. Весло, лом, ваги, ножиці, гойдалки, тачки – це приклади важелів. Виграш, який дає важіль під час зусилля, що докладається, визначається пропорцією     , де М і т – маси вантажів, а L  i l – «плечі важеля».

У  математиці існує словосполучення  «золотий переріз».

При розв’язуванні багатьох практичних і виробничих завдань людина використовує поняття  і правило пропорції. 

ЗАДАЧА. Господиня варить вишневе варення. На три склянки вишень вона кладе 2 склянки цукру. Скільки цукру потрібно покласти на 12 склянок вишень?

ЗАДАЧА. У 800 г розчину міститься 50г солі. Скільки солі в 240г розчину?

ЗАДАЧА. Із 36ц буряків одержали 7,2ц цукру. Скільки цукру вийде з 52ц цукрових буряків?

ЗАДАЧА. Молоко налили у 8 бідонів місткістю по 40л. Скільки потрібно двадцятилітрових бідонів, щоб розлити це молоко?

ЗАДАЧА. Скільки обертів зробить шестерня з 36 зубцями, якщо шестерня, яка з нею зчеплена, має 18 зубців і робить 60 обертів?

ЗАДАЧА. 35кг яблук засипали в два ящики у відношенні 3:4. Скільки яблук у кожному ящику?

ЗАДАЧА. У трьох ящиках 55,2кг огірків. Скільки огірків у кожному ящику, якщо їх кількість була у відношенні 3:4:5?

ЗАДАЧА. Два шківи з’єднані пасовою передачею. Один шків робить за хвилину 560 обертів, а другий – 240. Знайти обвід другого шківа, якщо обвід першого дорівнює 0,36м.

ЗАДАЧА. Два шківи з’єднані пасовою передачею. Обвід першого шківа 28см, а другого 42см. Скільки обертів за хвилину зробить другий шків, якщо перший робить 600 обертів за хвилину?

ЗАДАЧА. Шестерня з 18 зубцямт робить 24 оберти за хвилину. Скільки обертів за хвилину зробить шестерня з 36 зубцями?

ЗАДАЧА. Для перевезення вантажу потрібно 18 автомобілів вантажопідйомністю 4,5т. Скільки  потрібно автомобілів вантажопідйомністю 7т для перевезення цього вантажу?

ЗАДАЧА. Після того, як з бака вантажного автомобіля перелили в бак автобуса 40л дизельного палива, у баці автомобіля залишилося палива в 6 разів менше ніж стало в баці автобуса. Якби замість цього з бака автобуса перелили в  бак автомобіля 10л палива, то в них було б палива порівну. Скільки пального було в баках автобуса і автомобіля спочатку?

ЗАДАЧА. 180т вугілля засипали у три вагони у відношенні 1:2:3. Скільки вугілля в кожному вагоні?

Задачі на рівняння

З метою формування в учнів громадянської і соціальної компетентності бажано пропонувати учням задачі прикладного змісту на складання рівнянь. Складаючи рівняння за умовою текстової задачі, учні формують математичні моделі реальних процесів. Розв’язування таких задач демонструє учням важливість вивчення маетматики та можливості саме за допомогою знань виконувати завдання, які стосуються роботи підприємств, домашнього господарства.

ЗАДАЧА. Костюм на 119грн. дешевший за пальто. Скільки коштує костюм, якщо пальто в 1,7 раза дорожче за костюм?

ЗАДАЧА. У трьох сувоях 125м шовку. В другому сувої в 2 рази більше шовку, ніж у першому, а в третьому – на 25м більше, ніж у першому. Скільки метрів шовку у кожному сувої?

ЗАДАЧА. На пошиття 45 костюмів і 40 пальт витратили 235м сукна. На кожний костюм витратили на 0,5м сукна більше, ніж на пальто. Скільки сукна пішло на костюм і скільки на пальто?

ЗАДАЧА. У більший бідон вміщається на 2л молока більше, ніж у менший. А в два більших бідони вміщається стільки молока, скільки в три менших бідони. Скільки літрів молока входить у більший та менший бідон окремо?

ЗАДАЧА. В одному мішку було в 3 рази більше борошна, ніж у другому. Після того як з першого мішка взяли 15кг борошна, а з другого – 5кг, у першому мішку стало на 25 кг борошна бідьше, ніж у другому. Скільки борошна було у кожному мішку спочатку?

ЗАДАЧА. У першій бочці 75л олії, а в другій 160л. З другої бочки продали в три рази більше олії, ніж з першої, тоді в першій  олії залишилося в 2 рази більше, ніж у другій. Скільки олії продали з кожної бочки?

ЗАДАЧА. В одному овочесховищі 21т картоплі, а в другому 18т. У перше овочесховище щодня привозили по 9т картоплі, а в друге – по 12т. Через скільки днів у першому овочесховищі картоплі буде в 1,2 раза менше, ніж у другому?

ЗАДАЧА. У трьох посудинах було 42л мастила. В першій посудині було в 3 рази  більше мастила, ніж у другій , а в третій – на 7л більше, ніж у другій. Скільки літрів мастила було у кожній посудині?

ЗАДАЧА. У першій цистерні було в 1,5 раза більше бензину, ніж у другій. Якщо з першої цистерни вилити 2,5т, а в другу долити 7,5т бензину, то в обох цистернах бензину стане порівну. Скільки бензину було в кожній цистерні спочатку?

ЗАДАЧА. Колесо, що має довжину обводу 2м, на деякій відстані обернулося 360 раз. Скільки разів обернеться на тій самій відстані колесо, довжина обводу якого 1,8м?

ЗАДАЧА. Якщо щодня витрачати 4,2т вугілля, то наявних запасів вистачить на 35 днів. На скільки днів вистачить запасів вугілля, якщо щодня витрачати по 2,8т?

ЗАДАЧА. На першому складі було в 3 рази більше вугілля, ніж на другому. З першого складу взяли 20т вугілля, а в другий привезли 20т вугілля, тепер маса вугілля  на другому складі становить 5/7 маси вугілля на першому складі. Скільки тонн вугілля було спочатку на кожному складі?

Функції, їхні властивості та графіки

Кожній людині постійно доводиться мати справу з різними залежностями між величинами. У відповідності з цим вивчення залежностей є основним змістом їх навчання. Щоб переконатися у цьому, досить погортати сторінки підручників з фізики, хімії, технічних чи суспільних дисциплін, науково-популярних журналів та інших видань. Із закінченням навчання не зникає потреба враховувати, розглядати і досліджувати різні залежності. Для будівельників важливою є залежність вартості будівництва від його тривалості, залежність якості виконаних робіт від якості будівельних матеріалів. Для підприємств автомобільного транспорту викликає інтерес залежність витрат палива від якості доріг. Перелік таких прикладів із господарства, побуту, політики тощо можна продовжити.

Починаючи з ХУІІ ст.. вивчення найважливіших типів залежностей стало основним завданням математики. В математику міцно увійшли поняття змінної величини та функції, які стали і залишаються до цього часу потужними засобами моделювання реальних процесів, а тому й одними з головних об’єктів дослідження.

Функціональні залежності

Природа і життя людини формулює

власні закони мовою математики.

            Г.Галілей.

Практично весь курс алгебри та початків математичного аналізу в школі присвячений вивченню функцій та їх властивостей. Адже наше життя складається із різноманітних явищ, які відбуваються у природі. При цьому зміни одних величин призводять до змін інших. Наприклад, при розгляді руху, можна помітити залежність між шляхом та часом, а при підрахунку площі плоских фігур можна побачити залежність, наприклад, площі круга від його радіуса, а при вивченні теплової дії струму – залежність кількості виділеного тепла від величини струму, опору провідника та часу проходження струму.

Характер залежності та степінь зв’язку між залежними величинами може бути різною. Встановлення ж залежності між різними величинами у різних процесах сприяє відкриттю різноманітних законів і є головним завданням природничих та технічних наук. Якщо залежність між змінними величинами є чітко визначеною, то її називають ФУНКЦІОНАЛЬНОЮ.

При  розв’язуванні  багатьох прикладних задач область визначення функції встановлюють, виходячи з фізичного чи геометричного змісту задачі. Наприклад, якщо розглядати залежність площі квадрата від довжини його сторони х, то областю визначення цієї функції буде інтервал (0;+∞), оскільки довжина сторони квадрата може виражатися тільки додатним числом. У такому разі інколи пишуть: у=х², х>0.

Історично першим способом задання функції був спосіб під назвою аналітичний – за допомогою формули. Він виявився настільки зручним, що функцію почали ототожнювати з її аналітичним вираженням. Виникла об’єктивна необхідність звільнити поняття функції від тісних для неї рамок формули.

Це «звільнення» відбулось у першій половині вісімнадцятого сторіччя. Адже для задання функції необхідно знати дві множини чисел (значення аргументу і значення функції) та закон відповідності між ними. При цьому спосіб встановлення відповідності (спосіб задання функції) принципового значення не має і ніякого впливу на функціональну залежність не встановлює.

Функціональну залежність можна встановити чотирма способами: таблицею, аналітично (формулою), графічно та словесно. Переваги табличного способу полягають у легкості знаходження значень функції відповідно до значень аргументу. За таблицею можна знайти значення функції без будь – яких вимірів та обчислень. Але таблиця не розкриває характер зміни функції в залежності від значень аргументу. Крім того, відсутня і необхідна наочність. Переваги аналітичного способу: компактність задання, можливість підрахунку значень У для будь – якого значення Х, можливість застосування апарату математичного аналізу для дослідження. Недоліком є можлива складність обчислення, недостатня наочність.

Функції, які задаються аналітично, можуть бути зображені і графічно. Але до графіка, як і до таблиці, неможливо застосувати апарат математичного аналізу. Перевага ж графічного способу задання функції  у порівнянні з іншими способами - це наочність. По графіку легко можна дізнатись про «поведінку» даної функції.

Функція також може задаватись і словесно, тобто описово.

Розглянемо приклад задачі на перехід від опису ситуації до формули.

ЗАДАЧА .Складіть формулу функції, яка виражає залежність платні за користування телефоном від тривалості розмов, якщо абонплата складає 5 грн., вартість 1 хв. розмов –2 коп. Врахувати, що 100 хв, надаються безкоштовно, а ПДВ становить 20%.

Перш за все (на етапі аналізу), потрібно з’ясувати, що є аргументом, а що – функцією. У даному випадку х – це час розмов (кількість хвилин), а у – сума до сплати (у гривнях). Далі необхідно встановити область визначення і множину значень: 0 х , 5 у , причому аргумент може набувати лише цілих значень. Спочатку доцільно розглянути простішу задачу – скласти формулу для даної залежності без урахування безкоштовних хвилин та ПДВ. Неважко з’ясувати, що в даному разі формула матиме вигляд у = 5 + 0,02х. Якщо за перші 100 хв, плата не береться, то при 0 х 100 значення функції стале і дорівнює абонплаті, тобто у = 5. Якщо абонент розмовляв більше ніж 100 хв.  (х 100), то з нього беруть додаткову плату за (х – 100) хв, яка становитиме 0,02(х – 100) грн. Отже,

у =

Нарешті, врахуємо ще й ПДВ, який складає 20%. Зробивши необхідні обчислення, матимемо остаточно

у =

Варто переконатись, що знайдено дійсно правильну формулу. Для цього можна надати аргументу конкретного значення (більшого за 100) і обчислити для нього суму до сплати.

У математиці та її застосуваннях дуже поширений графічний спосіб задання функції. Існує багато самописних приладів, які викреслюють криві, встановлюючи тим самим залежність між досліджуваними величинами. Так, сейсмограф записує графік коливання земної кори. За цим графіком можна, наприклад, вивчити силу і характер поштовхів при землетрусі.

За допомогою графіка можна для кожного моменту часу 0≤t≤12 вказати єдине значення температури середовища Т, тобто даний графік буде задавати функціональну залежність між змінними  t і Т. Також, можна графічно показати залежність N(t) кількості деталей, які виготовив робітник, від часу , де t у днях.

  Розглянемо досить нетипові задачі, які можна запропонувати учням для розвитку інтересу до предмета, а також для демонстрації практичного застосування знань з математики. Це задачі, в яких потрібно: задати графічно залежність між деякими величинами, яка задана описово, або для функції, заданої графічно чи аналітично підібрати реальну залежність, або функцію, задану графіком чи таблицею.

  ЗАДАЧА. До кімнати з морозу занесли посудину з льодом. Що з ним буде відбуватися? Побудуйте графік залежності температури речовини від часу.

  ЗАДАЧА. Бензобак автомашини наповнили бензином, який витратили під час кількох поїздок. Побудуйте графік залежності об’єму бензину у бензобаку від часу.

  ЗАДАЧА. Побудуйте графік залежності висоти над землею кабінки атракціону «Оглядове колесо» від часу.

  Головне при розв’язуванні задач даного типу – зобразити динаміку описаного процесу. Розпочати розв’язування задач цього типу, як і задач на перехід від опису до формули, доцільно із визначення незалежної змінної та функції. У першому прикладі – це час і температура речовини відповідно. Функція визначена на множині невід’ємних чисел (х 0), а значень може набувати від температури льоду до температури у кімнаті. На основі певних знань та досвіду про характер залежності можна сказати, що вона не спадна: температура льоду плавно підвищується до 0, а потім деякий час - поки лід не розстане – залишається сталою, після чого температура (тепер уже води) знову зростає. Коли вона досягне кімнатної, процес знову набуде сталості. Але для побудови графіка цього ще недостатньо. Виникає запитання: який вигляд має лінія на проміжках зростання – чи вона пряма, чи опукла, чи увігнута?

      ЗАДАЧА. З’ясуйте, який із графіків відповідає описаній ситуації:

- на газоні росте трава, яку регулярно викошують ( x - час, y – висота трави),

- груша росте, потім її зривають і висушують (x - час, y – маса груші),

- м’яч падає з деякої висоти на підлогу (x – час, y – висота м’яча над підлогою).

                    

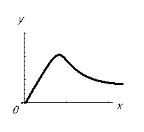
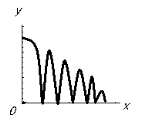
Крім аналітичного і графічного способів задання функцій, застосовується також табличний спосіб. У фізиці і техніці часто залежності між змінними фіксуються на шкалах вимірювальних приладів.

Функціональні залежності широко використовуються на практиці. Наприклад, при рівномірному русі пройдений шлях прямо пропорційний часу, тиск газу р при сталому об’ємі прямо пропорційний його температурі Т: р=сТ (закон Шарля); напруга U в електричному колі зі сталим опором R  прямо пропорційна силі струму I:U=RI (закон Ома). Залежність сили F , яка діє на пружину, від величини її розтягування має вигляд: F=-kx  (закон Гука).

ЗАДАЧА. Маса порожньої бочки 40кг, а маса 1л бензину 0,8кг. Виразіть формулою залежність маси т бочки з бензином від об’єму V бензину в ній. Чи є ця залежність лінійною функцією?

ЗАДАЧА. Щоб пошити одну сорочку , потрібно 2,5м тканини. Запишіть формулу для обчислення залишку тканини після пошиття х сорочок, якщо в сувої 200м тканини. Яких значень може набувати х?

ЗАДАЧА. Учениця дуже полюбляє їсти смажену картоплю. З уроків біології вона знає, що вуглеводи – це гарне джерело енергії. Одного разу їй стало цікаво: скільки енергії вона отримає, якщо з’їсть х грамів смаженої картоплі. При цьому вона знає, що при розчепленні 1г вуглеводів виділяється 17,6кДж енергії. Також дівчину зацікавило: яку кількість калорій вона отримає, знаючи, що у 1г смаженої картоплі 1,92ккал?

ЗАДАЧА. Повернувшись із училища, хлопець пішов на кухню варити пельмені. Набравши у каструлю 1кг води, він ставить її на плиту і чекає, поки вона закипить.

1. Яку кількість теплоти отримає вода при нагріванні до 100⁰, якщо початкова температура води була 20⁰? (Питома ємність води С=4200Дж/кг ^.К. Теплотою, яка припадає на нагрівання каструлі і навколишнього середовища знехтуйте)
2.     Яку кількість газу потрібно використати для передачі такої теплоти? (Питома теплота згоряння газу q=35,5 ^.10⁶. Теплотою, яка припадає на нагрівання каструлі і навколишнього середовища, знехтуйте).

ЗАДАЧА. Висота даху дорівнює 3м, а довжина крокви до її кріплення на 1м більша за половину ширини будинку. Знайти ширину будинку.

ЗАДАЧА. Дві бригади працюючи разом, закінчили ремонт квартири за 6 днів. Скільки днів потрібно було б кожній бригаді на виконання цієї роботи, коли одній для цього потрібно на 5 днів більше, ніж другій?

ЗАДАЧА. Один штукатур може виконати завдання на 5 годин швидше від другого. Обидва разом виконають це завдання за 6 годин. За скільки годин кожен із них виконає завдання?

ЗАДАЧА. Вартість ксерокса після t років використання задається формулою B(t)=8940-745t (грн). Вкажіть :

1. яку функцію задає ця формула;
2. що означає і чому дорівнює В(5);
3. значення t, якщо  B(t)=4470, і поясніть, на що це вказує;
4. початкову вартість ксерокса.

ЗАДАЧА. При вільному падінні тіла з початковою швидкістю v₀= 10м/с залежність пройденого шляху від часу виражається формулою : , де s –шлях,м;  t  - час, с;g≈10м/с² – прискорення вільного падіння. Який шлях пройде тіло за перші 2с? За який час тіло пройде 15м?

ЗАДАЧА. Деяка маса газу при температурі 20⁰С мала об’єм 107см³, а при 40⁰С об’єм дорівнював 114см³. Виходячи із закону Гей - Люссака , знайти функціональну залежність об’єму  газу від температури. Яким буде об’єм газу при 0⁰С?

ЗАДАЧА. Напруга в електричному колі рівномірно зростає, тобто лінійно залежна від часу. На початку досліду напруга дорівнювала 10В, а наприкінці досліду, що тривав 5с, напруга збільшилася у 1,5 разів. Виразіть залежність напруги від часу і побудуйте графік цієї функції. Якою була напруга через 3с після початку досліду?

ЗАДАЧА. Згідно з законом Бойля-Маріотта  , тиск р і об’єм газу V пов’язані формулою , де с – деяке число, стале для даної маси і температури газу. Побудуйте графік цієї залежності, якщо при тиску р=10Па об’єм газу дорівнює 0,5л.

ЗАДАЧА. Опір R провідника визначається за формулою , де l і S – відповідно довжина і площа поперечного перерізу провідника, а ρ – питомий опір речовини, з якої виготовлено провідник. Запишіть залежність:а)S від R;б) l від R. Який графік має кожна з цих функцій?

ЗАДАЧА. Відповідність між довжиною маятника l і його періодом коливання Т задається формулою Т=, де π ≈3,14, g≈9,8м/с². Яку функцію задає ця залежність? Якою функцією задається  залежність довжини маятника від періоду його коливання?

Вивчення розділу „Елементарні функції” дає можливість підвести учнів до усвідомлення того, що кожна функція математично формулює залежності між реальними величинами різних явищ, при чому сама функція застосовується для опису явищ і процесів.

1. Функція  y = k x :

1. залежність між шляхом s, пройденим тілом при сталій швидкості v і часом t його руху:  s = vt ;
2. між вартістю p купленого товару, його кількістю k і сталою ціною t : p = k t;
3. між довжиною кола C і його діаметром d : С =  d;
4. між потужністю струму P і його силою I при сталій напрузі U :        P = I U;
5. закон Ома: U =R I;
6. рівняння конденсатора: q=CU;
7. залежність тиску ідеального газу від кінетичної енергії руху молекул: p=;
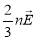8. залежність кінетичної енергії молекул від температури: ;
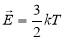9. залежність маси від кількості речовин :  m=Mv.

2.Функція y=ax²:

1) закон вільного падіння тіла: S =;

2) залежність між шляхом S  при рівноприскореному русі від t ,  коли v₀ =0: ;

3) залежність кількості тепла Q , що виділяється струмом за певний проміжок часу, від сили струму I,  опору провідника R , часу проходження струму t : Q=I²Rt.

Чимало фізичних залежностей виражається за допомогою квадратичної функції. Наприклад, закон руху тіла вздовж координатної прямої під дією сталої сили можна подати у вигляді: , залежність кінетичної енергії тіла W , маса якого дорівнює т , від швидкості v виражається формулою : . Тіла які кинули горизонтально чи під кутом до горизонту, рухатимуться по параболічній траєкторії під дією сили тяжіння.

Неважко помітити, що парабола має вісь симетрії. Якщо обертати параболу навколо цієї осі, то вийде поверхня, яка відіграє основну роль у фарах, рефлекторах, антенах радіотелескопів. Річ у тім, що промені світла, які виходять з особливої точки параболи – її фокуса, відзеркалюючись від неї, далі рухаються променями, паралельними осі параболи. І навпаки, - потік паралельних променів, які йдуть, наприклад, від далекої планети чи зорі, збирається у фокусі після відзеркалення від такої поверхні.

Точнісінько такої форми набирає рідина в циліндричній посудині, якщо цю посудину обертати навколо її осі.

                         Вовки – теж параболи

 

 

 

 

 

 

Метро в Чехії

3. Функція у=ах²+вх+с:

1) залежність між шляхом s при рівноприскореному русі від часу t : ;

2) висота h , на якій кинуте вертикально вгору тіло буде знаходитися через час t , де v₀ – початкова швидкість, g - прискорення вільного падіння: .

4. Пряма пропорційність:

1) ізохорний процес: ;

2) ізобарний процес: ;

3) теплове розширення тіл   – лінійна функція ;

4) залежність питомого електричного опору металів від температури - лінійна функція .

5. Обернена пропорційність:

1) ізотермічний процес: ;

2) рух рідини по трубах: ;

3) формула для обчислення відстані до зірки, де – її паралакс у кутових секундах: .

Обернено пропорційними є:

• залежність часу, який витрачається на подолання даного шляху від швидкості;
• залежність між сторонами прямокутника при заданій площі;
• залежність між тиском газу та його об’ємом при сталій температурі.

У біології можна знайти багато прикладів обернено пропорційних залежностей: чисельність особин певного виду на якійсь території і кількість корму; розміри тварин та їх рухливість; розміри тварин та їх плодючість (маленькі тварини дають більше потомства, ніж великі); діаметр кровоносних судин і тиск крові (зі звужуванням судин тиск крові збільшується).

В економіці прикладом оберненої пропорційності є закон попиту: якщо ціна якогось товару підвищується і при цьому  решта умов залишаються незмінними, то попит на цей товар зменшується, тобто кількість проданого товару зменшується.

Основні властивості функції

Вивчення реальних процесів часто зводиться до дослідження залежностей, які описують ці процеси. Дослідити функціональну залежність  - означає виявити її характерні особливості. Характерними особливостями функції є – її зростання чи спадання , парність чи непарність, неперервність.

Зростаючі функції описують процеси  і явища , в яких незалежна величина збільшується зі зростанням незалежної. Наприклад, температура води з часом збільшується при її нагріванні до моменту кипіння. Також збільшується з часом швидкість тіла при вільному падінні до моменту падіння.

Процеси і явища, в яких залежна величина зменшується при зростанні незалежної, описуються спадними функціями. Наприклад, зменшується атмосферний тиск при зростанні висоти над рівнем моря, швидкість тіла при гальмуванні.

Неперервна функція описує процеси , які відбуваються плавно, без «стрибків», тобто коли досліджувана величина за малий проміжок часу змінюється мало. Саме так у звичайних умовах змінюється довжина шляху, пройденого тілом, швидкість механічного руху, температура тіла при охолодженні.

Однак існують процеси, в яких досліджувана величина змінюється стрибками. Наприклад, так змінюється залежно від часу маса товару т , що залишається в машині, якщо його розвантажують ящиками; сума грошей на банківському рахунку залежно від часу, якщо цей рахунок поповнюється, але гроші з цього рахунку не знімаються; висота трави на газоні залежно від часу за умови регулярного її підстригання за допомогою газонокосарки.

Степенева функція

Багато залежностей між величинами описуються за допомогою степеневих функцій з натуральними показниками. Наприклад, об’єм куба V є степеневою функцією від довжини його ребра а:  V=a³; об’єм кулі V є кубічною функцією її радіуса R: .

ЗАДАЧА. Вкладник поклав на свій рахунок до банку 1000грн. Банк нараховує щорічно за схемою складних відсотків р%. Знайти залежність розміру внеску через три роки S₃ від р.

ЗАДАЧА. Потік рідини через поперечний переріз труби обчислюється за формулою: , де Q – потік, R- радіус труби, l – довжина труби, р₁-р₂ – різниця тисків на кінцях труби, η – в’язкість рідини. Виразіть радіус труби через інші змінні.

За допомогою степеневих функцій описують різні процеси і явища. У деяких випадках показник степеня α не є цілим числом. Наприклад, період Т коливання математичного маятника є пропорційним довжині маятника l у степені , а саме: 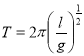, де g – прискорення вільного падіння. Якщо газ розширюється або стискається без теплообміну із навколишнім середовищем, то його тиск Р і об’єм  V пов’язані формулою: , де С – деяка стала. Зокрема , для повітря ця формула набуває вигляду:. Тому корисно знати властивості  степеневих функцій у=х^α  , коли показник степеня α не є цілим числом.

ЗАДАЧА. Населення міста нараховує 225 тисяч мешканців і зростає щорічно на 3% у порівнянні із попереднім роком. Яким стане населення міста через 5 років?

ЗАДАЧА. Швидкість проникнення води у ґрунт  обчислюється за допомогою експериментально встановленої формули: , де v – швидкість проникнення води у ґрунт , мм/год; t – час, год. Знайти значення v при t = 0,1; 0,2; 0,5; 1,0; 2,0; 5,0.

ЗАДАЧА. Залежність максимальної інтенсивності опадів від їхньої тривалості в деякій місцевості описана за допомогою формули : , де І – максимальна інтенсивність опадів, мм/год; t -  тривалість опадів, год. Знайти:

1. максимальну інтенсивність опадів при їхній тривалості : 0,5год; 1год; 2год;
2.   при якій тривалості опадів  максимальна інтенсивність дорівнюватиме 3,6мм/год;
3.   при якій тривалості опадів вища максимальна інтенсивність: при 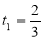год чи при 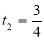год.

ЗАДАЧА. Швидкість різання і стійкість різця пов’язані залежністю: , де V- швидкість різання, м/хв.; Т – стійкість різця (час між двома переточками), хв.

1. Знайти швидкість різання при Т=40хв.
2. Якою буде стійкість різця при швидкості різання 4000м/хв ?
3. Знайдіть залежність стійкості різця від швидкості різання.
4. Чи існує оптимальна швидкість різання, тобто швидкість, для якої стійкість різця найбільша?

ЗАДАЧА. Об’єм куба дорівнює V . Користуючись степенем з дробовим показником, виразіть через об’єм V:

1. довжину ребра куба;
2. площу грані куба;
3. площу поверхні куба.

Приклади функціональних залежностей

Матеріальна єдність світу виявляється у взаємозв’язку і взаємообумовленості різних явищ і процесів, що відбуваються у природі. Розглядаючи їх, доводиться враховувати залежності  одних величин від інших.

Наприклад, залежність довжини шляху від часу, залежність кількості купленого товару на певну суму від ціни, залежність між площею круга і його радіусом.

Необхідність вивчення на практиці залежностей між змінними різної природи привела до поняття функції в математиці.

Залежність довжини шляху S , пройденого тілом, яке рухається рівномірно, від часу t є функцією, що задається формулою , де S₀ – початковий шлях, який пройшло тіло; v – швидкість, яка є сталою при рівномірному русі.

Якщо учні класу, що складається з 25 осіб, чергують протягом січня, крім тих  днів, які припадають на неділю, то кожному з днів січня відповідає певний черговий. Незалежною змінною тут є дні січня, залежною-черговий. Маємо функцію, областю визначення якої є множинна днів січня (без тих, що придають на неділю), а областю зміни - множина учнів класу.

Активна електрична енергія, яка витрачається в колі змінного струму за час   t , є функцією часу і при сталій потужності Р виражається формулою .

  

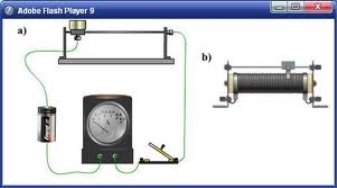
За допомогою графіка функції можна фіксувати протягом кількох років висоту дерева, яке росте.

         

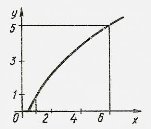
Формула (закон Ома) задає пряму пропорційність (функцію від) при сталому опорі в ланцюгу та змінній напрузі і обернену (функцію від R) - при сталій напрузі та змінному опорі.

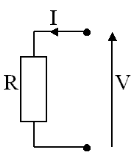
Лінійні функції виражають залежності між змінними різної природи.

                                                  

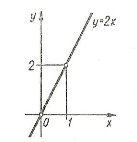
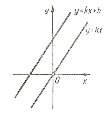
Наприклад:

а) залежність довжини шляху s, який пройде тіло при рівному русі, від часу t визначають за формулою де s- початковий шлях, -стала  швидкість;

б) залежність довжини металевого стержня від температури при нагріванні задають формулою де -довжина стрижня при t=0, k – коефіцієнт лінійного розтягу;

 

в) вартість N телеграми обчислюється за формулою N=5x+20, де х – кількість слів, 5 коп. – вартість одного слова, 20 коп. – попередня оплата;

  

г) вартість проїзду в таксі можна обчислити за формулою Р=20п+20, де п-кількість кілометрів (відстань), що проїхав пасажир, 20 коп. – вартість проїзду одного кілометра, 20 коп. – сума, яка автоматично фіксується на лічильнику, коли пасажир сідає в таксі.

Функції виражають залежність між різними змінними.

  

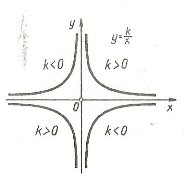
а)  залежність кількості купленого товару на задану суму грошей від ціни товару;

б) залежність сили струму від опору провідника при сталій напрузі (закон Ома);

в) залежність між тиском газу і об’ємом, який він заповнює, (закон Бойля-Маріотта);

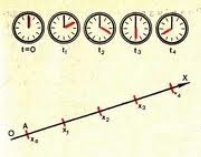
г) залежність часу  від швидкості руху , де s – довжина шляху.

   

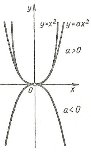
За допомогою функції у=х² виражають залежність площі квадрата від довжини його сторони.

    

На практиці, у фізиці, техніці частіше застосовують функцію у=ах², де а – число.

За допомогою цієї функції виражають, наприклад:

а) залежність площі круга від радіуса S=r²;

б) залежність кінетичної енергії тіла від його швидкості ;

  

в) залежність довжини шляху вільно падаючого тіло від часу (якщо опором середовища нехтувати).

 

Форму параболи у=ах² мають: ланцюг, що підтримує висячий міст за допомогою великої кількості стержнів (якщо масою ланцюга нехтувати);

                

 траєкторія снаряда, що летить;

   

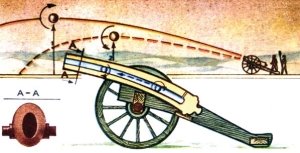
осьовий переріз автомобільної фари;

осьовий переріз вільної поверхні рідини при обертанні посудини з рідною навколо його осі симетрії.

  

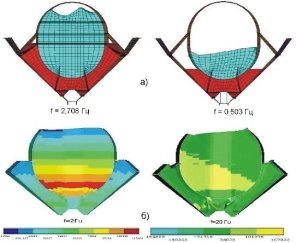
                          Просторові коливання поверхні рідини   при    вібронавантаженні   паливного відсіку

Функція у=x³. Ця функція визначає, наприклад, залежність об’єму куба від довжини його ребра.

Графік у=ах³ використовують проектувальники залізниць та автомобільних шляхів для здійснення плавного переходу від прямо лінійних ділянок шляху до криволінійних.

 

 

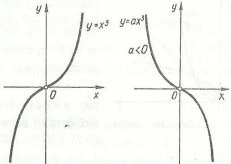
На практиці використовують функцію

 

Зокрема, за допомогою цієї функції вражають залежність періоду Т малих коливань математичного маятника від його довжини l: Т=2, де g – прискорення вільного падіння.

 

 

4.  
5.  
6.  
7.  

ЗАДАЧА. Дано графік залежно швидкості фотосинтезу в певних рослинах від інтенсивності світла. При інтенсивності світла і=1,5од. швидкості фотосинтезу максимальна і дорівнює 202,5 од. Фотосинтез не відбувається, якщо і=3 од. Виведіть формулу даної залежності, вважаючи, що її графік має формулу параболи. При якій інтенсивності світла і швидкість фотосинтезу 112,5 од.? З якою швидкістю відбувається фотосинтез у рослинах при інтенсивності світла і=2?

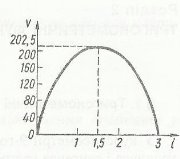
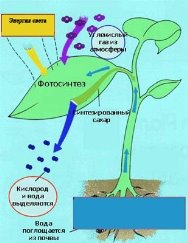
ЗАДАЧА. Використовуючи дані таблиці, побудуйте графік залежності витрати палива в літрах на 100 км шляху автомобілем «Москвич-2141» від його швидкості.

                           

ЗАДАЧА.Опір сухої горизонтальної дороги з твердим покриттям  руху автомобіля, швидкість якого , виражає формулою Дослідити, як змінюється опір дороги при різній швидкості автомобіля, м/с. При якій швидкості опір буде найменшим?

  

ЗАДАЧА. На рисунку  показано графік переміщення тіла, яке рухається рівноприскорено. Яку швидкість воно буде мати через 3 с, якщо початкова швидкість ?

 

 

 

 

 

      

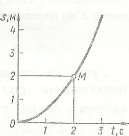
ЗАДАЧА. Для нагрівання води у своїй квартирі господар придбав бойлер на 80л. На початку нагрівання температура води була 16⁰. При нагріванні щогодини температура води підвищувалася на 9⁰.

1. Задати формулою залежність температури  Т води від часу  t її нагрівання.
2. Визначити, при якому значенні t температура води в бойлері стане максимальною.
3. Якою стане температура води в бойлері, якщо господар використав половину гарячої води з бойлера, а її місце заповнила вода температурою 16⁰?

ЗАДАЧА. Для поливу саду господар вирішив виготовити бак для води у вигляді куба з ребром а м і об’ємом V м³.

1. Виразити залежність а від V формулою.
2. Знайти довжину ребра куба, якщо господар планував заливати повний бак 8 м³води.
3.     Скільки десятилітрових відер води потрібно, щоб повністю наповнити бак водою?

У житті ми  зустрічалися  з графіками  на уроках математики, у довідковій літературі, при ознайомленні з графіками зміни температур і руху  потягів. А от і ще приклади.

  1. Сейсмограф

Використовуючи свідчення сейсмографів (приладів тих, що безперервно фіксують коливання грунту і що будують спеціальні графіки - сейсмограми) геологи можуть передбачити наближення землетрусу або цунамі.

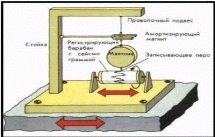Прилад, що демонструє принцип роботи сейсмографа.
        Сучасний сейсмограф Kinemetrics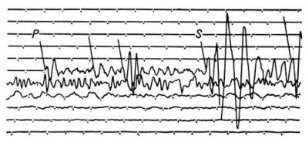
Сейсмограма
           У стародавньому Китаї в період династії Хань часто траплялися землетруси. У народі панував страх з приводу цього таємничого явища природній стихії.Імпе ратор, не знаючи, чим він прогнівав Небесного владику, вирішив підвищити оподаткування по всій країні, щоб зробити багаті жертвопринесення.   В цей час в Китаї жив видатний учений на ім'я Чжан Хен, який займався не тільки астрономією, але і географією, механікою, математикою і сейсмологією. Він вважав, що землетрус – це всього лише одне з природних явищ, яке варто вивчати. Після багаторічних шукань він створив перший в світі своєрідний сейсмограф, який, як свідчать історичні хроніки, досить точно передбачив декілька землетрусів, які відбулися в Лояні - тодішній столиці Піднебесної, а також могутній землетрус в провінції Ганьсу."Дракон, що грається з жабами" або перший в світі сейсмограф.  

2.Медицина 
          Кардіограф. Для вимірювання і реєстрації біоелектричних потенціалів серця при діагностиці стану серцево-судинної системи людини використовують електрокардіографи.

Електрокардіограф здатний зареєструвати різницю електричних потенціалів між двома точками в електричному колі серця під час її порушення. Тобто, при болях у серці, зміні серцебиття, при задишці.

Лікарі виявляють хвороби серця, вивчаючи графіки, отримані за допомогою кардіографа, їх називають кардіограмами.

 

   

Приклади кардіограм

У медицині також використовують прилад спірометр для вимірювання об’єму повітря, яке поступає із легень при найбільшому видиху після найбільшого вдихання.

Застосовується для оцінки стану дихальної системи людини з допомогою вимірювання і обчислення усіх основних параметрів дихання.

Співвідношення цих параметрів показує ступінь порушення бронхіальної прохідності.

          3. Застосування графіків
          Широко застосовуються графіки в економіці, зокрема -  крива попиту і пропозиції, лінія виробничих можливостей та інші:

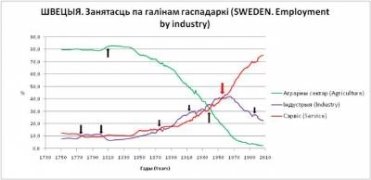
                                  Графіки зайнятості в аграрному секторі   і секторі послуг

          Існує залежність розміру повітряної камери яйця від термінів зберігання , температури і вологості навколишнього повітря. Це є показником свіжості яєць.

На графіках зображено залежність зміни РН білка і жовтка від часу інкубаційного періоду.

В свіжих яйцях білок має лужну реакцію, але в процесі інкубації РН білка знижується.

Жовток у свіжих яйцях має кислу реакцію, але в процесі інкубації ПР жовтка зростає, що пов’язано із змінами хімічного складу жовтка у період інкубації

      

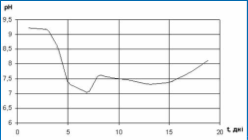
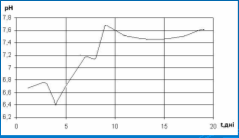
Функціональну залежність можна побачити і у різних видах спорту.

Графічно зображено залежність швидкості руху велосипедиста від опору повітря.Для подолання опору повітря і відповідно, зміни швидкості, велосипедист змінює положення тіла.

Існують функціональні залежності між основними фізичними величинами. Одним із прикладів можна навести явище дисперсії. Тобто, залежність показника заломлення різних речовин від довжини хвилі.

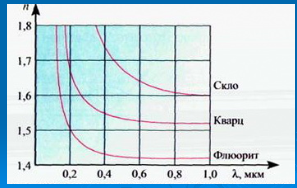
Соціальна сфера – це ще один приклад відображення функціональної залежності.

Не є новиною, що рівень заробітної плати дуже часто залежить від рівня освіченості людини.

Даний графік демонструє залежність річного заробітку працівника від рівня освіти.

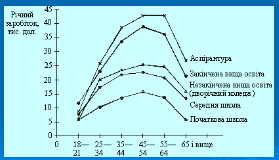
Прилад термограф використовують на метеорологічних станціях для прогнозування погоди. Термограф безперервно реєструє  покази температури води і повітря. Це приклад функціональної залежності температури від часу.

Щоб будь-яка подорож по морю була цікавою, легкою, комфортною, необхідно передбачити можливість виникнення шторму. Її записують за допомогою метеорологічного радіолокатора, який оцінює горизонтальну і вертикальну швидкість опадів. Барограма демонструє функціональну залежність між відстанню і часом.

 

 

 

Тригонометричні функції

Введення тригонометричних функцій було зумовлене потребами астрономії а також будівельної справи, адже саме для розв’язання цих задач стародавні вчені досліджували співвідношення різних величин у трикутнику.

Синус зустрічається в індійських книгах з астрономії IV-V ст. Лінія синуса називалася «ардхаджива», що буквально означає «половина хорди». Пізніше синус почали називати коротше «джива» - хорда. В арабській літературі індійський термін був перероблений в «джиба», а згодом у «джайб», що означає «опуклість»

Слово «синус» є буквальним перекладом арабського «джайб» на латинську.

Слово «косинус» є скороченям виразу «додатковий синус» (точніше , синус додаткового кута). Запропонував цей термін в 1620р. англійський математик і астроном Гентер.

Термін «тангенс», у розумінні тінь вертикальної палиці, був введений арабським математиком Абу-л-Вафою в Х ст. Цей результат залишився невідомим у Європі, і тангенс заново відкрив спочатку Брадвардин (ХІVст.), а згодом Регіомонтан (XVст.) . Латинською мовою тангенс означає – «дотична». Запропонував цей термін Фінке (1583р.). 

Тригонометрія має велике практичне значення, зокрема, для розв’язання задач на знаходження площ і об’ємів, на додавання і розкладання сил, на знаходження віддалей до недоступних предметів тощо.

Першим графіком тригонометричної функції, що з’явився в друкованих публікаціях, була синусоїда, розміщена в одному з творів французького математика Жиля Персона де Роберваля. Цей графік був накреслений в кінці 30-х років 17ст. Подальший розвиток тригонометрії тісно пов’язаний з іменем Леонарда Ейлера.

Доведено, що будь-яке періодичне коливання можна зобразити як суму синусоїдальних коливань.

З історії математики відомо, що виникнення тригонометрії пов’язане з вимірюванням довжин і кутів. Проте , сфера її застосування є набагато ширшою, ніж у давнину.

В давнину за допомогою тригонометрії люди навчилися вимірювати уявні трикутники на небі, вершинами яких були зірки. Зараз тригонометрію застосовують навіть для вимірювання відстані між космічними кораблями.

Тригонометричні обчислення застосовуються практично у всіх областях геометрії, фізики й інженерної справи. Велике значення має техніка тріангуляції, що дозволяє вимірювати відстані до недалеких зірок в астрономії, між орієнтирами в географії, контролювати системи навігації супутників. Також слід відзначити застосування тригонометрії в таких областях, як теорія музики, акустика, оптика, аналіз фінансових ринків, електроніка, теорія ймовірностей, статистика, біологія, медицина (включаючи ультразвукове дослідження (УЗД) і комп'ютерну томографію), фармацевтика, хімія, теорія чисел (і, як наслідок, криптографія), сейсмологія, метеорологія, океанологія, картографія, фізика, топографія та геодезія, архітектура, фонетика, економіка, електронна техніка, машинобудування, комп'ютерна графіка, кристалографія.

Тригонометричні функції застосовують для характеристики періодичних процесів. Більшість застосувань тригонометрії стосується саме періодичних процесів, тобто процесів, які через рівні проміжки часу повторюються. У природі зустрічаються явища, які повторюються періодично. Наприклад, Земля при обертанні навколо Сонця періодично повертається у своє початкове положення через рік, два роки, три роки і т.д., тому говорять, що період обертання Землі навколо Сонця дорівнює одному року. Періодичний характер  мають рухи маховика і колінчатого вала. Властивість періодичності мають звукові , електромагнітні явища, робота серця людини і т.д. Отже,  обертання  колеса , схід і захід Сонця, зміни пір року ,– це найпростіші приклади закономірності періодичних явищ.

Що спільного між рухом Сонця і функцією синуса?

 

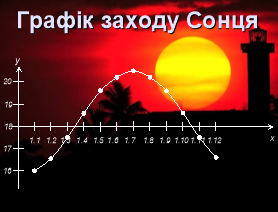
Досить часто у технічних приладах використовують графік функції синус.

Механічні та електромагнітні коливання є також важливими прикладами періодичних процесів. Тому дослідження періодичних процесів є важливим завданням. І роль математики в його розв’язанні є визначальною.

Змінний струм синусоїдальний, тобто сила струму в кожній ділянці ланцюга змінюється по синусоїдальному закону І=І0sin(wt+µ), де

 І0 – амплітуда струму,

 w – циклічна частота,

 µ - початкова фаза.

ЕРС (електрорушійна сила) ланцюга також змінюється по синусоїдальному закону.

Часто положення рухомих об’єктів, наприклад, небесних тіл, визначають за допомогою кутів, зокрема, кутів обертання. Тому функції , що описують їхній рух, нерідко своїм аргументом мають міру кута.

Наприклад, літак із пункту А має перелетіти у пункт В. Курс  літака визначають за допомогою кута між напрямом лінії польоту і напрямом меридіана «південь-північ», який відлічують проти годинникової стрілки. При русі літака потрібно стежити, щоб частота синусоїдних коливань літака, спричинена роботою мотора,  не збігались з частотою якою-небудь деталі літака.  Резонанс синусоїдних  коливань літака може призвести до аварії.

Рух точки по колу багато у чому схожий з рухом точки по прямій. Щоб визначити положення точки на прямій , недостатньо знати шлях, пройдений нею від початкової точки, - потрібно вказати напрям руху. Зазвичай на прямій фіксують додатній напрям, а положення точки визначається одним числом, додатним чи від’ємним.

При обертанні на площині будемо вважати додатним напрямом обертання проти руху годинникової стрілки.

Введення радіанної міри кута обертання дає змогу встановити простий зв'язок між кутовою і лінійною швидкостями точки, яка перебуває у рівномірному обертальному русі. Кутова швидкість при рівномірному обертанні  - це кут, на який повертається точка за одиницю часу. Вона зазвичай вимірюється в радіанах за секунду (рад/с). Лінійна швидкість точки при  рівномірному русі – це відстань ,на яку  переміщується точка по траєкторії руху за одиницю часу.

ЗАДАЧА. Точка рівномірно рухається по колу, радіус якого R=40см, з лінійною швидкістю ν=80см/с. Знайти кутову швидкість точки.

В географії, астрономії, де застосовується градусна система вимірювання кутів, послуговуються також меншими одиницями вимірювання: (кутова мінута), (кутова секунда). Градусною мірою кута послуговуються в оптичних приладах.

 

 

У техніці за одиницю вимірювання кутів приймають повний оберт, у військовій справі – «тисячну», тобто частину розгорнутого кута , чи

велику поділку кутоміра, яка дорівнює 100 «тисячним». У мореплавстві одиницею вимірювання є румб, що дорівнює  частині повного оберту.

ЗАДАЧА. Чому дорівнює у градусній мірі кут обертання маховика, що зробив за годинниковою стрілкою : 1 оберт; 1,5 оберту?

Існує відповідність між дійсними числами і точками одиничного кола (використовується вимірювання відстані вздовж кола). Різним числам може відповідати та сама точка тригонометричного кола.

Це неоднозначно нагадує таку реальну ситуацію: велотрек має довжину 350м, велосипедист знаходиться  на відстані 150м від фінішу. Який шлях він проїхав?

ЗАДАЧА. Зубчасте колесо має 40 зубців. Виразіть у градусах кут, на який обернеться колесо при повороті на 1 зубець; 15 зубців; 80 зубців; 150 зубців.

ЗАДАЧА.  Колесо за 10с повернулося на 5π рад. З якою кутовою швидкістю воно обертається?

ЗАДАЧА. Колесо автомобіля за 2с робить 6 обертів. Запишіть у градусах кут, на який повертається колесо за 1с; 5с.

ЗАДАЧА. Велосипедист підрахував, що колесо його велосипеда, довжина спиці якого30см, за дві секунди робить 6 обертів.

1. Знайти у градусах кут, на який повернеться колесо велосипеда за 1 секунду.
2. Подати цей кут у радіанах.
3. Скільки обертів зробить колесо, якщо велосипедист проїде 18,84м?

ЗАДАЧА. Шків швидкісного електродвигуна робить 90000 обертів за хвилину. Знайдіть кутову швидкість обертання цього шківа : 1) у град/с; 2) у рад/с.

ЗАДАЧА. Точка рухається рівномірно по колу радіуса R = 60см з кутовою швидкістю ω=4π рад/с. Знайдіть її лінійну швидкість.

ЗАДАЧА. Точка рухається рівномірно по колу радіуса R = 30см  з лінійною швидкістю 75см/с. Знайдіть її кутову швидкість.

ЗАДАЧА. Яку лінійну швидкість має точка диска, що обертається, коли вона віддалена на 18см від осі обертання, а кутова швидкість диска дорівнює   рад/с? Якої довжини дугу опише ця точка за 45с?

ЗАДАЧА. Кліть шахтного підйомника піднімається на 100м за 40 повних обертів вала підйомника у додатному напрямі. Визначте у радіанах кут повороту вала підйомника, якщо кліть піднялася на 13,75м; спустилася на 21м.

ЗАДАЧА. Дрібне вугілля насипане у купу, що має форму конуса, причому кут при основі конуса α=50⁰. Знайти коефіцієнт тертя вугілля.

У шахті вимірюють кути спеціальними приладами тахеометрами.

 

 

 

 

За допомогою тригонометричних функцій електрослюсар підземний визначає коефіцієнт потужності електроустановок.

 

 

Підвищення   електробезпеки можливе за допомогою схеми управління короткими замиканнями ЕРС двигуна.

А така формула з використанням тригонометричних функцій дає змогу розраховувати струм короткого замикання

       .

За допомогою тригонометричних формул можна передбачити зсув ґрунту, а отже і трагедію в шахті.

Активна потужність двигуна вугільного комбайна така: . Чим більший   , тим менше втрата електроенергії.
            В залежності від кута нахилу гірничої виробки використовують різні типи стрічкових і скребкових конвеєрів.

Тригонометричні функції розглядаються як функції числового аргументу. Введення радіанного вимірювання кутів приводить до того, що кожному дійсному числу  можна поставити у відповідність певний кут в  радіан і, навпаки, кожному куту – дійсне число, величина якого  радіан. В теоретичних дослідженнях і в практиці переважно використовують радіанну систему вимірювання кутів і дуг, при якій кут і дуга, що йому відповідає, виражаються відношенням довжини дуги даного центрального кута до її радіусу. Так як відношення довжини дуги до довжини свого радіуса є постійною величиною для даного кута і може служити мірою цього кута. За значенням цієї величини можна твердити про величину даного кута.

В різних прикладних задачах аргументом тригонометричних функцій можуть бути не лише кути і дуги, але і інші геометричні і фізичні величини: довжина, час, температура і т.д.

ЗАДАЧА. У вузлі електричного коло сума вихідних струмів дорівнює сумі вхідних. Якщо струми змінні, то це твердження справедливе для миттєвих значень сил струму, тобто, необхідно при додаванні струмів врахувати їх частоти і фази. Таке додавання можна здійснити, використавши формули додавання тригонометричних функцій.

ЗАДАЧА. При переході світлового променю із одного середовища в інше відбувається заломлення, тобто відхилення від початкового напрямку. Коефіцієнт заломлення дорівнює відношенню =n , де  - кут падіння променю на межу середовищ;  ^/- кут відхилення.

ЗАДАЧА, При конструюванні оптичних приладів доводиться розв’язувати задачі , подібні до наступних:

•                   Як потрібно направити промінь на межу двох середовищ, щоб кут падіння променю був більший за кут заломлення на дану величину?
•                   Якщо коефіцієнт заломлення дорівнює п, а кут падіння більший за кут заломлення на , то знаходження шуканого кута падіння х зводиться до рівняння 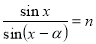, яке не можна розв’язати без знання теорем додавання.

При вивченні матеріалу про властивості тригонометричних функцій і побудови їх графіків використовують властивості графіків парних і непарних функцій: симетричність відносно осі, центру; геометричні перетворення графіків: стиск і розтяг, паралельне перенесення.

Багато фізичних величин періодично змінюються  і можуть бути описані за допомогою тригонометричних функцій      у=А sin(kx+a) або y=A cos (kx+a);   де A, k, a- задані числа,А≠0, k≠0. У такому випадку говорять, що фізична величина здійснює гармонічне коливання а функцію називають функцією гармонічного коливання.

В природі часто зустрічаємося з явищами, які повторюються періодично. Наприклад, Земля при обертанні навколо Сонця періодично повертається у своє положення через рік, два роки, три роки і т.д., тому говорять, що період обертання Землі кругом Сонця дорівнює одному року. Період обертання по орбіті комети Галлея дорівнює 76 рокам.

Звучання струни, рух маятника, морські припливи, найрізноманітніші біоритми живих організмів, рух тіла по колу, голки  швейної машинки, коливання гілки дерева на вітрі – все це  лише окремі приклади у нескінченній множині коливних  або періодичних явищ. А щоб описати їх, поставити на службу, людям треба побудувати  математичні моделі таких явищ. Математичний опис періодичних процесів створювали вже вчені стародавнього світу. Так,  вавилонські астрономи деякі  закономірності руху Місяця і Сонця виразили у вигляді спеціальних таблиць, які вони назвали функціями. Теорія тригонометричних функцій  теж є однією з найдавніших моделей періодичних явищ.

Людина  зустрічається   з коливаннями і використовує їх у різних сферах своєї діяльності: періодичний характер деяких процесів  у людському організмі, біоритмологія  , біологічний годинник, звуки та слух, фізичні основи будови голосового апарата людини та тварин, звукові методи дослідження в клініці.

Періодичний характер має рух маховика колінчатого валу. Властивістю періодичності володіють багато звукових і електромагнітних явищ, робота серця людини і т. д.

Закономірності періодичних явищ записуються  у вигляді функцій. Досліджуючи ці функції, розкривають внутрішній зміст таких явищ і вказують шляхи їх практичного застосування.

Практичне застосування.

1. Застосування формул тригонометрії та тотожних перетворень тригонометричних виразів для виконання виробничих операцій.

2. Розрахунок кутової швидкості при обробці деревини (різьбярі).

3. Застосування графіків тригонометричних функцій змінного струму в колі (електрослюсарі).

4. З кривими, що мають форму синусоїди, мають справи бляхарі при з’єднані двох циліндричних труб під деяким кутом. Якщо поверхню однієї з таких труб розрізати по її твірній і потім розгорнути на площині, то зроблений косий зріз дає дугу синусоїди.

5. Аналогічно створює викройку кравець, де потрібно вшити рукав у пройму.

6. Упруга пластинка під впливом стиску  вгинається по синусоїді.

ЗАДАЧА. Побудуйте графік залежності моментів заходу Сонця на перше число місяця в залежності від місяця , взявши за вісь абсцис середній час заходу Сонця – 18годин , з’єднайте отримані точки плавною неперервною лінією (ці дані можна взяти з відривних календарів за різні роки або знайти в Інтернеті).

1). Чи є ця залежність функціональною?

2). Графік якої функції нагадує вам побудований графік?

3) Чим ви пояснює таку схожість?

4) Як можна уточнити побудований графік?

5) Чим ви пояснюєте відмінності побудованого графіка від графіка відомої вам функції?

6) Надайте змістовну інтерпретацію області визначення, множині значень, проміжкам монотонності, нулям, найбільшому і найменшому значенням, точкам екстремуму, періодичності функції, графік якої побудовано.

ЗАДАЧА. Дано закон, за яким змінюється з часом сила змінного струму: I(t)=5sin10πt, I-сила струму,A;  t – час, с.

1. Знайдіть амплітуду, період, кругову частоту коливань сили струму.
2. Чому дорівнює сила струму в момент часу t=0,05с?
3. В які моменти часу сила струму набуває найбільшого значення?

ЗАДАЧА. Дано закон, за яким змінюється з часом напруга : U(t)=220cos60πt, U- напруга, B;  t – час, с.

1. Знайдіть амплітуду, період, частоту коливань напруги.
2. Чому дорівнює напруга у момент часу  t = 0,5с?
3. В які моменти часу напруга набуває найбільшого значення?

Властивості і графіки тригонометричних функцій

Тригонометричні функції – періодичні. Періодичні функції описують різні ситуації (астрономічні явища, життєдіяльність організму тощо), які періодично повторюються. Періодичними функціями описуються також гармонічні коливання.

Періодичними функціями описуються різні фізичні процеси: малі коливання маятника, обертання планет навколо Сонця, сила змінного струму. Найпростішим прикладом для ілюстрації періодичних процесів є годинник. Положення кінців стрілок повторюються через рівні проміжки часу. Для секундної стрілки цей проміжок складає 60с, для хвилинної – 60хв, для годинникової – 12год.

Також можна спостерігати хвильові процеси: хвилі на морі, на хлібній ниві, коливання (землетрус) кори нашої планети. І все це відбуваєтсья за законом синусоїди.

У навколишньому середовищі широко розповсюджені коливальні рухи. Уявлення про них дають і океанські хвилі, і маятникові годинники, і гойдалки, і нервові імпульси. З ними пов’язане поширення  звуку і світла. Багато цих явищ можна описати за допомогою гармонічних коливань.

Усюди в нашому житті ми зустрічаємось з коливальними рухами, починаючи від коливань маятника, ресори, струсів кузова автомобіля, чи вагона потяга до страшних, руйнівних коливань кори нашої планети; заводські труби і високі будівлі коливаються від вітру подібно до полотна ножівки, затисненого одним кінцем в лещатах. Правда, ці коливання не такі вже й великі. Амплітуда коливань Ейфелевої вежі у Парижі (300м висота) при сильному вітрі приблизно 50см.

При русі літака потрібно стежити, щоб частота синусоїдних коливань літака, спричинена роботою мотора,  не збігались з частотою якою-небудь деталі літака. Резонанс синусоїдних коливань літака може призвести до аварії.

Розглядаючи графіки тригонометричних функцій,можна згадати,що в повсякденному житті ми бачили схожі криві та поверхні. Наприклад, хвилі на морі мають форму,що нагадує синусоїду.

  

Та чи завжди коливання є корисними?

Вібрації – це коливання твердого тіла навколо положення рівноваги, при цьому або все тіло коливається як єдине ціле, не змінюючи своєї форми, або коливаються частинки, які складають  тіло. В основі вібрації лежить коливальний процес, а хвильовий рух – розповсюдження цих коливань.

Як це впливає на організм людини?

Вібрація станка діє на різець та обробляємо деталь та може привести до браку.

Вібрація рідини в паливних баках ракети загрожує їх цілісності.

Добре затягнута  гайка під дією вібрації послаблюється  та станок розшарується.

Коливання, розповсюджуючись по тілу, викликають в тканинах організму стійкі порушення нормальних фізіологічних функцій – «вібраційну хворобу». Ця хвороба приводить до серйозних порушень в людському організмі : судинні порушення (особливо порушення капілярного кровообігу); функціональні порушення центральної нервової системи, що проявляється в головних болях, порушеннях сну, підвищенні втомлюваності,  кісткові порушення, порушення функцій внутрішніх органів тощо. Багато хто з нас відчували  дію коливань на свій організм під час качки пароплава чи літака.

Зрозуміло, що вібраційна хвороба – це дуже серйозне захворювання .

Люди яких професій можуть захворіти нею?

Вібраційну дію на собі зазнають дуже багато людей різних  спеціальностей: бурильники, слюсарі, шліфувальники,  навіть, провідники залізничного вагону. Механізовані інструменти, які являються джерелами вібрацій, широко застосовуються в різних областях промисловості: гірничій (перфоратори, відбійні молотки горні свердла); лісній (моторні та електричні пилки); машинобудівній (тубільні, клепальні молотки, шліфувальні та полірувальні машини, бетоноломи).

Показникова та логарифмічна функції

Основним  призначенням сучасної математики є моделювання явищ природи і суспільства, причому поняття функції належить до найважливіших засобів моделювання. Тому цілком природною і актуальною є проблема збагачення класів функцій.

У природничих науках і техніці зустрічаються процеси, зростання або «згасання» яких відбувається  швидше, ніж у будь-якої степеневої функції. Такі процеси описуються показниковими функціями. Для опису реальних процесів також широко застосовуються логарифмічні функції.

Нині багато говорять про інформаційний бум. Стверджують, що кількість інформації подвоюється кожні десять років. Зобразимо цей процес у вигляді графіка деякої функції.

Візьмемо обсяг інформації в деякий початковий рік за 1. Удвічі більший відрізок поставимо над одиничною оцінкою, вважаючи, що оцінка відповідає першому десятку років. Удвічі більший відрізок відповідає другому десятку років, ще вдвічі більший – третьому і т.д. Обране нами значення аргументу є елементами арифметичної прогресії: 2, 4, 8, … Сполучимо всі побудовані точки плавною лінією – перед нами графік показникової функції. Головна особливість графіка цієї функції – її крутизна.

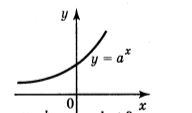
Показникова функція  зустрічається в описі процесів, у яких швидкість зміни величини пропорційна до самої величини. За таким правилом розмножується все живе, збільшується колонія мікробів у чашці Петрі. За таким саме законом плодилися кролі, які за короткий термін заполонили Австралію. Прикладом показникового спадання є хід хімічної реакції: швидкість хімічної реакції пропорційно до кількості речовин, що реагують. Швидкість радіоактивного розпаду також пропорційна до кількості атомів, що не розпалися.

     Зупинемося на радіоактивному розпаді, який описується рівнянням 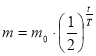, де  m – маса речовини в момент часу t; - маса речовини в момент часу t=0; T – період напіврозпаду.

До показникової функції привело розширене поняття степеня. Показникові функції мають чудову властивість: швидкість їхнього зростання пропорційна  значенню самих функцій. Необхідність їхнього вивчення виникла з дослідження різних законів природознавства, таких, як закони розмноження, біологічних популяцій, закони радіоактивного розпаду, закони руху в гальмуючому середовищі.

За допомогою показникових функцій описують різні процеси і явища. Наприклад , процес розпаду радію можна описати за допомогою формули , де t – час, с, m=m(t) - маса радію в момент часу t, г; m₀=m(0) –початкова маса радію, г; а – деяке дійсне число. Залежність температури тіла Т від часу t при охолодженні його в середовищі зі сталою температурою Т₀ можна виразити за допомогою формули Т=Т₀+(Т₁-Т₀)а^t, де Т₁ – початкова температура тіла. Процеси новоутворення та розпаду можна описати за допомогою формули P=P₀e^kt. Тут Р – кількість новоутвореної речовини (або речовини, що розпалася) в момент часу t ; Р₀ – початкова кількість речовини; k – стала, значення якої визначається для конкретної ситуації.

Формула складних відсотків задає залежність суми А_t на рахунку вкладника банку, який нараховує за кожну одиницю часу р% , від часу t. Необхідність обчислення складних відсотків була викликана зростанням торговельно-фінансових операцій.

За допомогою подібних функцій описують розвиток біологічних популяцій, витрати підприємства, зростання кількості публікацій, обсягу інформації тощо.

ЗАДАЧА. Атмосферний тиск залежно від висоти місцевості  над рівнем моря змінюється за законом р=1,01^.10^5.0,882^h, де р- тиск, Па, h- висота, км.

1). Знайти атмосферний тиск на всіх рівнях – від рівня моря до рівня найвищої земної вершини – з інтервалом в 1км.

2). На якій висоті знаходиться вершина гори, якщо атмосферний тиск на ній дорівнює  5,00 ^.10⁴Па?

ЗАДАЧА. Швидкість занурення тіла в рідину описується формулою , де v - швидкість , м/с;t- час, с.

1). Знайти швидкість тіла через 10с і 20с після початку занурення.

2) На скільки зміниться швидкість за перші 10с занурення? За наступні 10с?

ЗАДАЧА. При радіоактивному розпаді кількість речовин зменшується вдвічі за добу. Скільки речовини залишиться від 250г через 1,5 доби? 3,5 доби? 100 діб?

ЗАДАЧА. Відомо, що коли при радіоактивному розпаді кількість речовини за добу зменшується вдвічі, то через х діб від маси М₀ залишається маса М, яка обчислюється за формулою М=М₀(1/2)^х.

 Звідси   ^х.  Покажіть графічно, як із зміною х змінюється відношення       _.

Використовуючи у випадку необхідності побудований графік, дайте відповіді (точні або наближені) на запитання:

А) У скільки разів зменшиться маса радіоактивної речовини через 1,5 доби, 2,5 доби, 3 доби, 4 доби?

Б)Скільки часу повинно минути, щоб початкова маса радіоактивної речовини зменшилася у 2,5рази, у 3 рази, у 4 рази?

ЗАДАЧА. Коли CD-програвач вимикають, то сила струму в ньому зменшується за формулою I(t)=24^.(0,25)^t (A), де t-сила струму в амперах,  t- час у секундах. Знайдіть:а)силу струму в момент вимкнення CD-програвача;б) I(t), якщо t дорівнює:1с,2с, 3с,4с; в)протягом якого часу сила струму у вимкненому  CD-програвачі перевищує 4А. Скористайтеся графіком залежності  I(t)=24^.(0,25)^t.

Показникова  функція.

Під час вивчення теми „Показникова функція” звертаємо увагу на те, що за допомогою відповідної формули вдалося визначити відстань планет Сонячної системи від Сонця. Справді, відстань від Сонця до Меркурія дорівнює приблизно 0,4 астрономічної одиниці, Венери – 0,7, Землі – 1, Марса – 1,6, Юпітера – 2,8 і т.д. Ця формула допомогла вченим визначити положення трьох найвіддаленіших планет, які в телескоп були малопомітні.

Особливим явищем у науці стало відкриття в  1846 році невідомої до того часу планети Нептун. Її орбіту визначили незалежно один від одного на „кінчику пера ” вчені Адамс і Левар’є. 

Показникова  функція описує: закон радіоактивного розпаду,  зріст народонаселення, барометричну формулу.

  Коли ви познайомитеся з початками математичного аналізу і трохи оволодієте диференціюванням та інтегруванням, то переконаєтесь, що всі розглянуті нами сьогодні різноманітні процеси описуються одним диференціальним рівнянням, яке має назву рівняння показникового зростання   і показникового спадання. 

Зупинемося на радіоактивному розпаді, який описується рівнянням 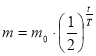, де  m – маса речовини в момент часу t; - маса речовини в момент часу t=0; T – період напіврозпаду.

ЗАДАЧА. Обчислити, яка частина радія залишиться через 1000 років, якщо період його піврозпаду дорівнює 1550 років.

          Для струму для парашутиста для охолодження тіла   Т^І = - k(Т-Т₁),  для демографії S^І (t) = kS(t) тощо.

Спільним для всіх цих процесів є те, що в них швидкість зміни функції (тобто її похідна) пропорційна цій функціїї.

Той факт, що найрізноманітніші явища описуються однаковим диференційними рівняннями, використовується на практиці. Він дозволяє вивчати одні явища, спостерігаючи інші, якщо вони описуються однаковими рівняннями. Наприклад, треба з’ясувати, як рухається під землею нафта в районі бурових свердловин. Цей процес спостерігати під землею було б дуже тяжко. Але рух рідини описується тими самими диференційними рівняннями, що й рух електричного струму. Тому збирають відповідне електричне коло, вимірюють напругу і силу струму в різних його точках, щоб дізнатися, де краще поставити бурову вишку, куди накачали воду, щоб посилити вихід нафти тощо.

Таке вивчення одних явищ за допомогою інших, що описується за допомогою тих самих рівнянь, називається моделюванням явищ.

Електричне коло – це фізична модель руху нафти під землею, а диференціальне рівняння f^/ (х)= k f(х) – це математична модель великої низки природних, фізичних, хімічних, біологічних, навіть соціальних процесів. Розв’язком цього рівняння є функція f(х)=Се^kх – славнозвісна експонента, що по праву заслуговує бути оспіваною в одах.          

Показникова функція в океанських глибинах

Зараз у багатьох океанах і морях працюють науково-дослідницькі кораблі. У заздалегідь установлених місцях вони зупиняються і спускають за борт троси, на кінці яких закріплено прилади. Їх опускають на дно, а потім піднімають нагору і записують покази. Але іноді трос розвивається – і всі цінні прилади залишаються на дні океану.

Здавалося б, біди можна було б уникнути, зробивши трос товстішим. Але тут виникає нове ускладнення – верхні частини троса повинні утримувати прилади, а й нижню частину троса, а через це потовщення всього троса на верхню частину ляже більше навантаження. Тому доцільно робити нижню частину троса тоншою, ніж верхня. Виникає питання: як повинна мінятися товщина троса для того, щоб у будь якому його перерізі на 1 см² припадало те саме навантаження?

Дослідження показали, що площа перерізу троса повинна змінюватися за законом

де S₀ - площа нижнього перерізу,

S - площа перерізу на висоті х від нижнього перерізу,

γ - питома вага матеріалу, з якого зроблено трос,

P - вага у воді вантажу, що опускається (у формулі записано не γ, а γ – 1, бо матеріал троса втрачає у воді вагу за законом Архімеда).

Такі ж троси використовуються і в шахтах, для того щоб опускати кліть з робітниками.

  Тільки тут Канат рівного опору на розрив має меншу масу, менший об’єм, на нього йде менше матеріалу.

Показникова функція в демографії

Нехай населення країни зростає на 2% на рік. Тоді якщо S₀ - кількість населення в деякий початковий момент часу, а S(t) - кількість населення через t років, то S(t)=S₀ · 1,02^t.

Показникова функція в лісівництві

Якщо приріст деревини становить p%, а початкова кількість деревини А₀, то   А(t)=А₀ · (1+ p · 1,01)^t.

Якщо p=10%, то за 6 років кількість деревини збільшиться лише в 1,7 раза. Як бачимо, цей процес іде дуже повільно. Тож збереження лісу, цієї головної фабрики кисню, а отже, захист довкілля є актуальною проблемою.

Показникова функція в біології

Розглянемо, як зростає популяція бактерій у відповідності з простим життєвим циклом. При цьому час між моментом поділу материнської клітини (народження нової) і моментом, коли вона сама ділиться, називається періодом поділу, або часом генерації.

Нехай число бактерій у культурі становить А₀. За час однієї генерації всі ці А₀ бактерій поділяються навпіл і утвориться 2А₀ бактерій. Через дві генерації їх стане 2 · 2А₀, через три – 2 · 2 · 2 А₀ і т. д. Через p генерацій   А=2^p · А₀.

  Нехай час однієї генерації Т, тоді де t – час з початку поділу.

Бачимо, що популяція росте за показниковим законом, або, як кажуть, експоненціально (лат. еxponens – той, хто показує). Про логарифмуємо обидві частини рівняння за основою 10.

Саме здатність бактерій до швидкого розмноження забезпечує їх кількісну перевагу серед живих форм. Якби не було природних причин, що заважали б вибухам кількості бактерій, сумарна маса яких становила б декілька десятків тисяч тонн, а за дві доби показникового зростання маса однієї бактерії перевищила б у декілька разів масу Земної кулі. Наша планета, проте, не перетворилася на суцільну масу мікробів. І це не тільки тому, що бактерії вичерпують поживні речовини, які підтримують їх зростання, а й тому, що при зростанні вони виділяють велику кількість продуктів, токсичних для них самих.

З відкриттям англійським мікробіологом Флемінгом пеніциліну і народженням нової промисловості знати кількість грибків, утворених у процесі розвитку, стало важливо і можливо при використанні виведеної раніше формули.

ЗАДАЧА. Ентомолог, визначаючи нашестя саранчі, дослідив, що площа (у м²), заражена саранчею,змінюється за формулою S_n=1000^.2^0,2n,де n – кількість тижнів після зараження. Знайдіть:

1. початкову площу зараження,

2. яку площу заражено через 5 тижнів,

3. яку площу заражено через 10 тижнів.

ЗАДАЧА. Під час вирощування бактерій маса культури змінюється за формулою (г), де t – час у годинах, пройдений після початку розмноження. Знайдіть масу культури через: 30хв, 40хв, 1год, 3год, 4год, 6год. Побудуйте відповідний графік.

Показникова функція в медицині

Коли людина лякається, в кров виділяється адреналін, який потім руйнується, причому швидкість руйнування пропорційна кількості цієї речовини, що ще залишилася в крові.При діяльності хвороб нирок часто визначають здатність нирок виводити з крові радіоактивні ізотопи, причому їх кількість спадає за показниковим законом. Швидкість зміни кількості ліків у організмі пропорційна їх кількості.

Якщо А(t) - кількість ліків у тілі через час t, R₀ - швидкість надходження ліків до організму (стала – відома величина), k – коефіцієнт пропорційності (стала, що характеризує швидкість виведення ліків з організму), то

При відновленні концентрації гемоглобіну в крові донора або пораненого за показниковим законом спадає різниця між нормальним вмістом гемоглобіну і наявною кількістю цієї речовини. Як і при радіоактивному розпаді, лікарі розглядають період, за який розпадається або відновлюється половина речовини. Для адреналіну – частки секунди, для ізотопів – хвилини, для гемоглобіну – дні.

Звичайно, показниковий закон виконується дуже приблизно в біологічних системах, бо ми маємо тут справу з дуже складними системами.

Відчуття, які сприймаються органами чуттів, можуть викликатися подразненнями, що відрізняються одне від одного в мільярди разів. Удари молота по сталевій плиті в 100 млрд. разів голосніші, ніж шелест листя, а яскравість вольтової дуги в трильйони разів більша, ніж яскравість слабенької зірочки на нічному небі. Якби відчуття були пропорційні подразненням, то ніякі фізіологічні процеси не дозволили б дати такого діапазону відчуттів. Досліди показали, що організм ніби „логарифмує” подразнення. Це означає, що величина відчуттів приблизно пропорційна логарифмам величини подразнень.

Логарифмічна функція

Історія виникнення

Хто ж і коли „придумав” логарифми? Їх винахід пов’язаний з двома постатями: швейцарцем Іобстою Бюргі (1552-1632), знаним годинникарем і майстром астрономічних інструментів, і шотландцем Джоном Непером (1550-1617), який теж не був математиком за професією, астрономія була його „хобі”.

А Бюргі працював разом з астрономом Іоганном Кеплером, котрий встановив закони руху планет навколо Сонця. Саме величезний обсяг необхідних в астрономії обчислень і спонукав Бюргі і Непера шукати шляхів для їх спрощення. 20 років присвятив Непер своїм логарифмічним таблицям, аби, за його словами, „позбутися нудних і тяжких обчислень, які відлякують зазвичай багатьох від вивчення математики”. Обидва автори прийшли до своїх таблиць незалежно один від одного. Вони склали таблиці так званих натуральних логарифмів Бюргі працював над таблицями 8 років і видав їх у 1620 році під назвою „Арифметична і геометрична таблиця прогресій”. Проте його таблиці не отримали широкого поширення, бо Непер видав свій „Опис дивовижної таблиці логарифмів” на 6 років раніше. Тому й назвали число е неперовим числом.

Понад три з половиною сторіччя з тих пір, як у1614 році були опубліковані Непером перші логарифмічні таблиці, вони вірою і правдою служили астрономам і геодезистам, інженерам і морякам, скорочуючи час на обчислення і, як сказав французький вчений Лаплас (1749-1827), продовжуючи життя обчислювачам.

Ще донедавна важко було уявити собі інженера без логарифмічної лінійки в кишені. Винайдена в 1624 році англійським математиком Гунтером (1581-1626), вона дозволяла швидко одержувати відповідь з достатньою для інженера точністю до трьох значущих цифр. І хоч тепер її витіснили калькулятори і комп’ютери, проте можна сміливо сказати, що без логарифмічної лінійки не було б і перших комп’ютерів.

          Логарифми і ... музика

Розкопуючи одне з поселень кам’яного віку на території України, археологи знайшли кілька кісток мамонта, призначення яких було їм незрозуміле. Лише уважний аналіз показав, що на цих кістках залишилися сліди ударів – це були залишки шумового оркестру, під звуки якого стародавні люди виконували магічні танці. Пізніше помітили, що більш приємні звуки можна отримати, зробивши барабан або просвердливши шматок дерева, щоб вийшла сопілка. А звучання тятиви лука? Воно навело на думку про створення струнних інструментів.

Піфагор був не тільки математиком, а й хорошим музикантом. Він встановив, що приємні сполучення звуків відповідають певним співвідношенням між довжинами струн, що коливаються, або відстанями між дірочками сопілки. Саме він створив першу математичну теорію музики, і хоча музиканти не дуже люблять перевіряти „алгеброю гармонію”, вони весь час мають справу з математикою, бо сучасна гама ґрунтується на логарифмах. Зображення клавіш.

Будемо називати найнижчу октаву нульовою; а кількість коливань ноти do цієї октави за 1 секунду приймаємо за 1. тоді нота do першої октави буде робити в 2 рази більше коливань. Позначимо всі ноти хроматичної гами номерами р, приймаючи за нульовий основний тон кожної гами. Тоді тон sol буде 7-й, lа – 9-й і т. д., 12-й тон буде знову do, тільки октавою вище. Тому кожен наступний тон в разі має більше коливань, ніж попередній.

Позначимо N_pm - кількість коливань тому з номером р із m-ї октави.

Прологарифмуємо обидві частини основної рівності:

Звідси видно, що номери клавіш рояля являють собою логарифми кількості коливань відповідних звуків. Номер октави – характеристика (тобто ціла частина) логарифма, а номер звука в даній октаві – його мантиса (тобто дробова частина).

Полярні координати

Щоб задати систему полярних координат, вибирають точку О (полюс) і з неї проводять промінь (полярну вісь). Положення точки М на площині визначення двома числами: відстанню r від O до M і кутом φ між променем OM і полярною віссю (в радіанах).

Визначення положення точки за її полярними координатами використовувати, по суті, стародавні астрономи – довгота і широта і є полярними координатами на сфері. І зараз цими координатами користуються в походах за азимутом.

Якщо літак буде летіти, дотримуючись весь час одного курсу, тобто перетинаючи всі меридіани під одним і тим самим кутом, то його шлях зобразився на карті спіраллю, яка має назву логарифмічної. Її рівняння

При різних перетвореннях (гомотетії, повороті) вона залишається незмінною. Властивості цієї кривої так вразили Якоба Бернуллі, що він назвав її spira mirabilis (чудова спіраль) і заповів зобразити її на його могилі з написом Eatemmutata resurgo (перетворювана, відроджуюся знову).

          Мостобудування

Там, де зараз у Києві знаходиться міст Метро, до війни прикрашав Дніпро перший капітальний міст, який називався Ланцюговим. Його збудував у 1853 році англійський інженер де Віньйоль. У 1920 року під керівництвом Є. О. Патона міст було відбудовано, але на початку Великої Вітчизняної війни він знову був зруйнований.

Чому цей міст називався Ланцюговим?  Річ у тім, що ланцюг, вагою якого можна знехтувати і який підтримує рівномірно розподілений вантаж, провисає по параболі. Якщо ж прогин нитки викликаний її власною вагою, то форма нитки здається рівнянням:

 а – стрілка прогину,

Т₀ - натяг нитки в найнижчій точці, γ – її лінійна густина.

Мотузка, підвішена за кінці, телеграфний провід між двома стовпами, гнучкі нерозтягувані нитки провисають по цій кривій, яка називається ланцюговою лінією. Якщо стрілка прогину не дуже велика, то її форма нагадує параболу. Тому Галілей вважав, що ланцюгова лінія збігається з параболою. Але Гюйгенс довів, що це не так. При обертанні ланцюгової лінії навколо осі абсцис утворюється поверхня, яка називається катеноїдом („катена” – італійською „ланцюжок”). Ця поверхня має найменшу площу в порівнянні з усіма поверхнями, що проходять через 2 даних кола. Форму катеноїда приймає мильна плівка, обмежена двома кільцями.

          Інші застосування

У техніці часто застосовуються ножі, що обертаються. Сила, з якою вони тиснуть на матеріал, що розрізається, залежить від кута різання, тобто кута між лезом ножа і напрямом швидкості обертання. Для того щоб тиск був сталим, потрібно, щоб сталим залишався кут різання, а це буде в тому випадку, коли леза ножів будуть окреслені по дузі логарифмічної спіралі. Величина кута різання залежить від матеріалу.

У гідротехніці по логарифмічній спіралі вигинають трубу, що підводить потік води до турбіни. Завдяки такій формі труби втрати енергії при зміні напрямку течії в трубі виявляються мінімальними і напір води використовується з максимальною продуктивністю.

Живі істоти зазвичай ростуть в усіх напрямках, зберігаючи свою форму. Але мушлі (раковини) морських тварин можуть рости лише в одному напрямі. Щоб не дуже витягнутися в довжину, їм доводиться скручуватися, причому зростання відбувається так, що зберігається подібність мушлі з її початковою формою. А таке зростання може відбуватися лише по логарифмічній спіралі або її просторовим аналогом. Тому мушлі всіх молюсків, равликів, а також роги архарів закручені по логарифмічній спіралі. Можна сказати, що ця спіраль є математичним символом співвідношення форми і зростання. Великий німецький поет Йоганн-Вольфганг Гете вважав її символом життя і духовного розвитку.

По дугах логарифмічної спіралі розміщено насіння в соняшника. Один з павуків, епейра, сплітаючи павутиння, закручує нитки навколо центра по логарифмічних спіралях.

По логарифмічних спіралях закручені багато галактик, зокрема Галактика, до якої належить наша Сонячна система.

Справді, безмежні застосування показникової і логарифмічної функції у різних галузях природи, науки, техніки, мистецтва.

Говорячи про застосування логарифмічних функцій, треба мати на увазі те, що потреба в них найчастіше виникає там, де використовують показникові функції. Наприклад, нехай залежність атмосферного тиску від висоти місцевості над рівнем моря описана за допомогою показникової функції, тоді висота над рівнем моря визначається через атмосферний тиск за допомогою логарифмічної функції.

Крім того, за  допомогою логарифмічної функції моделюються деякі реальні процеси і явища:

•       залежність швидкості ракети v від її маси m задається формулою , де v_г – швидкість газів, що вилітають, m₀ - стартова маса ракети;
•    залежність коефіцієнта D звукоізоляції стін від тиску p звуку, що пройшов через стіну, задається формулою 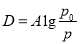, де p₀ – тиск звуку поглинання, А – деяка стала.

Логарифмічна функція застосовується у сейсмології. Наприклад, магнітуда об’ємних хвиль (показник землетрусу) обчислюється за формулою   , де А – амплітуда коливань землі (у мікрометрах), Т- період хвилі (у секундах), і Q – поправка, яка залежить від відстані до епіцентру D і глибини осередку землетрусу h.

ЗАДАЧА. Швидкість занурення тіла в рідину описується за допомогою формули , де v- швидкість, м/с; t- час, с.

1. Через скільки секунд після початку занурення швидкість дорівнюватиме 2,2м/с?
2. Через скільки секунд швидкість тіла становитиме 95% від максимальної?

ЗАДАЧА. Конструкція вакуум-насоса розрахована на відкачку за один хід поршня з камери 3% газу від тієї кількості , що була в камері перед цим ходом поршня. Скільки таких рухів треба зробити, щоб відкачати з камери 99% газу?

ЗАДАЧА. Кількість осіб біологічної популяції протягом кожної одиниці часу збільшується на 8% по відношенню до попередньої одиниці часу. Через скільки одиниць часу чисельність популяції подвоїться?

ЗАДАЧА. Тиск повітря спадає із зростанням висоти (при сталій температурі) за законом , де р₀-тиск на рівні моря (h=0), р- тиск на висоті h , Н- деяка константа, яка залежить від висоти. Знайдіть формулу для обчислення висоти залежно від тиску.

ЗАДАЧА. Культурі зі 100 бактерій надана можливість розмножуватися у сприятливих умовах за законом , де N – кількість бактерій у момент t ,N₀  - кількість бактерій у початковий момент часу (t=0),k - деяка константа. Через 12год виявляється, що культура містить 500 бактерій. Скільки бактерій буде через 2 доби після початку досліду?

ЗАДАЧА. Закон радіоактивного розпаду речовини має виглядде m₀ – маса речовини у початковий момент t=0, m - маса речовини у момент t , Т- деяка константа, яку називають періодом напіврозпаду. Через час Т після початкового моменту маса радіоактивної речовини зменшується вдвічі. Обчисліть період напіврозпаду речовини, якщо за рік її маса зменшилася у десятеро.

ЗАДАЧА. Швидкість v ракети в залежності від маси m змінюється за законом  (формула Ціолковського), де v_г – швидкість газів, що вилітають з ракети, m₀  - стартова маса ракети. Знайти залежність маси ракети від її швидкості.

ЗАДАЧА. Коефіцієнт звукоізоляції стін обчислюється за формулою , де p₀ – тиск звуку до поглинання, р- тиск звуку, що пройшов через стіну, А – деяка стала. Виразіть через інші змінні тиск звуку після поглинання.

ЗАДАЧА. Відсоткова ставка дорівнює 16%, нарахування відсотків проводиться кожні півроку. Скільки треба часу, щоб початкова сума подвоїлася?

Розв’язання.

, де п- кількість конверсійних періодів (загальна кількість нарахувань), r=0,16, m=2.

За умовою S=2P.

Отже, отримали рівняння 2P=P(1+i)n, можна поділити обидві частини рівняння на Р, про логарифмуємо, тоді   ln2=nln(1+i),

i=r: m=0,16:2, тому

Отже, початковий капітал подвоїться приблизно через 9 конверсійних періодів, а саме – через t=9:2=4,5року.

Подібні задачі можна розв’язувати у загальному вигляді для складних відсотків ,

де N- додатне число, яке показує кратність збільшення початкової суми; t – час (у роках), r – річна ставка (у відсотках), m – кількість нарахувань за рік; i=r:m – відсоткова ставка за конверсійний період.

ЗАДАЧА. Знайдіть відстань до зірки Вега α Ліри, якщо її видима та абсолютна величини 0,1 і 0,5.  М=0,1; М=0,5;М=m+5-5lgr; де  r – відстань від зорі, виміряна у парсеках.

Отже, r=8,1парсека(пк), 1пк=3,26св.р.=3^.10¹⁶м, тоді r=2,43^.10¹⁷м.

Відповідь: відстань до зірки Вега 2,43^.10¹⁷м.

ЗАДАЧА. Ємність легень людини виражається функцією

, де х – вік людини в роках (х>10); t(x) – ємність легень у літрах.

За допомогою графіка функції t(x) , зображеного на малюнку,установіть:

А) у якому віці ємність легенів людини максимальна і чому вона дорівнює;

Б) протягом якого часу ємність легенів більша ніж у 15 років.

Відповідь. а) у 20років ємність легень 5,7л;б) з 15 по30 років.

Похідна та її застосування

Раніше розглядалися елементарні методи дослідження функцій – математичних моделей багатьох реальних процесів і явищ. Але існують і нові методи – методи диференціального числення. Ці методи дають змогу зводити вивчення складного процесу до простішого – рівномірного, знаходити його швидкість і прискорення, визначати умови оптимального перебігу процесу, оцінювати допущені похибки, будувати і читати  графіки тощо. Використання похідної дозволить точніше зображати графіки функцій.

Поняття  похідної вводиться як границя відношення приросту функції до приросту аргументу.

ЗАДАЧА. Відомо, що для фірми витрати на випуск х одиниць продукції описуються функцією К(х)=0,002х³-0,3х²+20х+100(грн), а дохід одержаний від реалізації х одиниць продукції, можна обчислити за формулою R(x)=200x-0,05x(грн).Визначте приріст витрат і доходу для збільшення випуску одиниць продукції: а)з 20 до 100;б)з 30 до 50.

ЗАДАЧА. За деякими підрахунками визначено, що фірма, виробляючи х одиниць продукції щомісяця, має витрати К(х), що виражаються формулою К(х)=150+30х(грн), а дохід R(x), одержаний від продажу х одиниць цієї самої продукції, становить  R(x)= 90х-0,02х² (грн). Якщо фірма збільший щомісячний випуск продукції з 300 до 320 одиниць, як змініться її: а)витрати; б)дохід; в) прибуток?

Задачі , що приводять до поняття похідної

Розв’язання багатьох задач фізики, геометрії, техніки зводяться до однакових математичних побудов, які стали основою поняття похідної. Однією з таких задач є задача про знаходження миттєвої швидкості руху.

Якщо матеріальна точка рухається рівномірно, тобто за одинакові проміжки часу проходить той самий шлях, то швидкість її руху легко знайти: необхідно шлях, який пройшла точка за будь-який проміжок часу, поділити на час руху. Як відомо, при рівномірному русі залежність  шляху s від часу t виражається формулою s=vt , де v - швидкість руху, тобто є лінійною функцією.

Для характеристики нерівномірного руху застосовують поняття середньої швидкості руху на проміжок часу.

Середня швидкість руху точки на деякому проміжку часу – це відношення шляху, пройденого точкою за цей проміжок часу, до довжини цього проміжку. Середня швидкість нерівномірного руху, на відміну від швидкості рівномірного руху, залежить від проміжку часу, за який вона обчислюється.

Аналогічно можна міркувати про швидкість перебігу хімічної реакції, швидкість випаровування рідини і т. ін.

Поняття миттєвої швидкості зміни величини широко застосовується у природознавстві і техніці.

Сила струму є миттєвою швидкістю зміни кількості електрики, що проходить через поперечний переріз провідника.

Бачимо, що перебіг процесів описуються функціями.

ЗАДАЧА. Точка  рухається вздовж координатної осі. Закон ї руху має вигляд x=3t+2, де  x - координата точки,   t – час. З якою швидкістю  v рухається точка?

А. v =3;      Б. v=2;         В.  v=1,5.

ЗАДАЧА. При вільному падінні залежність між пройденою тілом відстанню s і часом t задається формулою , де g≈ 9,8м/с²- прискорення вільного падіння. Яку відстань пролетить тіло за другу секунду падіння?

А. 2gм;     Б. 1,5gм;       В. 0,5gм.

ЗАДАЧА. Маса солі, що розчинилася у воді за проміжок часу [0;t], дорівнює m(t). Що треба розуміти під :

А) середньою швидкістю розчинення солі за проміжок часу [1;2];

Б )швидкістю розчинення у момент часу t=1?

ЗАДАЧА. Точка здійснює гармонічні коливання за законом x=sin t, де x- координата точки, t≥0 – час руху. Знайти :

1. середню швидкість руху точки за проміжок часу ;
2. швидкість руху в момент часу  .

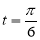З курсу фізики відомо , що важливою характеристикою руху матеріальної точки є прискорення. Математичний зміст цього поняття можна з’ясувати за допомогою похідної. У фізиці швидкість зміни швидкості називається прискоренням.

ЗАДАЧА. Матеріальна точка рухається за законом x=t²-3t+2 , де х- координата, м; t  - час, с. Знайти швидкість і прискорення точки в момент часу =4с.

ЗАДАЧА. Кутову швидкість рівномірного обертання визначають як відношення кута повороту до відповідного проміжку часу. Що розуміють під кутовою швидкістю нерівномірного обертання?

ЗАДАЧА. При нагріванні тіла зміна його температури описується законом T=0,4t+1 , де Т – температура , К; t  - час,с. З якою швидкістю нагрівається тіло?

ЗАДАЧА. Автомобіль протягом першої години пройшов 50км, а протягом другої  - 60км. Якою є середня швидкість автомобіля?

ЗАДАЧА.  Автомобіль   першу половину шляху долав із швидкістю 50км/год , а   другу половину  - із швидкістю  60км/год. Якою є середня швидкість автомобіля?

ЗАДАЧА.  Протягом деякого проміжку часу тіло рухалося за законом x=5t+1,а потім протягом такого самого часу – за законом x=7t-3. Якою є середня швидкість тіла?

ЗАДАЧА.  Відомо, що при вільному падінні тіла залежність пройденого шляху від часу виражається формулою , де s - шлях, м;  t - час,с; g≈ 9,8м/с²- прискорення вільного падіння.

1. Якою є середня швидкість тіла протягом  першої секунди падіння? Протягом першої хвилини падіння?

          2.Якою є швидкість тіла у момент t =1с; в момент t =10с?

ЗАДАЧА. Що слід розуміти під:

1. середньою швидкістю охолодження тіла за даний проміжок часу;
2. швидкістю охолодження тіла у даний момент часу?

 

 

Диференціювання функцій

Щоб знаходити миттєву швидкість точки за законом її руху або рівняння дотичної до графіка функції, треба навчитися знаходити похідні функцій.

ЗАДАЧА. Кинутий вертикально вгору камінь рухається за законом h(t)=4+8t-5t² , де h - висота над поверхнею землі, на яку піднявся камінь,м ; t  - час,с. Знайти:

1. швидкість руху каменя в момент його приземлення;
2. найбільшу висоту, на яку підніметься камінь.

ЗАДАЧА. М’яч  кинуто вертикально вгору. Якщо вісь х напрямлено до гори, то закон руху м’яча має вигляд: x=300t-5t² , де   x- координата,м;   t- час,с. Опускається чи піднімається м’яч у момент часу  t=32с?

ЗАДАЧА. Матеріальна точка виконує гармонічні коливання за законом x=2sinπt, де  x- координата точки, м;  t –час,с.

1. Знайти швидкість руху в моменти часу : ; ; .
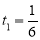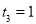
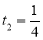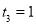2. У які моменти часу змінюється напрям руху точки?
3. У які моменти часу точка має найбільшу швидкість?
4.   ^*Доведіть, що прискорення руху пропорційне координаті точки. Чому дорівнює коефіцієнт пропорційності?

ЗАДАЧА. Точка рухається прямолінійно за законом x=2t³-3t²-12t+1, де  x – координата точки,м;  t –час,с ( t≥0).

1. Знайдіть прискорення у момент часу 3с.
2.   У який момент часу прискорення дорівнює нулю? З якою швидкістю рухається точка в цю мить?

Найбільше і найменше значення функції

Розв’язування багатьох практичних задач зводяться до визначення умов, за яких досліджувана величина набуває  свого найбільшого чи найменшого значення.

ЗАДАЧА ДІДОНИ. Фінікійська царівна Дідона, рятуючись від переслідувань свого брата, відправилась на захід вздовж берегів Середземного моря, де шукала собі притулку. На узбережжі Тунійської затоки вона почала вести переговори з Ярбом про купівлю для себе землі. І попросила вона землі для себе  зовсім  мало – стільки, скільки  можна «обгородити  шкірою бика». І коли Дідона і Ярб дійшли згоди, Дідона порізала шкіру бика на тоненькі смужки, зв′язала їх і обгородила ними немаленьку територію, чого Ярб не чекав. На ній Дідона побудувала фортецю, а  поблизу неї – місто Карфаген. То ж поміркуймо, яку найбільшу  кількість землі можна обгородити шкірою з бика? Мовою математики, яка із замкнених кривих, що має задану довжину може охопити найбільшу площу. Фактично, треба знайти найбільше значення деякої неперервної функції на відрізку. І кривою, що охоплює найбільшу площу є круг – найдосконаліша, на думку Піфагора, плоска фігура.

Наприклад: які розміри повинен мати ящик, щоб при певній кількості матеріалу, витраченого на його виготовлення, об’єм ящика був найбільшим? Як з круглої деревини виготовити прямокутну балку з найменшими витратами матеріалу? На якій висоті над центром круглого майдану потрібно підвісити ліхтар, щоб освітлення було найкращим? Як виконати певну роботу з найменшими витратами часу?

Подібні задачі розв’язуються за допомогою похідної.

ЗАДАЧА. Матеріальна точка рухається прямолінійно за законом x=t³-12t+10 . Знайти найбільшу і найменшу координату точки за проміжок часу [0;4].

При розв’язанні прикладних задач спочатку перекладають задачу  на мову математики, тобто будують її математичну модель.

ЗАДАЧА. У відділі пакування посилок приймають ящики, якщо сума їх довжин і обхвату не перевищує 150см. Знайти розміри ящика з квадратними боками, який задовольняє цю вимогу і має найбільший об’єм.

ЗАДАЧА. З трьох однакових дощок завширшки а см потрібно зробити жолоб, поперечний переріз якого мав би форму рівнобічної трапеції. Як це зробити, аби пропускна здатність жолоба була найбільшою?

ЗАДАЧА. Із наявного матеріалу можна зробити паркан завдовжки 320м. Визначте:

           1. як цим парканом обгородити прямокутну ділянку найбільшої площі, використавши з одного боку стінку будівлі;

 

 

           2. як цим парканом обгородити стадіон, що є прямокутним полем з півкруговою областю, приєднаною до однієї з його сторін, аби площа стадіону була найбільшою?

 

 

 

 

 

ЗАДАЧА.Площа прямокутного загону для страусів дорівнює 40000м². Якими мають бути його  розміри, щоб на огорожу пішло найменше сітки рабиця?

ЗАДАЧА. Треба загородити два пасовища у формі рівних прямокутників зі спільною стороною так, щоб сума їх площ дорівнювала 6га. Знайдіть найменшу можливу довжину огорожі.

ЗАДАЧА. Які мають бути розміри закритої коробки з квадратною основою, якщо її об’єм має дорівнювати V  і на її виготовлення необхідно витратити найменшу кількість матеріалу?

ЗАДАЧА. Якими слід робити літрові консервні банки циліндричної форми,щоб на їх виготовлення витрачалося найменше жерсті? Допусками на шви можна знехтувати. Об’єм циліндра дорівнює добутку площі його основи на висоту.

ЗАДАЧА. Визначити розміри такого відкритого басейну з квадратним дном і об’ємом V=32м²,щоб на облицювання його стін і дна було витрачено найменшу кількість матеріалу. У магазині є плитка розміром 20х30 за ціною 48грн за 1м² та плитка розміром 30х30 за ціною 52грн за 1м². Визначте, яку плитку вигідніше використати.

Розв’язування багатьох фізичних, біологічних, технічних і інших практичних задач зводиться до розв’язування  диференціального рівняння у^/=ky,(1) , де  k- задане число. Розв’язками цього рівняння є функції y=Ce^kx (2), де С-постійна, яка визначається умовами конкретної задачі.

Наприклад , у дослідах встановлено, що швидкість m^/(t) розмноження бактерій (для яких достатньо їжі) пов’язана з масою m(t) бактерій у момент часу t рівнянням m^/(t)= k m(t),де k – додатне число, що залежить від виду бактерій і зовнішніх умов. Розв’язками цього рівняння є m(t)= Ce^kx.

Постійну С можна знайти, наприклад, з умови, що в момент t=0 маса m₀ бактерій відома. Тоді m(0)= m₀₌ Ce^k.0=С, і тому  m(t)= m₀e^{k. t} .

Іншим прикладом застосування рівняння (1) є задача про радіоактивний розпад речовини. Якщо m^/(t)=-km(t),   де k –постійна, що залежить від радіоактивності речовини. Розв’язками цього рівняння є функції   m(t)=Ce^-kt  .

Якщо в момент часу t маса речовини дорівнює m₀ , то C=m₀ , і тому m(t)=m₀e^-kt (3).

Відзначимо , що на практиці швидкість розпаду радіоактивної речовини характеризується періодом напіврозпаду, тобто проміжком часу, протягом якого розпадається половина вихідної речовини.

Нехай Т – період напіврозпаду, тоді з рівності (3) при t=Т одержуємо

. Звідси   , .

У цьому випадку формула (3) при t=Т  запишеться так

, тобто   .

Застосування похідної

ЗАДАЧА. Зрошувальний канал має форму рівнобічної трапеції, бічні сторони якої дорівнюють меншій основі. Для якого кута нахилу бічних сторін трапеції переріз каналу буде мати найбільшу площу?

ЗАДАЧА. Прямокутну ділянку землі, яка прилягає до стіни будинку, потрібно обгородити парканом завдовжки 160м. знайти довжину цієї ділянки, за якої площа її буде найбільшою.

ЗАДАЧА. Витрати на паливо, що необхідне для руху океанського лайнера, пропорційні до куба його швидкості та становлять 20у.о. за 1год при швидкості 10 вузлів (1 вузол=1852м/год). Знайти най економнішу швидкість лайнера за тихої погоди.

 Отже, за допомогою похідної розв’язують багато задач із різних галузей  науки і практики.

Можна навести приклади часто вживаних формул, які містять похідну:

            ω(t)=φ^/(t)- кутова швидкість – похідна від кута повороту;

       a(t)= ω^/(t) – кутове прискорення- похідна від кутової швидкості;

       I(t)=q^/(t)-сила струму-похідна від кількості електрики;

       N(t)=A^/(t) - потужність –похідна від роботи;

       C(t)=Q^/(t)-теплоємність-похідна від кількості теплоти;

       P(t)=V^/(t)- продуктивність праці-похідна від обсягу продукції.

ЗАДАЧА.Сигнальна ракета летить вертикально вгору так, що її рух описується законом s(t)=98t-4,9t²(t-у секундах, s-у метрах). Знайдіть: а)швидкість ракети через 5с руху; б)на яку максимальну висоту долетить ракета.

ЗАДАЧА.Кількість теплоти Q(t), яка потрібна для нагрівання води масою 1кг від 0⁰С(0⁰< t <95⁰), наближено можна визначити за формулою

  Q(t)=0,396t+2,081^.10^-3.t²-5,024^.10^-7.t³ .

Установіть залежність теплоємності води C(t) від температури.

ЗАДАЧА. Тіло масою 10кг рухається прямолінійно за законом x(t)=t²+t+1 (t - у секундах, x - у метрах). Знайдіть:а)кінетичну енергію тіла через 5с після початку руху; б)силу, що діє на тіло в цей час.

ЗАДАЧА. Як залежить продуктивність праці молодого робітника від тривалості роботи, якщо обсяг виготовленої ним продукції виражається формулою V(t)=10+6t²-t³.

ЗАДАЧА. Робота, яку виконує двигун автомобіля, визначається формулою A(t)=15t²+360 (А(t)-в Джоулях,t - у секундах). Яку потужність розвиває двигун?

ЗАДАЧА. Маховик ,затримуваний гальмом, обертається за законом φ(t)=4t-0,3t² (час t – у секундах, кут φ(t) –   у радіанах). У який момент часу він зупиниться?

ЗАДАЧА. Обсяг продукції V цеху, який виготовляє дзеркала бокового огляду, протягом дня виражається залежністю V(t)= , де tϵ[1:8]. Обчисліть продуктивність праці  цеху протягом кожної години роботи.

Інтеграл та його застосування

Застосування визначених інтегралів

За допомогою визначених інтегралів обчислюють площі криволінійних фігур на площині, статистичні моменти, моменти інерції, роботу сили, потенціали. Наприклад, обчислюючи роботу сили, доводиться мати справу з функціями, аргументом яких є довжина кривої, відлічувана від певної точки на кривій, - криволінійна координата. До таких функцій застосовують такий самий обчислювальний процес, що й для знаходження визначеного інтеграла як границі інтегральних сум. Але шлях інтегрування не є прямолінійним відрізком осі абсцис, а є дугою певної кривої. Такий інтеграл називають криволінійним. Інтегрування застосовують до функцій кількох змінних і інтерпретують як обчислення об’єму, тобто запроваджують подвійні, потрійні і п-кратні інтеграли. Узагальнення криволінійних інтегралів приводить до поверхневих інтегралів. Досліджують також умови, які повинна задовольняти функція, щоб до неї можна було застосувати інтегрування.

Виникнення інтегрального числення пов’язане з потребою обчислення площ і об’ємів. Уже в античній математиці для обчислення площ і об’ємів застосовували способи, схожі на обчислення визначених інтегралів. Значних успіхів у цьому досяг давньогрецький математик Архімед (ІІІ ст. до н.е.), який для розв’язування задач на обчислення площ і об’ємів застосовував метод вичерпування.

Створенню інтегрального числення сприяли праці Й.Кеплера, Б.Кавальєрі, Е.Торічеллі, Дж.Валліса, Б. Паскаля. Математики ХУІІ ст. не користувалися поняттям границі. Замість цього вони говорили про «суму нескінченно великої кількості нескінченно малих доданків». Площу криволінійної трапеції вони уявляли складеною із вертикальних відрізків довжиною f(x), яким, проте, приписували площу, що дорівнює нескінченно малій величині f(x)dx. Шукана площа подавалася у вигляді суми нескінченно великої кількості малих площ . Іноді навіть підкреслювалося, що окремі доданки цієї суми нулі, але нулі особливі, в результаті додавання нескінченної кількості яких дістаємо цілком певну додатну суму. Учитель І.Ньютона І.Барроу встановив зв'язок між диференціюванням та інтегруванням у геометричній формі, а І.Ньютон і Г.Лейбніц незалежно один від одного в кінці ХУІІ ст. розробили для цих двох операцій системи позначень і правил, вказали на зв'язок між ними. З того часу це окремий розділ математики. Метод Ньютона-Лейбніца починається заміною кривої, що обмежує площу, яку треба знайти, послідовністю ламаних, що наближається до неї, аналогічно до методу вичерпування. Операція, обернена до диференціювання, називається інтегруванням.

У ХУІІІ ст. розвиткові інтегрального числення найбільше сприяли праці Якоба та Йогана Бернуллі, Ж.Лагранжа і особливо Л.Ейлера, який довів апарат інтегрального числення майже до сучасного стану.

У ХІУ ст. інтегральне числення перебудовують на рівні зрослих вимог математичної строгості О.Коші, Г.Ріман, К.М.Жордан. Важливі результати належать українському математикові М.В.Остроградському (перетворення п-кратного інтеграла на (п-1) -кратний та ін.) і російському вченому П.Л.Чебишеву (умови інтегрування диференціальних біномів та ін.).

У ХХ ст. розвитку інтегрального числення особливо сприяли праці французьких математиків (А.Лебег, Е.Борель, А.Данжуа) і радянських математиків (О.Я.Хінчин, М.М.Лузін, А.М.Колмогоров).

Походження  і розвиток інтегралу тісно пов’язані з розв’язанням багатьох практичних задач, наприклад, з обчисленням площ плоских фігур, знаходження шляху, пройденого тілом, визначення роботи з перенесенням вантажу тощо.

Якщо за допомогою похідної від координати за часом можна визначити швидкість руху точки, то операція інтегрування дасть змогу знайти координату точки за її швидкістю. Так само , якщо сила струму є похідною від заряду за часом, потужність – похідною роботи за часом, то за допомогою інтегрування можна обчислити заряд за даною силою струму, роботу – за відомою потужністю і т.ін.

Первісна

Поняття первісної для функції має широке застосування. Воно використовується там, де за швидкістю зміни величини треба відновити закон  зміни самої величини. Наприклад, за швидкістю прямолінійного руху точки потрібно встановити закон руху, за швидкістю зміни концентрації речовини – закон зміни концентрації, за швидкістю зміни біомаси популяції – закон зміни біомаси. Розв’язання цих задач зводиться до пошуку первісної, яка задовольняє початкові умови.

Розглянемо детальніше застосування первісних у механіці.

Нехай матеріальна точка масою т рухається прямолінійно за законом x=x(t) під дією сили F(t),напрям дії якої збігається з напрямом руху. Такий рух описується другим законом Ньютона: ma=F, де а – прискорення руху: . За допомогою похідної цей закон можна записати у такому вигляді: або . Звідси можна відновити закон її руху.

Як приклади можна розглядати також:

•       закон інерції (тіло, на яке не діє сила перебуває у стані  спокою чи рівномірного прямолінійного руху).
• Вертикальний рух під дією сили тяжіння.

ЗАДАЧА. Матеріальна точка рухається нерівномірно, її швидкість змінюється за лінійним законом. Яким є закон руху точки?

ЗАДАЧА. Матеріальна точка здійснює гармонічне коливання вздовж прямої зі швидкістю v=3sin(2t-1) , де v – швидкість, м/с; t - час,с. Чому дорівнює амплітуда коливання точки?

Інтеграл

Розв’язання багатьох прикладних задач зводиться до знаходження приросту первісної для заданої функції на деякому  проміжку.

При розгляді задачі про знаходження переміщення матеріальної точки, що рухається прямолінійно з певною швидкістю за визначений проміжок часу, робимо висновок, що переміщення точки дорівнює приросту первісної для функції на проміжку.

Задачу про знаходження шляху, пройденого точкою, що рухається прямолінійно, можна звести до задачі про знаходження площі деякої фігури, обмеженої графіком залежності швидкості від часу, віссю абсцис і двома вертикальними прямими, які відображають початковий і кінцевий час руху.

ЗАДАЧА. Матеріальна точка рухається прямолінійно зі швидкістю v=2sint , де v – швидкість, м/с;  t –час, с. Який шлях пройде точка за проміжок часу [0;π]?

ЗАДАЧА. Точка, рухаючись прямолінійно зі швидкістю v=t³, за деякий проміжок часу пройшла шлях S. Який шлях вона пройде за той самий проміжок часу, якщо її швидкість змінюватиметься за законом v=(2t)³?

ЗАДАЧА. Точка виконує гармонічні коливання зі швидкістю, залежність якої від часу виражається формулою v=sint, де v – швидкість, м/с;  t –час, с. Знайдіть шлях, пройдений точкою  за проміжок часу [0;π].

ЗАДАЧА. Швидкість точки змінюється за законом v=4t- t²,де v – швидкість, м/с;  t –час, с. Знайдіть шлях , пройдений точкою

• за перші 2с руху,
• за третю секунду руху,
• від початку руху до моменту, коли вона змінить напрям руху.

ЗАДАЧА. Знайдіть шлях , пройдений автобусом за час від початку гальмування (t=0) до повної його зупинки, якщо при гальмуванні швидкість цього автобуса змінювалася за  законом v=20-4t, де v – швидкість, м/с;  t –час, с.

ЗАДАЧА. Два об’єкти почали рух по прямій одночасно з однієї точки в одному напрямку. Їхні швидкості змінювалися за законами: v=2cost і ,де v – швидкість, м/с;  t –час, с.

• Який із об’єктів пройшов більший шлях за проміжок часу ?
•         Яка відстань була між об’єктами у той момент часу, коли перший із них уперше поміняв напрям руху?

Застосування інтеграла

ЗАДАЧА. Швидкість руху тіла задано рівнянням v(t)=5t-t²(м/с). Знайти шлях, який пройде тіло від початку руху до його зупинки.

 У момент зупинки швидкість тіла дорівнює нулю, тобто   5t-t²=0,  t(5-t)=0,   t₁=0,  t₂=5.

Отже, тіло зупинилося через 5с.

Шлях, який пройде тіло за цей час, обчислюється так:

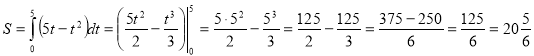(м).

Відповідь: (м).

ЗАДАЧА.  Для стискання пружини на 3см необхідно виконати роботу 16Дж. На яку довжину можна стиснути пружину, виконавши роботу 144Дж?

• За законом Гука, F=kx, тоді:

 

А₁=.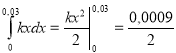

А=16Дж, тому , звідси   .

Отже, .

 Далі маємо:  .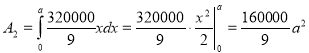

Але, А₂ =144Дж, тобто     ,   , а=0,09.

Тобто, пружину можна стиснути на 9см.

Відповідь: 9 см.

ЗАДАЧА. Обчислити силу тиску Р води на вертикальний шлюз з основою 18м і висотою 6м.

•   Сила Р рідини на вертикальну пластинку, занурену в рідину, обчислюється за формулою  .

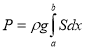Стінка шлюзу має прямокутну форму, тому S=18x, де 0≤х≤6. Густина води 1000кг/м³.

Тоді сила тиску води на шлюз буде:

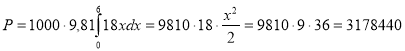(Па).

Відповідь: 3178440 Па.

ЗАДАЧА. Піраміда Хеопса – правильна чотирикутна піраміда висотою 147м, в основі якої є квадрат зі стороною 232м. Вона побудована з каменю, густина якого 2,5 г/см³. Знайти роботу проти сили тяжіння, втрачену при побудові піраміди.

ЗАДАЧА. Шків обертається з кутовою швидкістю ω= ,де t –час, с; ω - кутова швидкість, рад/с. На який  кут повернеться шків за третю секунду обертання?

ЗАДАЧА. Швидкість зміни концентрації речовини, що вступила в реакцію, виражається формулою v=3t+1 , де v - швидкість, моль/(с^.м³),t-час, с. Як зміниться концентрація речовини за час від t₁=0 до t₂=5с?

ЗАДАЧА (робота змінної сили). Матеріальна точка рухається вздовж осі х під дією сили y=F(x), спрямованої вздовж цієї прямої. Знайти роботу цієї сили з переміщенням точки з положення х=а у положення х=b.

ЗАДАЧА. Яку роботу потрібно виконати, щоб розтягти пружину на 3см, якщо сила в 10Н розтягує пружину на 1см?

ЗАДАЧА. Відомо, що сила струму І змінюється з часом  t за законом І=І(t). Виразіть за допомогою інтеграла заряд q, який проходить через поперечний переріз провідника за проміжок часу [t₀;T], якщо відомо, що І(t)=q^/(t).

ЗАДАЧА. Швидкість тіла, що рухається прямолінійно, змінюється за законом v=2+t-t², де v-швидкість, м/с; t-час, с. Знайти:

1. переміщення тіла за проміжок часу[1;3];
2. шлях, пройдений тілом за проміжок часу [1;3].

ЗАДАЧА. Колесо обертається з кутовою швидкістю, що змінюється за законом ω=2t+3, де ω-кутова швидкість, рад/с; t-час, с. На який кут повернеться колесо за проміжок часу [1;5]?

ЗАДАЧА. Швидкість нагрівання рідини змінюється за законом  v=0,2t+1, де v-швидкість нагрівання, К/с; t-час, с. На скільки кельвінів нагріється рідина за перші три секунди?

ЗАДАЧА. Швидкість зміни температури рідини v залежно від часу t виражається за формулою v=3t-2 (температура вимірюється в ⁰С, час – у секундах). На скільки градусів зміниться температура рідини за проміжок часу [1;4]?

ЗАДАЧА. Точка здійснює гармонічне коливання зі швидкістю v=3sin π/8t, де v-швидкість, м/с; t-час, с. Знайти:

1. переміщення точки за проміжок часу[0;16];
2. шлях, пройдений точкою за проміжок часу [0;16].

ЗАДАЧА. При стисканні пружини на 2см виконали роботу в 40 Дж. Яку роботу треба виконати, щоб розтягнути пружину на 3см?

ЗАДАЧА. Два одиничні електричні заряди розташовані на відстані 5см один від одного. Потім один із зарядів звільняється і віддаляється від іншого під дією сили відштовхування, яка, за законом Кулона, має вигляд ,  де r- відстань між зарядами, k –коефіцієнт пропорційності. Яку роботу здійснить сила, якщо заряд віддалиться на відстань: 10см; 15см?

ЗАДАЧА. Точка рухається прямолінійно зі швидкістю v=t²+1. Який шлях вона пройшла за проміжок часу [0;3]?

ЗАДАЧА. Швидкість м’яча, який кинули з поверхні землі вертикально вгору, змінюється за законом v=15-g t, де  v-швидкість, м/с; t – час с; g≈10м/с²-прискорення вільного падіння. На яку висоту підніметься м’яч за першу секунду?

ЗАДАЧА. Циліндричний бак, висота якого дорівнює 4,5м, а радіус основи дорівнює 1м, заповнений водою. За який час витече вода з бака через круглий отвір у дні бака, якщо радіус отвору становить 0,05м?

 

ЗАДАЧА. Обчисліть роботу сили F при стиску  пружини на 0,06м, якщо для її стиску на 0,01м потрібна сила 5Н.

ЗАДАЧА. Яку роботу потрібно витратити на стискання пружини на 4см, якщо відомо, що сила 2Н стискає цю пружину на 1см?

ЗАДАЧА. Сила 4Н розтягує пружину на 8 см. Яку роботу потрібно виконати, щоб розтягнути пружину на 8см?

ЗАДАЧА. Вода, що подається з площини основи в циліндричний бак через отвір у дні , заповнює весь бак. Визначіть затрачену при цьому роботу. Висота бака дорівнює h , радіус основи r .

ЗАДАЧА. Знайдіть роботу проти сил виштовхування під час занурення кулі у воду.

ЗАДАЧА. Для кращого обслуговування заїзду гонок серії «Формула-1» майстри визначили найкращий закон зміни швидкості  руху автомобіля прямою трасою: v(t)=2(t+2)^2,5 . Який шлях проїде пілот цієї гонки з 2-гої до 7-ої секунди від початку руху?

ЗАДАЧА. Знайдіть роботу, яку необхідно витратити на викачування води з резервуара, якщо він завглибше 4м і має форму циліндра радіусом 1м, ρ=10³кг/м³.

Диференціальні рівняння

Розв’язування багатьох  фізичних, біологічних, технічних і інших практичних задач зводиться до розв’язування диференціального рівняння y^/=ky, де k – задане число. Розв’язками цього рівняння є функції y=Ce^kx, де С – стала, яка визначається  умовами конкретної задачі.

ЗАДАЧА. Швидкість (t) розмноження бактерій пов’язана з масою m(t) бактерій в момент часу  t рівнянням m^/(t)=km(t), де k-додатне число, яке залежить від виду бактерій і зовнішніх умов. Розв’язком цього рівняння є функції m(t)=Ce^kt. Сталу С можна знайти із умови , що в момент t=0 маса бактерій m₀ відома. Тоді m(0)=m₀=C^k·0=C і тому m(t)=m₀e^kt.

ЗАДАЧА. Якщо m^/(t)- швидкість радіоактивного розпаду в момент часу t , то m^/(t)=- k m(t), де k-стала, яка залежить від радіоактивної речовини. Розв’язками цього рівняння є функції m(t)=Ce ^–kt. Якщо в момент часу t маса дорівнювала m₀, то С= m₀ і тому m(t)= m₀e ^–kt. Слід зазначити, що на практиці швидкість розпаду радіоактивної речовини характеризується періодом піврозпаду, тобто, проміжком часу, за який розпадається половина даної речовини. Нехай Т-період піврозпаду, тоді при t=T маємо ,звідси . Отже, .

У житті часто зустрічають процеси , які періодично повторюються, наприклад коливальний рух маятника, сируни, пружини і т.д.; процеси, пов’язані з електричним струмом, магнітним полем тощо. Розв’язування багатьох таких задач зводиться до розв’язування рівняння , де ω- задане додатне число, y=y(x), y^//=(y^/(x))^/. Функцію (y^/(x))^/  називають другою похідною функції у(х) і позначають  у^//(х)  або коротко  у^//. Розв’язком рівняння    у^// = - ω²y є функції    , де С₁, С₂ – сталі, що визначаються умовами конкретної задачі. Рівняння  у^// = - ω²y називають диференціальним рівняннням  гармонічних коливань, а  - розв'язком гармонічних коливань.

Елементи теорії ймовірностей і математичної статистики

Елементи комбінаторики

Представникам різних професій доводиться розв’язувати задачі, в яких з деякої множини об’єктів  потрібно вибирати елементи, що мають ті або інші властивості, розміщувати ці елементи в певному порядку. Так  керівнику цеху потрібно розподілити кілька видів робіт між працівниками, агроному – розмістити посіви сільськогосподарських культур на кількох полях, хіміку – розглянути можливі зв’язки між атомами і молекулами. Оскільки в таких задачахйде мова про комбінування об’єктів, їх називають комбінаторними задачами.

В наш час комбінаторні задачі приходиться розв’язувати фізикам, хімікам, біологам, економістам, спеціалістам самих різних професій.

ЗАДАЧА. Одна учениця має 7 книг із ручної вишивки, а друга -9 книг по машинній вишивці. Скількома способами можна обміняти одну книгу першої учениці на одну книгу другої учениці?

ЗАДАЧА. У крамниці продаються 5 різних видів виделок, 3 різні типи ножів і 4 різні види ложок. Скількома способами можна підібрати комплект із виделки, ножа і ложки?

ЗАДАЧА. У магазині є три види печива і десять видів цукерок. На десерт можна подати або печиво або цукерки. Скількома способами можна це зробити?

ЗАДАЧА. Скількома способами 6 різних тістечок можна розподілити між трьома учнями?

ЗАДАЧА. У групі кожен учень вивчає принаймні одну іноземну мову: англійську або німецьку. 25 учнів вивчають англійську, 10 учнів – німецьку , а 5 вивчають обидві мови. Скільки учнів у групі? Скільки з них вивчають лише німецьку мову?

ЗАДАЧА. Скількома способами можна розставити на п’ятимісному сушилі п’ять різних тарілок?

ЗАДАЧА. Скількома способами можна розставити на десятимісному сушилі п’ять різних тарілок?

ЗАДАЧА. Їдальня приготувала на сніданок 3 другі страви (А,В,С)і два напої (М,К). Скільки різних наборів можна вибрати на сніданок? Складіть відповідну діаграму-дерево.

ЗАДАЧА.Їдальня приготувала на обід 3 перші страви(А,В,С), 3 другі (а,в,с) і 3 треті (х,р,у). Скільки різних наборів із трьох страв можна вибрати на обід? Складіть відповідну діаграму-дерево.

ЗАДАЧА. Із ящика, який містить 20 придатних і 5 бракованих підшипників, навмання витягують три деталі. Чому дорівнює ймовірність того, що: 1) усі підшипники придатну, 2) придатні лише два підшипники?

ЗАДАЧА. Ящик містить як придатні так і браковані гільзи до автомобіля. Для перевірки відбирають без повернення 10деталей. Отримана вибірка впорядкована чи невпорядкована?

ЗАДАЧА. У майстерні , де виготовляють ключі, є 12 типів заготовок. Із кожної заготовки можна виготовити ключ, зробивши виступ в одному з п’яти місць. Розмір виступу на кожному місці може набувати трьох різних значень. Скільки різних типів ключів може виготовити майстерня?

ЗАДАЧА. У класі 25 учнів. Щодня призначається один черговий. Скількома способами можна скласти розклад на 5 днів так, щоб жоден учень не чергував більше одного разу?

ЗАДАЧА.  Скількома способами з 10 спортсменів можна відібрати 4 способи для участі:

1. у змаганнях з бігу на 100метрів,
2. в естафеті 100м+200м+400м+800м?

ЗАДАЧА. Із коробки , яка містить 3 білих ґудзики та 7 червоних ґудзиків, навмання витягують одразу два ґудзики. Знайдіть імовірність того, що : 1) обидва ґудзика червоні, 2) обидва ґудзика білі, 3) один ґудзик білий а один червоний.

ЗАДАЧА. Завод виготовляє паливні баки. Для контролю відібрано п=1000 баків, серед яких бракованих виявилося m=120. Оцініть ймовірність того, що виготовлений бак бракований.

Поняття теорії ймовірностей

Більшість явищ навколишнбого світу має випадковий характер, і людині часто доводиться висувати припущення, прогнозувати розвиток ситуації, розмірковувати про можливість підтвердження тієї чи іншої гіпотези.

Закономірності, які властиві кожному явищу, проявляють себе через сукупність випадковостей. Для багатьох явищ вплив випадку є настільки суттєвим, що дослідження їх неможливе без вивчення і кількісної оцінки такого впливу. Теорія ймовірностей розглядає математичні моделі явищ, що враховують вплив випадку. Аналізом результатів , одержаних за допомогою ймовірнісних моделей, займається математична статистика. Вона розробляє методи, які дають змогу за результатами випробувань робити певні висновки щодо процесів та явищ, що вивчаються.

ЗАДАЧА. В магазині є 11 покупців. Ймовірність здійснення покупки кожним із них дорівнює 0,1. Яка ймовірність того, що 7 із них здійснять покупку?

ЗАДАЧА. Із 30 кавунів 20 кавунів спілих. Вибирається два кавуна. Яка ймовірність того, що вибрані кавуни спілі?

ЗАДАЧА. Випущено  сто лотерейних білетів з одинадцятьма грошовими виграшами, з яких вісім – по 10грн., два-по 50грн. і один-100грн. З куплених 25 білетів три виграли по 10грн. і один виграв 50грн. Інші залишилися без виграшу. Порівняйте ймовірність р події «куплений білет безвиграшний »  при купівлі одного білета і частоту v  цієї події в описаному експерименті.

ЗАДАЧА. Імовірність того, що при натисканні стартера мотор запрацює, дорівнює . Знайдіть імовірність того, що для запуску мотора потрібно буде зробити не більше, як два натискання.

 Р(А₁)=Р(А_і)= , де подія А_і полягає в тому, що мотор запрацював при і-му натисканні стартера. Якщо подія А полягає в тому, що для запуску мотора потрібно буде не більше як два натискання, то

Р(А)=1-(1-)²=1-=.

ЗАДАЧА. В коробці є 20 деталей, із яких 15 стандартних. Знайти ймовірність того, що серед 3 вибраних навмання деталей є хоч би одна стандартна.

ЗАДАЧА. В майстерні працює 3 станка. За зміну перший станок може потребувати наладки з ймовірністю 0,1, третій – з ймовірністю 0,12. Вважаючи, що станки не можуть потребувати наладки одночасно, знайти ймовірність того, що за зміну хоча б один станок потребує наладки.

ЗАДАЧА. За статистичними даними ремонтній майстерні в середньому на 20 зупинок токарного станка приходяться: 10-для заміни різця; 3-через несправності привода; 2-через несвоєчасну подачу заготовок. Останні зупинки відбуваються за інших причин. Знайти ймовірність зупинки станка за інших причин.

ЗАДАЧА. Є три ящики, в яких містяться по 10 деталей. В першому ящику 8, в другому 7 і в третьому 9 стандартних деталей. Із кожного ящика навмання беруть по одній деталі. Знайти ймовірність того, що всі три деталі будуть стандартними.

ЗАДАЧА. Завод випускає 95% деталей стандартними, причому із них 86% - першого сорту. Знайти ймовірність того, що навмання взята деталь виготовлена на цьому заводі буде першого сорту.

ЗАДАЧА. В двох ящиках знаходяться деталі: в першому – 10 (із них 3 стандартних); в другому – 15 (із них 6 стандартних). З кожного ящика навмання беруть по одній деталі. Знайти ймовірність того, що :

1) деталь з першого ящика стандартна;

2) деталь  з другого ящика стандартна;

3) обидві деталі стандартні;

4) обидві деталі не стандартні;

5) хоч би одна деталь не стандартна;

6) хоч би одна деталь стандартна.

ЗАДАЧА. При виготовленні деталі проводиться чотири операції. Ймовірність одержання брака після кожної операції дорівнює 0,01. Яка ймовірність випуска деталі без брака, якщо операції незалежні.

ЗАДАЧА. Для інформування про аварію встановлено три незалежні між собою сигналізатори. Ймовірність того, що під час аварії спрацює перший сигналізатор р₁=0,95, другий – р₂=0,9, третій –р₃=0,86.

1. Знайдіть ймовірність того, що під час аварії спрацює тільки один сигналізатор.
2. Знайдіть ймовірність того, що під час аварії спрацюють тільки два сигналізатори.
3. Знайдіть ймовірність того, що під час аварії спрацюють усі три сигналізатори.
4. Знайдіть ймовірність того, що під час аварії не спрацює жодний сигналізатор.
5. Знайдіть ймовірність того, що під час аварії спрацює принаймі один сигналізатор.

          ЗАДАЧА. Ймовірність того, що витрата електроенергії протягом доби не перевищує встановленої норми, дорівнює 0,75. Знайдіть ймовірність того, що в найближчі 6 діб витрати електроенергії впродовж 4 діб не перевищують норми.

ЗАДАЧА. В цеху 6 двигунів. Для кожного двигуна ймовірність того, що він у даний момент включений, дорівнює 0,8. Знайти ймовірність того, що в даний момент : а) включено 4 двигуни; б)включені всі двигуни; в) виключені всі двигуни.

ЗАДАЧА. 75% продукції, що виготовляє завод, є продукцією вищого сорту. Яка ймовірність того, що із 6 навмання взятих виробів 3 вироби будуть вищого гатунку?

ЗАДАЧА. Два станка працюють незалежно один від одного. Ймовірність безперебійної роботи протягом години для першого станка становить 0,75, а для другого -0,8. Яка ймовірність того, що протягом години будуть збої тільки одного станка?

ЗАДАЧА. В партії із 10 деталей 8 стандартних. Знайти ймовірність того, що серед навмання вибраних 2 деталей вони будуть стандартними?

ЗАДАЧА. Вироби містять 5% браку. Знайдіть ймовірність того, що серед 5 виробів будуть два бракованих?

ЗАДАЧА. Твій товариш забув дві останні цифри PIN-коду своєї банківської картки.

1. Яке найбільше число спроб знадобиться йому для відновлення коду?
2. Яка ймовірність того, що він з першої спроби відновить код?
3. Порадь товаришу, що необхідно зробити, якщо після третьої невдалої спроби картку було заблоковано.

Випадкове випробування і випадкова подія

У реальному житті ми на кожному кроці зустрічаємося із явищами, результат перебігу яких не можна заздалегідь передбачити. До таких явищ належать: страхування людини від нещасного випадку або майна, транспортних засобів(неможливо однозначно передбачити; чи трапиться та пригода, від якої проводиться страхування); вантажні роботи в порту (неможливо точно вгадати, скільки часу займуть вантажні операції на тому чи іншому судні); гра у рулетку (заздалегідь неможливо знати, в якому секторі зупиниться кулька).

Є випробування, які можна провести багаторазово: купити багато лотерейних білетів, багато разів кидати гральний кубик, багато разів витягати кільку із скрині, стріляти по мішені, грати у рулетку, застрахувати багато людей, розвантажити багато суден. Розглядувані випробування проходять приблизно в однакових умовах. Наслідки цих випробовування неоднозначні.

ЗАДАЧА. Які із наступних випробовувань можна вважати випадковими:

• стрільба по мішені,
• нагрівання води у чайнику,
• купівля лотерейного білета,
• обертання рулетки у грі «Поле чудес»,
• вступ юнака до ліцею,
• багаторічні спостереження над погодою в той самий день року в одній і тій самій місцевості,
• підкидання кнопки,
• участь футбольної команди у першості області.

Відносна частота випадкової події

ЗАДАЧА. Деяке підприємство виробляє масову продукцію. Якщо виріб, що надійшов у продаж, виходить з ладу протягом одного року, то його замінюють запасним. Скільки запасних виробів необхідно виготовити, якщо протягом року продають N виробів? Для спрощення припустимо, що вихід з ладу запасного виробу неможливий.

ЗАДАЧА. Для контролю за якістю продукції швейної фабрики з кожної партії готових виробів відбирають на перевірку 150 виробів. Перевірку не витримують, у середньому, 6 виробів. Як оцінити ймовірність випуску бракованих виробів фабрикою: а) в даний час; б) після вдосконалення технології виробництва?

ЗАДАЧА. У скриньці лежать декілька однакових за розмірами котушок із нитками трьох кольорів: чорні, білі і коричневі. Зі скриньки взяли навмання 4 котушки ниток. Чи будуть серед узятих котушок напевно:

1. хоча б дві з чорними нитками,
2. хоча б дві з нитками одного кольору,
3. хоча б три з чорними нитками,
4. хоча б три з нитками одного кольору?

Наведіть приклади випадкових, зокрема , достовірних, неможливих подій, пов’язаних із розглянутим дослідом.

ЗАДАЧА. Відносна частота постільної білизни для дорослих, проданої у магазині за день, дорівнює 0,6. У цей день продали 24 комплекти дитячої постільної білизни. Скільки комплектів білизни продали у цей день?

ЗАДАЧА. Для перевірки якості було досліджено 200 халатів , серед яких 5 виявилися бракованими. Якою можна вважати ймовірність того, що навмання взятий халат буде: 1)придатним, 2)бракованим? Скільки бракованих халатів виявиться , в середньому, в партії із 1000 виробів?

Вибірковий метод у статистиці

Об’єктивний аналіз будь-яких масових явищ та процесів потребує наукових методів збору, обробки даних та інтерпретації отриманих результатів.

Статистика навчає збирати , зображати, сприймати, застосовувати інформацію, пов’язану з різними масовими явищами, процесами, подіями.. Головними методами для збору інформації  є опитування, проведення експериментів, використання паперових, електронних джерел інформації.

Предметом вивчення статистики є кількісна сторона явищ. Статистика вчить, як проаналізувати інформацію, виявити та оцінити закономірності формування, розвитку та взаємодії складних за своєю природою соціально-економічних явищ.

Математична статистика – розділ математики, присвячений математичним методам систематизації, обробки та дослідження статистичних даних для наукових і практичних висновків. Її широко застосовують соціально-економічні дисципліни та інші галузі, а саме: астрономія (розподіл і рух зірок у небесному просторі), фізика (термодинаміка), біологія (закони спадковості), гідрологія ( прогноз погоди), індустрія (контроль якості виробів).

Глибоке вивчення сучасної математичної статистики неможливо без допомоги теорії ймовірностей.

Статистика виникла з практичних потреб людини, її господарської діяльності, необхідністю обліку земельних угідь, майна, кількості населення, вивчення його занять, вікового складу.

Першим етапом будь-якого дослідження є збирання інформації, а саме, статистичне спостереження. Статистичне спостереження – це спланований, науково організований збір масових даних про соціально-економічні явища та процеси.

Прикладами статистичних спостережень можуть бути :  щоденний облік відвідування, облік успішності за семестр, перепис населення, анкетування, перелік релігійних громад країни, обстеження фінансової діяльності інвестиційної компанії, реєстрація шлюбів, опитування окремих учасників презентації, облік числа зареєстрованих злочинів, реєстрація рівня цін на продукти, телефонне опитування.

ЗАДАЧА. Що потрібно знати, окрім середнього числа відмов приладу, щоб оцінити загальну кількість відмов приладів? 

ЗАДАЧА. Потрібно з’ясувати потребу населення деякого міста в певному товарі. Як може допомогти поняття середнього арифметичного у вирішенні цієї проблеми?

ЗАДАЧА. Унаслідок ДТП в середньому 61% загиблих складають водії-непрофесіонали,  15%- мотоциклісти, 5% водії вантажних або службових машин, 4% - велосипедисти. Яка зі статистичних характеристик найкраще характеризує ситуації на дорогах?

ЗАДАЧА. Зібрано дані про тарифний розряд робітників цеху. Серед них 4 робітники мають перший розряд,6-другий, 12- третій,16-четвертий, 44- п’ятий, 18- шостий. Чому дорівнюють мода і медіана наведеної сукупності? Яким є їхній зміст?

ГЕОМЕТРІЯ

Математика характеризується тим,що не має певного матеріального об’єкта досліджень, конкретного класу явищ чи предметів реальної дійсності. Об’єктом математики є просторові форми і кількісні відношення дійсного світу, тобто абстраговані від реальності найзагальніші властивості та зв’язки предметів і явищ. Законам матеріального світу в математиці відповідають зв’язки абстрактно-логічного характеру між математичними поняттями.

Абстраговані від реальної дійсності, математичні поняття самі по собі не мають безпосередніх матеріальних прообразів, а тому може здатися, що математичні теорії не пов’язані з навколишнім світом.

Зв’язки математики з дійсністю виявляються насамперед у процесі застосування її понять і методів.

На уроках геометрії є великі можливості показати вирішальний вплив практичних потреб людського суспільства на розвиток геометрії.

Геометрія завжди мала численні практичні застосування. Основними її споживачами були землеміри, будівельники, художники. Землемірам потрібні були правила вимірювання ділянок землі, будівельники, користуючись геометрією, креслили план споруди, а потім зводили її, користуючись певними виробленими протягом століть правилами, згідно з якими певні геометричні форми частин споруд були пов’язані з умовами їх міцності.

Будівельники використовували також правило пропорційного поділу. Ремісникам потрібні були поняття про геометричні фігури та форми, про об’єми геометричних тіл. Використовували вони й правило пропорційного поділу. Завданя художників було складнішим: їм потрібно було відтворити на двовимірній площині те, що відбувається у тривимірному просторі. Для цього їм довелося розробити своєрідну геометрію-рід проективної геометрії.

Потреби розв’язувати задачі фортифікації та оборони фортець зумовили створення в останій чверті XVIII ст. ще однієї галузі геометрії – нарисної геометрії.

Ідеї геометрії – одна з основ, на якій у ХІХ ст. була створена сучасна теорія проектування будівельних споруд, а  також загальне машинобудування.

Розвиток і вдосконалення методів геометрії істотно зумовлюється потребами фізики, зокрема теорії відносності. Евклідова геометрія є тільки однією з можливих математичних моделей реального фізичного простору, яка відображає найпростіші його властивості і задовольняє практичні потреби людини, пов’язані з макротілами в земних умовах. А властивості простору, які виявляються в мікросвіті й великих космічних масштабах, моделює так звана неевклідова геометрія.

Важливим є пізнавальний аспект професійного орієнтування, який полягає у предметному ознайомленні учнів з формою, величиною і іншими властивостями матеріалів.

Зокрема, вибір форми виробу визначає і кількість відходів (тобто процент використання сировини), і витрати праці на обробку, і спосіб пакування, транспортування та зберігання. Ця форма визначає і конструктивні можливостя деталі, коли вона використовується для тих чи інших вироьів.

Геометричні міркування під час виконання багатьох робіт часто бувають вирішальними.

Геометрія допомагає визначати площі різних поверхонь, що важливо не лише для сільського господарства, а й для будівельних робіт, для розрахунків, повязаних з пошивом одягу, з обчисленням витрати палива, знаходити об’єми тіл, які потрібні при розрахунках витрати матеріалів під час будівельних робіт.

Розрахунки роботи багатьох машин і приладів грунтуються на відповідних властивостях геометричних фігур.

Різні вироби як важкої (верстати, двигуни, пристрої, інструменти тощо), так і легкої (взуття, головні убори, посуд тощо) промисловості випускають серіями. При визначенні розмірів в основу кладуть подібність фігур.

При будівництві шляхів заокруглення на поворотах здійснюють за допомогою спеціально дібраних кривих ( не лише кола).

Використання задач практичного змісту виконують профорієнтаційну функцію. Розв’язуючи їх, учні дістають важливу інформацію про роботу механізмів і верстатів, деяких приладів і пристроїв, про ряд трудових прийомів.

У шкільному курсі геометрії є можливості показати, що красиві форми речей і деталей спираються на математичні співвідношення, на теореми і формули, які спеціально вивчаються за програмою або використовуються в процесі розв’язування задач.

Наприклад, під час вивчення питання про дотичну до кола учні зустрічаються зі спряженням ліній. Плавний перехід від кривої (зокрема, від дуги кола) до прямої широко використовується у будівельній техніці.

Доцільно згадати про криві на шляхах. Коли намічають трасу майбутнього шляху (автомобільного або залізничного), то визначають прямолінійні відрізки. Але ні автомобіль, ні поїзд не рухатимуться по ламаній. Через це на кожному в кут вписується коло певного радіуса (його величина встановлюється з урахуванням особливості місцевості і передбачуваної швидкості руху). Таким чином, рух відбуватиметься то по прямій, то по дузі кола.

Ще складнішими є такі комбінації прямих і кривих при різних поворотах у гірській місцевості. Подані на плані, вони особливо красиві.

Спряження ліній використовується і в машинобудуванні. Спеціалісти намагаються уникати загострень деталей, бо такі загострення можуть викликати травми робітників. «Скруглювання » сприяє також економії металу. Разом з тим досягається і естетичний ефект: плавні лінії приємні для зору.

Особливо приємними для зору є геометричні форми, підпорядковані закономірностям так званого золотого поділу (перерізу) – поділу відрізка на дві частини, що відношення всього відрізка до більшої частини дорівнює відношенню частин. Величина цього відношення . Таку величину має відношення діагоналі правильного п’ятикутника до його сторони, зустрічається воно і в інших фігурах.

З поняттям про золотий переріз відрізка були обізнані ще піфагорійці, які вміли будувати правильний опуклий п’ятикутник. Уперше задачу про золотий переріз сформулював Евклід у «Началах»(ІІ книга).

У Стародавній Греції золотий поділ широко використовували як архітектори (Парфенон в Афінах), так і скільптори (статуя Аполлона).

Існує правило , за яким лоб, ніс і нижня частина обличчя красивої людини повинні мати однакові розміри. У людини, обличчя якої здається особливо пропорційним, рот ділить нижню частину обличчя, а дуги брів – усе обличчя у золотому відношенні.

Ще в давні часи помічено, що прямокутник, у якому сторони становлять частини відрізка, поділеного за правилом золотого поділу, справляє приємне зорове враження. Тому такої форми спеціально надають багатьом предметам: поштовим листівкам, маркам, картинам, книгам. Золотий переріз застосовується в таких, здавалося б, віддалених од математики питаннях, як теорія віршування, музика, архітектура, естетика, живопис.

Прекрасне в математиці включає й інші грані включає й інші грані. Так , ще до знаходження остаточного результату, який, можливо, буде названий прекрасним, глибоку внутрішню насолоду, задоволення людині приносить сам пошук результату, шлях до нього. Саме потягом до краси зумовленні численні пошуки нових доведень уже доаедених теорем, створення нових практичних задач.

Математична діяльність учнів має бути також безперервним пошуком, у процесі якого відкривають для себе математику.

Основні властивості фігур

Математика, у тому числі й геометрія, є однією з найдавніших наук. Історія людства налічує понад 2 мільйони років. Вже первісним людям доводилося лічити. Не могли люди не звернути увагу  також і на форми речей: щоб виготовити наконечники стріли або списа, видовбати човен із стовбура, треба було придивлятися до відповідних форм камінців, стовбурів дерев. Фіксуючи найрийнятніші форми, люди навчилися виготовляти посуд, пристосування для роботи і полювання, обладнувати житло.

З розвитком людського суспільства нагромаджувалися знання про форми і властивості цих форм, що сприяло удосконаленню трудових процесів, пов’язаних з будівництвом каналів, городищ і різних за призначенням споруд.

Перехід до осідлого землеробства висунув проблему вимірювання земельних ділянок. З’явилися й перші фахівці у цій галузі – землеміри. Щоб краще виконувати свої професійні  завдання , вони змушені були виявляти і вивчати властивості різних форм та фігур.

Грандіозні єгипетські піраміди, дивовижні споруди в Америці, Індії, Китаї, багатьом з яких по кілька тисяч років, свідчать, що вже в сиву давнину люди багато знали про форми речей і вміло застосовували ці знання.

Математика стала наукою лише в VІІ-VI століттях до н.е. – з того часу, коли в ній почали не лише описувати фігури та їх властивості, а й обгрунтовувати наявність цих властивостей, доводити правильність висловлених про ці фігури тверджень.

Про точку і пряму можна подати лише коротку довідку.

Термін «точка» походить від дієслова «ткнути», первісний зміст – наслідок миттєвого уколу (латинське pungo – «колю»). Термін «лінія» походить від латинського linea, що означає «лляна нитка». Спочатку під лінією розуміли тільки пряму (натягнену нитку, вірьовку ), але вже в IVст. До н.е.поняття лінії розширилося, і пряму вважали лише одним із видів ліній.

За основну одиницю довжини – метр узято 1/40000000 довжини земного меридіана. Еталон метра зберігається у містечку Севр, що поблизу Парижа, в спеціальній камері ( у якій температура і вологість повітря підтримуються майже сталими). Поняття довжини відрізка у евклідові геометрії не означується. Варто при цьому розглядати задачі на рух.

Градусне вимірювання кутів появилося у вавілонян приблизно 45 віків тому. Перехід до осідлого землеробства обумовив потребу ведення календаря, а він міг базуватися лише на даних астрономії. Тому не випадково у Вавілоні велися систематичні спостереження за сузір’ями і планетами, за їх видимими переміщеннями по небесній сфері. При цьому помітили, що діаметри видимих кругів у Сонця і Місяця майже однакові, причому в половині кола, яке описують над горизонтом, вкладаються 180раз. Це і привело до думки поділити розгорнутий кут на 180 рівних частин.

До XVII століття у грецьких і європейських математиків йшлося лише про кути , не більші від розгорнутого. Вчення про кути довільної величини з’явилося значно пізніше.

Термін «градус» - походить від латинського gradus, буквально означає «крок». Сучасні позначеня градусів та їх частин (мінут, секунд) увів в 1558р. французький лікар і математик Пелетьє.

Моряки поділяють розгорнутий кут на 16 рівних частин – румбів.

У військовій справі розгорнутий кут поділяють на 30 частин, які називають великими поділками кутоміра.

Вимірюють кути на площині за допомогою  транспортира. При вимірюванні кутів на місцевості використовують спеціальні кутомірні інструменти – теодоліт, гоніометр, астролябію.

Кути

Моделі суміжних кутів відомі людям давно. Уявлення про такі кути складється під час розгляду шляхів чи каналів, які перетинаються, при спорудженні внутрішніх стін будинків.

Ознаки рівності трикутників

Питанню рівності фігур приділяється велика увага. Масове промислове виробництво повязане із стандартизацією. Зокрема, встановлюються розміри окремих деталей і зазначаються допустимі відхилення від них. Саме тому, наприклад, гайки, виготовлені в певному цеху, можна використовувати не лише для якогось конкретного автомобіля, а й для будь-яких автомобілів , де є болти такого самого діаметра. Щоб стандартів було додержано, на кожному підприємстві є служба контролю, працівники якої стежать за тим, щоб кожна деталь і весь виріб в цілому мали встановлені розміри. Контроль здійснюється не на око і не прикладанням однієї фігури до іншої (або до еталону) – існує контролююча апаратура , розроблено прийоми і методи котролю.

Трикутник є однією з найпоширеніших геомнетричних фігур , у багатьох технічних виробах використовуються трикутні деталі або їх частини. Порівнювання двох трикутників часто є елементом порівнювання двох складніших геометричних фігур.

Порівнювати за розмірами дві геометричні фігури накладанням не тільки не просто, а в реальних умовах іноді взагалі нездійсненно. Саме тому порівнювати геометричні фігури потрібно геометричними методами. Кількість контрольних вимірювань можна істотно зменшити, якщо скористатися ознаками рівності трикутників.

Подібні трикутники

ЗАДАЧА.  Стовп висотою 15 м закривається монетою діаметром 2 см, якщо тримати її на відстань 70 см від ока. Знайти відстань від стовпа до спостерігача.

ЗАДАЧА.  Тінь, яку відкидає вежа на поверхню землі 9 метрів, тоді, як жердина, заввишки 2 метри відкидає тінь 2,4 метри. Знайти висоту вежі?

ЗАДАЧА.  Висота зображення дерева на задній стінці фотоапарата дорівнює 32 мм. Знайдіть висоту дерева, якщо воно знаходиться на відстані 29 м від об'єктива фотоапарата, а глибина фотокамери 16 см.

ЗАДАЧА.  Знайдіть висоту вежі, якщо відстань від спостерігача до жердини дорівнює 1,5 м, до вежі - 39 м ,висота жердини – 3 м, а зріст спостерігача 1,8 м.

ЗАДАЧА.  Тенісний м’яч подали з висоти 2 м 10 см. Він пролетів над  сіткою, висота якої 90 см. На якій відстані від сітки м'яч впаде на землю, якщо подали його з лінії,  яка знаходиться за 12 м від сітки, і м'яч летить по прямій.

ЗАДАЧА.  Зображення дерева, віддаленого на 60 м від об`єктива фотоапарата , має на плівці висоту 8 мм. Відстань від об’єктива до зображення дорівнює 40 мм. Яка висота дерева?

Коло

Коли і де почали вперше вивчати коло, не відомо, але 4-5 тисяч років тому в Китаї, Індії, Вавілоні та Єгипті вже знали основні його властивості. Римський поет Овідій у поемі «Метаморфози» розповів легенду про винахід циркуля: якось після вдалої риболовлі рибалки зварили юшку і один з них, з’єднавши дві кістки великої рибини, намалював на піску найпрекраснішу з ліній.

У наш час циркулі різного розхилу використовуються в зв’язку з різними потребами техніки, виробництва, будівництва.

Коло – одна з небагатьох ліній, для креслення яких є спеціальні інструменти і пристрої.

Форму кола мають різноманітні речі (або їх деталі) і промислового виробництва, і природного походження.

Термін «радіус» латинською мовою означає «спиця». Вперше цей термін використав французький вчений П’єр Рамус (1515-1572), який загинув 24 серпня 1572р., ставши однією із жертв Варфоломіївської ночі.

Питання про дотичну до кола та про кола, які дотикаються одне до одного, розглядають при демонстрації передавальних механізмів (колеса, паси) або їх зображень.

Можна розглядати, як приклад, наступні питання:

• як летять іскри на шліфувальному крузі під час роботи;
• як летять бризки води з-під коліс машини;
• як розміщені колеса потяга відносно рейок?

Трапеція. Чотирикутники

ЗАДАЧА.  Для садка відвели ділянку землі, яка має форму рівнобічної трапеції, одна з основ на  50 м  більша від кожної сторони, а середня  лінія 90 м. Навколо садка проходить алея шириною 2 м. По обидві сторони від алеї  потрібно посадити дерева на відстані 3 м один від одного. Скільки потрібно для цього дерев?

 ЗАДАЧА.  Для побудови  трампліну поставили балку висотою 10 м, а довжина самого трампліну 13 м. Знайти відстань від балки до початку трампліну, якщо висота трампліну у місці стрибка 2 м?

ЗАДАЧА.  Висоти двох вертикальних стовпів 5 м та 12,5 м відстань між ними 10 м. Знайти найменшу довжину троса яким можна з'єднати верхні кінці стовпів.

ЗАДАЧА.  Ділянка відведена під фруктовий сад має форму трапеції. Дерева розташовані в 5 рядів на однаковій відстані один від одного. У всіх рядах відстань між сусідніми деревами однакова. В одному крайньому ряду 18 дерев, а в другому 26. Скільки дерев в кожному з останніх рядів?

Теорема Піфагора

Теорема Піфагора відіграє особливо важливу роль у курсі геометрії, оскільки за її допомогою виявляють метричні співвідношення між елементами фігур. Ця теорема має велику історію. Напевне відомо, що вже за 3000 років до н.е. єгиптяни знали і використовували при побудовах на земній поверхні той факт, що трикутник з довжинами сторін 3,4,5 – прямокутний.

Вавілонські математики також використовували цю теорему.

Окремі доведення цієї теореми пов’язані з подібністю фігур або з площами, або за допомогою тригонометричних функцій.

Введення тригонометричних функцій було зумовлене потребами астрономії (розвиток якої стимулювався потребами мореплавства і ведення календаря), а також будівельної справи.

ЗАДАЧА. Драбина довжиною 12,5м приставлена до стіни так, що відстань від нижнього кінця драбини до стіни 3,5м. На якій відстані від землі впирається в стіну верхній кінець драбини?

ЗАДАЧА. Вертикальна вежа тримається за допомогою 4 канатів, що кріпляться до неї на відстані 16 м від землі та на відстані 12 м від основи вежі. Скільки метрів канату потрібно, щоб закріпити вежу, якщо на вузли пішло 10м?

ЗАДАЧА. Від  причалу одночасно відплили два пароплава: один на південь зі швидкістю 16 миль за/год, а другий на захід, зі швидкістю 12 миль за/год. Яка відстань буде між пароплавами через 2.5 год.? (1 миля – 1.85 км.)

ЗАДАЧА. Ширина сходинок  в житловому будинку  30 см, а висота 15 см. Знайти довжину  підойму, який містить 20 сходинок?

ЗАДАЧА. До вертикального стовпа в двох місцях, які знаходяться  4 м один від одного, прикріплено 2 троса, другі кінці яких кріпляться до землі. Відстань від основи стовпа до тросів 12 м , довжина меншого троса 12 м. Знайдіть довжину більшого троса.

ЗАДАЧА. Для встановлення вежі телевізійної антени виготовлені троси довжиною 20,2 м , які закріплені до вежі на висоті 1,62 м. На якій відстані від основи вежі потрібно закріпити кінці троса?

ЗАДАЧА. Вертикальна вежа тримається за допомогою 3 канатів, що кріпляться до неї на відстані 10 м  від землі  та до землі на відстані 12 м  від основи  вежі. Скільки  метрів канату потрібно , щоб закріпити вежу?

ЗАДАЧА.  Ескалатор  торгового центру має 23 сходинки. Ширина сходинок 40 см, а висота 20 см. Знайти довжину ескалатора?

Декартові координати на площині

Ідея методу координат з’явилася ще в стародавньому світі. Однією з причин була необхідність орієнтуватися під час плавання у відкритих акваторіях, а не тільки біля берегів. Уже грецький вчений Анаксимандр (VIст. до н.е.) чітко потреби мореплавства, а й перехід до осідлого землеробства вимагали розвитку астрономії. І тут для визначення положення сузір’їв і окремих яскравих зірок, планет корисними виявилися координати. Перше застосування пов’язане з астрономією і географією, з потребою відзначити положення світил на небі та визначених пунктів на поверхні Землі при складанні календаря, зоряних та географічних карт.

Древньогрецький астроном Клавдій Птоломей (І ст.) користувався довготою і широтою як геграфічними координатами. Сліди застосування прямокутної системи координат (палетки) виявлено на стіні однієї з погребальних  камер Стардавнього Єгипту. Прямокутною сіткою користувалися і художники епохи Відродження. Викладання методу координат було вперше опубліковане в «Геометрії» Декарта в 1637 році. Звідси і назва «декартові координати». Терміни «абсциса» і «ордината» походять від латинського перекладу творів Апполонія і були введені в 70-80 роках XVII ст. Г.В.Лейбніцом. Ним же абсциса з ординатою були названі координатами.

Систему координат називають прямокутною, оскільки осі абсцис і ординат перетинаються під прямим кутом.

У системі координат, нанесених на глобус і географічну карту, роль координатних осей відіграють екватор і Грінвіцький меридіан, а координати об’єктів виражаються в градусах.

Існують і інші системи координат, наприклад, полярна система на площині та сферична і циліндрична система координат у просторі.

Тепер люди так привикли до координат, що іноді просто не помічають, як два числа допомагають правильно і швидко орієнтуватися: квиток до театру містить інформацію про певний ряд і номер місця, залізничний квиток – про номер вагона і номер місця, на поштовому конверті записують два трицифрових числа – перше характеризує місто або район, друге – номер відділення зв’язку і т.ін.

Методом координат користуються багато спеціалістів. Наприклад, щоб вказати електрикові, в якому місці стіни треба поставити розетку, досить повідомити її координати: на яких відстанях від лівого краю стіни і від підлоги вона повинна бути.

Щоб вказати комбайнерові, де саме на полі лежить камінь, досить вказати координати цього каменя: на яких відстанях, наприклад, від дороги і від перпендикулярної д неї межі лежить цей камінь.

Широке застосування координати знайшли в будівельній справі, особливо під час монтажних робіт. На заводах працюють координатно-розточувальні верстати.

Без використання методу координат не можна було б успішно розвивати космічну техніку. На основі складних розрахунків космічний корабель запускають так, щоб він після кількох обертів навколо Землі вийшов у той район космічного простору, в якому в цей момент на відстані прямого бачення буде космічна автоматична станція, що рухається навколо нашої планети.

В усіх випадках, коли йдеться про розміщення деякого об’єкта на площині, його задають двома орієнтирами.

Перетворення фігур

Навколишній світ – матеріальний , він перебуваєв неперервному русі, зазнає змін.

Вивчення змін, яких зазнає світ, виявлення відповідних закономірностей неможливе без математики – вона є  зручним інструментом такого вивчення, і без математичної обробки усі висновки будуть неповними. Шкільна програма передбачає грунтовне вивчення геометричних перетворень.

Деякі геометричні перетворення були відомі ще в стародавні часи. У Греції  осьовою симетрією  цікавилися в школі Піфагора, велику увагу приділяв їм Аполлоній Пергський (ІІІ ст. до н.е.). Докладно вивчав геометричні перетворення і створив їх загальну теорію видатний математик Леонард Ейлер (1707-1783).

Види геометричних перетворень:  рух, перетворення подібності.

Симетрія відносно точки, симетрія відносно прямої є рухом.

Ще одним видом руху є поворот навколо точки. Здійснюючи поворот навколо точки, розрізняють напрям повороту за рухом годинникової стрілки і проти її руху. Цей напрям іноді буває дуже істотним. Зокрема, у техніці розрізняють праву і ліву нарізку (якщо нарізки не збігаються, то болт і гайка одного діаметра не сполучаються). В певний період було виявлено, що є молюски одного й того самого виду, які, залежно від температури води, що їх оточує, відрізняються напрямом закруту черепашок. Грунтуючись на цьому, учені за рештками молюсків, що жили 10-20 мільйонів років тому, склали перші кліматичні карти Землі.

Рівність фігур не вичерпує потреб суспільного виробницва. Легко зрозуміти, що коли б карти місцевості були виготовлені в натуральну величину, ними не можна було б користуватися. У натуральну величину не можна виготовити і карти зоряного неба чи схематичні зображення процесів мікросвіту.

Неможливо обійтися без креслень і планів, поданих у деякому масштабі, при виготовлені деталей, виконанні складальних і будівельно-монтажних робіт. У всіх цих випадках йдеться про фігури, які мають таку саму форму, що й оригінал, але відрізняються від нього розмірами лінійних елементів, тобто про подібні фігури.

Подібність фігур широко застосовується в техніці, зокрема у технічному моделюванні. Так, перед початком виготовлення літака певної констукції виготовляється його модель. Її закріплюють і по спеціальній аеродинамічній трубі з великою швидкістю проноситься підфарбоване повітря. Вимірюючи швидкість руху повітря і вплив цього руху на модель, роблять висновки про прийнятність проекту або про потребу внести в нього певні зміни, про можливості запропонованого літака. Також, жодного проекту гідроелектростанції без попередньої перевірки на моделях не затверджують.

Паралельне перенесення можна проілюструвати практичними прикладами: рух автомобіля на прямолінійній ділянці шляху, переміщення деталей на конвейєрі.

Розв’язування трикутників

Співвідношення між сторонами і кутами прямокутного трикутника дають можливість розв’язувати вправи на визначення висоти предмета або відстаней між пунктами земної поверхні.

ЗАДАЧА. Автомобіль піднімається по шоссе вверх вздовж моря під кутом 15⁰ і проїздить 500 метрів. Яку відстань пройде пішохід, рухаючись пішки берегом моря?

ЗАДАЧА. Висока радіовежа закріплена тросами. Яку довжину має трос, якщо точка А знаходиться на відстані 75 м від основи вежі, і трос закріплено під кутом 59⁰ до землі?

ЗАДАЧА. Якої довжини має бути пожежна драбина, щоб по ній можна було піднятися на дах будинку заввишки 9 м, якщо ставити її під кутом 70⁰ до поверхні землі?

ЗАДАЧА. Проїхавши від старту прямолінійною ділянкою шоссе 300 м, велосипедист опинився на 11 м вище, ніж точка старту. Знайдіть кут підйому шоссе на цій ділянці.

ЗАДАЧА. Розвідний міст підняли під кутом 32⁰ на висоту 40 метрів. Знайти довжину моста?

ЗАДАЧА. Сашко, дивлячись на дерево, бачить верхівку під кутом 32⁰. Зріст Сашка 1,6 м, відстань до дерева 8 м. Знайдіть висоту дерева.

ЗАДАЧА. Під яким кутом падає на землю сонячний промінь, якщо вертикальна жердина, довжина якої становить 1,5 м, відкидає тінь завдовжки 0,7 м?

Проте на практиці зустрічається значно більше задач, пов’язаних не з прямокутними, а з косокутними трикутниками, коли визначення лінійних та кутових елементів трикутника ускладнюється. Розуміючи це, вавілонські математики вже 35-40 століть тому розбивали висотою гострокутний трикутник на два прямокутних. У процесі цих пошуків було відкрито  багато властивостей трикутника та співвідношень між його елементами. Серед них дуже корисними виявилися теореми синусів та косинусів.

Теорема синусів стала відомою пізніше, ніж теорема косинусів. Потреби астрономії і мореплавства привели давньогрецьких математиків до вивчення питання про співвідношення між дугами кола і хордами, які ці дуги стягують.

 

Многокутники

Правильні многокутники зустрічаються дуже часто як форми будівельних деталей, промислових виробів. Найбільш відомі з них – правильний трикутник і квадрат. Як показують археологічні розкопки, орнаменти з використанням рівностороннього трикутника і квадрата були поширені вже 25000 років тому.

ЗАДАЧА. Як скласти паркет із:

• правильних восьмикутників і квадратів;
• правильних дванадцятикутників і трикутників;

З яких правильних многокутників одного виду можна скласти паркет?

ЗАДАЧА. Обчислити,який розмір отвору ω повинен мати ключ для правильної шестигранної гайки, якщо ширина грані гайки а=2,5см. Величина зазору між гранями гайки і ключа дорівнює 0,5мм.

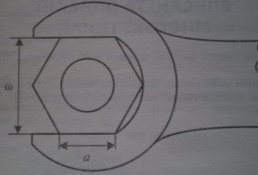
ЗАДАЧА. Найпростіше мансардне покриття утворює у вертикальному розрізі половину правильного восьмикутника. Знайти ширину перекриття ВД, сторону восьмикутника і висоту мансардної кімнати АВДЕ. Дано: АЕ=6см.

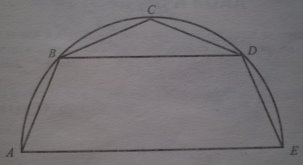
ЗАДАЧА. Сім’я вирішила вистелити підлогу кімнати розміром 6м х 4м плитками правильної шестикутної форми.

1. Скільки потрібно купити таких плиток, якщо сторона плитки 20см.
2. Скільки коштів витратить сімя , якщо одна плитка коштує 28грн?

Площі многокутників

ЗАДАЧА. Підлогу прямокутного фойє, площа якого 14,6х8,4м, необхідно встелити керамічними плитками двох різних кольорів (плиток кожного кольору - порівну). Скільки необхідно плиток кожного кольору, якщо плитка має форму правильного шестикутника зі стороною 10см?

ЗАДАЧА. Підлогу прямокутного фойє навчального закладу, розмір якого 10м х 30м, потрібно покрити керамічною плиткою квадратної форми. Плитка розміром 33см х 33см коштує по 18грн за штуку, а розміром 40см х 40см – по 27 горн за штуку.

1. Скільки потрібно меншої плитки, щоб покрити підлогу фойє і скільки вона буде коштувати?
2. Скільки потрібно більшої  плитки, щоб покрити підлогу фойє і скільки вона буде коштувати?
3. Яку плитку вигідніше купити?

ЗАДАЧА. Стіна актової зали довжиною 8,25м і висотою 4,32м має три вікна розміром 2,2м х 1,2м кожне.

1. Знайти площу поверхні стіни.
2. Скільки рулонів шпалер потрібно для обклеювання стіни, якщо рулон має ширину 0,52м і довжину 10м? На підгін малюнка витрачається 5% шпалер.

Вписані та описані многокутники. Довжина кола.

ЗАДАЧА. По колу потрібно розмістити центри отворів для 15 болтів так, щоб відстань між центрами отворів дорівнювало 30 мм. Знайдіть довжину радіуса кола.

ЗАДАЧА. Кути квадратного залізного листа зі стороною а зрізані так, що утворився правильний восьмикутник. Знайти сторону восьмикутника.

ЗАДАЧА. Кінець гвинта газової засувки має правильну тригранну форму. Який найбільший розмір може мати основа кожної грані, якщо циліндрична частина гвинта має діаметр 2см?

ЗАДАЧА. Шків має в діаметрі 1,4м і робить 80 обертів за хвилину. Визначити швидкість точки, що лежить на колі шківа.

ЗАДАЧА. Обід шківа дорівнює 540мм, пас дотикається до шківа по дузі АВ завдовжки 200мм. Визначити кут α  обхвату шківа пасом.

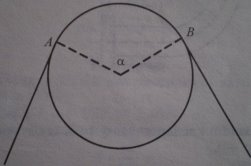
ЗАДАЧА. Для дуг заокруглень залізничної колії не допускаються радіуси кривизни, менші за 600м. Обчислити межу допустимих значень довжини х стрілки дуги заокруглення залізничної колії, якщо ця дуга менша за 180⁰ і її хорда дорівнює 156м. (Стрілкою дуги називають частину діаметра, перпендикулярного до хорди, що стягує хорду і лежить між дугою та хордою)

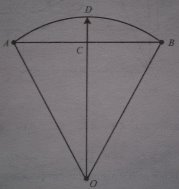
ЗАДАЧА. Дано схему ділянки спряження двох паралельних залізничних колій. Знайти довжину ділянки спряження l. Визначити довжини рейок ділянки спряження за розмірами на рисунку.

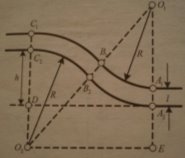
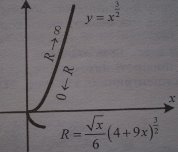
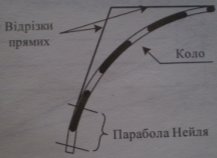
Відомо , що у місцях спряження і на поворотах залізнична колія складається з прямолінійних ділянок і дуг кіл.

Насправді геометрія залізничних колій на поворотах складніша. Якщо залишити стики прямих і кіл неплавними при переході від прямолінійної ділянки до криволінійної і навпаки, то вагони поїзда завдаватимуть ударів, від яких швидко зношуватимуться рейки й колеса, розхитуватимуться кріплення вагонів.

Щоб уникнути цих небезпечних чинників, у точках спряження прямолінійних ділянок залізничних колій із криволінійними роблять так звані перехідні ділянки по півкубічній параболі, так званій параболі Нейля, кривизна якої набуває значень від нуля до нескінченності. Магістраль спочатку трасується відрізками прямих ліній, потім утворені кути заокруглюються колами. Відрізок параболи Нейля обирають так, щоб на одному кінці параболи радіус її кривизни набував значення, яке дорівнюватиме радіусу заокруглюючого кола, а на другому – дуже великого значення порядку 2-5тис.м.

Перехідні ділянки роблять ще й тому, що на заокругленнях зовнішня рейка має бути вкладена трохи вище від внутрішньої, аби врівноважити відцентрову силу під час руху по кривій. Зовнішня рейка піднімається над внутрішньою – міліметр підйому на кожен погонний метр шляху. За технічними нормами це перевищення не має бути більшим за 125мм.

ЗАДАЧА. Повороти на дорогах завжди вимагають особливої уваги. Автомашина, яка проходить поворот, займає на проїжджій частині більшу ширину, ніж на прямій ділянці дороги. Цим зумовлено розширення дороги з однією смугою на повороті радіуса R (R- радіус зовнішнього краю дороги).

Обчислити величину h розширення дороги для автомобіля, поздовжня база (відстань між осями) якого дорівнює  l.

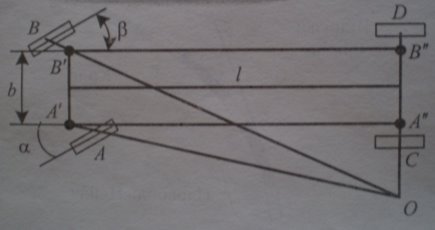
Площі фігур

ЗАДАЧА. На стругальному верстаті при кожному проходженні різця вздовж оброблювальної плити зрізується вузька смужка металу, після чого різець повертається назад. У кінці зворотного ходу, щоб різець зміг зрізати наступну смужку металу, плита переміщується в поперечному напрямі на величину подачі, а вершина  різця з точки А переходить у точку В (рисунок). Внаслідок цього поперечний переріз поверхні плити, обробленої на стругальному верстаті має убчасту форму. Визначити висоту  h нерівностей поверхні плити , яка обробляється, якщо радіус гострого краю різця дорівнює R, а подача різця -s. Дослідивши формулу, що визначає h через s і R , знайдемо, як змінюється h  зі зміною s і R .  

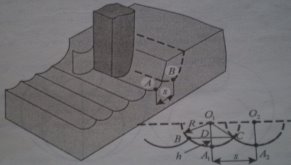
ЗАДАЧА. Слюсар помітив, що контролер перевіряє точність обробки отвору діаметром 3см, опускаючи в нього 2 калібри-пробки діаметром 2 і 1 см. Тоді слюсар запропонував для підвищення точності контролю форми отвору разом із цими двома калібрами опускати ще 2, які мають щільно прилягати до стінки і до обох перших калібрів.

При цьому навіть розрахував (обійшовшись без тригонометрії) діаметри цих двох додаткових калібрів (зрозуміло, що вони мають бути однаковими). Визначити діаметри калібрів, запропоновані слюсарем.

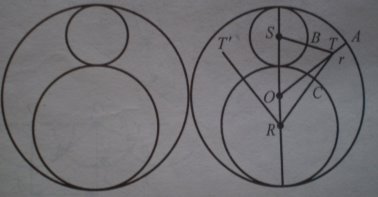
ЗАДАЧА. Щоб розточити на координатно-розточувальному верстаті отвори О₁, О₂,…, О_п, треба знати координати їх центрів.

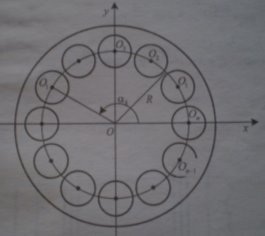
Знаючи, що центри п отворів О₁, О₂,…, О_п   розміщені по колу радіуса R і однаково віддалені один від одного, визначити їх координати у введеній на рисунку системі координат.

ЗАДАЧА. Визначити площу вікна, яке має форму прямокутника, закінченого вгорі дугою кола в 60⁰; висота вікна від середини дуги до основи дорівнює 2,4м, а ширина його – 1,6м.

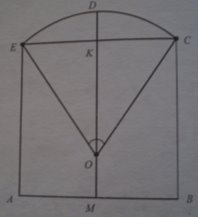
Вступ до стереометрії

Виникнення геометричних знань пов’язане з практичною діяльністю людини. Це відобразилося у назвах більшості геометричних фігур. Наприклад, “linum” (лат.) – лляна нитка, “trapezion” (грецьк.) – столик, “stereo” – простір , “konos” – соснова шишка, “geo” – земля, “metreo” (грецьк.) – вимірюю.

Перші геометричні факти знаходимо у вавілонських клинописних таблицях і єгипетських  їх центрівпапірусах (ІІІ тисячоліття до н.е.)

У ІІІ столітті до н.е. давньогрецький учений Евклід написав працю «Начала», в якій узагальнив накопичені до того часу геометричні знання. Перші чотири і шоста книги присвячені планіметрії, три останні – стереометрії. Написані вони були настільки добре, що протягом двох тисяч років викладання геометрії велося за перекладами книг Евкліда.

Лише в ХІХст. завдяки працям російського математика М.І.Лобачевського та угорського математика Н.Больяї було встановлено існування нескінченно складніших геометричних просторів , для яких не виконується тільки одна –єдина аксіома паралельних прямих, проведених через дану точку до даної прямої більше однієї. Сума кутів трикутників на такій поверхні не дорівнює 180⁰.

Можливо, просторові, що має багато галактик, краще відповідає геометрія Лобачевського. Проте для нашої повсякденної діяльності ми можемо продовжувати користуватися «старою», добре відомою і, головне, найпростішою  з усіх геометрій – Евклідовою.

Виникнувши із потреб практики, постійно розвиваючись, геометрія є однією з найважливіших наук для описання  навколишнього світу. Знайомство із геометрією простору вкрай потрібно людині для її загального розвитку і професійного становлення.

Геометрія простору – це математична наука про просторові геометричні фігури і відношення між ними, а також про їхні властивості. Називають її стереометрією. Виникнувши із практики, постійно звертаючись до неї в процесі  свого розвитку, геометрія стала однією з найважливіших математичних наук для опису навколишнього світу. Геометричні фігури є абстракціями об’єктів реального світу , в яких відображається лише їхня форма і розміри. Інакше кажучи, геометричні фігури є математичними моделями об’єктів навколишнього середовища.

Так, наприклад, точку у просторі можна розглядати як математичну ідеалізацію реальних об’єктів – зірок на небі, сліду голки на папері чи тканині, кінчика олівця тощо. Точка в геометрії немає звичних розмірів. Вона застосовується для моделювання різних фізичних тіл маленьких розмірів. Безумовно, маленьких відносно інших тіл (у певних випадках футбольний м’яч можна вважати точкою на футбольному полі).

Один і той самий предмет може моделюватися різними фігурами в залежності від мети, якою керуються. Можна вважати, що кришка даного стола має форму  прямокутного паралелепіпеда, якщо нам необхідно знайти її масу, користуючись густиною деревини. Але саму кришку можна уявляти у формі прямокутника, якщо нам необхідно пошити скатертину.

Поняття точки, прямої, площини, відрізка тощо відносяться до основних у стереометрії, бо з них починається її побудова. Головною метою стереометрії є вивчення суто просторових фігур. Тому , щоб зробити побудову стереометрії змістовнішою, використовують деякі просторові фігури – куб, паралелепіпед, піраміду, кулю та ін..

          Знання з теми   «Вступ до стереометрії» необхідні учням для  просторової розмітки поверхонь, розмітки і читанні електричних схем, виконання креслень моделей одягу, вивчення схем кінематичних схем.

          Згідно програми учні повинні вміти:

• наносити паралельні лінії при розмітці,перевіряти горизонтальність поверхонь, деталей, правильність  розміщення матеріалів та інструментів при виконанні  робіт;
•    використовувати  властивості прямих і площин, паралельність при виконанні розмітки трас відкритих електропроводок, встановленні вимикачів, розеток, світильників, при виконанні креслень;

- наносити перпендикулярні лінії при розмітці, перевіряти  вертикальність,  правильність розміщення матеріалів та інструментів при виконанні робіт, визначати правильне розміщення поверхонь і інструментів у просторі;

-  розв’язувати виробничі задачі на обчислення площі основи, бічної та повної поверхні деталей та конструкцій (споруд), які мають форму многогранників, робити розрахунок матеріалів при виконанні робіт,  визначати  кути між поверхнями, інструментами.

Аксіоми стереометрії

Предмети, що нас оточують, деталі машин і механізмів мають форму просторових фігур або їх комбінацій.

Уявлення про точки дають предмети, розмірами яких за даних умов можна знехтувати. Наприклад, навіть зорі на астрономічних картах розглядають як точки. Про лінії говоримо тоді, коли істотною є протяжність в одному напрямі (траєкторія руху літака). Границя тіла (уявити можна шар фарби, яким воно покрите) дає уявлення про геометричну поверхню.

Площина необмежена. Проте зображають обмежену частину її у вигляді паралелограма. Це відповідає вигляду поверхні письмового стола, книжки, шибки, якщо дивитися на ці предмети під кутом і з достатньої відстані.

Прагнення максимально наблизити оброблювальну поверхню того чи іншого виробу до частини ідеальної площини можна спостерігати у роботі різних фахівців. Наприклад, столяр послідовно обробляє дошку шерхебелем , рубанком, фуганком; шпаклює, шліфує наждачним папером і покриває лаком.

Аксіоми стереометрії можна ілюструвати прикладами з життя.

С1. Уявіть собі спокійну поверхню води. Звичайно , є молекули, що належать цій поверхні і що не належать їй, перебуваючи у повітрі, або в товщі води.

Аксіома С3 дає можливість вирішити питання стійкого кріплення чи розташування предметів на одній площині. У житті це виражається терміном «предмет не хитається». При цьому використовуються не тільки дві  прямі, що перетинаються. Як стійко кріпляться столики у залізничних вагонах? (Через частину прямої – завіси і точку - підпору). А ще столики, стільці, особливо штативи геодезичних приладів часто бувають не «чотириногі», а – «триногі». Офіціанти часто підтримують піднос трьома пальцями. Ці приклади демонструють твердження про існування та єдність площини, яка проведена через пряму і точку і через три точки.

ЗАДАЧА. Як повинен натягнути дві нитки столяр, щоб перевірити, чи лежать кінці чотирьох ніжок стола в одній площині?

ЗАДАЧА. Яке геометричне твердження ілюструють такі життєві ситуації:

А) Кріплення дверей в площині стіни за допомогою замка.

Б) Стіл із чотирма ніжками, який стоїть на рівній підлозі, інколи хитається, я стіл із трьома ніжками завжди стоїть стійко.

В) мотоцикл, спираючись тільки на два колеса , стояти не може, а якщо додати ніжку-опору , то може.

ЗАДАЧА. Є два твердження: а) пряма, яка проходить через дві різні точки площини, лежить у цій площині; б) через дві  прямі, які перетинаються , можна провести одну площину. Співставте  умови тверджень із початковими діями операції перевірки якості обробленої поверхні штукатурами при роботі із шпателем і правилом; столярами при роботі з контрольною лінійкою. Зробіть висновок відносно правильності використаного методу перевірки. Поясніть свою відповідь відповідними операціями з інструментами і пристроями.

ЗАДАЧА. Якщо тільки деякі  точки дроту дотикаються до плоскої поверхні ковадла, дріт «не прямий». Чому?

Щоб вирівняти його, б’ють молотком, як показано на рисунку. При цьому дріт повертають. Навіщо?

 

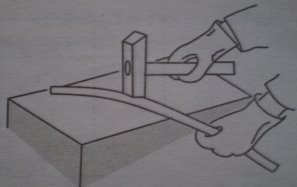
Взаємне розміщення двох прямих у просторі

На площині дві прямі можуть збігатися, перетинатися або бути паралельними. Ілюстрацією цього можуть бути траєкторії руху двох пароплавів.

Перехід від площини до простору збільшує кількість варіантів взаємного розміщення двох прямих. Як приклад, можна уявити траєкторію руху двох літаків, які летять на різних висотах, і один із них рухається з півночі на південь, а другий – із заходу на схід.

Як вони розміщені?

Яскравою ілюстрацією можливостей взаємного розміщення двох прямих є розміщення поперечних рей на корабельних щоглах.

ЗАДАЧА. Як розташовані осі залізничних вагонів між собою; відносно рейок?

Розглядаючи прямі у просторі як геометричні образи траєкторій прямолінійного руху, можна описати можливі варіанти взаємного розміщення двох прямих у просторі.

Усі ребра прямозубої  циліндричної шестерні лежать на паралельних прямих , але не належать  одній площині.

Прямі можуть не мати спільних точок. Проте назвати їх паралельними можна не завжди. Розгляд траєкторії польоту літаків, як і багато інших подібних прикладів (розміщення тунелів метро, лінії електропередач, що перехрещуються ) наводить на думку, що йдеться про два принципово різних способи розміщення прямих. ПРЯМІ – паралельні і мимобіжні.

На рисунку зображено десятки пар матеріальних моделей мимобіжних прямих.

Паралельність прямих і площин

Навколо себе ми бачимо безліч прикладів, які ілюструють взаємне розміщення прямих і площин(взаємне розміщення стін, стелі, підлоги в кімнаті та лінії їх перетину, перекладини футбольних воріт і поверхні землі, ручки й аркушу паперу)

 

Теорему  про взаємне розміщення прямої і площини може бути проілюстрована у житті на таких прикладах: за допомогою якісної лінійки перевіряють, чи добре оброблено плоску поверхню виробу і , навпаки, правильність виготовлення лінійки – за допомогою відполірованої плоскої плити. Цьому геометричному твердженню відповідає спосіб вирівнювання дроту, цвяха на кувалді.

В оточуючій дійсності можна дуже часто зустріти приклади застосування паралельності ділянок прямих чи прямої і площини. Паралельні всі поздовжні ребра брусів, дошок, ребра різноманітної прокатної продукції (рейок, балок), силові лінії між паралельними гранями магніту (N-S). Муляри кладуть стіни під шнур, натягнутий паралельно до стіни. Труби опалення в будинках найчастіше паралельні до стін, ділянки ліній електропередач – до поверхні землі. Горизонтальні планки мотовила зернозбирального комбайна хоч і змінюють свої положення під час роботи, весь час залишаються паралельними площині поля.

ЗАДАЧА. Покрівля і підошва вугільного пласта та й самі пласти на великих площах розміщені паралельно. Звичайно, розробляє одночасно кілька таких пластів і через один ствол піднімає нагора вугілля з двох або трьох горизонтів. Створіть математичну модель та схематичний малюнок описаного технологічного процесу.

Ще з давніх - давен людина завжди прагнула мати дах над головою. Спочатку це були печери, потім невеликі хатки. І ще не знаючи правил і норм будівництва, люди інтуїтивно розуміли, що зручно коли стеля паралельна підлозі; що стіни, як правило, перпендикулярні площині підлоги і таке інше. А далі,з розвитком науки і техніки, вони отримали можливість мати сучасне і зручне житло.

Без знань математики і без вміння використовувати їх на практиці сучасних споруд не побудуєш. Математика тісно пов’язана з різними галузями будівництва (починаючи від проектування і завершуючи безпосередньо спорудженням об’єктів).

ЗАДАЧА.(для архітекторів) При проектуванні покрівлі необхідно зробити укріплення стропил. При цьому треба визначити, чи буде стропило, яке перетинає два інших, паралельних між собою, лежати з ними в одній площині.

ЗАДАЧА (для конструкторів).Покрівля складається з двох паралельних площин. Знайти кут нахилу стропила похилої покрівлі до площини підлоги горища, якщо довжина стропила 4м, а висота горища 2м.

ЗАДАЧА (визначення кошторису). Підрахувати вартість паркетної підлоги на 1-му, 2-му і мансардному поверхах, якщо загальна площа 1-го поверху 1500м² і вартість 1м² паркету 300гр. площа підлоги кожного з трьох приміщень однакова.

ЗАДАЧА. На лісопильних рамах для поздовжнього розпилювання колод їх часто розпилюють на квадратний брус і чотири дошки., при чому  товщина дошки становить 0,1d. Скільки пил при цьому встановлюють і як? Якої товщини вийде брус і дошки з колоди діаметром 30см?

Паралельність площин

Наочне уявлення про розміщення двох площин дає моделювання за допомогою площин поверхонь суміжних стін,стелі і підлоги, двоярусних ліжок, кілька  скріплених аркушів книги.

Пряма,  проведена в грані бруска за допомогою рейсмуса, паралельна площинам трьох граней.

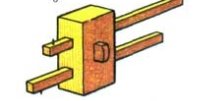
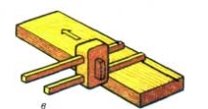
Моделі паралельних плоі балщин: підлога і стеля кімнати, підлога і поверхня столу, шибки подвійних вікон. Паралельні шари фанери, протилежні грані цеглини, швелери, двотаврові балки, пилки пилорами.

Перетворення фігур у просторі

Якщо кожну точку фігури замістити яким-небудь чином, то ми дістанемо фігуру , утворену перетворенням даної. Весь світ у русі і розвитку зазнає щомиттєвих перетворень. Математика прагне їх описати  і вивчити властивості з тим, щоб знову застосувати при вивченні явищ світу.

Як приклад, можна розглянути два перетворення фігури:

А) від доменної печі подали болванку на прокатний стан і виготовили стальний лист;

Б) стальний лист відтранспортували зі складу в цех і склепали з нього трубу.

У кожному прикладі описано по два перетворення , які по-різному впливають на точки фігури. Чим же вони відрізняються? Отже, всі перетворення поділяються на ті, що зберігають відстані між точками фігури і ті, що не зберігають. Причому складні перетворення часто вдається розкласти на кілька простих. Наприклад, рух автомобільного колеса можна розкласти на поступальний разом з автомобілем зі швидкістю v та обертальний з певною кутовою швидкістю.

У результаті матимемо таку класифікацію перетворень фігур:

1. Ті, що зберігають відстані між точками фігури – рухи (симетрія відносно точки; симетрія відносно прямої; симетрія відносно площини; паралельне перенесення; поворот);
2. Ті, що не зберігають відстані між точками фігури (подібність (гомотетія); деформації, афінні перетворення (проектування)).

Прикладами паралельного перенесення в просторі є : прямолінійний поступальний рух транспорту; зведення багатоквартирного будинку; укладання рейок, настилання підлоги паркетом, тротуару – однаковими плитами; робота верстатів з ЧПУ, коли деталь або інструмент переміщується по напрямним верстата.

Паралельне проектування

Зобразити тривимірний об’єкт на плоскому кресленні з абсолютною точністю неможливо. Однак за допомогою плоского рисунку можна одержати досить чітке уявлення про окремі властивості просторової фігури. Щоб плоскі рисунки давали якомога чіткіше уявлення про властивості тієї чи іншої просторової фігури, необхідно знати правила зображення просторових фігур на площині.  Йдеться про побудову таких зображень, які б відображали властивості оригіналу й уможливлювали достатньо просте, наочне і однозначне ознайомлення з ним.

Наочний приклад паралельного проектування – тінь предмета на плоскій поверхні. Спосіб побудови зображення фігури підказують нам тіні, що падають від її просторової моделі. При цьому можливі два випадки. У першому з них промені виходять з точкового джерела світла (лампи, ліхтаря), розміщеного поблизу моделі. Цій ситуації відповідає центральне проектування.

За його законами формується  зображення предметів на сітківці ока. Проте центральне проектування спотворює одне з основних відношень геометрії – паралельність(нам здається, що залізничні колії на горизонті збігаються).

Крім того, створення такого зображення є досить складною справою.

Інший спосіб зображення просторових фігур пов'язаний з освітленням моделі паралельними променями. Такими можна вважати сонячні промені. Через суттєву віддаленість Землі від Сонця можна вважати сонячні промені паралельними.

Відповідний метод відображення називається методом паралельного проектування.

Певні властивості паралельного проектування (властивість проекції паралельних прямих) можна обґрунтувати відомим фактом : сонячні тіні від паралельних стовпів – паралельні.

При паралельному проектуванні  довжини відрізків змінюються. Тінь від вертикального стовпа може бути і коротшою, і довшою від стовпа, залежно від положення Сонця над горизонтом. Разом з тим, можна спостерігати пропорційну залежність між довжинами паралельних стовпів і їхніх тіней.

Говорячи про паралельні проекції основних плоских фігур, не можна обминути кола. Уявлення про форму паралельної проекції круга і відповідного йому кола можна отримати, експериментуючи з тінню картонного круга. Цей експеримент можна змоделювати за допомогою циліндричної склянки з рідиною. Якщо ї нахилити, то поверхню рідини можна розглядати як паралельну проекцію дна склянки, яке має форму круга. Зрозуміло, що напрям проектування паралельний осі симетрії склянки, а площина проекції – площина поверхні рідини.

                

Таку саму форму мають ковбасні зрізи. Їх можна вважати паралельними проекціями поперечних перерізів (кругів) уздовж ковбасного батона.

           

Ці міркування дозволяють сформулювати означення. ПАРАЛЕЛЬНА проекція кола називається еліпсом.

На площині еліпс зображають у вигляді овала. Ця фігура відіграє помітну роль у математиці та природознавстві. Досить сказати, що траєкторія руху Землі та інших планет навколо Сонця – еліптичні.

Зображення фігур у стереометрії

При вивченні питання про зображення фігур у стереометрії основну увагу зосереджують на  зображенні плоских фігур. І це зрозуміло, оскільки дивлячись на реальний фізичний об’єкт (будинок, гральний кубик, книжку, та ін..) , ми бачимо поверхню, яка у багатьох випадках  складається з плоских частин.

  

На рисунках та технічних кресленнях передусім намагаються зобразити поверхню об’єкта, а наш життєвий досвід дає змогу за деталями поверхні побачити предмет у цілому.

За геометричну основу зображення беруть паралельне проектування.

Перпендикулярність прямих і площин

Численні застосування геометрії пов’язані, насамперед, з вимірюванням геометричних величин (відстаней, кутів). Предметом багатьох вимірювань є прямі та площини, які перетинаються. Тому необхідно більш детально дослідити взаємне розміщення прямих і площин, виявити величини, які характеризують це розміщення.

Окремим випадком розміщення прямої та площини, що мають одну спільну точку, є перпендикулярність, яка моделює відношення вертикальності між фізичними тілами та інші подібні відношення (цвях, забитий у стіну). Скориставшись поняттям перпендикулярності, ми зможемо вимірювати відстань від точки до площини, від прямої до паралельної їй площини, відстань між паралельними площинами. На цих вимірюваннях ґрунтується вимірювання відстані між довільними реальними об’єктами.

Не менш важливим є введення кількісних характеристик взаємного розміщення прямих і площин, що перетинаються, - кута між прямою і площиною, кута між площинами. Ці поняття споріднені з планіметричним поняттям кута між прямими.

Взаємне розміщення прямої і площини моделює відношення вертикальності.

Можна навести багато прикладів взаємного розміщення фізичних об’єктів, які характеризуються математичним поняттям перпендикулярності прямої і площини: вертикальна колона перпендикулярна до поверхні землі, ніжки стола перпендикулярні до підлоги, шнур на якому висить лампа – до стелі, траєкторія тіла, що вільно падає, - до поверхні Землі.

 

Заводські димові труби, телевізійні вежі, стовпи, нафтові свердловини і шахтні стволи, колодязі роблять перпендикулярними до площини горизонту. Голка швейної машини, свердло в свердлильному верстаті переміщують по прямій, перпендикулярній до площини станини. Бурильні установки, підйомні крани під час роботи встановлюють перпендикулярно до площини горизонту. Всі кріпильні болти, цвяхи перпендикулярні до площини кріплення. Перпендикулярно до площини горизонту запускають космічні кораблі ( згодом ракета-носій лягає на курс).

У практичній діяльності вертикальність веж, опор, стовпів та інших конструкцій теж звіряють по їхній вертикальності двом напрямам. Вертикальність корінця напіврозкритої книги, що стоїть на столі, забезпечує його перпендикулярність до двох країв обкладинки, на які спирається книга і які лежать у площині стола.

Будуючи багатоповерховий будинок , спочатку зводять каркас, в якому кожна колона перпендикулярна до площини горизонту і до кожної горизонтальної балки.

У тому, що перпендикулярності даної прямої до однієї прямої площини не вистачає для її перпендикулярності до площини, можна переконатися за допомогою наступного прикладу. Ручка швабри перпендикулярна до перекладини, яка лежить на підлозі, але цього не достатньо, щоб ручка була розміщена вертикально. Але якщо ручку обертати навколо перекладини, то можна знайти положення, коли вона буде вертикальною. Це якраз буде тоді, коли вона буде перпендикулярною ще до одного напряму на підлозі.

Ознаку перпендикулярності прямої і площини можна використати для побудови вертикальних конструкцій.

ЗАДАЧА. Встановити щоглу вертикально за допомогою розтяжок, закріплених на щоглі на певному рівні.

= Зазвичай для встановлення щогли досить мати чотири розтяжки однакової довжини. Зрозуміло, що довжина розтяжок повинна бути більшою, ніж віддаль від землі до місця їхнього закріплення на щоглі. Розміщують основу щогли у даній точці на поверхні землі, закріплюють вільні кінці двох розтяжок у відповідних точках, які розміщені на однаковій відстані від основи і лежать на прямій, що проходить через основу. Це забезпечує перпендикулярність щогли до цієї прямої. За допомогою двох інших розтяжок щоглу піднімають. Потім фіксують те положення щогли, в якому вільні кінці розтяжок закріплюються у точках, центрально - симетричних відносно точки – основи щогли. Щогла стоїть вертикально.

Існують інші способи встановлення щогли. Наприклад, можна зменшити кількість розтяжок, брати розтяжки різної довжини, закріплювати їх на різних рівнях щогли. Але усі ці випадки вимагають забезпечення стійкості вертикальності щогли у двох напрямах.

Розв’язування завдання, сформульованого у задачі, звелося з позицій геометрії до побудови прямої , яка проходить через точку площини перпендикулярно до цієї площини.

ЗАДАЧА. Чи достатньо однієї пари розтяжок для забезпечення вертикальності щогли?

ЗАДАЧА При поперечному розпилюванні дерев’яного бруса тесля тримає пилку так, щоб можна було бачити дві суміжні грані бруса. З якою метою він це робить?

ЗАДАЧА Як перевірити перпендикулярність осі свердла до площини стола, на якому закріплюють деталь?

ЗАДАЧА Кімната має довжину 6м, ширину 5м і висоту 3м. Знайдіть відстань від світильника, який розміщений в центрі стелі, до нижніх кутів кімнати.

Перпендикуляр і похила

У планіметрії вимірювання відстаней між точкою і прямою або між паралельними прямими пов’язане з порівнянням довжин похилих і перпендикулярів. Аналогічні поняття розглядаються і у просторі.

У житті маємо змогу спостерігати, як кріпляться телевізійні вишки і антени, щогли вітрильників з допомогою тросів-відтяжок. Це наочні приклади перпендикулярів і похилих до площини землі, палуби.

Властивість перпендикуляра до площини і властивість похилих і їхніх проекцій можна вважати наслідками теореми Піфагора. Їх легко можна проілюструвати прикладами з навколишнього середовища.

Вертикальна підпірка до стовпа з ліхтарем менша від частини стовпа від землі до місця кріплення підпірки (перпендикуляр менший від похилої).

    

При запуску повітряного змія чим більше відмотаєш мотузки, тим далі будеш знаходитися від місця, над яким знаходиться змій(більшій похилій відповідає більша проекція).

Під час катання на каруселі всі знаходяться на однаковій відстані від стовпа, до якого кріпляться кабінки (рівні похилі мають рівні проекції).

Властивості перпендикуляра і похилої широко застосовуються в стереометрії для встановлення взаємного розміщення геометричних фігур, вимірювання відстаней. Варто звернути увагу і на зручність користування термінологією, що сформувалася при цьому.

ЗАДАЧА. Радіощогла висотою 30м кріпиться трьома тросами на висоті 16м від землі. Місця кріплення знаходяться на відстані 12м від основи щогли. Знайти довжину тросів (на кріплення йде 5% матеріалу).

ЗАДАЧА. Знайти відстань від вершини башти до дороги, якщо відомі висота башти h  і відстань a  від дороги до підніжжя башти.

ЗАДАЧА. Над квадратною будівлею розміром 8м на 8м потрібно виготовити дах, найвища точка якого знаходиться на висоті 2м над основою даху. Які найдовші крокви потрібні для цього? (на практиці додають 30см, що не затікало).

Даний приклад – це підтвердження  використання при вимірюванні відстаней і встановленні перпендикулярності прямих у просторі ( теорема про три перпендикуляри) .

У практиці будівництва довжину лінії на площині вимірюють за допомогою стрічки, дроту, рулетки. Часто виміри необхідно виконувати на нахиленій площині, при цьому визначають величину проекції цієї лінії на горизонтальній поверхні. Для цього в одержане значення вводять поправку на нахил лінії ∆l_к м:   ,

де h – перевищення одного кінця стрічки щодо другого;

l –довжина вимірювальної лінії.

ЗАДАЧА. Довжина вимірювальної нахиленої лінії -100м, перевищення однієї точки над другою -3,5м. Обчисліть поправку ∆l_к та горизонтальне значення лінії.

Розв’язок подібних задач вчить майбутніх будівельників не сприймати все в готовому вигляді, а побачити в кожній формулі глибокий зміст, уміти вивести її, виховується творчий підхід до роботи.

Відомо, що з давніх-давен  геометричні положення були основою для розвитку архітектури і будівництва. Володіння основами геометрії дозволяє майбутньому будівельнику успішно та раціонально розв’язати практичні проблеми. Геометричні задачі з будівельною тематикою допоможуть викладачам у формуванні  в учнів науково обґрунтованих професійних навичок.

Перпендикулярність у просторі. Застосування теореми про три перпендикуляри

Як буде проходити обрізний круг болгарки при розпилюванні лонжеронів рами?

Як за допомогою виска перевірити вертикальність бортів кузова вантажного автомобіля по відношенню до основи кузова?

Як розміщене свердло у свердлильному верстаті відносно станини?

Як розміщені кріпильні болти відносно площини кріплення?

Навести приклади, які зустрічаються у виробничій діяльності, щоб певні точки простору були рівновіддалені від усіх сторін многокутника. (Вісь болта, вал шестерні …)

Вантажний автомобіль ЗІЛ-130 тягне на буксирі легковий автомобіль ВАЗ-2106. У вантажному автомобілі форкоп знаходиться на висоті 1м від площини дороги, а у легковому автомобілі буксирна провушина розміщена від площини дороги на 0,5м. Якої довжини потрібно взяти гнучкий трос, якщо відстань між автомобілями 5м? (Врахувати захід троса під звіс автомобіля – 0,15м)

Зв'язок між паралельністю та перпендикулярністю прямих і площин

Про існування зв'язків між паралельністю і перпендикулярністю у просторі свідчить наш досвід. Справді , стовпи, встановлені вертикально, паралельні між собою; паралельними є вертикально спрямовані льодові бурульки, вертикальні колони, якими прикрашені споруди.

 

Добре відомий зміст аналогічних зв’язків у планіметрії: два перпендикуляри до однієї прямої є паралельними між собою, і навпаки, пряма, яка перпендикулярна до однієї з двох паралельних прямих, перпендикулярна і до другої. Однак стосовно прямих у просторі ці твердження не завжди виконуються. Натомість можемо вивчати випадки, пов’язані з паралельністю і перпендикулярністю прямих та площин.

Розглянемо детальніше зв'язок між паралельністю прямих і перпендикулярністю їх до площини. Ці зв’язки відображають відношення між реальними об’єктами , якими користуємося у повсякденному житті. Справді , якщо одну дошку паркану приладнано вертикально до поверхні землі, то другу дошку достатньо розмістити паралельно першій, щоб вона була вертикальною. Цей спосіб побудови паркану ґрунтується на теоремі про дві паралельні прямі, одна з яких перпендикулярна до площини.

 

Ця теорема є ознакою перпендикулярності прямої і площини, тобто за її допомогою встановлюють перпендикулярність прямої і площини. Її широко використовують не тільки в геометрії, а й у практичній діяльності. Спорудження будівлі з використанням виска є яскравою ілюстрацією застосування цієї ознаки перпендикулярності прямої і площини. Справді, нитка виска розміщена вертикально, і якщо ріг споруди паралельний нитці, то він також вертикальний.

Дана ознака природно породжує запитання: чи будуть паралельними дві прямі, які перпендикулярні до однієї площини? Відповідь на нього показує досвід (два вертикально встановлених стовпи – паралельні!) і він підтверджується теоремою, яка є оберненою до попередньої.

За допомогою теореми про паралельність прямих, перпендикулярних до площини, встановлюють паралельність прямих у просторових конструкціях. Адже вертикальність чи перпендикулярність до площини іноді легше перевірити (особливо на громіздких об’єктах ), ніж паралельність. Йдеться, наприклад, про розміщення поперечних балок при спорудженні стелі будівлі, розпізнавання паралельності прямих у геометричних конфігураціях.

Не менш важливими в геометрії та її застосуваннях є зв’язки між паралельністю площин та їхньою перпендикулярністю до прямої. Йдеться  про дві площини і одну пряму. Якщо дві площини паралельні і одна з них перпендикулярна до прямої, то як буде  розміщена друга площина по відношенню до цієї прямої? Як розміщені дві площини, якщо вони обидві перпендикулярні до прямої? Відповіді на ці питання також нам підказує досвід практичної діяльності. Якщо вбити цвях у дошку перпендикулярно до однієї сторони дошки, то він буде перпендикулярним і до протилежної. Якщо  на вісь колісної пари насадити колеса з обох боків так, щоб їхні площини були перпендикулярними до осі, то площини цих коліс будуть паралельними.

  

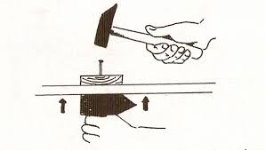
Ознака перпендикулярності прямої і площини пов’язана з розміщенням опорних колон відносно підлоги і стелі. Якщо площини підлоги і стелі паралельні, то колону досить поставити перпендикулярно до підлоги, щоб вона була перпендикулярною і до стелі.

Практичну цінність ознаки перпендикулярності ілюструє транспортування залізобетонної плити в горизонтальному положенні за допомогою крана.

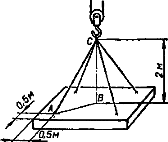
Для цього використовують 4 однакових троси, кінці яких закріплені на кутах плити і до гака. Оскільки плита висить вільно, то трос, на якому закріплено гак, перпендикулярний до поверхні землі і розміщений на прямій, що проходить через центр мас плити (для однорідної плити), який міститься на перетині діагоналей плити.

ЗАДАЧА. Чому льодові бурульки, які звисають з даху навесні, можна вважати паралельними між собою? Їх товщиною знехтувати.

ЗАДАЧА. На стелі закріплено гак. За допомогою канатів необхідно підвісити до нього платформу так, щоб її площина була горизонтальною. Як це зробити?

ЗАДАЧА. Два електричні дроти необхідно протягнути від стовпа висотою 7м до будівлі висотою 4м. скільки потрібно мати дроту, якщо відстань від будівлі до стовпа дорівнює 10м і на провисання дроту треба додати 3% від розрахункової довжини?

ЗАДАЧА. Сторожова вежа для охорони ділянки прямокутної форми встановлена в одній з вершин прямокутника. Відстані від спостерігача , що стоїть на вежі, до решти вершин прямокутника дорівнюють а, в , с, причому а>в>с. Чому дорівнює висота вежі ?

Перпендикулярність площин

Із усього розмаїття взаємних розміщень двох площин на особливу увагу і вивчення заслуговують ті, при яких площини перпендикулярні одна до одної (суміжні стіни кімнати, паркан і ділянка землі, двері і підлога)

Наведені приклади дають змогу побачити одну з основних властивостей відношення – симетричність розміщення кожної з площин відносно іншої. Симетрія забезпечується тим, що площини начебто «зіткані» із перпендикулярів.

Означення перпендикулярності площин можна проілюструвати , якщо розглянути фрагмент кімнати дачного будинку.

На ньому підлога і стіна складені із дощок, перпендикулярних до стіни і підлоги. Тому вони перпендикулярні. На практиці це означає, що підлога горизонтальна, а стіна вертикальна. Наведене означення важко використати при фактичній перевірці перпендикулярності площин.

У будівництві, побуті і техніці зустрічаємо перпендикулярні площини.

Якщо придивитися, то ми оточені перпендикулярними площинами. Стіни будинків зводять так, щоб вони були перпендикулярними до підлоги, а стеля, балкони – до стін, двері – до підлоги. Взаємно перпендикулярні суміжні грани цеглини, коробки сірників, пластівців, шафи, холодильника – взагалі кожного предмета, що має форму прямокутного паралелепіпеда. Диск пилки встановлюють так, щоб його площина була перпендикулярна до площини стола, площина каркасу – до поверхні землі. Рекламні щити розміщують на опорі, перпендикулярній до поверхні землі, тобто використовують ознаку перпендикулярності площин. Вбиті перпендикулярно до поверхні землі сваї тримають перендикулярно весь будинок.

ЗАДАЧА. Приладнати щит до стовпа так, щоб він був розміщений вертикально.

Якщо стовп стоїть вертикально, то досить довільно припасувати щит до стовпа і закріпити його. Якщо ж стовп стоїть похило до землі, то досить до стовпа приладнати вертикальну рейку, а потім щит припасувати і до рейки і до стовпа. У цьому випадку положення щита є цілком певним, оскільки стовп і вертикаль визначають єдину площину.

ЗАДАЧА. Секція паркану приладнана до вертикального стовпа. Чи можна стверджувати, що площина паркану вертикальна?

ЗАДАЧА. Як до рейки, паралельної до поверхні землі, прикріпити вертикальний щит?

ЗАДАЧА.. Чому поверхня дверей незалежно від того, зачинені вони чи відчинені, розміщена вертикально до підлоги?

ЗАДАЧА. Чому висок щільно прилягає до вертикальної стіни, а до похилої не обов’язково?

ЗАДАЧА. Чи можна до похилого стовпа прикріпити щит так, щоб він був перпендикулярним до поверхні землі?

ЗАДАЧА. Як на практиці встановити, чи перпендикулярна площина стіни до площини підлоги?

ЗАДАЧА. Пригадайте послідовність операцій при розмітці панелей на сходових клітках. Як обґрунтувати правильність розмітки панелей, застосовуючи теорему про перпендикулярність двох прямих площини? Зробіть відповідний малюнок, який підтвердить ваші висновки. Яка теорема планіметрії тут використовується?

Ортогональне проектування

Введення поняття перпендикулярності площин дає змогу повернутися до питань про зображення просторових геометричних фігур. Якість зображень у стереометрії, тобто можливість за ними отримати найбільш повне уявлення про фігуру, залежить від вибору напряму паралельного проектування. Серед усіх можливих напрямів проектування виділяється напрям, перпендикулярний до площини проекцій. По-перше, такий напрям лише один. По – друге, він найприродніший для сприйняття людиною.

           

Таким чином, одним із важливіших у геометрії та її застосуваннях окремими випадком паралельного проектування є ортогональне проектування, тобто проектування вздовж прямої, перпендикулярної до площини проекцій.

Ортогональне проектування , зазвичай, використовують і при зображенні кулі. В результаті зображенням кулі є круг. Якщо ж проектуючи прямі не перпендикулярні до площини проекцій, то проекцією кулі є частина площини, обмежена еліпсом (уявіть собі тінь, яка прямує аж до горизонту, від кулі, що лежить на землі), що не відповідає нашому уявленню про кулю.

Поняття перпендикулярності прямої і площини породжує один із найважливіших видів симетрії у просторі – симетрію відносно площини.

Прикладами симетричних відносно площини фігур насичені як реальний простір , так і геометричний. Природа створила симетричними фігури людей і більшість живих істот, симетричною є книга, яку тримаємо у руках, столовий посуд, праска, і багато іншого.

Вимірювання відстаней у просторі

Вимірювання відстаней між різними фізичними об’єктами є одним із найпоширеніших видів математичної діяльності людини. Якщо розмірами об’єктів можна знехтувати, то йдеться про вимірювання відстаней між точками, тобто про визначення довжин відрізків. В інших випадках моделювання даних об’єктів за допомогою точок при вимірюванні відстаней між ними недоцільне чи безглузде, наприклад, коли йдеться про вимірювання відстані між електролампою і столом, якщо першу можна ототожнювати з точкою, то для моделювання стола більш придатна площина чи її частина. Аналогічна ситуація виникає при визначенні відстані між фасадами будівель, що при математичному моделюванні зводиться до визначення  відстані між паралельними площинами; при встановленні вертикальної рейки на певній відстані від стіни (визначення відстані між паралельними прямою і площиною)

ЗАДАЧА. Як потрібно закріплювати дріт на стовпах, щоб забезпечити його паралельність до поверхні землі?

ЗАДАЧА. Як виміряти висоту дерева, не піднімаючись до його верхівки?

ЗАДАЧА. Плиту прямокутної форми підняли краном так, що три її вершини віддалені від поверхні землі відповідно , на  2м, 3м, 4м. На якій відстані від землі перебуває четверта вершина?

ЗАДАЧА. Спостерігач, що знаходиться на березі озера на висоті  h над рівнем води, бачить хмарку під кутом α , а її зображення  - під кутом β до горизонту. Знайдіть висоту хмарки над поверхнею озера при α  = 53⁰27^/, β=55⁰42^/, h= 76,8м.

ЗАДАЧА. Скільки  метрів телефонного кабелю потрібно, щоб його можна було протягнути від вершини стовпа довжиною 6м до даху будинку, де кабель кріплять на висоті 11м над землею, якщо відстань між стовпом і будинком 12м?

Вимірювання кутів у просторі

Взаємне розміщення прямих, прямих і площин, а також площин характеризуються у стереометрії різними способами. Один із них базується на кількості спільних точок цих фігур. Він приводить до важливих відношень між прямими і площинами – відношень паралельності. Уточнення взаємного розміщення вказаних фігур здійснюється за допомогою відношень перпендикулярності. Вони відображають певну симетрію взаємного розміщення фігур. Розгляд відстаней між фігурами дає змогу характеризувати їхнє взаємне розміщення за допомогою чисел. Подальше уточнення взаємного розміщення прямих і площин здійснюється за допомогою вимірювання кутів між цими фігурами. Необхідність таких вимірювань викликана  потребами як геометрії, так і практики. Вимірювання кутів необхідні в геометрії, геодезії, мореплавстві, космонавтиці тощо. Їх застосовують у повсякденному житті.

Поняття кута між прямою і площиною використовується багатьма фахівцями.

Практичну необхідність у вимірюванні кута між прямою і площиною можна проілюструвати на прикладах. Такими вимірюваннями здавна користувалися мореплавці при визначенні положення корабля. Вони необхідні геодезистам , які проводять роботи на місцевості, будівельникам при встановленні конструкцій.

Під певними кутами до площини горизонту споруджуються ескалатори на станціях метро, шахтні схили, фунікулери.

Кут між похилою і горизонтальною площиною геодезисти та маркшейдери вимірюють екліметром.

У його циліндричному корпусі (1) з прикріпленою до нього трубкою для візування (2) при натиснутій кнопці вільно обертається і встановлюється градуйований диск (3). Якщо кнопку відпустити, диск закріплюється і на його шкалі можна прочитати градусну міру кута, який вимірюють.

Якщо потрібна більша точність, такі кути вимірюють теодолітами.

Розглянемо особливості взаємного розміщення двох площин, які перетинаються. Це завдання пов’язане з практичною діяльністю людини і стане в пригоді при необхідності оцінки нахилу  даху до поверхні землі, врахування профілю місцевості при будівництві дороги, при виготовленні різців з різними властивостями різання. Отже, потрібним є вміння характеризувати взаємне розміщення непаралельних площин за допомогою числа після вибору одиниці вимірювання.

Вивченню многогранників передує таке поняття, як двогранний кут, многогранний кут. Найпростішими матеріальними моделями двогранного кута є краї різальних інструментів: зубил, стамесок, різців для токарних верстатів, ножі м’ясорубок тощо. Вимірюють такі кути кутомірами.

Як і у випадку визначення кута між прямою і площиною, потрібно знайти плоский кут, який характеризує взаємне розміщення двох площин. Дивлячись на обкладинки напіврозкритої книги, неважко побачити, що мірою взаємного розміщення обкладинок (мірою розгорнутості книги) може бути величина кута, який утворений краями обкладинок. Якщо розглядати площини, в яких розміщені ці обкладинки, то цей кут дістають як результат перериту даних двох площин третьою площиною, перпендикулярною до лінії перетину перших двох площин.

         

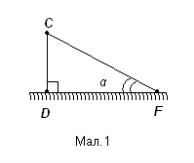     Види кутів у просторі (практичне застосування)

ШРБУ. При будівниці участків доріг, гребель, каналів, похилих дахів користуються кутом поперечного і поздовжнього схилу. Тобто на   мал. 1 - кут схилу і tg a = (1: 3 або 33°). Маємо приклад кута між площинами, причому для встановлення лінії горизонталі часто використовують нівелір. На виставці приладів можна розкрити принцип його дії.

Відомі також кути природного схилу сипучих матеріалів: бурта картоплі - 45°, вугілля - 42°, ґрунту - 40°, глини - 30°, піску – 25-35°. Їх ще називають кутами природного укосу (між твірною насипу і площиною землі).

Управління автошляхів. При проектуванні і будівництві автомобільних доріг враховують так званий кут перелому поздовжнього профілю дороги (див мал. 2 ). Він зумовлює видимість зустрічних авто і часто профіль змушено скруглюють, знімаючи верх стрімкого горба, щоб уникнути аварійно небезпечних ділянок траси. Маємо приклад використання кута між півплощинами.

Укрзалізниця. У точках спряження паралельних колій і на поворотах кут укосу створюють спеціально, щоб зрівноважити відцентрову силу (мал. 3). Для цього зовнішню рейку піднімають над внутрішньою – міліметр підйому   на кожний метр шляху (але не більше h = 125 мм сумарно, тобто кут укосу буде обраховуватись так: tg a_max = = 0,0822; a_{max ≈} 5°).

Селянська спілка. Відразу після збору урожаю стерню рихлять на невелику глибину, щоб спровокувати до росту насіння бур’янів. Такий обробіток називається лущенням. Диск лущильна представляє собою ввігнутий диск-тарілку (d = 450 мм), встановлений вертикально під деяким кутом а до напрямку руху, його називають «кут атаки» (мал. 4). При h = см, а = 31°.

Диск лущильника бур’янів встановлюють не вздовж напряму руху трактора, а під кутом 31° до цього напряму оптимально. Під більшим кутом не можна, бо диск швидко обірве опір ґрунту.

Напрям сили тяги причіпного плуга повинен становити із поверхнею землі 26° оптимально, щоб зусилля трактора не були надто великі і огріхи менші (мал. 5).

Тут спостерігаємо використання кута між похилою і площиною. Самі механізатори це не обраховують, а намагаються при ремонті зберегти вигляд, створений інженерами.

 Будівництво.При зварюванні татові зовсім не байдуже, під яким кутом тримати електрод, а під яким – газовий пальник до поверхні металу. Електрод обов’язково тримати під кутом 45° до поверхні зварювання, бо в разі збільшення кута шлаки і шкідливі домішки будуть потрапляти в зону зварювання, що дасть неякісний шов зварювання (демонструється розміщення електрода). При меншому куті буде поганий провар металу і спостерігатиметься його розбризкування. Отже, 45° - оптимальний кут між похилим електродом і площиною зварювання.

Аеропорт. Кути між мимобіжними прямими враховують при прокладанні повітряних трас для літаків; кут між прямою і площиною – при зльоті і посадці літаків. Літак-пожежник приземляється на воду тільки під строго визначеним кутом (величину не повідомлялось), оскільки при його перевищенні буде сильний удар об воду і можливий вибух.

     Шкільна майстерня. Заочна екскурсія у шкільну майстерню, де ми зустрічаємо повсюдне врахування кутів різних видів. Наприклад, лезо рубанка заточують під кутом 30°-35⁰, а встановлюють під кутом 45°-50° до площини підошви (демонструє це), слюсарні зубила заточують для чавуну, сталі під кутом 70°; міді, латуні - 45°; алюмінієвих сплавів - 35°.

Свої норми кутів заточування існують для різців, стамесок, сокир. Для перевірки вказаних кутів існують шаблони і кутоміри (їх можна подивитись на виставці чи більш детально розповісти принципи дії).

Подача деталі в токарному станку найчастіше здійснюється під кутом до горизонтальної площини.

  Геодезія і картографія. У геодезії і картографії, маркшейдерській справі (підземні прохідники) – від простих вимірювань до найскладніших – усім править знання про кути. На виставці ми маємо екліметр – пристрій для вимірювання величини кута нахилу прямої до горизонту (мал. 6). OP – нитка з вантажем, яка показує на шкалі величину шуканого кута POB. Доведіть: POB = PSO  (SOP + POB = 90° і PSO +SOP = 90°). Знання про кути і декартові координати допомагає встановити напрям прокладання тунелю в скелі, напрям підземних комунікацій (напрям лінії метро) у місті. Адже треба врахувати всі вже існуючі кабелі, труби, допустимі відстані до них.

Знаючи початкові і кінцеві координати нового об’єкта вираховують кут його прокладання.

ЗАДАЧА. Антену закріплюють за допомогою чотирьох розтяжок однакової довжини, виготовлених із троса. Відомо, що для надійного кріплення антени розтяжки повинні бути натягнуті під кутом, не більшим від 600 до поверхні землі. Чи вистачить для кріплення 80м троса, якщо точка кріплення міститься на висоті 15м над поверхнею землі і на закріплення однієї розтяжки йде до 1м троса?

Зазначимо, що у практичних задачах поширенішою є не конструкція з двох  площин , які перетинаються, а конструкція двох півплощин , що мають спільну межу (схили даху, обкладинки книги, стінки жолоба тощо).

ЗАДАЧА. Довжина ручки швабри дорівнює 1,2м.

1.     На якій відстані від підлоги розміщений кінець швабри при витиранні підлоги, якщо швабра нахилена до неї під кутом 60⁰?
2.     Який кут утворить ручка швабри з підлогою, якщо кінець ручки віддалений від підлоги на 0,6м?

ЗАДАЧА.. Канатна дорога протягом 15хв піднімає лижника на вершину гори від її підніжжя зі швидкістю 2м/с. Визначте висоту гори, вважаючи, що кут нахилу гори приблизно дорівнює 30⁰.

ЗАДАЧА. Послуговуючись законами відбивання світла, доведіть, що падаючий промінь і відбитий утворюють із дзеркалом однакові кути.

ЗАДАЧА. Дах будинку має форму чотирикутної піраміди, в основі якої лежить квадрат зі стороною 10м. Відомо, що площини даху утворюють з площинами фундаменту кути 45⁰, а крокви розміщені одна від одної на відстані 1м (по осях).

Знайти :

-  довжину усіх крокв,

• висоту даху,
• довжину ребра даху.

ЗАДАЧА. Дах будинку має форму чотирикутної піраміди, в основі якої лежить прямокутник зі сторонами 8м і 12м. Які кути утворюватимуть площини даху з площиною фундаменту , якщо висота даху 5м?

ЗАДАЧА. При шпаклюванні шпатель тримають під різними кутами до поверхні, яка вирівнюється. Покажіть за допомогою шпателя кути, які утворюються. Якої величини вони допускаються, як залежить величина кута від товщини шару шпаклівки? Як називаються такі кути в геометрії?

ЗАДАЧА. Крізь гору між точками А і В треба покласти горизонтальний тунель. З точки С, яка розміщена на висоті над тунелем, відрізок АВ видно під кутом γ , а з точок А і В точку С видно під кутами α і β  над горизонтальною площиною. Знайдіть довжину тунелю.

ЗАДАЧА. Кут падіння вугільного пласта дорівнює 35⁰. При вертикальному бурінні виявлено, що довжина шляху бура у вугіллі дорівнює 2,2м. Обчисліть товщину пласта.

ЗАДАЧА. Обчисліть товщину m кам’яновугільного шару , площина якого нахилена під кутом α=14⁰40^/ до площини горизонту, якщо при вертикальному бурінні встановлено, що глибина шару в=4,4м.

ЗАДАЧА. Знайдіть товщину т вугільного пласта, якщо вертикальна свердловина нахилена до нього під кутом φ =72⁰ і проходить по вугіллю відстань h=2,5м.

 

ЗАДАЧА. Із заготовки товщиною 20мм треба виготовити стамеску з кутом загострення 12⁰. На якій відстані від краю заготовки повинна починатися загострена частина?

ЗАДАЧА.В яких випадках на виробничій практиці доводиться мати справу з кутами між двома площинами, які перетинаються? Наведіть приклади вимірювання таких кутів при виконанні виробничих операцій.

Так при вивченні многогранних кутів корисно розв’язати декілька задач на знаходження елементів покрівель будинків.

ЗАДАЧА. Завіси даху утворюють прямокутник ABCD. AB=12м; BC=30м; кут нахилу скатів – 30⁰. Довести , що нахили скатів рівні. Знайти площу поверхні покрівлі.

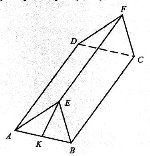
Розв’язання

1.Скати даху представляють собою рівні прямокутники BCFE і ADFE.

          2. Прямокутник ABCD розташований горизонтально.

          3. Площина трикутника ABE і CDF перпендикулярні до площини ABCD.

          4. Так як скати даху – прямокутники, то EF паралельна AD. Отже, за ознакою паралельності прямої і площини EF паралельна площині ABCD.

          5. Скат BCFE утворює двогранний кут, ребро якого – ВС. Побудуємо лінійний кут двогранного кута. Проведемо EK перпендикулярно АВ, оскільки ∆ АВЕ перпендикулярний ABCD, то ЕК перпендикулярно ABCD. Похила ВЕ перпендикулярна ВС, отже, її проекція ВК перпендикулярна ВС. Отже, кут АВЕ=β – лінійний кут двогранного кута, який утворений скатом BCFE і площиною ABCD.

Аналогічно можна довести, що кут ЕАВ – лінійний кут двогранного кута, який утворений скатом AEDF і площиною ABCD.

6. Розглянемо трикутник АВЕ, він рівнобедрений, отже, кут ЕАВ дорівнює куту ВАЕ, тому вони - рівні і є двогранними кутами. Отже, скати даху нахилені до горизонталі однаково.

7. S_покр. =2^.ВЕ^.ВС; 

S_покр. =2^.30^.6,93 = 415,81 (м²).

Відповідь. S_покр. = 415,81 (м²).

Координати і вектори у просторі

Поняття «вектор» увів у 1846р. ірландський математик В.Гамільтон. Спочатку  вектори використовували переважно у фізиці для зображення сили, швидкості та інших векторних величин, тому вектори  ототожнювали із напрямленими відрізками. У сучасній математиці поняття вектора набагато змістовніше.

За допомогою координат і векторів можна розв’язувати багато цікавих і важливих задач з фізики, астономії, геодезії та інших прикладних наук. Частина математики, в якій розглядають методи розв’язування геометричних задач за допомогою координат і векторів, називається аналітичною геометрією. Вектор – це елемент векторного простору.

 Більш як за 100 років до н.е. грецький астроном Гіппарх з Нікеї запропонував покрити на карті землю кулю паралелями і меридіанами і ввести  добре відомі тепер географічні координати. В ХІУ ст. французький математик  М. Орезм ввів , з аналогією з географічними, координати на площині, якими пов’язав геометрію із алгеброю. Під час використання цього методу точка площини (геометричний об’єкт ) замінюється парою чисел (х;у), тобто алгебраїчним об’єктом. Та головна заслуга в створені  методу координат належить французькому філософу, математику, фізику Рене Декарту (1596-1650). Декарт ввів систему прямокутних координат, якою користуємося ми, в широке застосування і поклав початок розвиткові важливої математичної науки – аналітичної геометрії. Основна думка Декарта полягала у тому, щоб примусити алгебру працювати на геометрію і навпаки. Алгебра має справу з числами та рівняннями. Геометрія – з точками, лініями, поверхнями Як він поєднав ці дві науки? У системі координат встановлює відповідність між точкою і впорядкованою парою чисел – її координатами, потім – між кривою та її рівняннями. Таким чином було встановлено відповідність між кривою (поверхнею) та її рівнянням,  з’явилась можливість описувати величини графічно. А якщо задача сформульована на мові координат, то її розв’язування  може бути проведено чисто алгебраїчними методами, без складних креслень.

Що ж це дало математиці?  З’явилась можливість за рівнянням з двома змінними будувати графік та описувати величини графічно. Коли ми бачимо температурну криву чи кардіограму, як штурман прокладає на карті маршрут корабля – це застосування нової геометрії. Навпаки, є можливість записувати рівняння ліній та легко відповідати на запитання, чи вони перетинаються (якщо це навіть траєкторії космічних тіл), оскільки досить розв’язати відповідну систему рівнянь. Так можна передбачити сонячні та місячні затемнення, «парад планет», можливість зіткнення комети із Землею. Метод координат подарував людству планету «на кінчику пера». Незалежно один від одного французький астроном Левер’є та англійський вчений Адамс під час дослідження відхилення від розрахункової орбіти у русі планети Уран, висунули припущення про існування невідомої досі планети Сонячної системи і розрахували її координати. Напрямлені телескопи у задані точки відправили в планету Сонячної системи – Нептун. А у 1915 році було математично доведено існування дев’ятої планети – Плутон, яку побачили у телескоп лише у 1930 році.

Наприклад, щоб встановити, чи досягне комета Землі, космічний апарат планети, коли було (буде) сонячне затемнення досить скласти і розв’язати  відповідну систему рівнянь. Але головне – стало можливим завдяки розвитку обчислювальної техніки застосування координат (і векторів) в техніці: суть у тому, що ЕОМ вміють оперувати тільки з числами або інформацією, записаною з допомогою чисел. І коли ЕОМ управляє літаком, підводним човном, космічним кораблем, вона обробляє дані про положення , швидкість , прискорення тіла (тобто з геометричної точки зору, дані про точки і вектори) не в геометричній формі, а в перекладі на мову чисел, за допомогою координат.

Положення літака в повітрі неможливо описати за допомогою тільки двох координат, тобто за допомогою координат проекції літака на поверхню землі (довготи та широти), необхідно знати ще й висоту літака над поверхнею землі.

Системи координат часто використовуються в прикладних науках і на виробництві. У трьох взаємно перпендикулярних напрямах (за осями координат) переміщуються робочі вузли багатьох сучасних верстатів.

Графічне зображення діяльності серця – кардіограма є, по суті , вектор – функцією, що містить 12-18 компонентів, кожний з яких є числовою функцією часу. Тому лікар, який вивчає кардіограму пацієнта, працює в 12 або 18-вимірному просторі. І тут йому не обійтись без комп’ютерної програми, яка будує математичну модель роботи серця на основі теорії п- вимірних просторів. Наприклад, перевіривши кардіограму хворого, програма визначає оптимальні фізичні навантаження лікувальної фізкультури, кращий час прийому процедур, виявляє найменше відхилення від нормальної роботи серця і тим розширює можливості профілактичного лікування.

Існують координатно-розточувальні та інші верстати із числовим програмним керуваням.

Безконсольний вертикально-фрезерний верстат з хрестовим столом і числовим програмним керуванням

Фрезерний верстат з ЧПУ

Малогабаритний верстат для лазерного різання металу

Установка 2D/3D лазерного різання Domino

У прикладних науках і техніці використовуються циліндрична, сферична та інші системи координат. Приклад сферичної системи координат – сітка паралелей і меридіанів на глобусі. Конструктори і наладчики різних роботів і роторних механізмів використовують циліндричну  систему координат. Відомо , що комп’ютери видають різні траєкторії, графіки, схеми та інші геометричні образи. Здійснюється це завдяки обчисленням координат їхніх точок.

У геометрії розглядаються тільки вільні вектори. Фізики частіше використовують прикладені (зв’язані) вектори, які визначаються не лише довжиною і напрямом, а й точкою прикладання. У картографії векторами називають будь-які відрізки, навіть криволінійні, які показують напрями морських течій, руху армії тощо. Такі «вектори» не можна ні додавати , ні множити.

Спочатку вектори використовували переважно у фізиці для зображення сили, швидкості та інших векторних величин, тому вектори ототожнювали з напрямленими відрізками. У сучасній математиці поняття  вектор набагато змістовніше. Вектор – це елемент векторного простору. А векторним простором називається будь-яка множина, для елементів якої визначені операції додавання і множення на число.

У двовимірному просторі (на площині) точка чи вектор задається двома координатами, у тривимірному – трьома. За аналогією можна розглядати простір, точки та вектори якого визначаються чотирма координатами. Такий простір називають чотиривимірним.

Геометрію чотирьох вимірів одним з перших  опрацював український учений Микола Іванович Гулак.(1822-1899)

У 1877 році опублікував монографію «Спроба геометрії чотирьох вимірів». Р.Іваничук написав про нього роман «Четвертий вимір».

Геометричні перетворення у просторі і їх властивості пояснюють координати і вектори у просторі.

Симетрія – одне із геометричних перетворень.

Властивості симетрії застосовуються у творах декоративного і прикладного мистецтва. Дуже часто різні архітектурні прикраси, орнаменти симетричні відносно певної осі. Симетрично оформляють фасади будинків, вікна, двері. Симетричні візерунки роблять на тканинах, шпалерах.

Чудові орнаменти пам’яток стародавньої архітектури (Вавілон, Єгипет) свідчать про те, що й тоді було надзвичайно розвинуте відчуття симетрії. Стародавні будови вражають гармонійністю своїх форм.

З симетрією ми зустрічаємося всюди-у природі, техніці, мистецтві, науці.

Поняття симетрії проходить крізь всю багатовікову історію людської творчості. Воно означає врівноваженість, упорядкованість, красу, довершеність, доцільність.

«Для людського розуму симетрія має, мабуть, цілком особливу приваблюючу силу. Нам подобається дивитися на прояв симетрії у природі, на ідеально симетричні сфери планет чи Сонця, на симетричні кристали, на сніжинки, нарешті, на квіти, які майже симетричні», - писав американський фізик Річард Фейнман.

Із симетрією зустрічаємося у природі – листя дерев, квіти, метелики, морські зірки.

У природних формах бачимо два типи симетрії: дзеркальну, або «симетрію листка» (листок, метелик, лялечка), та радіально-променеву або «симетрію ромашки» (гриби, ромашка, соняшник, морські зірки, сніжинки).

Загальний закн симетрії виявляється у природі: усе, що росте і рухається по вертикалі, тобто вгору, або вниз відносно земної поверхні, має симетрію у вигляді пучка площин симетрії, які перетинаються («симетрія ромашки»); все, що росте і рухається горизонтально чи похило відносно земної поверхні, має дзеркальну симетрію («симетрія листка»).

Якщо вздовж тіла гідри провести уявну вісь, то її щупальця розходитимуться від цієї осі в усі боки, як промені від джерела світла. Таке розміщення частин тіла називають променевою симетрією. Звисаючи з якої-небудь водяної рослини, гідра постійно похитується з боку в бік і повільно водить щупальцями, пістерігаючи здобич. Жертва може з’явитися з будь-якого боку, тому променево розставлені щупальці найкраще відповідають такому способу полювання.    

Симетричні відносно площини молотки, рубанки, стамески, лопати, викрутки, цеглини, труби, підшипники, автомобілі, літаки, ракети, кораблі і багато інших знарядь праці і механізмів. А також деякі овочі, комахи, архітектурні будівлі.

Симетрія також використовується у дизайні одягу.

В українських вишиванках бачимо геометричний орнамент з багатоколірною гамою, чітко вираженою симетрією відносно певної точки чи лінії, вміле поєнання геометричних фігур «у квітку».

Чітко помітна симетрія при розгляді витинанок. Осі симетрії мають і друковані літери українського алфавіту.

Вчення про симетрію многогранників важливе для кристалографії. Виявляється, один і той самий кристал у різних напрямках має різні фізичні властивості, наприклад, твердість. І виявляти ці напрями допомагають дослідження  симетрії кристалів.

Симетрію відносно площини називають ще відображенням у площині. Наприклад, відображення фігури у дзеркалі чи на поверхні спокійної водойми: озера, річки.

З геометричними рухами тісно пов’язане поняття рівності фігур. З рівними матеріальними предметами доводиться мати справу багатьом робітникам. Сучасна промисловість виробляє великі партії геометрично рівних виробів. Рівні всі заготовки, вилиті  в одній формі, всі деталі, виготовлені верстатом-автоматом за однією програмою. На багато виробів існують спеціальні державні стандарти. Служба стандартизації зобовязує випускати такі вироби встановлених стандартів, геометрично рівні один одному.

 

      

Геометричні тіла і поверхні

Фізичний світ вражає нас різноманіттям форм, адже кожний реальний об’єкт має свої особливості, які відрізняють його від інших. І в той же час предмети, що оточують нас, мають багато спільних рис, які при описанні їх засобами геометрії дали змогу природно виділити серед них обмежену кількість основних класів геометричних фігур. Цегла, керамічна плитка, дерев’яний брус та й самі будівлі найчастіше мають форму прямокутного паралелепіпеда. Сонце, планети, яблуко, деякі овочі, краплю води ми описали б за допомогою геометричної фігури – кулі. Характеризуючи форму стовбурів дерев, чашки для кави, олівця, згадуємо про прямий круговий циліндр (можливо і конус).

Що в першу чергу бачить спостерігач, дивлячись на предмет? Звичайно його «зовнішність». А потрібно вивчити будову поверхонь геометричних тіл. Заглянути всередину тіл допоможуть перерізи. Вони дають змогу краще виявляти форму предметів.

За допомогою поперечного перерізу дерева можна встановити його вік. Використовуючи переріз Землі, отриманий за допомогою супутників, людство мало зиогу дослідити її будову. У будівництві перерізи застосовують для обчислення міцності балок, колон, опор.

А ще цікавішими є властивості симетрії.

З різними, іноді дуже складними, матеріальними моделями многогранників мають справу представники різних професій.

Столяр має справу з многогранниками, вистругуючи бруски, видовбуючи в них  прямокутні отвори або заглибини. Муляр кладе стіни, споруджуючи будівлі, у формі многогранників. І каменярі, теслі, шліфувальники, стругальники, гранувальники, мінералоги, кристалографи та інші спеціалісти – всі мають справу з многогранниками.

Вивченню многогранників передує таке поняття, як двогранний кут, многогранний кут. Найпростішими матеріальними моделями двогранного кута є краї різальних інструментів: зубил, стамесок, різців для токарних верстатів, ножі м’ясорубок тощо. Вимірюють такі кути кутомірами.

Призма

Існують  певні уявлення про опуклі та не опуклі многогранники, про їх грані, ребра, вершини, поверхню. А якої форми тіла найбільш поширені у навколишньому середовищі?(кришка стола, сірникова коробка, балки, форма будинків та кімнат, цеглина). Як відомо у стереометрії нас цікавить форма тіл та їх розміри. У названих предметів схожа форма. (основи –паралельні та рівні, бічні грані-прямокутники або квадрати) Поверхня всіх тіл складається зі скінченої кількості многокутників, причому, дві грані-рівні п-кутники, а решта п граней – паралелограми. Такі тіла називаються призмами. 

Вивчення далеких періодів людської культури, сліди якої навчилася розпізнавати археологія, підводить до переконання , що спочатку споруди були неправильної форми: в них позначилася звичка людини до використання природних укриттів – печер. Чому ж багато будинків сьогодні – це споруди, які мають форму прямокутних паралелепіпедів? Прямокутна система побудови архітектурної форми була обумовлена статичною основою споруд, будівельними матеріалами, головним чином деревом. Людина створила собі світ прямокутних речей, видобуваючи із природи те, що може послугувати її потребам, - це результат діяльності людського розуму.

Велика Китайська стіна – фортечна стіна у Північному Китаї, була споруджена в 4-3 ст. до н.е. для захисту від нападу кочових племен. Її довжина 5тис.км, висота – (в середньому) 8м, а ширина -5м.

Існує багато інструментів призматичної форми. Масштабна лінійка-основна її частина являє собою чотирикутну призму трапецеподібного перерізу. Напилок – слюсарний інструмент, який служить для обпилювання металічних виробів. Він являє собою чотирикутну призму із ромбовидним перерізом. Гайка має форму правильної шестикутної призми. Гайки використовуються у з’єднанні  із болтом, як кріпильна деталь для з’єднання двох (або більше) деталей машин або предметів. Болт є круглим стержнем, на одному кінці якого є головка у вигляді правильної шестикутної призми. В частинах, які скріпляються , висвердлюється круглий отвір, де вставляється болт, що загвинчується гайкою.

У спорті теж не обходяться без знарядь у формі призми. Спортсмени стрибають у висоту через дерев’яну планку  трикутного перерізу 3х3 см або через дюралеву трубку діаметром 23-26мм , в обидва кінці якої вставляють дерев’яні буші трикутного або квадратного перерізу.

У фехтуванні використовуються три види холодної зброї. Рапіра –колюча зброя; має легкий еластичний клинок прямокутного перерізу довжиною 90см. Маса рапіри-500г. Шпага –колюча зброя  із жорстким тригранним клинком довжиною 90см. Маса шпаги -770г. Шабля – зброя; має клинок довжиною 105см фігурного перерізу, з подовжніми пазами на бічній частині.

Для гри в настільний теніс виготовляють стіл висотою 0,76м від підлоги. Для кришки беруть фанеру або дошки товщиною 30мм. Розмір кришки –2,74м х 1,525м. М’яч використовують із целулоїду або пластика масою 2,5г.

Для природи , яка оточує людину, прямокутна форма жодною мірою не є характерна, правильна форма окремих кристалічних утворень ніяк не спростовує цього твердження. Кристали різних речовин відрізняються один від одного формами. Кубики кристалів кам’яної солі не сплутаєш зі стовпчиками берилу або табличками мідного купоросу; форму шестигранних призм має кварц.

В природі дуже мало об’єктів призматичної форми. Цікавою  є інформація про місцевість в Африці, яка називається Низький Велд. Характерна для цього ландшафту –численні невеликі пагорби , які тут відомі як «копі». Це груди, практично кубічних валунів, ніби поскладених один на одного рукою людини. За схожістю зі старовинними баштами їх називають «замками » копі. Характерна прямокутна форма валунів пояснюється тим, що з’єднувальний матеріал вивітрюється швидше, ніж тверда серцевина кожного блоку.

Рослин призматичної форми не існує. Проте – у басейні Нілу (краї неосяжних боліт) росте папірус, з якого в давнину в Єгипті виготовляли папір. Папірус має тригранні стебла висотою до 4,5м.

І звичайно , стільники у вуликах мають шестигранну форму. Будовою стільників дуже давно цікавилися не лише математики. Займалися нею філософ-фізик Аристотель  (ІУ ст. до н.е.), природознавець Пліній Старший (І ст. н.е.), фізик Реомюр (ХУІІІ ст.), математики: Папп(ІІІ ст.), Ян Брожек (ХУІІ ст.), Кеніг, Маклорен, Люйллер (ХУІІІ ст.), Лаланд, Браутгхам (ХІХст.) . Бджоли своєму житлу надавали таку форму, щоб за мінімальних витрат матеріалу (воску) та витрат часу побудувати найбільш просторе приміщення і максимально раціонально використати невеликий простір вулика. Вже Піфагор помітив, що існує лише три види правильних многогранників, за допомогою яких можна без порожніх місць покрити всю площину навколо будь-якої точки: рівносторонній трикутник, квадрат і правильний шестикутник. Лише одна із цих фігур може бути основою комірки (із мінімальним периметром і максимальною площею поверхні). Таку властивість має правильний шестикутник. 

Після опрацювання відповідного стереометричного матеріалу , потрібно застосувати отримані знання для розв’язування прикладних задач. Саме потреби практики, життя привели до створення та вивчення поняття призми.

Протягом усього життя ми маємо справу із предметами, частини яких або вони самі мають форму паралелепіпеда.

Форму прямокутного паралелепіпеда мають цеглини, бруски, контейнери, ящики для овочів і фруктів, деякі упаковки продуктів харчуваня, ліків. З непрямокутними паралелепіпедами часто доводиться мати справу мінералогам і кристалографам.

 

    

Правильні призми досить часто використовуються в техніці, будівництві, оскільки різноманітні деталі, конструкції мають форму призми. Зокрема, заготовки для гайок  мають форму правильної шестикутної призми, іноді трикутної, чотирикутної чи восьмикутної. Нерідко форму призми мають башти, частини споруд.

ЗАДАЧА. Чи можна визначити відстань між протилежними верхнім та нижнім кутками кімнати, користуючись звичайною лінійкою?

ЗАДАЧА. По стінках кубічного приміщення з нижнього кута в протилежний верхній кут необхідно прокласти електродріт. Яким має бути маршрут прокладання, щоб довжина дроту була найменшою? Скільки таких маршрутів?

Паралелепіпед

ЗАДАЧА. У кімнаті, що має форму прямокутного паралелепіпеда, є два вікна та одні двері. Скільки рулонів шпалер (без малюнка)потрібно придбати, щоб обклеїти стіни цієї кімнати, якщо відомі розміри (у м) кімнати -4х5х2,8; вікон -1,2х1,84 дверей – 0,9х2,1; рулону – 0,5х10. Врахуйте, що відходи становлять 5%.

ЗАДАЧА. Розміри цеглини – 250х120х65мм. Знайдіть відстань між її найвіддаленішими точками.

Піраміда

Частини багатьох споруд мають пірамідальну форму. Безумовно , до них належать славетні єгипетські піраміди.

ЗАДАЧА. Відома піраміда Хеопса в Єгипті має форму правильної чотирикутної піраміди. Її висота – 147м, а площа основи – 5,3га. Знайдіть кут нахилу її бічного ребра до площини основи.

Многогранники є одним із важливих видів просторових геометричних фігур. Поверхні  многогранників складаються з многокутників, подібно до того, як межі многокутників – з відрізків. Саме ця властивість многогранників визначає їхню роль у моделюванні просторових форм об’єктів навколишнього середовища, зокрема тих, які людина широко використовує у своєму житті.

Правильні многогранники

Форму куба мають кристали кухонної солі та деякі алмази. Інші алмази кристалізуються у формі  правильних октаедрів. Кристали піриту (залізного колчедану) мають форму правильного додекаедра. Властивості правильних (і похідних від них) многогранників використовують також архітектори і будівельники, які створюють просторові конструкції.

ЗАДАЧА. Аденовірус має форму одного з правильних многогранників – ікосаедра. Цим досягається максимальна економія генетичної інформації. А згідно із законами математики, щоб у найбільш економний спосіб побудувати замкнену оболонку з однакових елементів, потрібно скласти з них саме ікосаедр, який і виявлено у конструкції вірусу.

Всі так звані сферичні віруси, у тому числі й вірус поліомієліту , - це маленькі ікосаедри, а не сфери, як вважали донедавна. Правильні многогранники, у певному розумінні, - найзручніші фігури, і природа не оминула цієї їхньої властивості в конструюванні просторових форм матерії, починаючи з молекулярного рівня. Обчислити об’єм і площу поверхні ікосаедра, якщо його ребро дорівнює а.

ЗАДАЧА. Один із алмазів, добутих у Якутії, важить 42 карати і має форму правильного октаедра. Знайдіть ребро цього октаедра. (Густина алмазу 3,5 г/см³, 1 карат =0,2г)

Тіла обертання

Більшість  деталей, які виточують на токарних станках із металу і дерева – тіла обертання. І посуд, виготовлений на гончарних кругах, і скляні банки, пляшки, графини, стакани, пробірки, і різноманітні котушки , барабани, вали, шайби, заклепки, лінзи, патрони, знаряддя, спортивні диски, м’ячі, обручі – це все матеріальні тіла, що мають форму тіл обертання.

Одним із важливих способів побудови тіл у природі і в результаті діяльності людей є утворення їх за допомогою обертання плоскої фігури навколо осі, яка належить площині, де міститься фігура (циліндри, конуси, кулі). Важливість цього класу тіл пов’язана з тим, що людина здавна виробляла предмети, які мають форму тіл обертання. Це і виготовлення глиняного посуду за допомогою гончарного круга, і обробка металу чи деревини на токарних верстатах.

Фігури обертання широко використовуються для описання геометричних форм у навколишньому світі, у практичній діяльності. Це пов’язано як зі способом їх утворення, так і з їхніми властивостями симетрії.

ЗАДАЧА. Обертанням якої фігури і навколо якої осі можна дістати фігуру, форму якої мають:

-         круглий загострений олівець, глиняна миска, склянка, дзеркальна поверхня прожектора?

Циліндр

Тіла циліндричної форми дуже поширені. Стовбури дерев мають приблизно циліндричну форму. Їх використовують для будівництва житл, мостів та інших споруд. Ця форма поширена і в архітектурі. Наприклад, колони циліндричної форми прикрашали величні споруди стародавньої Греції. Циліндричну форму мають резервуари для нафти, циліндричні труби, катки для укачування асфальту, цистерни для молока, корпуси водонапірних башт, ринви, рулони паперу, шпалери, валики для побілки і окраски і т.д.

Циліндричну форму має основна частина космічної ракети, яка містить двигуни і пальне.

У Франції навіть споруджено багатоповерховий будинок циліндричної форми. До речі, дають про нього позитивні відгуки.

У швейній промисловості багато предметів і деталей швейних машин мають циліндричну форму:

- вали (головний, розподільний, човниковий, вал переміщення );

- голкотримач;

- шестерні;

- складова частина регулятора натягу верхньої нитки;

- центрові пальці;

- барабани механізму човника і т.д.

Котушки швейних ниток мають циліндричну форму. Футляр для сантиметрової стрічки – порожнистий циліндр.

А скільки побутових предметів, з якими ми зустрічаємося у повсякденному житті, мають форму циліндра.

Засоби побутової хімії містяться у циліндричних упаковках. Флакони і тюбики для косметичних засобів часто виготовляють циліндричної форми.

Якщо розглянути власну кухню, то предметів даної форми там безліч.

Дослідженнями циліндричних поверхонь і їх властивостей займалися досить давно.

Спосіб обчислення бічної поверхні циліндра знайшов ще Архімед.

Те, що всі точки кола однаково віддалені від центра, безпосередньо застосовується на практиці. Наприклад, в автомашині, завдяки коловій формі ободку колеса, вісь, на якій воно обертається при русі автомашини, весь час залишається на одному рівні від поверхні, по якій переміщується автомашина. Внаслідок цього забезпечується горизонтальне переміщення пасажирів або вантажу.

Цікаво, що людина з зав’язаними очима не може іти по прямій лінії. Вона обов’язково зійде з прямого шляху на коловий. Є багато прикладів, коли люди, які заблудилися, поверталися у вихідне місце.

Те саме спостерігається і у тварин. Собака з зав’язаними очима плаває по колу. Зацькований звір, що втратить від страху свідомість, рятуючись від переслідування, біжить по колу. У цьому не має нічого дивного. Адже, щоб зберегти прямолінійний напрям, не контролюючи його очима, тіло повинно бути точно симетричним, а це в живій природі абсолютно не можливо. Отже, рух по колу відбувається в описаних випадках через асиметричну розвиненість правої і лівої руки, сторін тіла людини і тварини. А коли людина або тварина рухається з відкритими очима, то останні корегують їх рух.

Циліндрична форма предметів, конструкцій, будівель зустрічається на кожному кроці.

 

    

    

Циліндричні резервуари і цистерни, хокейні шайби, графітні стержні, електроди для електрозварювання, круглі олівці – всі вони мають форму прямого кругового циліндра. І шахтний стовбур, бурова неглибока свердловина, отвір , просвердлений у дошці перпендикулярно до її поверхні, циліндр двигуна внутрішньо згоряння або поршневого насосу – також циліндри.

Ще більше зустрічається матеріальних циліндрів у комбінації з іншими тілами: призмами, кулями пірамідами, циліндрами. Наприклад, цегла з отворами, залізобетонна панель для перекриття, труба, просвердлена по осі куля.

Кругові циліндри і призми в технічних і будівельних конструкціях часто-густо пов’язані між собою. У технічних застосуваннях «вирізування » з даної фігури вписаної є найекономнішим з точки зору використання матеріалу.

ЗАДАЧА. Із циліндричної колоди, що має довжину l і діаметр основи d, вирізати найміцніший брус прямокутного перерізу. (Цілком природним є припущення, що міцність бруса даної форми суттєво пов’язана з площею поперечного перерізу: чим більша площа, тим міцніший брус). Математичною моделлю задачі є побудова вписаної в прямий круговий циліндр (модель колоди) призми з прямокутною основою (модель бруса) найбільшої площі. Довжина колоди (висота циліндра) ролі не відіграє. Побудована математична модель є надто «ідеальною». Адже в реальності колода досить наближено має форму прямого кругового циліндра. Припущення щодо умови міцності бруса теж можуть відрізнятися від наведених.

ЗАДАЧА. Як визначити діаметр циліндричного стержня, закріпленого з двох кінців, за допомогою штангенциркуля, якщо відома довжина «ніжок»   штангенциркуля, але вони коротші від радіуса стержня?

ЗАДАЧА. На циліндричний стержень щільно намотано дріт в один шар. Як визначити довжину дроту?

ЗАДАЧА. Скільки мідної проводки діаметром 5мм можна прокатати із зливка об’ємом 0,5м³?

ЗАДАЧА. Скільки у зв’язці електродів для електрозварювання, якщо їх загальна маса 10кг, а кожен електрод – кусок сталевої проводки довжиною 45см і діаметром 6мм? Густина сталі 7600кг/м³.

ЗАДАЧА. Знайти об’єм шахтного стовбура діаметром 8м, якщо його глибина 800м.

          ЗАДАЧА. Залізобетонна панель має розміри 600х120х22см. По усій її довжині – 6 циліндричних отворів, діаметри яких 14см. Знайти масу панелі, якщо густина матеріалу 2,5т/м³.

Зрозуміло , що обчислення тут будуть наближені.

Корисно звернути увагу на термінологію. Висоту матеріального тіла не завжди називають висотою. Говорять про довжину проводу, стержня, про глибину ямки, свердловини, про товщину прокладки.

Особливу увагу слід приділити задачам про труби. Є безліч труб – водогінні, опалювальні, газові, каналізаційні, водовідвідні, вентиляційні. На задачах про труби добре ілюструвати і закріплювати формули об’єму і площі поверхні циліндра.

          ЗАДАЧА. Зовнішній і внутрішній діаметри кілька для колодязя відповідно – 1,3м і  1,1м, а висота 0,9м. Скільки кубометрів бетону потрібно для виготовлення 8 таких кілець?

ЗАДАЧА. а)Знайти масу десятиметрової труби діаметром 1420мм, зробленої із сталевого листа товщиною 22мм. Густина сталі 7600кг/м³.

б) Скільки тон таких сталевих труб потрібно, щоб прокласти газопровід Уренгой – Ужгород, довжина якого4451км?

в) Знайти загальний об’єм (внутрішній) газопроводу.

г) Знайти площу поверхні десятиметрової труби діаметром 1420мм.

д) Скільки квадратних метрів ізоляційної стрічки потрібно, щоб двічі покрити нею труби газопроводу?

На місцевому матеріалі можна скласти безліч задач такого типу (розміри труб – стандартні).

Бажано розв’язувати задачі і про рулони (поліхлорвінілова плівка для обмотки газопроводів, папір і кіно- чи фотоплівки). Нерідко виникає потреба дізнатися про площу матеріалу, змотаного у рулон. Це робиться за допомогою формули об’єму циліндра.

ЗАДАЧА. Скільки квадратних метрів паперу у рулоні, висота і радіуси якого відповідно 85см, 45см і 2см, якщо товщина паперу 01мм?

ЗАДАЧА. Висота весільного торта 8 дм, радіус основи 5 дм. Торт розрізали так, що у перерізі утворився квадрат. Знайдіть відстань від цього перерізу до осі.

Конус

Багато фізичних тіл чи їхніх частин мають конічну форму: кінець олівця, «ніс» ракети, дах башти, терикон.

 

Конус одна із фігур, що традиційно використовується в картографічних проекціях. Для більш точного проектування використовують не один конус, а серію зрізаних конусів.

Конуси застосовуються  в архітектурі. Храм – музей св. Софії в Стамбулі, Собор в Вормсі. Германія , Церква Реденторе, Венеція, канал Джудекка  (на фото), побудовані із використанням конуса.

  

   Житло канадських ескімосів.

  Житло селянина в Сірії.

Дах комори для зерна має форму конуса. Такі хижки можна побачити в Буркіна – Фасо.

Вулканічні гори бувають різних видів, розташовані в  різних частинах Земної кулі, утворені за рахунок накопичення лави і обломків гірських порід, які були вивержені через довгі циліндричні жерла.

Гора Арарат, вулкан на Армянському нагір’ї в Турції.  Форма гори – конус.

Гора Фудзіяма в  Японії має форму конуса. Висота 3776 м над рівнем моря. Сплячий вулкан з 1708 року.

Вулкан Атітлан, Гватемала.

Гора Пан-ді-акуар , Бразилія.

Раковина молюска нагадує форму конуса.         

Особливістю конусів є «загостреність», яка є наслідком побудови фігури.

При переході до вивчення конусів варто вказати, що природно насипані на горизонтальній поверхні купи піску, зерна , вугілля, породи мають форму конусів. При цьому кожному сипучому матеріалу відповідає певний кут природного укосу (кут нахилу твірної до площини основи конуса). Так, наприклад, пісок має кут укосу -25⁰, глина – 30⁰, гравій – 33⁰, вугілля – 42⁰, порода -46⁰.

Інші приклади матеріальних конусів: нижня частина заглиблення , зроблена свердлом в металі, верхні частини багатьох нафтосховищ. Форму зрізаного конуса мають відра, тазики, ролики багатьох підшипників.

При вивченні конуса слід розглядати задачі про терикони.

ЗАДАЧА. Скільки тон породи в териконі висотою 90м, якщо відомо, що кут природного укосу породи 46⁰, а її густина 2т/м³?

Куля і сфера

Форму кулі мають як природні об’єкти, так і штучні, створені людиною. Куля і сфера відносяться до числа найбільш симетричних фігур у просторі. Приклади матеріальних куль: кульки підшипника, спортивні ядра, цукерки-драже тощо. Форму наближену до кулі, мають Земля, Місяць, Сонце, інші небесні тіла; ялинкові прикраси і м’ячі.

Багато овочів  , фруктів – мають форму кулі.

Камені для прикрас мають кулясту форму.

      

Аеростати і космічні кораблі – кулястої форми.

  

ВОЛЬВОКС – колоніальна прісноводна зелена водоросль. Колонія має вигляд пустої кулі (діаметром не більше 3мм), поверхня якої утворена клітинами водорості. Допускається, що колоніальні форми такого роду –одна із ланок, які сполучають одноклітинні і багатоклітинні організми.

Певні елементи архітектурних будівель мають форму кулі.

Діаметри   невеликих матеріальних куль вимірюють кронциркулем або штангенциркулем, а якщо потрібна більша точність – мікрометром.

ЗАДАЧА. Чи достатньо знати свій ріст і радіус Землі, щоб наближено визначити, як далеко можна оглянути Землю, стоячи на рівному місці?

ЗАДАЧА. Радіус Землі 6,4тис.км. Який шлях проходять за добу внаслідок обертання Землі міста Одеса, Львів і Київ, широти яких становлять 46⁰29^/, 49⁰49^/, 50⁰27^/?

ЗАДАЧА. Радіус Землі дорівнює 64000км. На яку висоту над горизонтом слід піднятися, щоб лінія горизонту проходила на відстані 100км від спостерігача

ЗАДАЧА. Куля котиться по жолобу , утвореному двома плоскими поверхнями. По якій лінії рухається її центр?

ЗАДАЧА. Як виміряти радіус більярдної кулі?

ЗАДАЧА. М’яч  , радіус якого дорівнює 15см, лежить: 1) біля стіни;2) у куті кімнати. Чи поміститься в утвореному просвіті кулька для настільного тенісу, радіус якої дорівнює 1,5см?

ЗАДАЧА. Що ви обрали б: з’їсти кавун радіусом 10см утрьох чи з’їсти кавун радіусом 20см увісьмох ?

ЗАДАЧА. На базарі продаються кавуни маленькі і великі (за розміром у два рази більші). Вартість маленьких кавунів 1грн., а великих – 3грн. Що вигідніше купити: один великий чи три маленьких кавуни?

Об’єми і площі поверхонь геометричних тіл

Вимірювання геометричних величин (довжин, кутів, площ, об’ємів) є однією із найважливіших задач геометрії.

Застосування геометрії в побуті, виробництві, техніці дуже часто пов’язане з вимірюванням і обчисленням кількісних характеристик тіл. Найважливішими такими характеристиками тіла є його об’єм і площа його поверхні.

Задачі на знаходження об’ємів

Серед геометричних фігур простору виділяють тіла, які моделюють об’ємність фізичних тіл.

          Виробничий  процес гірничої промисловості  відображають наступні  задачі .

ЗАДАЧА. Поперечний перетин польового штреку має форму рівнобічної трапеції, у якої основи рівні 3,4м і 2,6м, а кут при нижній основі рівний 80⁰. Скільки тонн породи  буде в трьох погонних метрах вироблення, якщо об’ємна вага породи рівна 2,2т/м³?

ЗАДАЧА. Довжина лави 220м, посування лінії забою лави за місяць 202,8м. Потужність пласта складає 2,09м. Скільки тонн вугілля складає місячний видобуток вугілля для цієї лави, якщо об’ємна вага вугілля 1,3т/м³?

ЗАДАЧА. Копер скіпового ствола шахти має форму прямокутного

 паралелепіпеда, у якого довжина рівна 5м, ширина 4м, висота рівна 39м.

Скільки листків жерсті буде потрібно для обшивки корпусу  копра, якщо

 розміри листка жерсті 0,7х1,4, а на шви витрачається 1% необхідної

кількості жерсті.

 

 

 

 

 

 

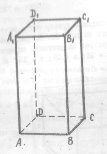
ЗАДАЧА. Приймальний вугільний бункер шахти має форму,зображену на малюнку. За розмірами, вказаними на малюнку , визначити об’єм бункера:

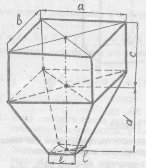а=21, в=21, с=15,d=10, l=3.

 

 

 

                

 

ЗАДАЧА. 260см² мила має масу 410г. Яка маса шматка мила, що має форму прямокутного паралелепіпеда, якщо: а) площа однієї грані шматка складає 96см², площа розрізу через діагоналі обох основ 120см², а діагональ основи (через яку проведено розріз) більша від сторони основи, через яку проходить дана в задачі бічна грань, на 2см; б) бічна поверхня шматка більша площі однієї з бічних граней на 910см²; довжина бічного ребра 20см, периметр основи 62см.  (Відповідь, а) 922г; б) 7656г)

          ЗАДАЧА. Об’єм книги 786м^3, довжина-27см, товщина-2,2см. Яку ширину має книга? (Відповідь.13см)

          ЗАДАЧА.  Для здоров’я учнів необхідно, щоб у класі на кожного учня припадало не менш ніж 6м³ повітря. Клас довжиною 10м, шириною 6м, висотою3,5м. Скільки учнів може знаходитися в ньому без шкоди для здоров’я?    (Відповідь. 35)

      ЗАДАЧА. Глибина класу (відстань від вікон до внутрішньої стіни) не повинна перевищувати 7,1м, щоб віддалені парти були достатньо освітлені. Довжина класу не повинна перевищувати 9,9м, щоб учні, які сидять за задніми партами чітко розрізняли написане на дошці. На кожного учня повинно припадати не менш ніж 6м³ повітря. Беручи до уваги, що повітря вище за 3,6м не бере участь в переміщенні повітряних шарів, обчислити, яка найбільша кількість учнів може одночасно навчатися у цьому класі?   (Відповідь. 42)

ЗАДАЧА. На кожного учня класу має припадати не менше як 6м² повітря. На скільки учнів розрахована класна кімната розмірами 10х6х3,5м?

ЗАДАЧА. Переріз залізничного насипу має вигляд трапеції з основами 18м і 8м та висотою 3м. Знайдіть об’єм 1км такого насипу.

ЗАДАЧА. Правильна шестикутна чавунна  (ρ=7,28г/см³)  призма висвердлена по осі. Її довжина 4,5м, діаметр циліндричного отвору -32см, сторона основи -32см. Визначте масу призми.

ЗАДАЧА. Скільки ящиків , що мають форму паралелепіпеда з розмірами з розмірами   1,4 х1х0,8(м), можна розмістити в контейнері такої самої форми, розміри якого становлять 2,4х3,0х4,2(м)?

ЗАДАЧА. Маса деталі кубічної форми становить 12кг. Знайти масу деталі кубічної форми, зробленої з такого самого матеріалу, якщо її діагональ удвічі більша від діагоналі даної деталі.

ЗАДАЧА. У чавунному бруску вистругано паз. Обчислити масу готової деталі, якщо її розміри вказані на рисунку у мм, а густина чавуну дорівнює 7,5г/см³.

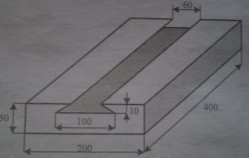
ЗАДАЧА. Зі сталевого бруса, що має форму правильної чотирикутної призми з розмірами  a x a x l, виготовляють дріт циліндричної форми з діаметром d. Знайти довжину виготовленого дроту, якщо а=10см,   l=3,14м, d=2см.

ЗАДАЧА. Скільки важить залізна заготовка, що має вигляд  правильної дванадцятикутної призми, сторона основи якої дорівнює 12см, а висота – 78см? (Питома вага – 7,4т/м³)

          ЗАДАЧА. Знайти вагу залізобетонної балки, довжина якої 6м. Поперечний переріз балки зображено на рисунку (розміри подані у мм). Густина бетону 24кг/м³.

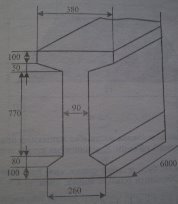
ЗАДАЧА. Бак, що має форму прямокутного паралелепіпеда, доверху заповнено бензином. Довжина бака 3м, ширина 1,5м, висота 1,2м (Розміри внутрішні). Густина бензину 710 кг/м куб. На скільки робочих днів вистачить цього бензину для заправки автомобіля ГАЗ – 53, якщо середні витрати бензину автомобіля за робочий день – 95 кг?

ЗАДАЧА. Відкритий кузов вантажного автомобіля має вигляд прямокутного паралелепіпеда з площею поверхні S. Якими повинні бути довжина і ширина кузова, щоб його об’єм був найбільшим, а відношення довжини до ширини дорівнювало ?

ЗАДАЧА. Цукор-рафінад виготовляють у вигляді шматочків форми прямокутного паралелепіпеда розміром 24х24х10мм. Скільки шматочків цукру повинно міститись у пачці масою 0,5 кг? Питома вага цукру 1,2 г/см².  (Відповідь. ≈70 штук.)

ЗАДАЧА. Конопляне масло, яке перелили в посудину кубічної форми глибиною 7,6см, має масу 411г. Яку масу має 16,4см³ масла? (Відповідь. 15г)

ЗАДАЧА. Коробка для цукерок має форму прямої призми, основою якої є ромб. Бічна поверхня коробки 900см², діагональ дна 40см. Коло, що обкреслює картинку на кришці і дотикається сторін кришки, має довжину 75,36см. Скільки кілограм цукерок може вмістити коробка, якщо 1кг цукерок займає приблизно 2400см²? (Відповідь. 2,2 кг)

ЗАДАЧА. Визначити об’єм пекарної камери (ПХС – 25), якщо її розміри 1,9×0,2×10(м).

ЗАДАЧА. Пекарна камера (ПХС – 25) має форму прямокутного паралелепіпеда. Чому дорівнює її повна поверхня, якщо три її грані мають площі 1м кв., 2м кв., 3м кв.

ЗАДАЧА. Скільки потрібно повидла для прошарування торта, який має форму прямокутного паралелепіпеда розмірами 12х35х20см, якщо на 1см² витрачається 12г повидла?

ЗАДАЧА. Скільки потрібно джему для оздоблення пирога, який має форму три­кутної призми висотою 5см, в основі якої лежить правильний трикутник з сто­роною 20см, якщо на 1см² витрачається 2,5г джему?

ЗАДАЧА. Скільки треба згущеного молока для оздоблення торта, який має форму прямокутного паралелепіпеда розміром 5x20x10см, якщо на 1см² витрачається 5г?

ЗАДАЧА. Скільки потрібно шоколадної помадки для того, щоб оздобити торт, що має форму прямокутного паралелепіпеда розмірами 25x40x45, якщо на 1см² ви­трачається 30г?

 ЗАДАЧА. Яку масу мають 650 цеглин, якщо довжина кожної цеглини 24см, ширина-12см, товщина-5см? ρ=1800кг/м³. (Відповідь. ≈1685кг)

ЗАДАЧА. Скільки цеглин потрібно для кладки 18 стовпів висотою 4м з перерізом у вигляді квадрата зі стороною 7дм? Розмір цеглини1дмх1,5дмх3х дм. Додати 5% на злам. (Відповідь. 13272)

ЗАДАЧА.  Коридор має 21м довжини та 2,1м ширини й уміщує в собі 161м3 повітря. Знайти висоту коридору.  (Відповідь. 3,7м)

          ЗАДАЧА. Кубатура однієї кімнати будівлі дорівнює 120м³. Обчислити кубатуру іншої кімнати, якщо її ширина в 1,5 рази більша від ширини першої, а довжина в 3 рази менша.    (Відповідь. 60м³)

ЗАДАЧА. Для фундаменту кам’яної стіни, що оточує будинок (довжина будинку 383м, ширина-250м) потрібно викопати рів шириною 0,53м і глибиною 36см. За скільки годин зможуть виконати цю роботу 7 землекопів, якщо 3 землекопи за 13 годин викопають 19м³ землі, і якщо три хвіртки мають по 4,3 довжини? (Відповідь. 63 години)

     ЗАДАЧА. Підлога в прямокутному залі викладена мармуровими плитками. Кожна плита має форму правильної 8-кутної призми зі стороною основи 6,4см і товщиною2,5см. Яку площу займає займає підлога, якщо маса всіх плит 89690кг?  (Відповідь. 140м²)

ЗАДАЧА. Стіни та дно прямокутного басейну викладені плитами. Довжина басейну 11м, ширина -6,4м, а глибина -4,3м. Яка маса всіх плит, якщо на 1м² поверхні басейну йде 313кг плит? Товщина плити 13см, а маса 1м³ плити 2352кг. (Відповідь. 469222кг)

ЗАДАЧА. Яка різниця в об'ємі між глиняною звичайною цеглиною 250x120х65мм і модульною 250x120х88мм (силікатною) ?

ЗАДАЧА. Обчислити, скільки цеглин та розчину потрібно завезти до майстерні, щоб побудувати перегородку товщиною в один цегла, довжиною 4м, висотою 2,6м. Відомо, що розміри цеглини 25см на 12см на 6,5см, а на 1м кубічний кладки потрібно – 0,23м кубічних розчину.

  ЗАДАЧА. Потрібно приготувати цементно-вапняний розчин складу 1 : 0,5 : 6. Яку кількість складових компонентів у кубічних метрах необхідно взяти для приготування 1,2м³ розчину?

ЗАДАЧА. Обчислити, скільки розчину піде на штукатурку п’єдесталу (розміри подані в метрах). На 1м³ штукатурки витрачається 18кг розчину.

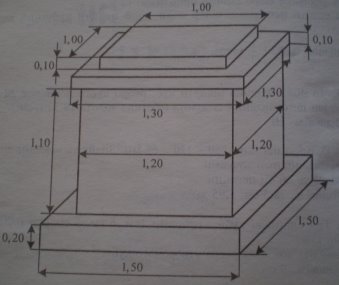
ЗАДАЧА. Розрахувати розхід масляного колектора, що йде на окраску панелі приміщення, розміри якого 4000х5000х3000, якщо на окраску 1 м² потрібно 0,2 кг(вікна і двері займають 12% площі поверхні).

ЗАДАЧА. Ящик для овочів має форму прямого паралелепіпеда, сторони основ 2√2см і 5см утворюють кут 45°. Менша діагональ ящика дорівнює 7см. Знайдіть його об’єм.

ЗАДАЧА. Скільки будівельної цегли і розчину потрібно для побудови стіни довжиною 12 м, товщиною 0,5м, висотою 2,5 м, якщо 1м³ цегляної площадки містить 400 шт цеглин, а потреба в розчині складає 0,2 об’єму кладки?

ЗАДАЧА. Скільки будівельної цегли і розчину потрібно для побудови стіни площею 6м², висотою 3м, якщо 1м³ цегляної площадки містить 400 шт цеглин, а потреба в розчині складає 0,2 об’єму кладки?

 ЗАДАЧА. Ціна діаманта пропорційна квадрату його об’єму. Як вигідніше продавати діамант: цілим чи розпиляним на частини?

ЗАДАЧА. Яка площа поперечного перерізу сталевої рейки, якщо відома маса m одного погонного метра рейки і густина сталі ρ?х

ЗАДАЧА. Деталь, що має форму правильної чотирикутної піраміди, утворює виступ над корпусом. Вершина деталі недоступна. Які вимірювання потрібно зробити, щоб визначити об’єм піраміди?

ЗАДАЧА. З двох дерев’яних колод одна вдвічі товща за другу і вдвічі коротша від неї. Яка з них важча – коротка чи довга?

ЗАДАЧА. Який об’єм молока може вміститися в тетрапак у вигляді піраміди, основа якої рівносторонній трикутник зі стороною 20 см, висотою 24 см.

ЗАДАЧА. Піраміда Хеопса спочатку мала висоту 147м і займала площу 34300м². Скільки тонн речовини потрібно було для облицювання споруди, якщо на 1м² використовували її 160кг?

ЗАДАЧА. Піраміда Хеопса мала висоту 147м², сторона її квадратної основи -230м. Внутрішні ходи і приміщення займають 30% її об’єму. Визначити масу каменю, який пішов на її спорудження. (Маса 1м³ каменю дорівнює 2,5т.)

ЗАДАЧА . Для підсипки під’їзних шляхів до будівельного майданчика завезено гравій, складений в купу (з певною похибкою) правильної чотирикутної піраміди, сторони основ якої 12м, 4м, а висота 3м. Скільки кубічних метрів гравію привезено на будівельний майданчик?

ЗАДАЧА. Фірма одержала замовлення на виготовлення 50 стовпчиків у формі правильної чотирикутної піраміди для огорожі місця, де ведуться дорожні роботи. Відомо, що висота цих стовпчиків має дорівнювати 0,5м, сторона основи – 0,3м. Скільки кілограмів матеріалу для виготовлення стовпчиків необхідно закупити фірмі, якщо 1м² такого матеріалу має масу 2700кг?

ЗАДАЧА. Обчислити пропускну здатність водоперегінного каналу (у м³), якщо його переріз – це круг з радіусом 10см, довжина труби – 5м.

ЗАДАЧА. 1,17кг сталевого дроту діаметром 2,5мм витягнули в дріт діаметром 1,5мм. На скільки збільшилася довжина дроту (ρ=7,8 г/см³)?

ЗАДАЧА. Бетононасос переміщує 15м³ бетону за одну годину. З якою швидкістю бетон переміщається трубою з діаметром 15см ?

ЗАДАЧА. Як обчислити об’єм соснової колоди довжиною: а)1м;б) 10м?

ЗАДАЧА. Довжини двох круглих колод рівні, а їх діаметри відносяться як 2:3. Як відносяться їх об’єми?

ЗАДАЧА. На столі стоїть наполовину заповнена рідиною закрита циліндрична посудина, висота якої Н дорівнює діаметру основи. Чому дорівнює площа вільної поверхні рідини , якщо вісь посудини розміщена горизонтально?

ЗАДАЧА. Циліндричний бак висотою Н і з радіусом R основи на третину заповнено рідиною. Чи поміститься ця рідина в цистерні тієї самої висоти і з удвічі меншим радіусом основи?

ЗАДАЧА. У циліндричній цистерні з горизонтальною віссю вода займає ¾ її висоти. Довжина цистерни 4,8м, діаметр -1,4м. Знайдіть об’єм води у цистерні.

  ЗАДАЧА. Скільки меду можна вмістити в посудину, що має циліндричну форму з діаметром основи 22 см і висотою 46 см, якщо густина меду 1350кг/м³.

ЗАДАЧА. Знайти  об’єм циліндричної склянки, якщо довжина її кола основи 25,1 см,а висота 8 см. Скільки води вона вміщує?

ЗАДАЧА. Скільки повних порцій супу міститься в каструлі, яка має форму циліндра, висота якого 40 см, а діаметр 0,3 м. Відомо, що одна порція містить 0,25 л супу.

ЗАДАЧА. Діаметр каструлі 44 см, а висота 32 см. Скільки літрів води вона вміщує?

ЗАДАЧА. Діаметр зовнішнього корпусу харчо варильного котла дорівнює 1 м, а внутрішнього циліндру – 80 см. Висота котла 1м 20 см. Знайти об’єм пароводяної сорочки цього котла.

ЗАДАЧА. Цистерна для молока має циліндричну форму. Діаметр основи дорів­нює 1,2м. Довжина цистерни - 2м.Скільки літрів молока може вмістити ця цис­терна?

ЗАДАЧА. Скільки кубічних дециметрів (літрів) води вміщає бак, що має форму циліндра, коли радіус його основи дорівнює 30м, висота - 0,6м?

ЗАДАЧА. Закладають в циліндричну каструлю небагато рису. Скільки потрі­бно налити води, щоб вийшла смачна каша ?

ЗАДАЧА. Склянка має форму циліндра з діаметром основи 12 см і висотою 20см. Скільки порцій чаю можна видати, якщо чай готувати в циліндричній ка­струлі радіусом 50см і висотою 80 см ?

ЗАДАЧА. Визначити вагу салату сформованого циліндричною посудиною з твірною 5 см та довжиною кола основи 30 см, якщо 1см³ має вагу 9г.

 ЗАДАЧА. Два торти циліндричної форми, висотою 12см з діаметром основи одного з них 20см , а другого — в 2 рази меншого. У скільки разів один торт ва­жчий за другий?

 ЗАДАЧА. 50л олії зберігалося у бочці циліндричної форми висотою 80 см. Протягом тижня олію використовували для приготування їжі і її рівень зменшився на 30 см. У скільки разів зменшився об'єм олії в бочці?

 ЗАДАЧА. Один кухар взяв каструлю радіусом К, висота якої в 2 рази більша ніж радіус. А другий - каструлю з радіусом 2 К , з висотою у два рази меншою. Хто з кухарів нагодує більше гостей ?

 ЗАДАЧА. Скільки циліндричних бочок заввишки 1,5м і з діаметром основи 0,8м потрібно мати, щоб перелити в них рідину з циліндричної цистерни, довжина якої 4,5м і діаметр основи 1,6м?

ЗАДАЧА. У циліндричну посудину, внутрішній діаметр якої – 20см, опущено деталь. Рівень рідини, яка була в посудині, піднявся на 12см. Знайдіть об’єм деталі.

ЗАДАЧА. Свинцева труба (ρ=11,4г/см³) з товщиною стінки 4мм має внутрішній діаметр 13мм. Знайти масу 25м труби.

ЗАДАЧА. Сталевий вал 1,40м завдовжки і 0,083м у діаметрі обточують на токарному верстаті, причому діаметр його зменшується на 0,003м. Скільки ваги він втрачає в результаті обточування? (Питома вага сталі 7,4г/см³)

ЗАДАЧА. Виявилося, що маркування та технічні дані змішувачів розчину  СО-80 і С-368 стерлася. Які виміри необхідно виконати, щоб розрахувати об’єм розчину в бункері кожного змішувача? Яка з формул в цьому випадку знадобиться:   ?

  ЗАДАЧА. Муляру потрібно покрити поверхню загальною площею 200 кв. м. Внутрішній діаметр резервуару фарбопульту ручної дії приблизно дорівнює 178 мм, висота 715 мм. Відомо, що при дворазовому покритті витрачається 480 г на 1 кв.м. Розрахуйте скільки разів і якою кількістю водяної фарби прийдеться наповнити робочому резервуар, щоб не залишилось залишків.

  ЗАДАЧА. Залізобетонна панель має розміри 600х120х22см. По всій її довжині є 6 циліндричних отворів діаметром 14см. Знайдіть масу панелі, якщо густина залізобетону 2,5т/м³.

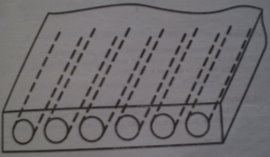
  ЗАДАЧА. Скільки важить погонний метр карниза з вапняку, поперечний переріз якого подано на рисунку. Розміри подано в сантиметрах. (Питома вага пісковику 2,4г/см³)

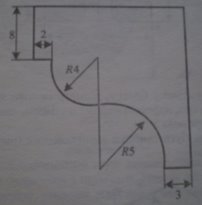
  ЗАДАЧА. На будівництво необхідно завести труби для монтажу мережі водопостачання. У зв’язку із цим треба виконати наступні розрахунки.

  1) Знайти об’єм труби діаметром 60 мм і довжиною 3 м, якщо товщина металу, з якого виготовлена труба, становить 5 мм.

  2) Скільки таких труб можна навантажити на автомобілі ЗИЛ-130 і КамАЗ-5320, якщо вантажопідйомність ЗИЛ-130–6000 кг, а КамАЗ-5320 –8000 кг (густина металу = 7,8 г/см³ = 7800 г/см³).

  3) Кузов автомобіля ЗИЛ-130 має внутрішні розміри 3752 мм × 2326 мм × 575 мм, а розміри кузова КамАЗ-5320 становлять 5200 мм × 2320 мм × 500 мм. Який автомобіль і у скільки разів продуктивніше працюватиме під час перевезення вантажу, якщо час навантаження, транспортування та розвантаження, буде однаковим?

  4) Обчислити витрати палива та його вартість під час перевезення 250 труб вантажними автомобілями ЗИЛ-130 і КамАЗ-5320 на відстань 30 км (ціна 1 л бензину А-80 – 4,80 грн, дизельного пального – 5,05 грн). 

  5) Зварник виконав завдання з монтажу системи водопостачання та виконав 20 стикових швів труб діаметром 60 мм. Який заробіток отримав робітник, якщо плата за виконання 1 м стикового шва становить 42,1 грн?

  ЗАДАЧА. Ролик підшипника кочення має форму циліндра, висота якого 20 мм, діаметр основи 10 мм. Знайти об’єм матеріалу, з якого виготовлено ролик.

ЗАДАЧА. Знайти об’єм пальної суміші в циліндрі автомобіля КамАЗ, знаючи, що внутрішній діаметр циліндра 120 мм, а робочий хід поршня 120 мм.

  ЗАДАЧА. Відро має форму циліндра, діаметр якого 26см, а висота 35 см. Скільки поміститься бензину у відрі, якщо його наповнити доверху?

  ЗАДАЧА. Скільки тонн бензину можна зберігати в цистерні циліндричної форми, якщо її діаметр 4 м, а довжина 3 м? (Густина бензину 700 кг/м³.)

  ЗАДАЧА. Яким повинен бути радіус основи циліндричного бачка висотою 6 м, щоб у нього помістити 50 т бензину (густина бензину 0,7 т/м³)?

  ЗАДАЧА. Рідину, що міститься в циліндричній склянці, діаметр основи якої дорівнює 6см, а висота -9см, треба перелити у конічну посудину висотою 11см і з діаметром 9см. Чи поміститься рідина у конічній посудині?

ЗАДАЧА. Визначити вагу салату поданого у формі конуса з твірною 10 см та довжиною кола основи 40 см, якщо 1см³ має вагу 7г.

 ЗАДАЧА. Відра , які використовують під час гасіння пожежі мають конічну форму. Скільки літрів води вміщує таке відро, якщо його висота дорівнює 0,5м, а діаметр основи – 0,3м. (1л води займає об’єм 1000см³ ).

ЗАДАЧА. Визначити місткість відра, висотою 40см та діаметрами дна і верх­нього перерізу  відповідно 25см і 30см.

Для гірників можуть бути запропоновані задачі такого змісту.

ЗАДАЧА.Поперечний перетин шахтного ствола – круг діаметром 3,5м. Шахта пройдена на глибину 67,6м.  Визначити  об’єм вийнятого ґрунту.

ЗАДАЧА.Визначити кількість повітря, що подається вентилятором місцевого провітрювання в глухий забій гірничої виробки за 1хв., якщо швидкість руху повітря  по  трубопроводу складає 8м/сек, а діаметр трубопроводу складає 0,6м.

           Розглянемо, як приклад задачу, яку можна застосувати на уроці в групі підготовки  за спеціальністю штукатур, лицювальник – плиточник .

ЗАДАЧА. Для бетонування підлоги у їдальні училища привезли пісок. Цю купу піску необхідно перенести у приміщення. Скільки відер необхідно для такого перенесення?

Щоб розв’язати задачу, необхідно оцінити об’єм піску в купі. Як це зробити?

За формою купа піску помітно відрізняється від відомих нам просторових фігур; віддалено вона нагадує круговий конус. Для об’єму конуса маємо формулу:  .

Проте навіть допустивши, купа піску має форму конуса, складно безпосередньо виміряти значення R і H. Можемо вважати, що основою конуса – моделі служить круг, коло якого має таку саму довжину, як периметр основи купи. Цю довжину можемо виміряти безпосередньо шнуром: якщо вона дорівнює С, то . Висоту Н теж важко виміряти безпосередньо, але легко за допомогою шнура знайти довжину «перекидки» : l=AS+SB.

Тоді  .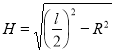

В умові даної задачі йдеться про конкретний сипучий матеріал. При вільному насипанні сипучого матеріалу у вигляді купи, близької за формою до конуса, крутизна не може бути довільною; для кожного сипучого матеріалу кут природного відкосу (кут нахилу твірної до площини основи конуса) свій; для піску він наближено становить 45⁰. Ці дані дозволяють спростити розв’язування  задачі та знайти об’єм купи піску за допомогою лише одного виміру, а саме – довжини «перекидки» l.

Справді,  .

 

ЗАДАЧА. Стаканчик для морозива конічної форми має 12 см глибини і 5 см по діаметру верхньої частини. На нього зверху поклали дві ложки морозива у вигляді півкулі діаметра 5 см. Чи переповнить це морозиво стаканчик, якщо дозволити йому розтанути?

ЗАДАЧА. Картоплю насипали в купу конічної форми. Довжина кола основи купи 12м, твірна -3м.Скільки тонн картоплі знаходиться в купі? Маса 1м³ картоплі 800 кг.

ЗАДАЧА. Суміш гравію з піском у вигляді конічної кучі , твірна якої 2,1м довжина кола основи конуса С = 6,28м. Якою повинна бути вантажопідйомність вантажної машини, щоб перевезти цю суміш, якщо 1 м куб. суміші має 1600 – 1900 кг ?

ЗАДАЧА. Які вимірювання й обчислення доцільно зробити, щоб знайти масу купи щебню, яка має форму конуса?

ЗАДАЧА. Купа піску має форму конуса, довжина кола основи якої дорівнює 25м, а довжина твірної-5м. Скільки  ходок тритонної машини потрібно для його перевезення, якщо маса 1м³ піску дорівнює 2т?

ЗАДАЧА. Пісок насипано в конічну купу так, що крутизна укосини дорівнює 1:1,5. Довжина кола основи – 4м. Визначити об’єм кути.

ЗАДАЧА. Купа щебню має форму конуса, твірна якого – 4м. Знайдіть її об’єм, якщо кут природного укосу для щебню – 30⁰.

ЗАДАЧА. Розчин висипали у вигляді конічної кучі, твірна якої 6,3м, довжина кола С = 17,6м, чи вистачить його для кладки 190м³  стінки, якщо для кладки 1м³   стінки потрібно 0,23м³   розчину ?

ЗАДАЧА. Маємо два конуси однакового зерна одного сорту: один удвічі вищий за другий. У скільки разів у першому конусі більше зерна, ніж у другому?

ЗАДАЧА. Рідина, яка заповнює конічну посудину висотою 0,18м і з діаметром основи 0,24м, переливається в циліндричну посудину з діаметром основи 0,1м. Як високо буде знаходитися рівень поверхні рідини в циліндричній посудині?

ЗАДАЧА. У дворі має працювати невеликий фонтан. Вода налита в посудину конусовидної форми заввишки 0,18м із діаметром основи 0,24м, переливається в циліндричну посудину, діаметр основи якої 0,1м. На якій висоті розміщено рівень рідини в циліндричній посудині?

ЗАДАЧА. Копиця сіна має форму прямого кругового циліндра з конічним верхом. Довжина кола основи циліндра дорівнює 20,5м, висота копиці-4м, а висота її циліндричної частини-2,2м. Знайдіть масу сіна, якщо його густина 0,03г/см³.

ЗАДАЧА. Скільки тонн породи містить терикон конічної форми з твірною 0,2км, якщо кут його схилу дорівнює 46⁰, а густина породи-2т/м³?

ЗАДАЧА.  За розмірами, даними на малюнку (а=5м, в=1м, с=6м,D=4м)   визначити об’єм вугленавантажувального бункера, що має форму комбінації циліндра і зрізаного конуса.

 

 

 

 

 

 

 

 

ЗАДАЧА. Визначити , скільки залізничних платформ вантажо-підйомністю 25т потрібно для перевезення конусоподібної купи вугілля, заввишки 7,5м. об’ємна вага вугілля рівна 1,3 т/м³.

ЗАДАЧА. Купа піску має форму конуса, довжина кола основи якого дорівнює 25,12 м, а твірна – 5 м. Скільки автомобілів вантажопідйомністю 3 т потрібно для її перевезення, якщо маса 1 м³ становить 2 т?

ЗАДАЧА. Ролик радіально-опорного підшипника має форму зрізаного конуса з діаметрами основ 5 мм і 6 мм та висотою 7 мм. Знайти об’єм матеріалу, з якого виготовлено ролик.

ЗАДАЧА. Скільки літрів води вміщує відро, що має форму зрізаного конусу, якщо діаметри його основ дорівнюють 28 см і 24 см, а твірна – 24,5 см?

ЗАДАЧА. Цинкове відро має форму зрізаного конусу з діаметрами основ 31 см і 22 см та твірною 27 см. Скільки матеріалів пішло на його виготовлення, якщо на шви та відходи йде 12%?

ЗАДАЧА. Завантажувальна лійка картоплечистки МОК-16 має форму зрізаного конусу. Обчислити площу її бічної поверхні, якщо радіус більшої основи дорівнює 16 см, радіус меншої основи – 9см, довжина твірної – 10 см.

ЗАДАЧА. Тістомішалка має форму зрізаного конуса, у якого радіуси основ 4см і 22см, а борошносіялка - циліндричної форми. Вони мають одну і ту саму висоту та об’єм. Чому дорівнює радіус основи борошносіялки ?

 ЗАДАЧА. Бак має форму зрізаного конусу, радіуси основи якого дорівнюють 30 см і 20 см, а висота 24 см. Визначте об’єм цього баку.

ЗАДАЧА. До витяжної труби необхідно приробити ковпак у вигляді зрізаного конуса, висота якого 30см і діаметри основ 100 і 20см. Скільки квадратних метрів листового заліза потрібно для його виготовлення , якщо на шви необхідно додати 2%?

ЗАДАЧА. Над котлом зробили ковпак у формі зрізаного конуса, розміри якого (у метрах) подано на рисунку. Скільки квадратних метрів листового заліза пішло на його виготовлення? (Обрізки не беруться до уваги)

Об’єм кулі

Суспільство потребує як талановитих дослідників, так і спеціалістів, які добре знають математику та здатні застосовувати свої знання на практиці.

Математичні ідеї та методи все більше використовуються в найрізноманітніших галузях наук і практичній діяльності людини. Без математики не обійшлися під час виведення на орбіту штучних супутників Землі, створюючи супутники зв’язку, навігаційні супутники. Математику використовують у космічній метеорології.

ЗАДАЧА. 12квітня 1961 року світ захоплено слухав повідомлення ТАРС: «12 квітня 1961 року у Радянському Союзі виведено на орбіту навколо Землі перший у світі космічний корабель-супутник «Восток» з людиною на борту. Льотчиком-космонавтом космічного корабля –супутника «Восток» є громадянин Союзу Радянських Соціалістичних Республік, льотчик, майор Юрій Олексійович Гагарін. Період обертання корабля-супутника навколо Землі – 89,1 хв; мінімальна відстань від поверхні Землі дорівнює 175км, а максимальна відстань -302км…».  

Знайти об’єм частини земної кулі, поверхню якої бачив Ю.О.Гагарін.

     ЗАДАЧА. Редукційний клапан двигуна автомобіля ГАЗ 53 має форму кулі діаметром 8 мм. Знайти об’єм клапана.

   ЗАДАЧА. Маса кульки дворядного сферичного підшипника дорівнює 3 г. Який її діаметр    (p=7,8 г/см³)?

  ЗАДАЧА. Як обчислити радіус металевої кульки, скориставшись лінійкою і прозорою циліндричною посудиною з водою?

ЗАДАЧА. Чавунний зливок має форму двох куль, з’єднаних циліндричним стержнем. Діаметри куль 12см, відстань між центрами-30см, діаметр циліндричного стержня-4см. Визначте масу зливка (ρ=7,2г/см³).

  ЗАДАЧА. Пересипаючи пісок з порожнистої півкулі радіуса r у конус,  радіус і висота якого дорівнюють  r , учень дійшов висновку, що об’єм півкулі у 2 рази більший за об’єм конуса. Чи відповідає результат цього експерименту теорії?

ЗАДАЧА. За замислом архітектора вхід до Палацу молоді мають прикрашати дві кулі діаметром 0,8м, які розміщено по обидва боки від сходів. Ці кулі виготовляють із природного каменю , густина  якого дорівнює 4,5х10³кг/м³. Чи можна обидві виготовлені у майстерні кулі доставити до місця будівництва на одній вантажівці, вантажопідйомність якої дорівнює 3т?

ЗАДАЧА. Резервуар для води складається з півкулі, радіус якої дорівнює 14дм, і циліндра, основа якого має такий самий радіус. Яку висоту має циліндрична частина, якщо резервуар містить 12000л води?

ЗАДАЧА.  Що вигідніше: купити кавун радіусом 30см або три кавуни радіусом 10см?

  ЗАДАЧА. Що б ви вибрали: удвох з’їсти кавун з радіусом 10см, чи вдесятьох – кавун, радіус якого складає 20см?

  ЗАДАЧА. Діаметр одного кавуна вдвічі більший за діаметр другого. У скільки разів перший кавун важчий за другий?

ЗАДАЧА. Котел, що має форму півкулі, вміщує 28.6л води. Визначити діаметр котла.

ЗАДАЧА. Водій отримав завдання перевезти землі для клумби, що має форму сегменту кулі з радіусом 5м, і висотою 60 см. Скільки кубометрів землі потрібно для облаштування клумби?

ЗАДАЧА. На будівельному майданчику знаходиться ємкість для води у формі сегменту кулі з радіусом 2м і висотою 1 м. Скільки кубометрів води вміщується в цю ємкість?

ЗАДАЧА.  Студент купив в магазині гарну чашку у формі сегменту кулі і хоче дізнатися, який її вміст. Він виміряв діаметр чашки і висоту, які дорівнюють відповідно 15 см і 7 см. Знайти об’єм чашки.

Площі поверхонь геометричних тіл

ЗАДАЧА. Визначити площу керамічної плитки й кількість плитки, необхідної для обкладання підлоги, що має форму шестикутника , розміром 2,3х3,1м, якщо плитка має форму правильного шестикутника зі стороною: а=0,25м.

Розв’язання

1.Для обчислення площі плитки використаємо формулу для обчислення площі правильного шестикутника:

2.Визначити площу підлоги:

2,3х3,1=7,13(м²).

3. Визначити необхідну кількість плитки:

Відповідь. Для обкладання підлоги необхідно не менше 99 плиток.

 

Задачі на обчислення площі поверхні призми

ЗАДАЧА. Коробка для упаковування подарунка має форму низької призми із ромбом в основі. Найбільша відстань між протилежними кутами кришки 24см, а найменша-10см. Висота коробки 4см. Скільки потрібно квадратних сантиметрів кольорового паперу, щоб обклеїти коробку (крім дна)?

ЗАДАЧА. Для обклеювання тільки з боку іншої, але такої ж за формою коробки, яка має висоту 5см і відстань між двома протилежними кутами 10см, використали 260см² паперу. Скільки необхідно паперу для обклеювання кришки?

ЗАДАЧА. За умовою задачі у (1) визначте площу перегородки із картону, яка проходить усередині коробки між найближчими її кутами і між більш віддаленими кутами, а також периметр кришки.

ЗАДАЧА. Результати обчислень попереднього випадку візьміть за умову та визначте кількість паперу, потрібного для обгортання коробки, якщо для цього витрачено паперу на 30% більше, ніж для обклеювання всієї коробки.

ЗАДАЧА. Складіть ще задачу (візьміть із основної задачі дані на вибір). (Відповідь. 1) 328см²; 2) 120см²; 3) 96см²; 40см².)

ЗАДАЧА. Для виготовлення квадратного ящика висотою 80см без кришки і дна використали дошку довжиною 6,4м і шириною 4,3м. Скільки таких дошок піде на дно та кришку? На відходи додати половину дошки. Як сформулювати цю задачу, використовуючи лише геометричні терміни? (Відповідь. ≈6 дошок)

ЗАДАЧА. Для відправлення товарів виготовлено 80 кубічних ящиків довжиною по 106см. Скільки дошок пішло на ящики, якщо на 1м² ящика потрібно приблизно 1 дошку? Дошка має довжину 496см, а ширину-222см. (Відповідь. 535 дошок)

ЗАДАЧА. Чи можна дерев’яний куб з розмірами 1х1х1(дм) загорнути в квадратну хустку розмірами 3х3(дм)?

ЗАДАЧА. Прямокутна кімната довжиною 5,6м, шириною 3м і висотою 2,5м обклеєна шпалерами. В кімнаті є вікно шириною 2,3м і висотою 1,3м та 2 дверей шириною по 1,1м і висотою 2,1м. Скільки потрібно мати рулонів шпалер, якщо довжина кожного рулону 10м і ширина 53см? (Відповідь. ≈7)

ЗАДАЧА. Для оклеювання шпалерами стін кімнати використано 93,5м² шпалер. Вікна та двері займають 15,1м². Бордюр, яким обклеєні шпалери вздовж всіх стін, має довжину 25,5м. Скільки буде коштувати фарбування підлоги цієї кімнати, якщо за фарбування олійною фарбою кожного квадратного метра беруть 3 гривні і якщо висота кімнати менша від її ширини на 1,42м?  (Відповідь.121 гривень.)

ЗАДАЧА. Потрібно зацементувати підвал глибиною 2м, шириною 2,5м і довжиною 4м. Скільки потрібно використати для цього пудів цементу, якщо на кожний квадратний метр дна йде 2 пуди, а на квадратний метр стіни – 0,8 пуда цементу? (Підвал має форму прямокутного паралелепіпеда). Міра. 1 тонна = 61 пуд. (Відповідь. 668 кг.)

ЗАДАЧА. Двосхилий дах має форму 3-гранної призми; дах простягається уздовж будинку на 21м, ушир – 8,5м, а висота даху (підйом) – 3,2м. Скільки м² займає поверхня даху? (Відповідь. 227м².)

ЗАДАЧА. Прямокутника садиба, довжиною 153м, шириною 115м, обнесена парканом, який має висоту 213см. За скільки часу 4 малярі зможуть пофарбувати з двох стін паркан з воротами та хвірткою, якщо 1 маляр фарбує за день 40,9м² паркану? (Відповідь.14 днів.)

ЗАДАЧА. Стайня довжиною 17м, шириною 11м, висотою від землі до даху – 496см, зроблена із цегли. В стайні знаходяться: 2 дверей висотою по 284см, шириною 195см; 6 вікон шириною по 709см, висотою по 355см. Скільки пішло цегли на стіни стайні, якщо на 1м² стіни потрібно198 штук цегли?  (Відповідь. 52500штук.)

ЗАДАЧА. Проектується квартира з двох кімнат однакової ширини. Довжину першої хочуть зробити в 1.5 рази більшу віл її ширини, а довжину другої кімнати 7.2м. Знайти ширину кімнат, якщо площа двох кімнат повинна дорівнювати 56,7 м².

ЗАДАЧА. Скільки треба рулонів шпалер розміром 10x0,5м. щоб обклеїти кімнату розміром 6x4.8x3.75? Кімната має 4 вікна розміром 1,8х0,75м. На підклейку витрачається 1% площі шпалер.

ЗАДАЧА. У кімнаті, що має форму прямокутного паралелепіпеда, є два вікна та одні двері. Скільки рулонів шпалер(без малюнка) потрібно придбати, щоб обклеїти стіни цієї кімнати, якщо відомі розміри (у м): кімнати:4х5х2,8; вікон – 1,2х1,8; дверей – 0,9х2,1; рулона – 0,510. Врахуйте, що відходи становлять 5%.

ЗАДАЧА.  Кімната має форму прямокутного паралелепіпеда з розмірами 5,2м на 6,3м на 2,7м. В кімнаті є двоє вікон розмірами 1,2м 1,8м. Обчислити скільки квадратних метрів необхідно обштукатурити, коли штукатурять тільки стіни ?  

ЗАДАЧА. Чи можна використовувати формулу площі бічної поверхні призми для знаходження витрат: а) розчину, який іде на побілку стелі і стін; б) плиток, які потрібні для покриття цоколя житлового приміщення. Відповідь обґрунтувати.

ЗАДАЧА. Скільки тонн розчину треба приготувати для зовнішнього оштукатурення будинку, довжина якого дорівнює 37м, ширина-10м, висота-13м, якщо на втрати розчину досить мати запас, необхідний для оштукатурення площі, яка дорівнює площі вікон і дверей? На 1м² поверхні витрачається 20кг розчину.

ЗАДАЧА. При недотриманні норми товщини штукатурки допускається перевитрата сировини і грошей. Підрахуйте, на скільки збільшиться вартість штукатурних робіт при обробці стін приміщення (довжина-4м, ширина-5м, висота-3м), якщо товщину штукатурки збільшити на 2мм? на 5мм?(Примітка: вартість 1мм штукатурки на 1м² становить ______)      

ЗАДАЧА. Скільки годин потрібно маляру для окраски панелі висотою 2м в приміщені(дані попередньої задачі) щіткою і валиком , якщо норма часу для окраски 100м² поверхні щіткою -6,4год, валиком -3,4год.?

ЗАДАЧА. Скільки дошок завдовжки 4,5 м і завширшки 0,125 м потрібно для виготовлення підлоги в кімнаті розмірами 4.5 х 3.5 м ?

ЗАДАЧА. Кабінет мас розміри 6,5х4.8м і висоту 2.7м. Скільки листів дерево плити розміром 1,2x1.5м потрібно, щоб виготовити панелі, висота яких 1.2м? Двері мають ширину1.5м.

ЗАДАЧА. Знайти площу пофарбованої поверхні і витрати олійної фарби при пофарбуванні дерев'яного   ящика   розміром   по   зовнішньому   виміру 5.8x2.5x1.7 і по внутрішньому виміру 5,6x2.5x1,5м. Фарбування робиться з двох боків по два рази (якщо без кришки). На 1м² витрачається 160 г фарби.

ЗАДАЧА. Потрібно обклеїти шпалерами кімнату розміром 5х4хЗм. Площа вікон і дверей складає 20% всієї площі стін. Скільки потрібно рулонів шпалер для обклеювання, якщо в рулоні 9м і ширина його 500мм?

ЗАДАЧА. Ребра упаковки соку, який має форму прямокутного паралелепіпеда, дорівнюють 6см, 9см і 20см.

1. Знайти загальну площу матеріалу, використаного для виготовлення однієї упаковки, нехтуючи витратами на склеювання.
2. Який об’єм соку в такій упаковці?

ЗАДАЧА. Просіювач борошна – бурат має призматичне сито, площа його основи дорівнює 20 м кв., площа повної поверхні 730 м кв. Під час роботи воно пошкодилось. Вирахувати площу пошкодженої частини сита за умови, що призма правильна шестикутна, та коли воно виходить з ладу, то пошкоджується лише одна грань.

ЗАДАЧА. Поперечний переріз каналу – трапеція (без верхньої основи) з нижньою основою (дном) і бічними сторонами (стінками) довжиною а . При якій величині кута між дном і стінками каналу його пропускна спроможність буде найбільшою?

ЗАДАЧА. Канавокопач риє тимчасові зрошувальні канали трикутного профілю глибиною 0,3м і шириною у верхній частині 0,9м. Визначте довжину каналу, проритого за 1 годину роботи, якщо за цей час машина виймає 75м³ землі.

ЗАДАЧА. Дах башти має форму правильної чотирикутної піраміди. Сторона основи піраміди дорівнює 1,8м, висота-1,2м. Скільки листового заліза потрібно для покриття даху, якщо на суміщення листів припадає 10% площі поверхні покрівлі?

ЗАДАЧА. Дах має форму правильної чотирикутної піраміди, ребро основи якої дорівнює 5м, а бічна грань нахилена до площини основи під кутом 45⁰. Скільки фарби потрібно, щоб пофарбувати цей дах двічі, якщо на одноразове покриття цією фарбою 1м² витрачається 150г?

ЗАДАЧА. Форма для сирної паски (правильна 4-кутна зрізана піраміда) складається з 4 бічних дощечок, з’єднаних гачками, дна і дощечки, на яку ставлять гніт. Визначити висоту форми, якщо площа бічних дощечок становить 1700см², площа усіх дощечок -2376см², а висота бічної дощечки – 25см.

ЗАДАЧА. Потрібно поштукатурити дві колони однакової висоти, але з різним поперечним перерізом : круглим і квадратним. Зовнішній діаметр круглого перерізу і сторона зовнішнього квадрату дорівнюють 30см. На яку колону витратиться більше штукатурки і у скільки разів?

Для майбутніх кравців певні завдання вказують на роль математики у майбутній професії.

ЗАДАЧА. У швацьку майстерню надали заказ на виготовлення чохлів до диванних валиків, довжина валика 80см, а діаметр 24см. Скільки квадратних метрів меблевої тканини потрібно для пошиву 10 чохлів, якщо на залишки від крою відходить 15% тканини?

ЗАДАЧА. Знайти висоту та радіус циліндричної частини капелюха, який має найбільшу площу бокової поверхні, якщо периметр осьового перерізу дорівнює 2р.

ЗАДАЧА. Дві диванні подушки валики одягають в чохли. Довжина одного валика в 2 рази більше другого, але радіус цього основи вдвічі менше другого. На який чохол пішло більше тканини?

ЗАДАЧА. Скільки квадратних метрів тканини необхідно для пошиття намету діаметром основи 4м і висотою 3,5м?

ЗАДАЧА. Знайдіть площу круглої плями на поверхні моря, утвореної 1м³ нафти, якщо товщина її плівки дорівнює 1мм.

ЗАДАЧА. Скільки квадратних метрів бляхи використано для виготовлення одного мільйона банок з діаметром основи 10см і висотою 5см, якщо відходи матеріалу становлять 10%?

ЗАДАЧА. Циліндричний бак , який лежить горизонтально і на третину вкопаний в землю, треба пофарбувати. Як визначити обсяг роботи і необхідну кількість фарби?

ЗАДАЧА. Відро циліндричної форми має діаметр основи 25см і може вмістити 10л води. Скільки жерсті пішло на його виготовлення , якщо на шви  і відходи йде 10% матеріалу?

ЗАДАЧА. Бак циліндричної форми вміщує V  літрів води. Якими повинні бути його розміри, щоб поверхня бака без кришки була найменшою?

ЗАДАЧА. Висота консервної банки циліндричної форми дорівнює 4см, а радіус основи – 6см. Скільки таких банок можна виготовити з 15000м², якщо 10% матеріалу іде на відходи?

ЗАДАЧА. Просіювач борошна – бурат має циліндричне сито, діаметр площі його основи дорівнює 4м, площа повної поверхні 37,68м кв. Під час роботи сито пошкодилось. Вирахувати площу пошкодженої частини сита (це буде площа бічної поверхні циліндра).

ЗАДАЧА. Діаметр циліндричного парового котла завдовжки 3,8м дорівнює 0,8м. Знайдіть тиск пари на повну поверхню котла, якщо на 1см² пара давить із силою 10кГ.

ЗАДАЧА. Скільки квадратних метрів жерсті піде на виготовлення ринви завдовжки 5м і діаметром 20см, якщо на шви додають 3% її площі?

ЗАДАЧА. Чи вистачить 8500м² ізоляційної стрічки для дворазового покриття нею кілометра газопроводу діаметром 1420мм?

ЗАДАЧА. На вулицях міста встановили тумби циліндричної форми для розклеювання реклами. Чи поміститься реклама продукції деякої фірми на одній такій тумбі, якщо загальна площа її рекламних плакатів 5м², а висота та діаметр тумби відповідно дорівнюють 2м і 0,8м?

 ЗАДАЧА. Скільки квадратних метрів паперу в рулоні, висота якого – 85см, а радіуси – 45см і 2см? Товщина паперу – 0,1мм.

ЗАДАЧА. Лійка має форму конуса, утвореного з кругового сектора, радіус якого дорівнює 8см, а центральний кут-60⁰. Знайдіть площу бічної поверхні лійки.

ЗАДАЧА. З листа заліза вирішено зробити відро у формі конуса з діаметром основи 40 см і висотою 60 см. Скільки потрібно заліза? (Припуск заліза на шов – 0,6см)

ЗАДАЧА. Для прикрашання будови магазину на його даху був встановлений козирок у формі конусу. Необхідно визначити, скільки потрібно, скільки потрібно фарби, якщо козирок має діаметр основи 2м і висоту 90 см, а на 1 м витрачається 200 г фарби.

ЗАДАЧА. Силосна башта має конічний дах, висота якого дорівнює 2м, а діаметр основи-6м. Скільки листків бляхи потрібно для покриття даху, якщо розміри листа - 0,7х1,4м, а відходи становлять 10%?

ЗАДАЧА. За замислом архітектора будівлю котеджу прикрашають дві вежі, дах яких має форму конуса. Висота даху – 4м, а діаметр вежі – 6м. будівельна фірма одержала замовлення на покриття дахів черепицею. Скільки листків  черепиці необхідно для покриття цих дахів, якщо один лист черепиці має розміри 0,1мх0,3м?

ЗАДАЧА. Скільки жерсті витрачено на виготовлення 10 відер, висота кожного з яких дорівнює 42см, а діаметри основ – 28см і 34см? (На шви і відходи йде 12% матеріалу).

ЗАДАЧА. Скільки шкіри потрібно для виготовлення покришки м’яча з діаметром 0,3м, якщо відходи матеріалу становлять 10%?

ЗАДАЧА. З краплини мильного розчину діаметра 6мм хлопчик видув бульбашку діаметра 30см. Знайдіть товщину плівки цієї бульбашки.

ЗАДАЧА. Приміщення виставки має вигляд півкулі, площа сферичної поверхні якої - 392πм². Визначте діаметр підлоги.

ЗАДАЧА. Для фарбування круга радіуса 1м потрібно 20г фарби. Скільки такої фарби потрібно, щоб пофарбувати кулю діаметром 1м?

ЗАДАЧА. Для фарбування кулі діаметром 2дм потрібно 30г фарби. Скільки фарби потрібно для фарбування кулі діаметром 6дм?.

Комбінації тіл

Вище було розглянуто властивості найпростіших геометричних тіл: призм, пірамід, циліндрів, конусів, куль. Але багатьом спеціалістам часто доводиться мати справу ізскладнішими тілами, які є різними комбінаціями (об’єднаннями) названих тіл. Ливарникам, формувальникам, фрезерувальникам, електрозварникам, токарям, слюсарям та іншим робітникам доводиться створювати деталі складних конфігурацій.

Свічки запалювання

Блок шестерень

Шпиндель

               Втулка заднього колеса

            Кулачковий  механізм

           Бетонозмішувачі

 

Електродрель багатоцільвого призначення

Бляхарський молоток

Відвіс

Молоток

Гайки, болти

 

ВитяжкаБлендер

    

Набори посуду

      

           Торти – кулінарні шедеври

ЗАДАЧА. Паровозне депо має на плані виглядпівкільця, внутрішній діаметр якого дорівнює 20м. Ширина півкільця – 9м. У поперечному перерізі депо має вигляд прямокутної трапеції ABCD, паралельні сторони якої дорівнюють 4,25м і 6,5м. Знайти об’єм депо.

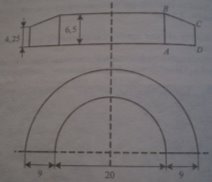
ЗАДАЧА. Знайти кут підйому гвинтової  лінії , якщо зовнішній діаметр D гвинтової нарізки 50мм, внутрішній діаметр d – 42мм, крок гвинта  h - 6мм.

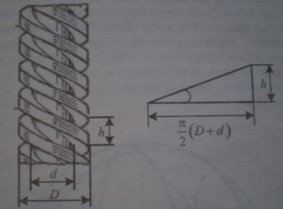
ЗАДАЧА. На  рисунку зображено два тіла, розміщених під прямим кутом один до одного і сполучених за допомогою конічних шестерней. Обчислити кути  х і у нахилу зубців шестерней до осей валів, якщо діаметр однієї шестерні 48см, другої – 32см.

ЗАДАЧА. Будуючи елітне житло, дах будинків прикрашають у вигляді куполів різних форм. Необхідно обчислити поверхню одного з  них, зображеного на рисунку, якщо відомі такі дані: в основу півкулі вписано квадрат, через сторони якого проведено площини, перпендикулярні до площини основи півкулі; ці площини відрізують від півкулі чотири кульові півсегменти; частина, що залишилася, має форму склепіння; сторона квадрата а=6,5м.

ЗАДАЧА. Стаканчик для морозива конічної форми має глибину 12см і діаметр верхньої частини 5см. У нього поклали 2 ложки морозива у вигляді півкуль діаметром 4см. Чи переповнить морозиво стаканчик?

 

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Бевз Г.П. Геометрія в загальноосвітній школі/ Г.П.Бевз//Математика в школах України.-2003.-№1.- с.18.

2. Возняк Г., Маланюк М. Взаємозв'язок теорії з практикою в процесі вивчення математики. — К.: Рад. шк., 1989.

3. Волосюк О.В., Онопченко С.В. Педагогічні аспекти прикладної спрямованості шкільного курсу математики.//Вісник ЛНУ імені Тараса Шевченка. – 2010. – № 17 (204). – С.36-40.

4. Возна М. Спроби формування цілісної картини навколишнього світу в процесі навчання математики// Математика в школах України.-2005.-№30.

5. Державний стандарт базової і повної середньої освіти //Математика в школі.-2004.-№2.

6. Збірник тестових завдань з математики для абітурієнтів / В.І.Беспальчук, А.В.Прус, І.А.Сверчевська та ін.; Під. ред. В.В.Михайленка. – Житомир: ЖДТУ, 2005. – 196с. 

7. Коваль В.В.Прикладна спрямованість шкільного курсу математики//Теорія та методика навчання математики, фізики, інформатики:Збірник наукових праць: В 3-х томах.-Кривий Ріг:Видавничий відділ КДПУ, 2001.-Т.1: Теорія та методика навчання математики.-с.142-148.

8. Кушнір Г.А. Драма геометрії//Математика в школах України.-2004.-№8

9. Лук’янова С.М. Роль прикладної спрямованості в навчанні математики учнів 5-6 класів. // Didactics of mathematics: Problems and Investigation. – Issue#28. – 2007. – С.222-227.

10. Панішко Ф. В. Три половини. Математична наука   // Математика. — № 7 (211).-2003.

11. Порджерс А. «Саймон Флегг і диявол» // Квант. — 1972. - № 8.

12. Прус А.В. Вибрані питання прикладної спрямованості шкільного курсу стереометрії // Дидактика математики: проблеми і дослідження: Міжнародний збірник наукових робіт. - Донецьк: Фірма ТЕАН, 2004. – Вип.22. - С.126-131.

13. Прус А.В., Швець В.О. Дискурсивні висновки щодо прикладної спрямованості шкільного курсу стереометрії на основі генезису вказаного поняття // Дидактика математики: проблеми і дослідження: Міжнародний збірник наукових робіт. – Донецьк: Фірма ТЕАН, 2003. – Вип.20. - С. 126-135. 

14.   Прус А.В. Евристичне навчання та прикладна спрямованість шкільного курсу стереометрії // Эвристическое обучение математике: Тезисы докладов научно-методической конференции (15-17 ноября 2005г.). - Донецк: Изд-во ДонНУ, 2005. – С. 98-99.

15. Прус А. Піраміда в контексті прикладної спрямованості шкільного курсу стереометрії // Математика в школі. – 2005. – №2. - С. 11-15.

16. Прус А.В. Планування у контексті прикладної спрямованості шкільного курсу стереометрії // Підготовка вчителя у контексті Європейського освітнього простору: Збірник наукових праць. – Київ - Житомир: Вид-во ЖДУ імені Івана Франка, 2005. - С. 88-96.

17. Прус А.В. Про засіб прикладної спрямованості шкільного курсу стереометрії // Науковий часопис НПУ імені М.П. Драгоманова. Серія №2. Комп'ютерно-орієнтовані системи навчання: Зб. наукових праць. – К.: НПУ імені М.П. Драгоманова, 2006. - №4(11). – С. 176-181.

18. Прус А.В. Про засоби здійснення прикладної спрямованості шкільного курсу стереометрії // Вісник Житомирського державного університету імені Івана Франка. – Житомир: Вид-во ЖДУ імені Івана Франка, 2005.–– Вип. 20. - С. 100-103.

19. Прус А.В. Про прикладні задачі шкільного курсу стереометрії // Матеріали Всеукраїнської науково-методичної конференції "Проблеми математичної освіти" (ПМО - 2005), м. Черкаси, - Черкаси: Вид. від ЧНУ ім. Б.Хмельницького, 2005. – С. 126-129.

20. Прус А. Про прикладну спрямованість матеріалу, пов'язаного із вивченням призми // Математика в школах України. – 2005. – №13(97). - С. 1-8.

21. Прус А.В. Про прикладну спрямованість шкільного курсу стереометрії // Вісник Житомирського державного університету імені Івана Франка. – Житомир: Вид-во ЖДУ імені Івана Франка, 2003.–– Вип.13. - С. 45-47.

22. Прус А. Про циліндр у контексті прикладної спрямованості // Математика в школі. – 2005.-– №5. – С. 15-20.

23  Прус А.В. Тема "Куля" в контексті прикладної спрямованості шкільного курсу стереометрії // Дидактика математики: проблеми і дослідження: Міжнародний збірник наукових робіт. - Донецьк: Фірма ТЕАН, 2003. – Вип.21. - С. 85-91.

24. Прус А.В. Чинники прикладної спрямованості шкільного курсу стереометрії // Науковий часопис НПУ імені М.П. Драгоманова. Серія №3. Фізика і математика у вищій і середній школі: Зб. наукових праць – К.: НПУ імені М.П. Драгоманова, 2004. - №1. – С. 41-45.

25.Саломатнікова О. Застосування похідної до розв’язування прикладних задач// Математика в школах України.-2005.-№30.

26.Слобода І.В.Математичне моделювання в процесі розв’язування текстових задач// Теорія та методика навчання математики, фізики, інформатики: Збірник наукових праць: В 3-х томах.-Кривий Ріг:Видавничий відділ КДПУ, 2001.-Т.1: Теорія та методика навчання математики.-с.285-289.

27.Смирнова И., Смирнов В. Профильное обучение геометрии: традиции и современность// Математика .-2004.-№12

28.Соколенко Л.О., Філон Л.Г., Швець В.О. Прикладні задачі природничого характеру в курсі алгебри і початків аналізу:практикум. Навчальний посібник. – Київ:НПУ імені М.П.Драгоманова, 2010. – 128с.