Презентація до уроку "Вступ до стереометрії"
Про матеріал
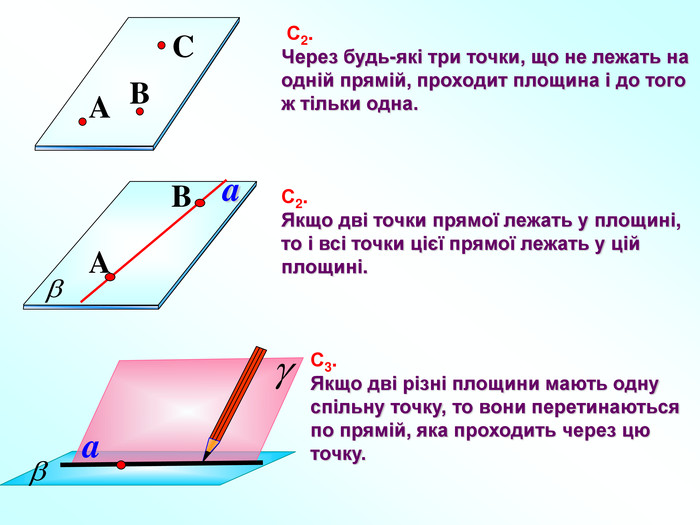
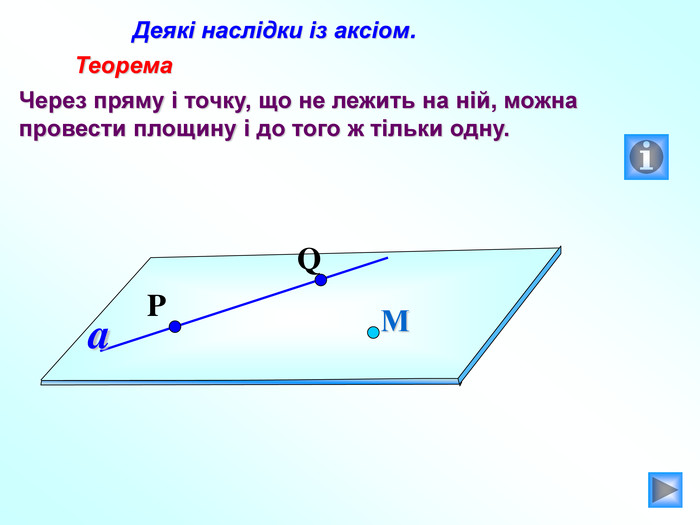
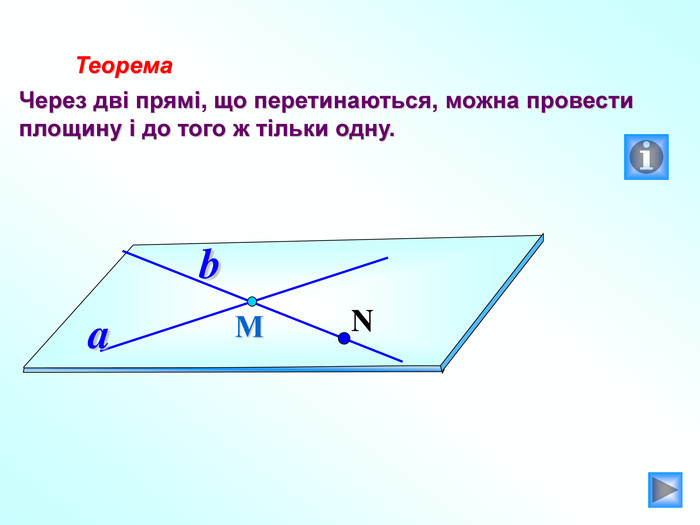
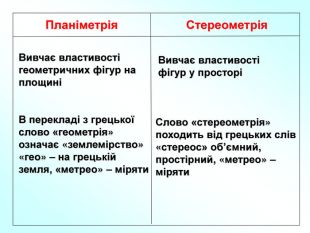
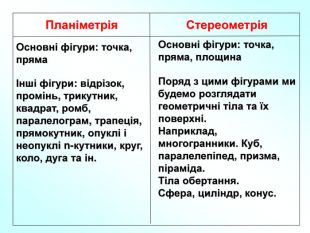
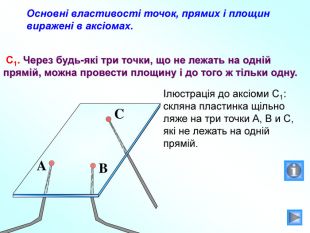
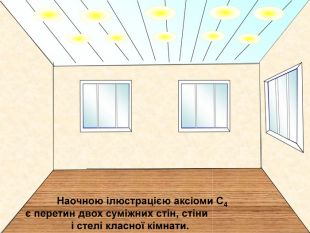
Презентація до уроку "Вступ до стереометрії" містить наочні приклади основних аксіом та теорем стереометрії, також порівняння спільного матеріалу з планіметрією, практичне застосування аксіом стереометрії в архітектурі і техніці
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку



















-

Новомлинська Дар'я Сергіївна
10.11.2020 в 21:30
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Курган Тетяна Володимирівна
10.11.2020 в 19:28
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Нижник Тетяна Юріївна
30.08.2020 в 13:22
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

В В
04.12.2019 в 23:36
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 1 відгук