Презентація до уроку "Метричні співвідношення в трикутнику та чотирикутнику"
Презентація створена до уроку-семінару.
Урок-семінар
Тема:Метричні співвідношення в трикутнику та чотирикутнику
Мета: Поглибити знання учнів з математики, навчати дослідницькій діяльності; розвивати пізнавальний інтерес, виховувати повагу до науки.











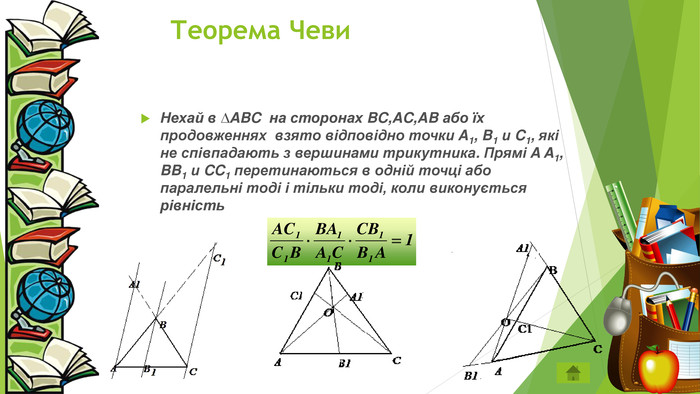
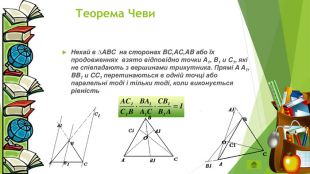
![Джованні Чева. Джованні Чева (італ. Giovanni Ceva; 7 грудня 1647 - 15 червня 1734 [1]) - італійський математик і інженер, що довів теорему Чеви про геометрію трикутника. Основною заслугою є побудова вчення про січні, яке поклало початок нової синтетичної геометрії. Воно викладено в творі «Про взаимопересекающихся прямих» (De lineis rectis se invicem secantibus, statica constructio, 1678). [2]Джованні Чева здобув освіту в єзуїтському коледжі Мілана, а в 1670 році поступив в Пізанський університет. У 1685 році одружився на Сесілії Веччі, у них було кілька дітей. Чева був інженером-гідравліки і як такий кілька разів служив уряду Мантуї. Смерть його послідувала під час облоги Мантуї. Також він опублікував одну з перших робіт по математичній економіці (De re nummeraria, 1 711), в якій розглядалися умови рівноваги грошової системи Мантуї. Джованні Чева. Джованні Чева (італ. Giovanni Ceva; 7 грудня 1647 - 15 червня 1734 [1]) - італійський математик і інженер, що довів теорему Чеви про геометрію трикутника. Основною заслугою є побудова вчення про січні, яке поклало початок нової синтетичної геометрії. Воно викладено в творі «Про взаимопересекающихся прямих» (De lineis rectis se invicem secantibus, statica constructio, 1678). [2]Джованні Чева здобув освіту в єзуїтському коледжі Мілана, а в 1670 році поступив в Пізанський університет. У 1685 році одружився на Сесілії Веччі, у них було кілька дітей. Чева був інженером-гідравліки і як такий кілька разів служив уряду Мантуї. Смерть його послідувала під час облоги Мантуї. Також він опублікував одну з перших робіт по математичній економіці (De re nummeraria, 1 711), в якій розглядалися умови рівноваги грошової системи Мантуї.](/uploads/files/55861/31696/31547_images/18.jpg)
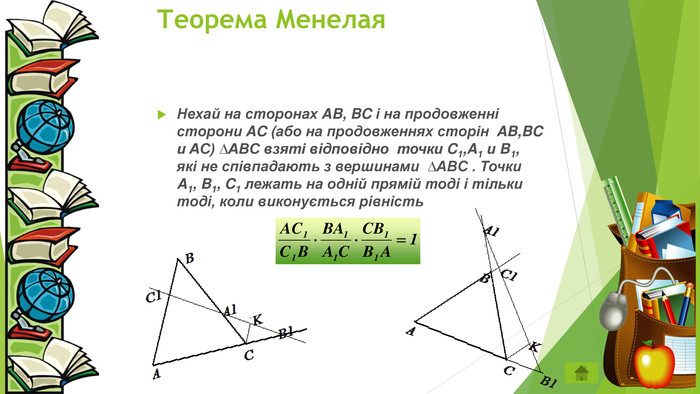




Вклад вчених в розвиток тригонометріїУ IX – XV ст. на розвиток тригонометрії великий вплив зробили народи, що населяли територію теперішніх середньоазіатських країн, країн Закавказзя, Іраку, Афганістану і Сирії. Аль – Хорезмі (IX ст.) систематизував індійські таблиці тригонометричних величин. Абуль – Вефа (940 – 998рр) склав таблиці синусів через кожні 10 мінут. Вінцем досягнень середньоазіатських вчених у галузі тригонометрії можна вважати відділення її від астрономії і виокремлення в самостійну науку. Головна заслуга в цьому належить азербайджанському вченому Насиреддіну Тусі (1201 – 1274рр). У його праці ми вперше зустрічаємо доведення теореми синусів і теореми тангенсів. У складанні тригонометричних таблиць видатних успіхів досяг узбецький вчений з м. Самарканда Аль – Каші (помер близько 1430р.). Він обчислив таблиці синусів з точністю до однієї мільярдної. Це були найточніші таблиці на той час. Німецький математик Йоган Мюллер (1436 – 1476) першим з європейських учених дав послідовний виклад тригонометрії , обчислив дуже точні таблиці синусів і тангенсів. Багато для розвитку тригонометрії зробили й інші вчені. Завдяки праці кількох поколінь учених тригонометрія стала самостійною наукою.
1. Задачі на знаходження висоти предмета, основа якого недоступна. Задача. Знайдіть висоту вежі, яка відокремлена від вас річкою. Розв’язання. На горизонтальній прямій, яка проходить через основувежі, позначимо дві точки А1 і С1. Вимірюємо А1 С1= b, DAB = α і DCB = β. За теоремою синусів, з трикутника АВС дістанемо: АВ=АС∙𝑠𝑖𝑛𝛽𝑠𝑖𝑛𝐵. З прямокутного трикутника ABD: BD = AB · sin α. Отже, 𝐵𝐷=𝑏∙𝑠𝑖𝑛𝛼∙𝑠𝑖𝑛𝛽sin(𝛼−𝛽)Додавши до BD висоту приладу 𝐴𝐴1=DK= h, яким вимірювали кути, дістанемо формулу для обчислення висоти вежі: ВK = ВD + DK =𝑏∙𝑠𝑖𝑛𝛼∙𝑠𝑖𝑛𝛽sin(𝛼−𝛽)+h.
2. Задачі на знаходження відстані до недоступного пункту. Задача. Знайдіть відстань від пункту А до недоступного пункту В. Розв’язання. Обираємо на місцевості таку точку С, щоб з неї було видно пункт В і можна було виміряти відстань АС. Вимірюємо АС = b, ВАС = α, ВСА = γ. Знаходимо В = 180° – α – γ. За теоремою синусів: Нехай результати вимірювання такі: b = 90 м, α = 46°, γ = 25°. Тоді
3. Задачі на знаходження відстані між двома доступними пунктами(якщо безпосереднє вимірювання неможливе). Задача. Знайдіть відстань між пунктами В і С, розділеними ставком. Розв’язання. Обираємо на місцевості точку А так, щоб можна було виміряти відстані АВ і АС. Вимірюємо АВ = с, АС = b і ВАС = α. За теоремою косинусів: Нехай результати вимірювання такі: b = 88 м, с = 90 м, α = 28°. Тоді
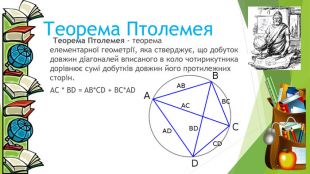
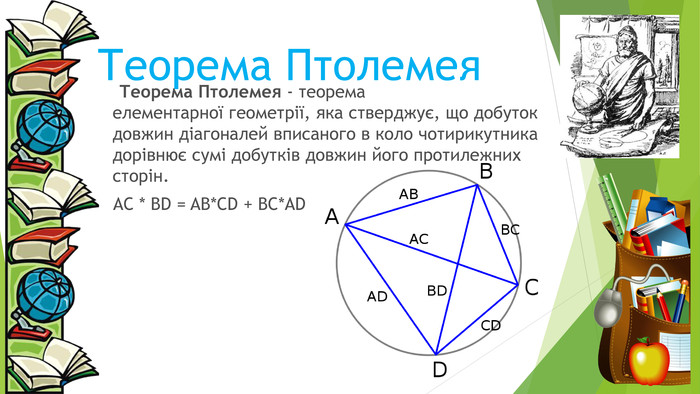
Клавдій Птолемей (близько 87 — 165) —давньогрецький вчений,твори якого мали великий вплив на розвиток астрономії, географії та оптики. Дані про життя Птолемея мізерні. Жив у римській провінції Єгипет і працював в Александрії. Створив геоцентричну систему світу, розробив математичну теорію руху планет навколо нерухомої Землі, яка дозволяла обчислювати їхнє положення на небі. Система Птолемея викладена в його головній праці «Альмагест» — енциклопедії астрономічних знань давнини. У 1543 польський астроном Микола Копернік запропонував альтернативну, геліоцентричну систему. У праці Птолемея «Географія» були представлені географічні відомості античного світу, нею користувалися аж до 16 століття.
Джованні Чева. Джованні Чева (італ. Giovanni Ceva; 7 грудня 1647 - 15 червня 1734 [1]) - італійський математик і інженер, що довів теорему Чеви про геометрію трикутника. Основною заслугою є побудова вчення про січні, яке поклало початок нової синтетичної геометрії. Воно викладено в творі «Про взаимопересекающихся прямих» (De lineis rectis se invicem secantibus, statica constructio, 1678). [2]Джованні Чева здобув освіту в єзуїтському коледжі Мілана, а в 1670 році поступив в Пізанський університет. У 1685 році одружився на Сесілії Веччі, у них було кілька дітей. Чева був інженером-гідравліки і як такий кілька разів служив уряду Мантуї. Смерть його послідувала під час облоги Мантуї. Також він опублікував одну з перших робіт по математичній економіці (De re nummeraria, 1 711), в якій розглядалися умови рівноваги грошової системи Мантуї.
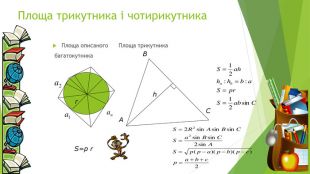
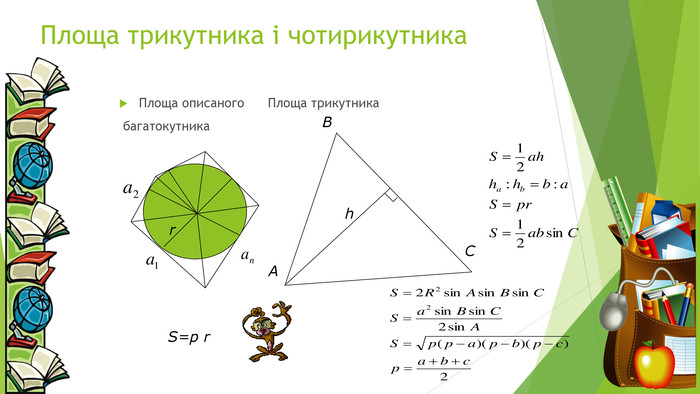
Теорема Брахмагупта. Дано довільний 4-кутник навколо якого можно описати коло. Нехай довжини його сторін a, b, c, d. Тоді площайого буде обчислюватись за формулою. S=(p-a) (p-b) (p-c) (p-d)Якщо чотирикутник такий, що в нього можно і вписати і описaти навколо нього коло, то його площад может бути обчислена за формулою S=a b c d


про публікацію авторської розробки
Додати розробку