Урок "Поняття вектора у просторі. Операції над векторами"

Тема: КООРДИНАТИ І ВЕКТОРИ

СТРУКТУРА УРОКУ

Урок № 4

Тема уроку:   Поняття вектора у просторі. Операції над векторами 

Мета уроку:

• сформулювати поняття вектора в просторі та пов’язані з ним поняття абсолютної площини, напряму, рівності векторів, види векторів;
• навчити оперувати діями над векторами;
• розвивати просторову уяву, пам'ять, уміння проводити аналогії;
• виховувати наполегливість, працьовитість;
• проявляти ініціативність, відповідальність, упевненість у собі.

Тип уроку. Засвоєння нових знань і вмінь

Наочність та обладнання: презентація «Вектори на площині» ( підготовлена дитиною високого рівня навчання); картки-заготовки для с/р.

Очікувані результати.

Учень/учениця: користується аналогією між векторами на площині й у просторі;

Після закінчення уроку учень/учениця:

• знає: що таке вектор, як зображують  та позначають вектор, розрізняє спів-напрямлені та протилежно напрямлені вектори, рівні вектори, колінеарні та компланарні вектори
• вміє: побудувати вектор, суму векторів за правилом трикутника та правилом паралелограма, правилом трапеції
• може: сформулювати задачу на мові векторів, перетворювати векторні рівності.

 

Хід уроку

 

І. Організаційний момент.

Епіграф нашого уроку:

Ваша сила - віра в себе.

Самостійні думки виникають тільки

із самостійно  отриманих знань.

 К.Ушинський

ІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ

 Учні-консультанти доповідають вчителеві про готовність класу до уроку та наявність виконання домашнього завдання учнями. Вчитель відповідає на запитання учнів, які виникли під час виконання домашнього завдання.

ІІІ. ФОРМУЛЮВАННЯ ТЕМИ, МЕТИ І ЗАВДАНЬ УРОКУ

 Розповідь про місце уроку в системі уроків теми, вивчення якої розпочинається. Розповідь про місце уроку в системі уроків теми, вивчення якої розпочинається.                      Поняття вектора є важливим у математиці та фізиці. Існує чимало важливих величин, котрі є векторами. Наприклад, сила, швидкість, прискорення, кутовий момент, напруженість електричного і магнітного полів. Ці величини можна протиставити іншим величинам, таким як маса, об’єм, тиск, температура та густина, які можна описати звичайним числом, їх називають скалярами. Тому знання про вектори є важливими при вивченні природничо-математичних наук.

        Сьогодні на уроці ми повторимо  знання  про вектори в просторі, розглянемо задачі , що передбачають використання  властивостей додавання та віднімання векторів (графічно). Оскільки тему «Вектори» ви вже вивчали в курсі геометрії 9-го класу. Спробуємо пригадати відомі нам факти і провести паралель між теорією  вектор на площині і вектор в просторі.

ІV. Актуалізація опорних знань і вмінь учнів проходить в співпраці вчителя і учнів, де в більшості говорять учні, а вчитель лише їх направляє .

V. ЗАСВОЄННЯ ЗНАНЬ

ПОЯСНЕННЯ НОВОГО МАТЕРІАЛУ ( учні працюють з підручником і дають відповіді на запитання вчителя)

1. Що ми називаємо  вектором  та його позначення ?

 

 

 

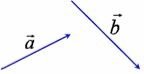
 Щоб зрозуміти різницю між відрізком і вектором звернемось до прикладу: уявіть собі, що ви маєте стрілу і звичайну рівну палицю однакової довжини і товщини. Знайдіть різницю між палицею і стрілою. Якщо Ви  уважні, то побачите, що стріла, на відміну від відрізка має напрям. Тобто ми завжди з певністю можемо визначити де в стріли початок, а де кінець, що є суттєвим.

2. Що ми розуміємо під довжиною вектора, як її позначають?
3. Коли два вектори будуть рівні?
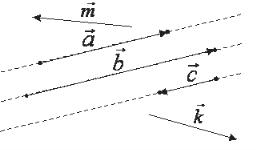4. Які вектори називаються колінеарними? За рисунком назвіть їх.

 

 

 

 

 

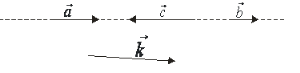5. Що собою являють однаково напрямлені і протилежно напрямлені вектори?

 

 

6. Розтлумачити записи:

                  ,   

 Багато фізичних величин повністю визначаються лише своїм числовим значенням (об’єм, густина, маса) – такі величини називаються скалярними. Але є й такі величини, які крім числового значення мають характеризуються ще й напрямом (швидкість, сила, напруженість) – такі величини називають векторними.

Дії  над векторами

1.  Множення вектора на скаляр

 Нехай задані вектор  і число . Добутком називається вектор, довжина якого дорівнює , а напрям збігається з напрямом, якщо >0 і протилежний , якщо <0.

2.  Додавання векторів

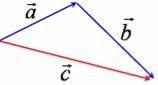
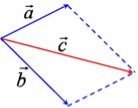
Правило трикутника	Правило паралелограма
Сумою (+) двох векторів  і  є такий вектор , напрямлений з початку вектора  в кінець вектора  за умови, що початок вектора  збігається з кінцем вектора .	Сумою (+) двох векторів  і  є такий вектор , напрямлений з початку векторів  і  вздовж діагоналі паралелограма, сторони якого утворені з векторів  і  їх паралельним переносом за умови, що початки векторів  та  збігаються.

 

СПРИЙМАННЯ І УСВІДОМЛЕННЯ НОВОГО МАТЕРІАЛУ

VІ. Осмислення і усвідомлення вивченого матеріалу

1) Усно з коментуванням з місця: №№ 3.50; 3.51; 3.53; 3.60;

2) Два учня працюють за закритою дошкою,  клас в цей час самостійно:

№  3.58 та № 3.64

VII.  Відпрацювання вмінь та навичок

Задача 1.                                                       

1.  
2.  
3.  
4.  

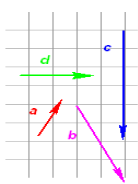  Задача 2.

 

 

 

 

 

Побудувати:1)  а-b; b-d; d-b (за правилом трикутника – три учня біля дошки)

                      2) )  а-b; b-d; d-b (за правилом  паралелограма – три учня біля дошки)

VIII. Удосконалення вмінь і навичок

Самостійна робота

Дано вектори а і b (дивись малюнок). Побудувати вектори а + b, a – b, a, –2b

 

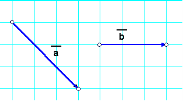Варіант І

 

 

 

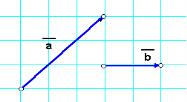Варіант ІІ

 

 

 

 

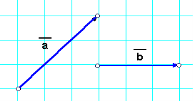Варіант ІІІ

 

 

 

 

 

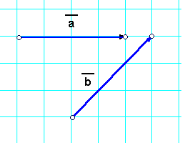Варіант IV

 

 

 

 

 

 

ІХ. Домашнє завдання:

Опрацювати §3.3 (ст.. 16-23)

Повторити: дії з векторами  на площині

Виконати:3.52; 3.56; 3.62

     Додаткова задача

ABCD — паралелограм. Які векторні рівності можна записати?

Х. Підсумки уроку. Оцінювання:

Підсумок уроку за схемою:

1. Важливо знати :
2. Важливо уміти:
3. Зауважте:

 Під час цілого уроку належно працювали:…

Особливої похвали заслуговують такі учні: …

Оцінювання (не менше 3-ох оцінок)

XI. Рефлексія (осмислення результатів уроку)

      Світлофор:

 

• Багато незрозумілого
• Є питання
• Все зрозуміло

 

 

Тема: КООРДИНАТИ І ВЕКТОРИ

 

 

СТРУКТУРА УРОКУ

Урок № 5

Тема уроку: Розв’язування задач.

Мета уроку:

• систематично стежити за грамотністю висловлювання учнів рідною мовою, доречним та коректним вживанням у мовленні математичної термінології;
• розв’язувати задачі, застосовуючи теоретичні знання;   
• домогтися засвоєння властивостей дій над векторами;
• дати можливість кожній дитині проявити  ініціативність, відповідальність, упевненість у собі;

Тип уроку. Застосування знань і вмінь

Наочність та обладнання:картки для гри «Математичне доміно»

Очікувані результати.

Учень/учениця: виконує операції над векторами.

Після закінчення уроку учень/учениця:

• знає: розв’язувати задачі на побудову суми та різниці векторів;
• вміє: вміє побудувати вектор, що дорівнює скалярному добутку числа та даного вектора;
• може: розрізняти співнапрямлені вектори та протилежно напрямлені вектори.

 

Хід уроку

І. Організаційний момент.

От і все дзвенить дзвінок,

Вгості йде до нас урок!

Добрий день!

Сідайте зручно!

Я бажаю вам удачі!

Розв’яжіть усі задачі,

Що постануть перед вами

На уроці нашім славнім!

                          ---  налаштування на роботу

Епіграф нашого уроку:

Мистецтво вирішувати геометричні задачі

чимось нагадує трюки ілюзіоністів

 – іноді, навіть знаючи рішення задачі,

важко зрозуміти, як можна було до нього додуматися.

Стефан Банах, польський та український математик.

ІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ

 

Математичний  диктант  Варіант  1 1.Запишіть  коротко  «вектор  а». 2. Зобразити  вектор  . 3.Запишіть  позначення  вектора  з  кінцем  у  точці  Х  та  початком  у  точці  У. 4.Зобразити  два  однаково  спрямованих,  але  не  рівних  вектора. 5.Що  можна  сказати  про  напрямок  двох  рівних  векторів ? 6.Запишіть  у  вигляді  рівності,  чому  дорівнює  абсолютна  величина  нульового  вектора. 7. Зобразити вектор    і  точку  У.  Відкладіть від  точки  У  вектор,  рівний  . 8. Запишіть  за  допомогою  позначень  «довжина  вектора    дорівнює  3 см». 9.Знайдіть  довжину  вектора,  зображеного  на  рисунку:                                      Т                                            3 см             S                                     5 см                            10.  Чи вірно  твердження:  «Якщо  вектори    й    рівні,  то  вони  колінеарні»?

Математичний  диктант   Варіант  2 1.Запишіть  коротко  «вектор  в». 2. Зобразити вектор  . 3.Запишіть  позначення  вектора  з  кінцем  у  точці  Р  та початком  у  точці  А. 4.Запишіть  у  вигляді  рівності,  чому  дорівнює  абсолютна  величина  нульового  вектора. 5. Зобразити  вектор    і  точку  М.  Відкладіть  від  точки  М  вектор,  який дорівнює  вектору  . 6.Що  можна  сказати  про  напрямок  двох  рівних  векторів ? 7.Зобразити  два  однаково  спрямованих,   але  не  рівних  вектора. 8. Запишіть  за  допомогою  позначень  «довжина  вектора    дорівнює  4 см». 9.Знайдіть  довжину  вектора,  зображеного  на  малюнку:                                        М          К                                    2 см                             6 см 10. Чи вірно  твердження:  «Якщо  два  вектори  колінеарні,  то  вони  однаково спрямовані»?

 

ІІІ. ФОРМУЛЮВАННЯ ТЕМИ, МЕТИ І ЗАВДАНЬ УРОКУ

Сьогодні на уроці ми з вами будемо розв’язувати задачі, пов’язані з векторами.

ІV. Актуалізація опорних знань .

Гра «Математичне доміно»

( Учитель готує набір карток двох кольорів. На одних записується початок речення, на інших його закінчення ;  діти працюють в парах ).

Початок речення	Закінчення речення
Вектори називаються рівними …	Якщо вони співнапрямлені і мають рівні довжини
Два ненульових вектори називаються колінеарними…..	Якщо вони паралельні одній прямій
Щоб задати вектор…	Достатньо вказати його початок і кінець.
Два вектори називають протилежними векторами….	Якщо вони мають рівні модулі, але протилежні напрями.
Співнапрямленими векторами називають колінеарні вектори…	Якщо вони мають однаковий напрямок.
Нуль-вектором називають вектор…	Якщо його початок і кінець співпадають.
Довжиною вектора називають…	Відстань між його початком і кінцем.
Довжина нуль-вектора….	Дорівнює нулю.
Довжина і напрям вектора не залежать від…	Розміщення його початку в системі координат
Вектори рівні…	Коли їх відповідні координати рівні.
Вектори колінеарні…	Коли їх відповідні координати пропорційні

 

(Кожній  парі  учнів роздається доміно, яке необхідно скласти у відповідності:  початок речення – кінець )

V. Осмислення і усвідомлення вивченого матеріалу

1) Біля дошки : № 3.66; 3.68( робота з підручником) ,  ( два учня біля дошки, клас – с/о)

2)Задача 1( усно).  Користуючись рисунком,  назвіть вектори, що є:

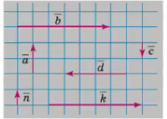1) колінеарними;

2) спів напрямленими;

3) протилежно напрямленими;

4) рівними;

5) протилежними?

 VI. Удосконалення вмінь і навичок

Задача 2(письмово)

На сторонах АВ і ВС паралелограма АВСД  позначено відповідно точки М і N  так, що АМ:МВ=1:2,  BN:NC=2:1. Виразіть вектор NM через вектори АВ  = a,    АД = b    .

Задача 3(письмово)

Дано паралелепіпед ABCDA₁В₁С₁D₁. Розкласти за векторами AB =   a ,   AD  =  b ,    AA  =  =  c    вектори: 1) C₁A; 2) AC ; 3) DC₁ .

VI.  Домашнє завдання:

повторити§3.3

виконати №№ 3.70; 3.72

VІI. Підсумки уроку. Оцінювання.

VIІI. Рефлексія (осмислення результатів уроку)

      Рефлексія діяльності на уроці

«Плід» - урок пройшов корисно, плітно

«Квітка» - досить непогано

«Зелений листочок» - щось було,  звичайно, але взагалі – не зрозуміло

«Жовтий листочок»-  «чахлий», невдалий урок