Посібник для уроків курсу за вибором "Математичні смарагди" 6 класу І семестр

Про матеріал

Посібник містить розробки занять для курсу за вибором у 6 класі "Математичні смарагди"

Перегляд файлу

Любі учні!

Сучасний світ неможливо уявити без математики. Саме вона є царицею всіх наук. Без обчислень, розв’язування задач, прикладів важко жити в сучасному світі.

Посібник, який ви тримаєте в руках, допоможе вам засвоїти знання, розвинути вміння з математики. Він спрямований на вивчення курсу «Математичні смарагди» у 6 класі.

Будьте уважними, активними і наполегливими, не лінуйтеся і таким чином принесете радість собі, своїм батькам і Творцю.

Нехай Бог посилає мудрості у вивченні математики!!!

Тема №1. Геометричні головоломки

Уроки №1, 2

«Природа говорить мовою математики:

букви цієї мови — круги, трикутники та

інші математичні фігури».

Г.Галілей

Задачі з сірниками

Мета: формувати евристичне мислення у дітей; здатність до аналізу та синтезу, узагальнення і конкретизації, абстрагування, вміння виділяти суттєве, розвивати і активізувати логічне мислення, розвивати увагу, пам'ять, виховувати розвитку почуття колективізму, взаємодопомоги.

Хід уроку

1 Організаційна частина

2 Відгадування загадки

Дерев’яні хлопці

Лежать у коробці.

Коли з ними граються,

То вогнем займаються. ( сірники)

Вступна бесіда про сірники

---- Що ви знаєте про сірники?

Сірник — дерев'яна паличка для створення вогню за потреби. Сірники зазвичай виготовляються з деревини або іноді з цупкого паперу, картону. Дерев'яні сірники продаються в коробках, а паперові сірники — в пакетиках або книжечках. На одному кінці сірник має голівку, вкриту запалювальною речовиною, яка називається сірка, тому так і називаються сірники. Сірники дуже необхідна річ в побуті.

— А коли виникли сірники?

Раніше, до винаходу сірників, одержати вогонь було дуже складним завданням. Люди терли одна об одну палички, ловили склом сонячні зайчики, вибивали іскру з каменів і чого тільки не придумували для того, щоб одержати вогонь. А потім вчені люди винайшли так звані «сірники-маканки». Це такі палички, на які наносилася сіль, і запалювалися вони після того, коли їх занурювали у спеціальний розчин Але дуже не зручно було кожного разу цей розчин носити з собою. І от одному вченому спала на думку ідея нанесення на палички такої суміші, що легко запалювалася при терті об наждаковий папір. Ці сірники одержали назву «сухі сірники». Але вони дуже сильно смерділи, були дуже дорогими. І тому з'явилися нові сірники, які легко запалювалися об запалювальну смужку і були абсолютно безпечні для здоров'я. А потім уже придумали і сірникову коробочку. Смужка «запалювання» була на бортику коробки. Раніше вона перебувала всередині. 178 років тому виникли сірники.

---- Діти ви чули коли- небудь такі слова «Сірники дітям не іграшка, а зарядка для розуму». В наш час сірники використовують не тільки для розпалювання вогню, а ще творчі люди виготовляють з них скульптури, картини. Якщо сірники не запалювати, а ще краще замінити їх на тоненькі палички( зубочистки) , то можна придумати багато різних математичних розваг. Я вам розкрию один секрет. В звичайнісінькій сірниковій коробці живуть головоломки? Звичайно, вони не живуть там тоді, коли ми використовуємо сірники для запалювання вогню. Але вони одразу поселяються у сірниковій коробці тоді, коли сірники перестають бути звичайними сірниками, а перетворюються на цифри, слова чи фігури. Сьогодні сірники будуть деталями «сірникових» задач. Hе вірите? Тоді спробуємо розв’язати математичні головоломки і ми побачимо, що без кмітливості та математичних знань ми не можемо розгадати головоломки.

Оголошення теми і мети уроку

---- Отже тема нашого уроку «Задачі з сірниками». Сьогодні на уроці ми з вами будемо тренувати мислення, увагу, кмітливість. Але пам’ятаємо, що нам необхідні будуть знання з математики, з української мови.

Завдання 1.

Складіть своє ім’я.
Переставивши лише один сірник, із чоловічого імені ТОЛЯ утвори жіноче ім’я. ( ЮЛЯ)

Завдання 2.

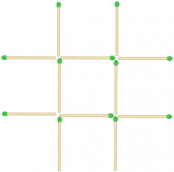
Дванадцять сірників лежать так, як показано на малюнку. Скільки тут квадратів?
Виконаєте наступні завдання:
1) заберіть 2 сірника так, щоб утворювалося 2 нерівних квадрата;
2) перекладете 3 сірника так, щоб утворювалося 3 рівних квадрата;
3) перекладете 4 сірника так, щоб утворювалося 10 квадратів.

ÐÐ²Ð°Ð´ÑÐ°Ñ ÑÐ· 12 ÑÑÑÐ½Ð¸ÐºÑÐ²

Відповідь на перше завдання:

Квадрат із 12 сірників - Відповідь на перше завдання

Відповідь на друге завдання:

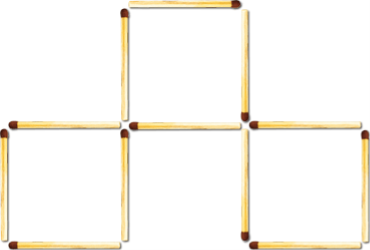
Квадрат із 12 сірників - Відповідь на друге завдання

Відповідь на третє завдання:

Квадрат із 12 сірників - Відповідь на третє завдання

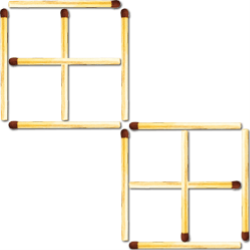
Завдання 3.

Перекладіть 3 сірника так, щоб стріла поміняла свій напрямок на протилежний.

Стрілка

Відповідь.

Стрілка - Відповідь

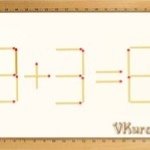
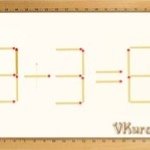
Із сірників склали приклад римськими цифрами. Тільки от вийшло, що 6 - 4 = 9...
Пересуньте 1 сірник так, щоб рівність стала правильною.

Римські цифри 1

Відповідь. 6 + 4 = 10.

Римські цифри 1 - Відповідь

Всередині квадратного озера розташований квадратний острів (див. малюнок). Це все ми виклали із сірників. Потрібно спорудити надійну переправу із зачепами із двох сірників, що залишилися.

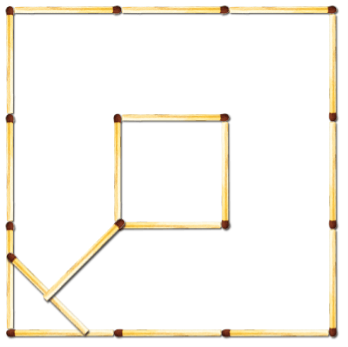
Переправа на острів

Відповідь

Переправа на острів - Відповідь

Є 13 сірників по 5 см довжиною кожен. Потрібно зуміти викласти з них метр.

Відповідь

«Метр» - Відповідь

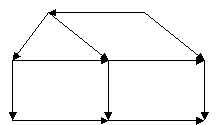
Перекладіть сірники так, щоб будиночок повернувся іншим боком.

Відповідь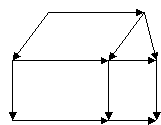

Завдання 4 (самостійна робота по групах)

Група 1.

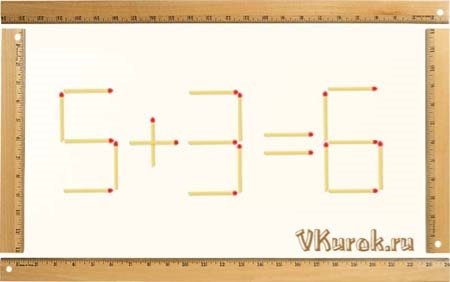
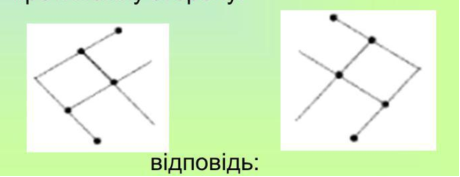
На малюнку з сірників викладена невірна рівність 5+3=6. Перекладіть 1 сірник так, щоб рівність стала вірною. (Можливі 2 варіанти рішення).

Завдання з математики

Переставте три сірники так, щоб рибка попливла в зворотному напрямку.

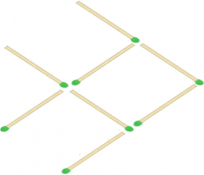
Відповідь:

Група 2.

На картинці з сірників викладена невірна рівність 36+4=108. Перекладіть 1 сірник, щоб рівність стала вірною.

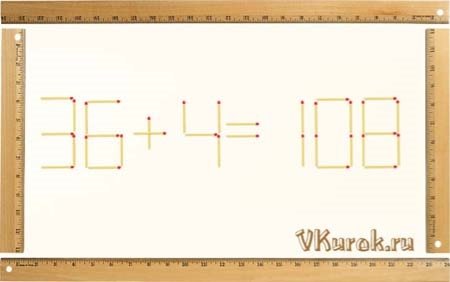
Завдання з математики

Відповідь:

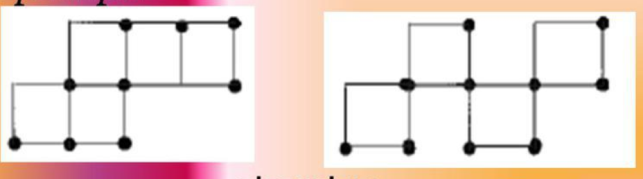
Маючи 16 сірників, перекладіть 2 сірника так, щоб з п’яти квадратів отримати 4 квадрати таких же розмірів.

Група 3.

На малюнку з сірників викладена невірна рівність 4*11=411. Перекладіть 1 сірник, щоб рівність стала вірною.

Завдання з математики

Відповідь:

2. Необхідно перекласти 3 сірники так, щоб отримати рівно 3 квадрата.

Уроки № 3, 4

На базарі їх не купиш, на дорозі не знайдеш,

їх не зважують на терезах і ціни не підбереш. Що це?

Головоломки з паперу у клітинку

1. Які з наведених многокутників мають однакові периметри?

Малюнок 1

А Б

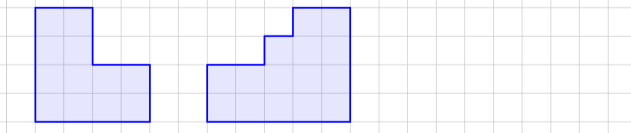
В Г

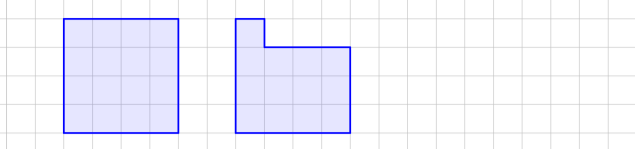
Малюнок 2

А Б

фігури

В Г

фігури

2. Які з наведених многокутників мають однакові площі?

Рисунок 1

А Б

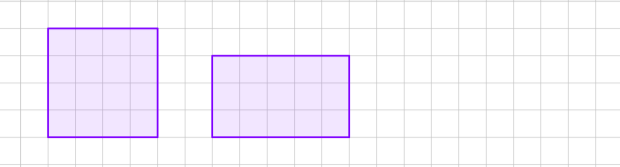
В Г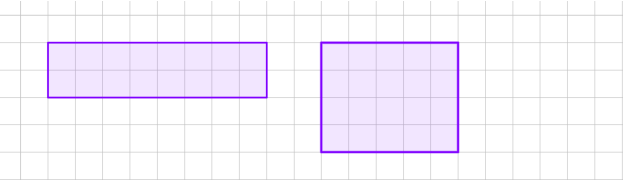

Рисунок 2

А Б

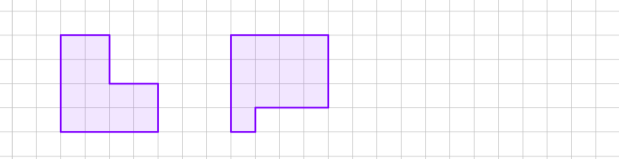
В Г

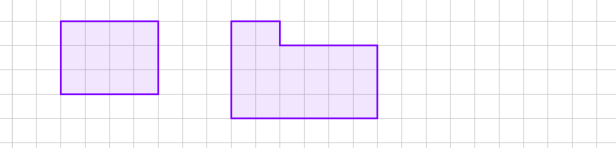
3. Скільки квадратів можна знайти на цих малюнках?

А Б

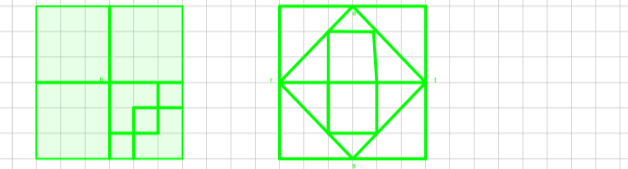
4. У скільки разів площа зафарбованого квадрата менша від загальної площі прямокутника ( довжина 1 клітинки становить 1 см) ?

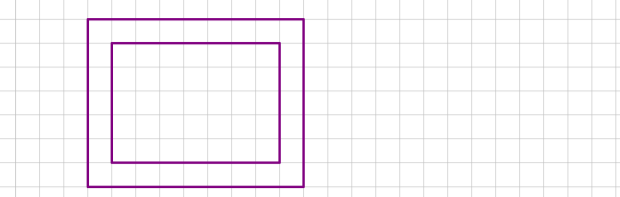
5. Знайди площу рамки ( довжина 1 клітинки становить 1 см).

6. Скільки квадратів зі стороною 2 см потрібно, щоб покрити даний прямокутник

( довжина 1 клітинки становить 1 см)?

Рисунок 1

А.3 Б. 4 В. 5 Г. 6

Рисунок 2

А. 5 Б.3 В.4 Г.6

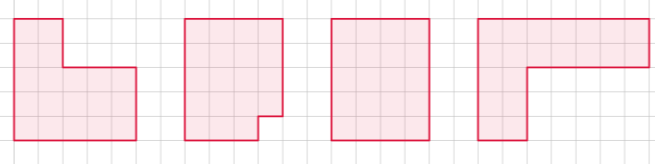
7. Які з наведених фігур мають однакові периметри, але різні площі ( довжина 1 клітинки становить 1 см)?

А Б В Г

8. На фарбування 1 м ²підлоги витрачається 250 г фарби. Чи вистачить 4 банки фарби по 3 кг в кожній, щоб пофарбувати підлогу в класній кімнаті довжиною 8 м і шириною 6 м?

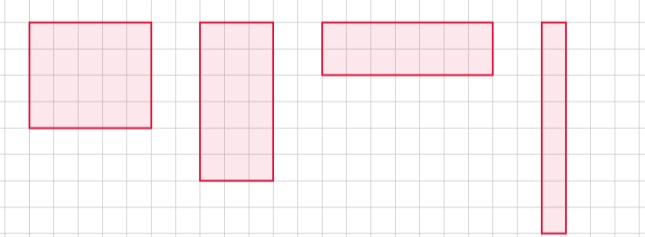
9. Знайти периметри даних прямокутників. Порівняйте їх. Знайти їх площі ( довжина 1 клітинки становить 1 см).

10. Визнач площу квадрата. Накресли прямокутники, які мають таку ж площу ( довжина 1 клітинки становить 1 см).

Відповідь:

1. Рис. 1 ( А, В, Г); рис. 2 (Б, Г)

2. Рис. 1 ( А, В, ); рис. 2 (А, В)

3. А-8; Б-4

4. У 3 рази

5. 28 см²

6. Рис. 1 (Б); рис. 2 (В); рис. 3 (Г)

7. Б; В

8. Вистачить

Площа (S)	Периметр (Р)
18 см²	20 см
18 см²	18 см
18 см²	14 см
18 см²	8 см

Урок № 5

Арифметичні узори

Завдання 1.

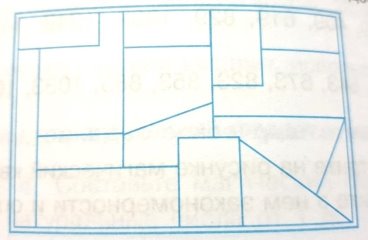
Графічна задача. Розмалюйте фігури в коробці в різні кольори так, щоб фігури однакового кольору не мали спільних кордонів. Використовуйте мінімальну кількість кольорів. Скільки різних кольорів вам знадобилось?

$C:\Users\алло\Desktop\20200630_103611.jpg$

Завдання 2.

Арифметичні килимки

Різновид арифметичних головоломок у вигляді прямокутників, в які необхідно розставити числа, яких не вистачає так, щоб всі рівності, розміщені по вертикалі і горизонталі, були правильними.

Впишіть у порожні клітинки квадрата одноцифрові числа так, щоб всі рівності були правильними.

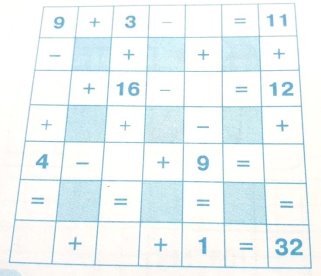
$C:\Users\алло\Desktop\20200630_104419.jpg$

Заповніть порожні клітинки так, щоб всі рівності в арифметичному килимку були правильними.

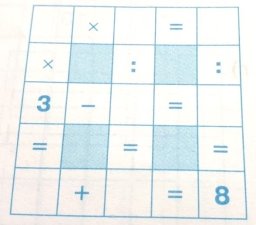
$C:\Users\алло\Desktop\20200630_104412.jpg$

Заповніть арифметичний килимок, вставляючи числа і знаки арифметичних дій так, щоб всі рівності були вірними.

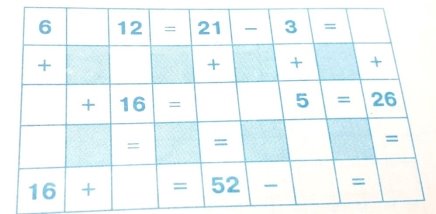
$C:\Users\алло\Desktop\20200630_104426.jpg$

Завдання 3.

Арифметичні візерунки

Вид арифметичних головоломок, схожих на візерунки із квадратиків і кружечків, які потрібно заповнювати числами так, щоб виконувались певні умови.

3.1. Кожну зафарбовану комірку оточіть числами від 1 до 6 так, щоб ніякі дві комірки з однаковими числами не мали спільних кордонів.

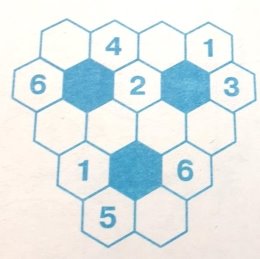
$C:\Users\алло\Desktop\20200630_105305.jpg$

3.2. Впишіть в клітинки візерунку числа від 1 до 9 так, щоб виконувались отримані арифметичні нерівності (числа в арифметичному візерунку не повторюються).

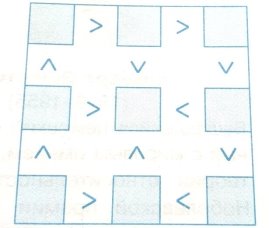
$C:\Users\алло\Desktop\20200630_105313.jpg$

3.3. Розташуйте в кружечках числа від 1 до 8 так, щоб ні в одному із двох сполучених кружечків не було числа, яке відрізняється на 1.

Підказка. 1. Кожне число, крім 1 і 8, має по два числа сусіда, значить, тільки п’ять чисел можуть бути сполучені з числами 2, 3, 4, 5, 6, 7.

2. В двох центральних кружечках, які з’єднані з шістьма іншими можуть бути розміщені лише числа 1 і 8.

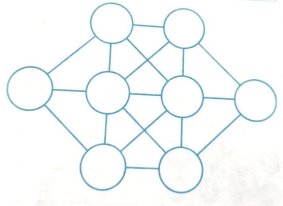
$C:\Users\алло\Desktop\20200630_105320.jpg$

Домашнє завдання. Заповніть порожні клітинки так, щоб всі рівності в арифметичному килимку були правильними.

$C:\Users\алло\Desktop\20200630_105438.jpg$

Тема №2. Текстові задачі

Уроки №1, 2

Деякі задачі на принцип Діріхле

Німецький математик Петер Лежен Діріхле у своїх наукових працях часто користувався міркуваннями, які зараз називають принципом Діріхле.

Знайомство із цим принципом можна розпочати із задачі: «Чи можна розмістити 5 кроликів у чотирьох клітках так, щоб у жодній з кліток не містилося більше одного кролика?»

Розв’язати задачу можна завдяки таким міркуванням: якби у кожній клітці сиділо не більше одного кролика, то у чотирьох клітках помістилося б не більше чотирьох кроликів. А тому п’ять кроликів таким способом не можна розмістити.

Задача 1. У похід пішли 12 туристів. Наймолодшому з них – 20 років, а найстаршому – 30. Чи є серед них однолітки?

Розв’язання

Туристи утворюють 30–20+1=11 вікових груп.

Тому є 11 груп (кліток) і 12 туристів (кроликів). Оскільки 12>11, то принаймні в одній віковій групі знайдеться два туристи, які є однолітками.

Задача 2. На 5 поличках розміщено 160 книг, причому на одній із них - 3 книги.

Доведіть, що знайдеться поличка, на якій буде стояти не менше ніж 40 книг.

Розв’язання

Нехай на кожній із решти 4 поличок не більше ніж 39 книг. Тоді на всіх 5 поличках не більше ніж 3 + 4∙39 = 159 книг, що суперечить умові. Отже, на одній із поличок не менше ніж 40 книг.

Задача 3. У школі навчається 400 учнів. Доведіть, що хоча б двоє з них народилися в один день.

Розв’язання

Роль кроликів у цій задачі відіграють учні, а роль кліток – дні. За умовою задачі маємо 400 учнів і 365 днів.

Оскільки 400 > 365, то принаймні знайдеться два учні, що народилися в один день.

Задача 4. Хлопчик мав 100 табличок з числами 1, 2, 3, …, 100, але загубив 79 з них. Чи обов’язково серед решти табличок знайдуться чотири такі, що сума чисел на двох із них дорівнюватиме сумі чисел на двох інших?

Розв’язання

У хлопчика залишилася 100 – 79 =21 табличка. Із цих табличок можна утворити: різних пар. (Кроликами є пари, а клітками – суми).

Оскільки усі пари з чисел 1, 2, …, 100 дають 197 різних сум – від 3 до 199 і 197 < 210, то принаймні у двох парах із 210-ти суми співпадатимуть. Отже, серед табличок знайдеться чотири такі, що сума чисел на двох із них дорівнюватиме сумі чисел на двох інших.

Задача 5. В класі навчається 30 учнів. В диктанті 1 учень зробив 13 помилок, а інші — менше. Довести, що є принаймні 3 учні, що зробили однакову кількість помилок.

Доведення
1 учень відділений в умові, тоді учнів 30—1 = 29. Помилок може бути від 0 до 12, тобто їх кількість — 13. Припустимо, що не більше 2-х учнів зробили однакову кількість помилок, тоді всього в класі (13*2=26) — не більше 26 учнів, а це суперечить умові, адже їх 29. Отже, наше припущення хибне, і в класі є хоча б 3 учні, що зробили однакову кількість помилок.

Задача 6. У місті більше ніж 8 мільйонів жителів. Науковці вважають, що в кожної людини менш ніж 200 000 волосин на голові. Доведіть, що є принаймні 41 житель з однаковою кількістю волосин на голові.

Доведення.
Оскільки 40-200000 = 8000000 (кількість волосин у людини коливається від 0 до 199 999, всього 200 000 варіантів), то, згідно з принципом Діріхле знайдеться принаймні 41 житель, що має однакову кількість волосин на голові. Тут роль предметів відіграють жителі, а роль ящиків — усі можливі варіанти кількості волосин на голові.

Задача 7. Доведіть, що серед 82 кубиків, кожен із яких помальовано певним кольором, існує 10 кубиків різного кольору або 10 кубиків одного кольору.

Доведення.
Якщо для розмалювання 82 кубиків використано не менше ніж 10 кольорів, то зрозуміло, що знайдеться 10 кубиків різного кольору. Якщо ж для розмалювання 82 кубиків використано не більше ніж 9 різних кольорів, то, згідно з принципом Діріхле, знайдеться принаймні 10 кубиків одного кольору. Тут у ролі предметів виступають кубики, а в ролі ящиків — кольори.

Задача 8. У класі навчається 29 учнів. Сашко Петренко зробив у диктанті 13 помилок, і ніхто інший не зробив більшої кількості помилок. Довести, що принаймні три учні зробили однакову кількість помилок.

Розв’язання
Приймемо за «клітки» всі можливі варіанти кількості помилок. їх 14, оскільки учні можуть зробити 0, 1, …, 13 помилок. «Зайцями» вважатимемо учнів, які писали диктант і яких за умовою 29. Кожного з них «садимо» у «клітку», що відповідає кількості зроблених помилок. Зрозуміло, що знайдеться «клітка», в якій «сидять» принаймні три «зайці», а це й означає, що знайдуться три учні, які зробили однакову кількість помилок.

Урок №3

Задачі на подільність

Завдання 1.

Виконати письмово вправи:

Не перемножуючи, встановіть чи ділиться добуток 148·75 на 2, на5, на 10.

Розв’язання.

Оскільки 148 ділиться на 2, то добуток ділиться на 2. Оскільки 75 ділиться на 5, то добуток ділиться на 5. Оскільки 148 ділиться на 2, а 75 ділиться на 5, то 148·75 ділиться на 2·5 = 10.

В садовому центрі можна придбати оптом декілька видів розсади ранніх томатів, які мають різну кількість в упаковці: сорт Євгенія (50 шт), сорт Аврора (65 шт), сорт Червоне сонечко (73 шт), сорт Маленький принц (68 шт.), сорт Адмірал (60 шт.), сорт Царськосельський (58 шт). Який вид розсади томату треба придбати господарю для висадки, щоб розподілити їх в теплиці без остачі на 5 рядків?

Розв’язання. Оскільки на 5 діляться числа 50, 65 та 60 (які закінчуються 5 або 0), то господарю можна придбати наступні сорти: Євгенія, Аврора, Адмірал, щоб розсадити їх у 5 рядків без остачі.

Морозенко і Снігуронька придбали печиво, цукерки та мандарини. Яку найбільшу кількість однакових подарунків можуть зробити новорічні гості, маючи 128 печива, 192 цукерки та 160 мандарини?

Розв'язання. Знаходимо найбільший спільний дільник чисел 132, 162, 72.

128 2 192 2 160 2

64 2 96 2 80 2

32 2 48 2 40 2 НСД(128, 192, 160) = 32 (подар.)

16 2 24 2 20 2

8 2 12 2 10 2

4 2 6 2 5 5

2 2 3 3 1

1 1

Два туристичні автобуси вирушили з пункту А в одному напрямку. Перший автобус робить зупинки через кожні 36 км, а другий – через кожні 63 км. Яку найменшу відстань повинні проїхати ці автобуси, щоб їх зупинки співпали?
До кіоску з квітами завезли троянди. Якщо розкласти їх у вази по 15 або по 20 штук, то в обох випадках зайвих квітів не залишиться. Яку кількість квітів могли завезти до кіоску? Яка найменша кількість квітів могла бути завезена?

Розв'язання

Числа, кратні 15: 15, 30, 45, 60, 75, 90, 105, 120…

Числа, кратні 20: 20, 40, 60, 80, 100, 120…

Спільні кратні: 60, 120…

Найменше спільне кратне – 60.

НСК (15, 20) = 60 (квітів).

Уроки № 4, 5

Старовинні задачі на грошові розрахунки, на подорожі, на розрахунки в часі

Завдання 1.

Письмово виконати вправи:

Помирав старий араб. Все його багатство складалося з 17 прекрасних білих верблюдів. Він зібрав своїх синів і оголосив їм останню волю: «Старший, опора в сім’ї, повинен отримати половину моїх верблюдів. Середньому заповідаю третину, але мій найменший, улюблений, повинен отримати дев’яту частину отари». Поховавши батька, стали брати ділити тварин. Але виконати волю батька їм ніяк не вдавалось. Саме тоді пустелею проходив мудрець, який допоміг їм вирішити проблему. Як йому це вдалось?

Розв’язання. Из книги:

Мудрый старый араб добавил одного своего верблюда, чтобы их стало 18. Тогда всё хорошо делится:
1/2 от 18 = 9 верблюдов - старшему сыну

1/3 от 18 = 6 верблюдов – среднему

1/9 от 18 = 2 верблюда - младшему

Сумма получается 9+6+2=17. Оставшегося своего верблюда араб забрал себе.

У 15 ст. Христофор Колумб відкрив Америку. Дізнайтесь, в якому році це відбулось, якщо сума цифр цього року дорівнює 16, а результат від ділення цифри десятків на цифру одиниць дорівнює 4, а остача становить 1.

Відповідь: У 1492 році.

Група мудреців вирушила в похід. У перший день вони пройшли 1/3 шляху, в другий – 1/3 залишку, в третій – 1/3 нового залишку. В результаті їм залишилось пройти 32 км. Скільки кілометрів становив маршрут туристів?

Батьку і сину разом 65 років. Син народився, коли батькові було 25 років. Якого віку батько і син?

Одну вівцю лев з’їв за 2 дні, вовк – за 3 дні, собака – за 6 днів. За скільки днів вони разом з’їдять вівцю?

З табору вийшли чотири туриста: Василько, Галя, Толя і Леся. Василь йде попереду Лесі, Толя попереду Галі, а Леся попереду Толі. У якому порядку йдуть діти?

Три друга – Альоша, Сергій і Денис – купили цуценят різної породи: цуценя ротвейлера, цуценя коллі і цуценя вівчарки. Відомо, що: цуценя Альоші темніше за окрасом, ніж ротвейлер, Лесі та Гриф; щеня Сергій старше за Грифа, ротвейлера і вівчарки; Джек в ротвейлер завжди гуляють разом. У кого якої породи щеня? Назви клички цуценят.

Один купець купив 25% наявного шматка полотна, другий купець купив 30% залишку, а третій – 40% нового залишку. Скільки (у відсотках) полотна залишилось непроданим?

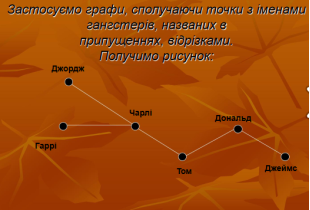
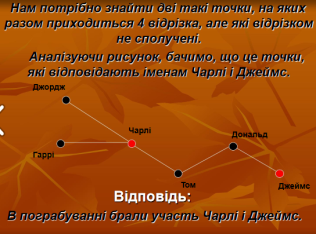
Відомо, що з 6 гангстерів двоє брали участь у пограбуванні. На питання, хто брав участь у пограбуванні дали такі відповіді:

Дональд: Том і Чарлі

Гаррі: Чарлі і Джордж

Чарлі: Дональд і Джеймс

Джеймс: Дональд і Том

Джордж: Гаррі і Чарлі.

Спіймати Тома не вдалось. Хто брав участь у пограбуванні, якщо відомо, що четверо гангстерів вірно назвали одного з учасників пограбування, а один назвав невірно обидва імені?

Уроки №6, 7

Задачі економічного характеру

Завдання 1. Усний рахунок.

1.Знайти 1 % від 80кг. ( 0,8кг)

2.Знайти 10 % від 150 грн. (15 грн)

3.Знайти 15 % від 100кг. (15кг)

4.Знайти 50 % від 120 т. (60 т)

5.Знайти 25 % від 40га. (10га)

6.Знайти 20 % від 800 грн. ( 160 грн)

7.Поділити 100 грн. пропорційно до чисел 2, 3, 5. (20 грн, 30 грн, 50 грн)

8.Скільки гривень одержить клієнт банку від 100 грн, якщо банк виплачує 25 % річних. (125 грн)

Завдання 2.

Математичний тест(перевірка в парах)

Кожне завдання тесту по 1 балу. В сум і- 6 балів.

Клас_____Прізвище,ім”я_____________	Клас______Прізвище,ім”я_____________
ВАРІАНТ 1		ВАРІАНТ 2
1.Знайди відношення: 5 м до 2 м а) 2,5 м; б) 5м:2; в)2,5 г) 2. Знайди невідомий член пропорції: 24 : 6 = 20 : х а) 5; б) 4; в) 120; г) 3. Яка з пропорцій є правильною? а) 36 : 6=72 : 12; б) 24 : 6=12 : 2; в) 36 : 9=27 : 3; г) 30 : 5=40 : 8. 4.Автомобіль за 1 год проїхав 65 км. Який шлях він проїде за 3 год, рухаючись із такою ж швидкістю? а)1625 км; б)195 км; в)162,5 км/год;г)26 км. 5. Для учнів двох шостих класів купили 153 зошити. Як розділити ці зошити між класами, якщо у 6-А класі навчається 25 учнів, а в 6-Б - 26 учнів? а) 50 і 75; б) 50 і 103; в) 75 і 78; г) 103 і 50. 6.Розділили 720 грн на три частини пропорційно до чисел 6,2,1. а)480 грн, 160 грн, 80 грн; б)10 грн, 340 грн, 370 грн; в)450 грн, 140 грн, 130 грн; г)40 грн, 230 грн, 450 грн.		1. Знайди відношення: 12 м до 3 м а) 4 м; б) 6:1; в) 12м : 3; г) 4. 2.Знайди невідомий член пропорції: 28 : 7 = х : 14 а) 56; б) 4; в) 2; г) 5,6. 3.Яка з пропорцій є правильною? а) 14 : 42=3 : 1; б) 1: 3=14 : 42; в) 3 : 1=14 : 42; г) 7 : 3=14 : 9. 4.За 3 м тканини заплатили 72 грн. Скільки грошей коштуватиме 1 м цієї тканини? а) 225грн; б) 24 грн; в)112,5грн;г)23,5грн. 5.Два робітники виготовили відповідно 15 і 16 деталей. Як розподілити між цими робітниками заробіток у 620 грн? а) 300 грн і 320 грн; б) 340 грн і 280 грн; в) 230 грн і 390 грн; г) 510 грн і 110 грн. 6.Розділили 1080 на частини пропорційні до чисел 5, 3, 1. а) 720, 340, 20; б) 600,360,120; в) 80, 360, 640; г) 450, 450, 180.

Відповіді до тесту:

Варіант 1 Варіант 2

в 1. г
а 2. а
а 3. б
б 4. б
в 5. а
а 6 .б

Завдання 3.

Задача від фермерів. Сім’я Петренків на літо взяла обробити поле цукрових буряків. Тато Петренко обробив 50 рядків , мама Петренко обробила 30 рядків, а синок Петрик Петренко обробив 10 рядків. За літо сім’я Петренків за обробку поля заробила 1800 гривень. Як ці гроші треба поділити між татом, мамою та їх сином?

Розв’язання.

Нехай – коефіцієнт пропорційності (вартість обробки одного рядка), тоді тато заробив 50 (грн), мама – 30(грн), син – 10 (грн). А за умовою задачі разом вони заробили 1800 грн.

Маємо рівнянняя:

50+30+10=1800;

90=1800;

=1800:90;

=20.

Отже, татова частина грн; мамина - грн; синова - грн.

Відповідь: 1000 грн, 600 грн, 200 грн.

Задача від хіміків. Сплав складається з міді, олова і сурми, які взято у відношенні 1: 2 :2. Знайдіть масу сплаву , якщо він містить 2,8 кг олова.

Розв’язання.

Відношення 1 : 2 : 2 означає, що у сплаві на мідь припадає 1 частина, на олово – 2 таких самих за масою частини, на сурму – 2 частини.

Сплав складається з 1+2+2=5 частин, з яких на на олово припадає 2 частини.

Нехай маса сплаву дорівнює х (кг), тоді маємо пропорцію:

5 частин – х кг;

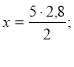
2 частини – 2,8 кг.

(кг).

Отже, маса сплаву 7 кг.

Відповідь: 7 кг.

Задача 3. Сергійко бажає у подарунок на Новий рік мобільний телефон за 5500 грн. Зараз магазин пропонує купити цей телефон зі знижкою 15 %. Скільки коштує новий телефон?

100 – 15 = 85% - складає нова ціна
5500 грн. – 100%

х грн. – 85 %

Задача 4. Скільки коштує нова сукня для Маші, якщо після підвищення його ціни на 15% воно стало коштувати 345 грн?

100 + 15 = 115 % - складає вартість сукні
100 % – х грн.
115 % – 345 грн.

Задача 5. Банк надає кредит 30000 грн. зі ставкою 10% річних. Яку суму потрібно повернути банку через 2 роки?

100 + 10 = 110% - потрібно повернути через 1 рік
30000 грн – 100%

х грн. – 110 %

– потрібно повернути через 1 рік

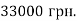– 100%

– 110 %

Завдання 3.

Клас ділиться на групи для самостійної роботи.

Самостійна робота.

Будівельники

Задача 1.Щоб виготовити замазку, беруть вапно, житнє борошно, олійний лак у відношенні 3: 2: 2. Скільки потрібно взяти кожного матеріалу, щоб мати 4,2кг замазки? (3 бали)

Розв’язання.

кг вапна

кг житнього борошна

кг олійного лаку

Відповідь: 1,8кг вапна, 1,2кг житнього борошна, 1,2кг олійного лаку.

Задача 2.Визначити скільки потрібно взяти цементу, піску й щебеню для виготовлення 140м³ бетону, якщо за об’ємом вони знаходяться у відношенні 1:2:4? (3 бали)

Розв’язання.

цементу,

піску,

щебеню.

Відповідь: 20м³ цементу, 40м³ піску, 80м³ щебеню.

Банкіри

Задача 1. Поклавши до банку 1100 грн, через рік клієнт отримав відсоток, що становить 88 грн. Скільки відсотків річних сплачує цей банк? (2 бали) Розв’язання.

1100 грн – 100%

88 грн – х%

Відповідь: 8% річних.

Задача 2. Вкладник поклав до банку 1000 грн, а через рік одержав 1180 грн. Скільки відсотків річних сплачує банк? (3 бали)

Розв’язання.

1000 грн – 100%

1180 грн – х%

118% - 100% = 18%

Відповідь: 18% річних.

Бухгалтери

Задача 1. Службовець сплачує медичну страховку у розмірі 120 грн., що становить 15 % його заробітної плати. Яка заробітна плата у службовця? (3 бали)

Розв’язання.

120 грн – 15%

х грн. - 100%

Відповідь: 800 грн.

Задача 2. За деяку роботу робітникові нарахували 2395 грн. Із них

13 % - прибутковий податок,

2 % - відрахування у пенсійний фонд,

1 % - відрахування у фонд зайнятості,

1 % - профспілковий внесок.

Скільки одержить працівник після всіх відрахувань? (3 бали)

Розв’язання.

13+2+1+1=17%

100%-17%=83%

2 395 грн – 100%

х грн – 83%

грн

Відповідь: працівник одержить 1987,85 грн.

Кулінари

Задача 1. З 0,3 т свіжих яблук виходить 57кг. сушених. Скільки можна одержати сушених яблук з 2,1 т свіжих? (3 бали)

Розв’язання.

57кг = 0,057 т

0,3т – 0,057 т сушених яблук

2,1т – х т сушених яблук

т сушених яблук

Відповідь: 0,399 т сушених яблук.

Задача 2. 100кг цукру треба поділити пропорційно числа 9, 8 і 3 для випічки печива, для приготування кремів та для морозива. (3 бали)

Розв’язання.

цукру для печива

цукру для кремів

цукру для морозива

Відповідь: 45кг цукру для печива, 40кг цукру для кремів, 15кг цукру для морозива.

Пекарі

Задача 1.За 5 год. у млині змололи 45 т. борошна. Скільки тонн борошна можна змолоти за 7 год.? (3 бали)

Розв’язання.

5 год – 45 т борошна

7 год – х т борошна

Відповідь: 63 т борошна.

Задача 2.З 2 ц пшениці одержали 1,8 ц борошна. Скільки пшениці треба заготовити, щоб за тих самих умов мати 1 т борошна? (3 бали)

Розв’язання.

1 т = 10 ц

2 ц пшениці – 1,8 ц хліба

х ц пшениці – 1 ц хліба

ц пшениці

Відповідь: ц пшениці.

Промисловці

Задача 1. З 0,5 т руди можна виплавити 0,3 т чавуну. Скільки тонн чавуну можна виплавити з 3 т руди? (3 бали)

Розв’язання.

0,5 т руди – 0,3 т чавуну

3 т руди – х т чавуну

Відповідь: 1,8 т чавуну.

Задача 2. Для виготовлення порцеляни беруть 25 частин глини білої, 2 частини піску і одну частину гіпсу. Скільки кожного з цих матеріалів треба взяти, щоб отримати 280кг суміші, з якої виготовляють порцеляну? (3 бали)

Розв’язання.

білої глини