Балинська  ЗОШ І-ІІІ ступенів

 

 Нізевич А.С.

 

 

 

 

 

 

 

 

 

 

 

 

Рецензенти: Сікора М.М. – методист Методичного сервісного центру

Левчук Л.Б. – заступник директора з навчально-виховної роботи Балинської ЗОШ І-ІІІ ст.

 

 

 

 

 

 

 

 

Рекомендовано до друку засіданням Методичного сервісного центру (протокол № 4 від 20 грудня 2016 р.)

 

 

 

 

 

 

 

 

 

 

Рекомендовано вчителям математики, учням

Зміст

Передмова

Тригонометрія: історія зародження та професійне спрямування

Тригонометрія: прикладні задачі

Логарифмічна та показникова функції: історія зародження та застосування у різних галузях

Логарифмічна та показникові функції: прикладні задачі

Похідна функції: історія зародження та застосування у різних галузях

Похідна функції: прикладні задачі

Первісна та інтеграл: історія зародження та застосування у різних галузях

Первісна та інтеграл: прикладні задачі

Список використаних джерел

Передмова

 

Як відомо, математика виникла з практичних потреб людини. Тому, де б ми не були, який би предмет не вивчали, в якій би галузі не працювали – скрізь потрібні знання з математики. Сьогодні, як ніколи, стоїть гостра потреба в підготовці робітничих кадрів. Знань, які одержують учні на уроках із спецдисциплін, недостатньо, щоб бути конкурентноспроможним на ринку праці. Велику роль у професійному формуванні спеціаліста відіграють прикладні задачі з математики.

У сучасному світі математика відіграє велику роль у теоретичних, технічних, економічних дослідженнях. Багато економічних проблем, наприклад, проблем внутрішнього зв’язку прогнозів, їх оптимізація, вибір найефективніших інвестиційних рішень та інше може бути успішно розв’язане за допомогою математичних методів.

При вивченні курсу математики у старшій школі, незважаючи на кількість аудиторних годин, потрібно приділяти багато уваги розв’язанню прикладних задач, які є важливим фактором формування в учнів наукового світосприйняття. Також розв’язування прикладних задач збагачує школярів теоретичними знаннями, формує навички і вміння застосовувати математичні знання на практиці. Це важливо тому, що чимало учнів не завжди розуміють безпосередній зв’язок математичних теорій із природними явищами.

Прикладні задачі допомагають активізувати пізнавальну діяльність студентів, підвищують їхній інтерес до вивчення предмета, забезпечують розвиток здібностей до технічної творчості, формують навички відшукування раціональних шляхів розв’язування поставлених задач. Ці завдання сприяють створенню на заняттях проблемних ситуацій, можуть бути засобом повідомлення й обґрунтування теми заняття тощо.

Прикладна задача – задача, яка виникла поза математикою, але розв’язується математичними засобами і повинна задовольняти такі умови:

- питання задачі формулюється так, як воно зазвичай формулюється в житті;

- розв’язок задачі має практичну значимість;

- дані та шукані величини задачі мають бути реальними, взятими з життя.

Прикладне спрямування математики і лягло в основу нашого проекту, а значимість його можна підкреслити крилатими словами Леонардо да Вінчі: «Ніяке людське дослідження не може бути названо істиною, якщо воно не проходить через математичні доведення».

Щоб максимально приблизити знання, уміння і навички наших учнів до використання цих знань у майбутній професійній діяльності, велика увага приділяється підбору прикладних задач, які взято з реального життя.

Тригонометрія: історія зародження та професійне спрямування

 

Причини зародження тригонометрії

Наприкінці ХV ст. італійський мандрівник Христофор Колумб відкрив узбережжя Америки. Слідом за ним туди зробив кілька подорожей інший італієць – Америго Віспуччі. Португалець Васко да Гама відкрив морський шлях на Індію. Незабаром кораблі Магеллана вперше в історії зробили навколосвітню подорож. Почалася епоха великих географічних відкриттів, завоювань нових територій, освоєння незліченних багатств нових земель.

Не тільки окремі групи купців і мореплавців, але і цілі держави боролися за право експлуатації нових земель. Потрібні були більш потужні і швидкохідні судна, точні географічні карти, досконалі способи орієнтування в відкритому океані.

Створити все це неможливо було без точного математичного розрахунку. Для виконання цих розрахунків елементарної геометрії Евкліда часто не вистачало. Необхідні були нові способи, нові методи в математиці, і, зокрема, в геометрії.

Все це і багато чого іншого привело до необхідності розвивати астрономію – науку про рух небесних тіл, а розвиток астрономії був неможливий без розвитку тригонометрії.

 

Перші кроки тригонометрії

Слово “тригонометрія” складається із двох грецьких слів: “триганон” – трикутник і “метрайн” – вимірювати. У буквальному значенні “тригонометрія” означає “вимір трикутників”.

Астрономія, а разом з нею і тригонометрія виникли і розвивалися в народів з розвиненою торгівлею і сільським господарством: у вавілонян, греків, індійців, китайців. Зародилася вона багато століть тому. Про це ми можемо не тільки здогадуватись.

В одному з китайських рукописів, що був написаний близько 2637 року до н.е., є відомості з астрономії, де застосовуються обчислення тригонометричного характеру.

Вавилоняни вже на початку  III тисячоліття до н.е. мали календар з розподілом року на 12 місяців. Отже вони вміли визначати положення сонця і зірок на небосхилі, тобто володіли певними знаннями тригонометричного характеру.

Велике значення для розвитку тригонометрії в період її зародження мали праці грецьких учених.

Протягом тисячі років тригонометрія була підсобною наукою у астрономії.

Складалися нові таблиці, знаходилися нові залежності між тригонометричними функціями, за допомогою яких розв’язувалися складні задачі, але тригонометрія залишалася тільки частиною астрономії, самостійної науки не існувало.

 

Вклад вчених в розвиток тригонометрії

У IX – XV ст. на розвиток тригонометрії великий вплив зробили народи, що населяли територію теперішніх середньоазіатських країн, країн Закавказзя, Іраку, Афганістану і Сирії.

Аль–Хорезмі (IX ст.) систематизував індійські таблиці тригонометричних величин.

Абуль–Вефа (940 – 998рр) склав таблиці синусів через кожні 10 мінут.

Вінцем досягнень середньоазіатських вчених у галузі тригонометрії можна вважати відділення її від астрономії і виокремлення в самостійну науку. Головна заслуга в цьому належить азербайджанському вченому Насиреддіну Тусі (1201 – 1274рр). У його праці ми вперше зустрічаємо доведення теореми синусів і теореми тангенсів.

У складанні тригонометричних таблиць видатних успіхів досяг узбецький вчений з м. Самарканда Аль–Каші (помер близько 1430р.). Він обчислив таблиці синусів з точністю до однієї мільярдної. Це були найточніші таблиці на той час.

Німецький математик Йоган Мюллер (1436 – 1476) першим з європейських учених дав послідовний виклад тригонометрії, обчислив дуже точні таблиці синусів і тангенсів.

Багато для розвитку тригонометрії зробили й інші вчені. Завдяки праці кількох поколінь учених тригонометрія стала самостійною наукою.

Завершальний етап у розвитку тригонометрії пов'язаний з ім’ям Леонарда Ейлера.

Заняття астрономією, географією і морехідними науками неможливі без застосування тригонометрії. Але до початку XVIII ст. вона була наукою неопрацьованою, часто незручною в роботі, що іноді призводило до помилок. Це змусило Ейлера переглянути доведення тригонометричних формул. Він упорядкував питання про знаки тригонометричних функцій у різних чвертях, ввів однакове позначення сторін трикутника: а, в, с і протилежних кутів А, В, С.

Ейлер розробив тригонометрію як науку про тригонометричні функції.

У працях Ейлера тригонометрія набула сучасного вигляду. На підставі його робіт були укладені підручники з тригонометрії, що викладають її в строгій науковій послідовності.

 

Тригонометрія та професія судноводія (штурмана)

Штурман, судноводій, навігатор в перекладі з латинської – людина, «що може ходити по морю», «їздити по морю». В давнину судноводії приводили кораблі в потрібне місце, користуючись найпримітивнішими засобами. Тому довгий час основними районами плавання залишались прибережні. В плавання, як правило, вирушали влітку, коли небо було безхмарним, вдень світило сонце, а вночі були добре видні зірки. Перша згадка про морські карти відноситься до 490 р. до н.е. Вони були дуже примітивними і скоріше нагадували креслення. Потреба мореплавців у плаваннях далеко від берегів поставили питання про подальше вдосконалення морських карт, морехідних приладів, висунули на перший план проблему астрономічних спостережень. Тому важливим кроком став винахід інструмента для визначення висоти світил – астролябії (Х ст.).

В ХІІ ст. в Європі з’явився магнітний компас. В XV ст. була винайдена лінійка Герсона- кутомірний прилад, який був більш точним, ніж астролябія.

Застосування цих приладів здійснило революцію в навігації. За допомогою них мореплавці могли орієнтуватися в будь-яких районах Світового океану. Почалася епоха великих географічних відкриттів. Великі морські плавання значно збагатили науку і вплинули на подальший розвиток астрономії, навігації, топографії – основних складових науки про судноводіння.

Навігація вирішує питання визначення напрямів і пройденої відстані в морі; методи обчислення шляху і способи визначення місця судна в морі по береговим і плавучим орієнтирам за допомогою штурманських приладів; питання керування і безаварійної проводки судна при особливих умовах плавання.

Морехідна астрономія вирішує питання визначення місця судна в морі за положенням небесних світил.

Картографія допомагає за допомогою теорії картографічних проекцій, що застосовується в судноводінні, розв’язувати аналітичними і графічними способами специфічні штурманські задачі по проведенню судна з врахуванням дії різних факторів( вітру, течії і т.д.).

Всі ці науки побудовані на строгій математичній основі. Але конкретні обставини на морі, інколи дуже складні, не завжди дозволяють штурману отримати необхідну інформацію з потрібною точністю навіть за допомогою сучасних технічних засобів. Тому судноводіння, побудоване на науково-математичній основі, забезпечує безпеку судна при плаванні в будь-яких умовах.

Уміння здійснити плавання найзручнішим в даних умовах шляхом, найбільш точно провести судно в порт призначення, з необхідною точністю визначити місце судна в морі практично на будь-яких відстанях – все це залежить від судноводія. І всі ці задачі вирішуються з застосуванням знань з тригонометрії.

Тригонометрія: прикладні задачі

 

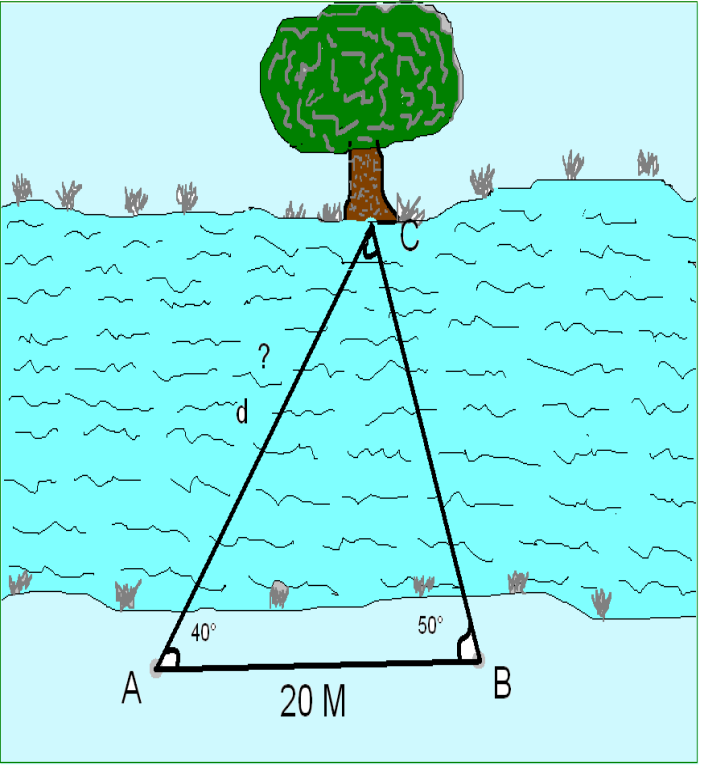
№ 1. Знайти відстань від точки А до дерева, яке росте на другому березі річки, якщо з точки А видно це дерево під кутом 40° до лінії берега річки, а з точки В під кутом 50° і відстань між точками А і В дорівнює 20м.

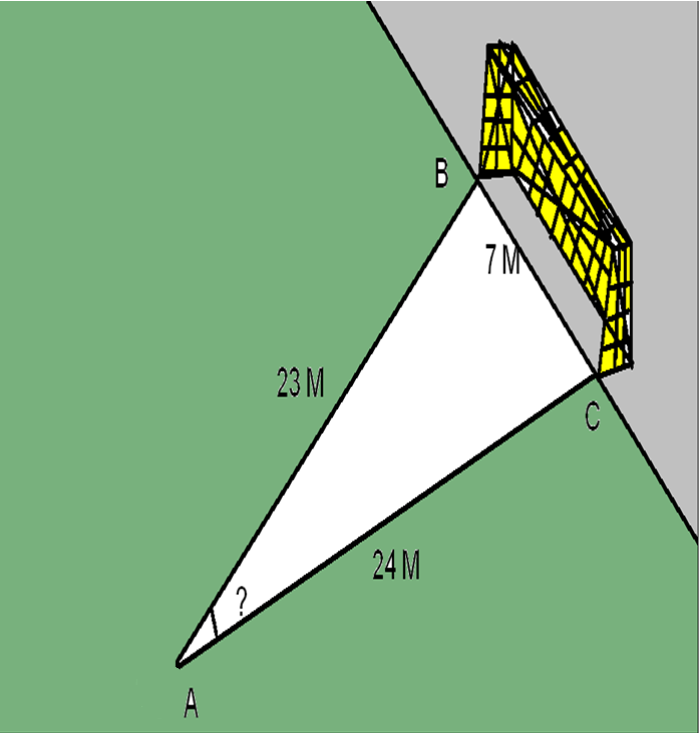
№2. Футбольний м’яч знаходиться в точці А футбольного поля на відстані 23м і 24м від точок В та С відповідно. Футболіст направив м’яч у ворота. Знайдіть кут влучання м’яча у ворота, якщо ширина воріт 7м.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

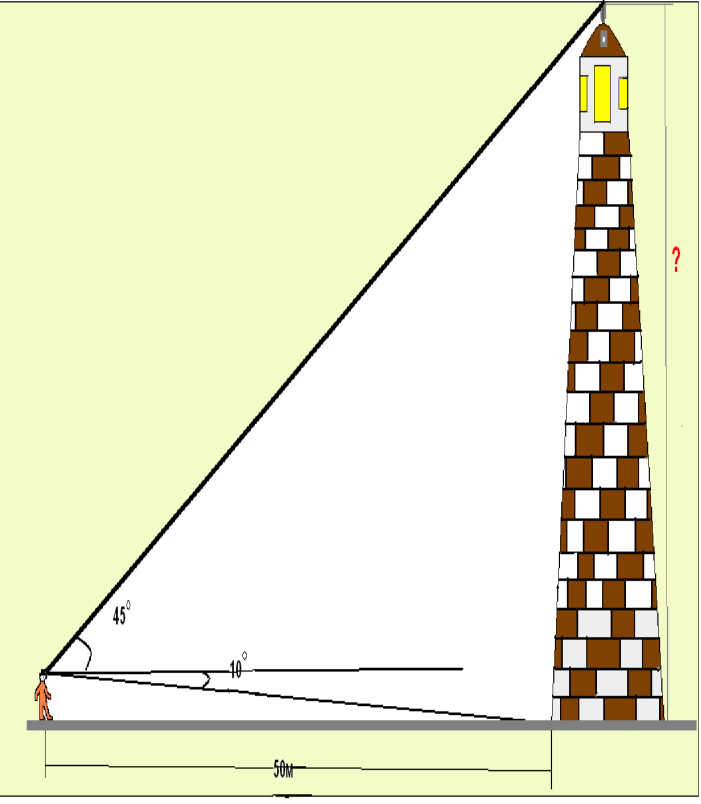
№3. Спостерігач знаходиться на відстані 50м від вежі, висоту якої хоче знайти. Основу вежі він бачить під кутом 10° до лінії горизонту, а вершину під кутом 45° до лінії горизонту. Яка висота вежі?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

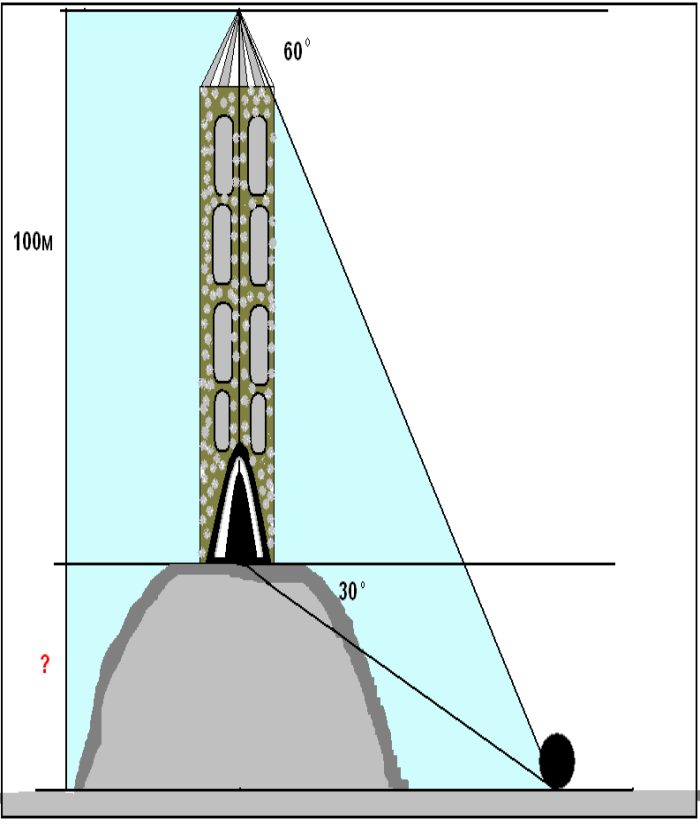
№ 4. На горі побудована вежа, висота якої 100м. Біля підніжжя гори лежить камінь. Цей камінь видно з вершини вежі під кутом 60° до горизонту, а з входу в вежу – під кутом 30° до горизонту. Знайдіть висоту гори.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

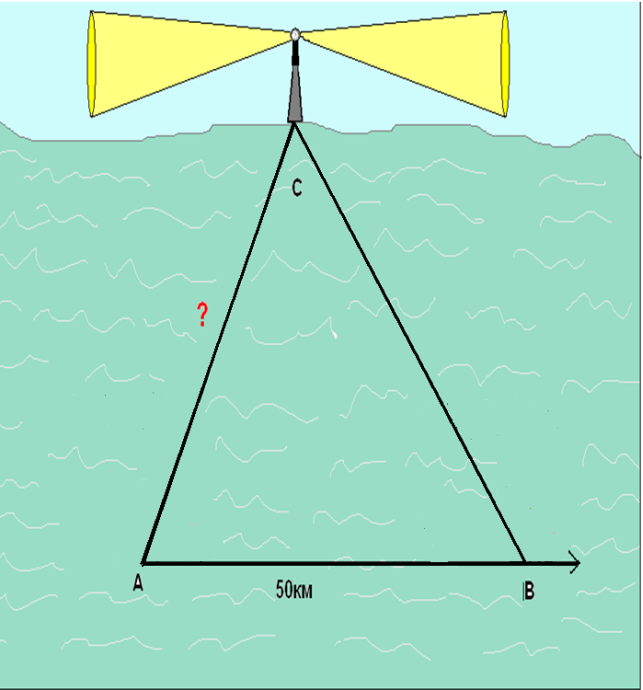
№ 5. Знайти відстань від точки А, в якій знаходиться корабель в певний момент часу до маяка на березі, якщо з цієї точки видно  видно маяк під кутом 60° до курсу , а через деякий час корабель буде знаходитись в точці В –  на відстані 50 км від точки А, і з точки В даний маяк видно під кутом 110° до курсу корабля.

 

 

 

 

 

 

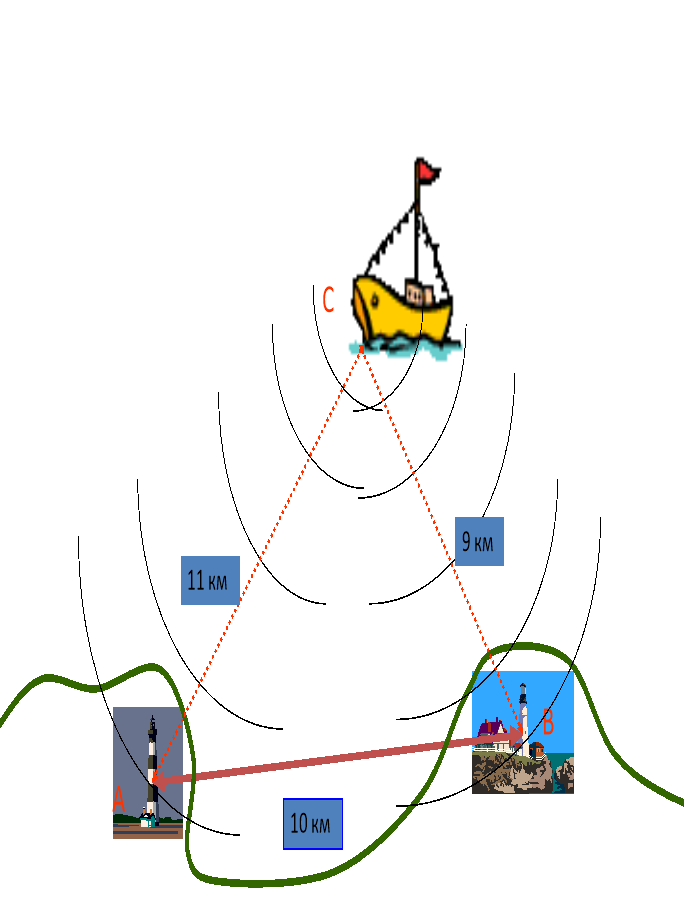
№ 6. Берегові радіомаяки А і В розміщені на відстані 10 км один від одного. З теплоходу С, за допомогою радіолокаційної станції, що знаходиться на ньому. Визначені відстані до маяків СА=11 км і СВ=9км. Знайдіть кути САВ і СВА пеленгів радіомаяків.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

№ 7. Два теплохода А і В, що знаходяться в відкритому морі на відстані 20 км один від одного, одночасно отримали сигнал sos з корабля С.

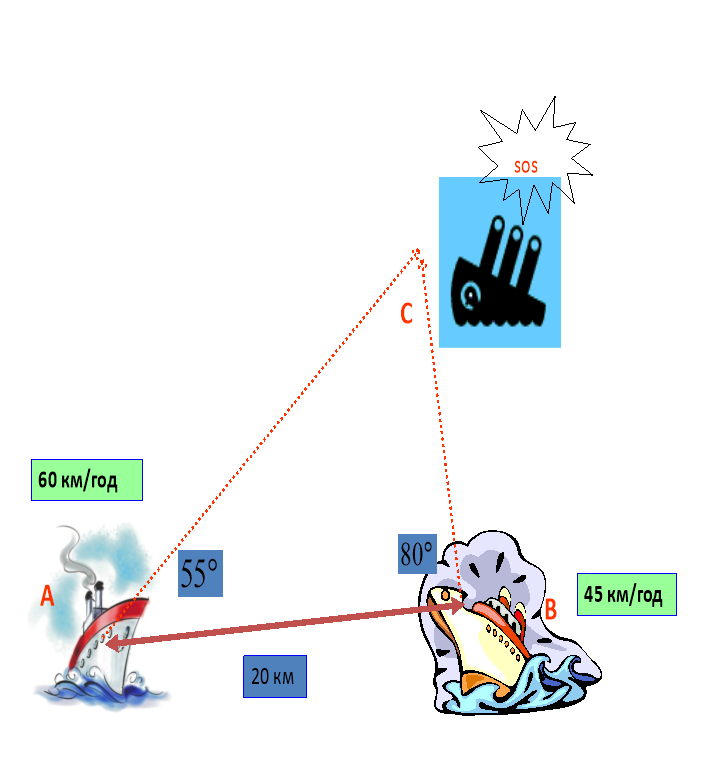Радіопеленг по відношенню до прямої АВ на судні А дорівнює 55 градусів, а на судні В – 80 градусів.

Який теплохід першим прийде на допомогу, якщо максимальна швидкість судна А - 60 км/год, а судна В - 45 км/год?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Логарифмічна та показникова функції: історія зародження та застосування у різних галузях

 

Найперші зародки поняття логарифма можна знайти в Архімеда, але сама ідея розвитку не набула. Триста років тому в епоху Відродження почався бурхливий розвиток науки, техніки і мореплавства. Розвиток астрономії, а точніше астрономічних спостережень, вимагали нових методів обчислень, які були б доступні широкому колу людей. В основу таких методів і були покладені логарифми.

Логарифм – з грецької  означає “логос”- відношення і “аритмос”-  число.

Його винахід пов’язаний з двома постатями: швейцарцем Іобстом Бюргі(1552-1632), знаним годинникарем і майстром майстром астрономічних інструментів, і шотландцем Джоном Непером (1550-1617), який теж не був математиком за професією, астрономія була його «хобі». А Бюргі працював разом з астрономом Іоганном Кеплером. Саме величезний обсяг необхідних в астрономії обчислень і спонукав Бюргі і Непера шукати шляхів для їх спрощення. 20 років присвятив Непер своїм логарифмічним таблицям, аби, за його словами, «позбутися нудних і тяжких обчислень, відлякують зазвичай багатьох від вивчення математики». Обидва автори прийшли до своїх таблиць незалежно один від одного. Вони склали таблиці так званих натуральних логарифмів. Бюргі працював над таблицями 8 років і видав їх у 1620 році під назвою «Арифметична і геометрична таблиця прогресії». Проте його таблиці не отримали широкого поширення, бо Непер видав свій «Опис дивовижної таблиці логарифмів» на 6 років раніше. Тому і визнали число e неперовим числом.

Ідея десяткових логарифмів виникла у професора лондонського коледжу Генрі Брігса(1561-1630) після ознайомлення з таблицями Непера. Він двічі побував у Непера, здружився з ним і в процесі спільних занять обидва розробили нову, практично зручнішу десяткову систему, засновану на порівнянні прогресії.

Брігс взявся розробити велику таблицю десяткових логарифмів. Уже в 1617 р. він опублікував восьмизначні таблиці логарифмів від 1 до 10³, а в 1624 році спромігся  видати «Логарифмічну арифметику», що містила чотирнадцятизначні таблиці логарифмів для чисел 1-20000 і 90000-100000.

Понад три з половиною сторіччя з тих пір, як у 1614 році були опубліковані Непером перші логарифмічні таблиці, вони вірою і правдою служили астрономам і геодезистам, інженерам і морякам, скорочуючи час на обчислення і, як сказав французький вчений Лаплас (1749-1827), продовжуючи життя обчислювачам.

Ще донедавна важко було уявити собі інженера без логарифмічної лінійки в кишені. Винайдена в 1624 році англійським математиком Едмундом Гунтером (1581-1626), вона дозволяла швидко одержувати відповідь з достатньою для інженера точністю до трьох значущих цифр. І хоч тепер її витіснили калькулятори і комп’ютери, проте можна сміливо сказати, що без логарифмічної лінійки не було і перших комп’ютерів.

 

Логарифмічна спіраль – це крива, яка перетинає всі кути, що виходять із однієї точки О, під одним і тим же кутом α.

 Рівняння (в полярних координатах) має вигляд: .

 Таку криву описує рухома точка, відстань від полюса якої росте в геометричній прогресії, а кут, що описується її радіусом-вектором, - в арифметичній.

Характерні особливості логарифмічної спіралі:

•   Має нескінченну кількість витків як при розкручуванні так і при скручуванні;
•   Не проходить через свій полюс;
•   Її називають рівнокутною спіраллю;
•   В будь-якій точці спіралі кут між дотичною до неї та її радіус-вектором зберігає постійне значення;
•   При різних перетвореннях (гомотетії, повороті) вона залишається незмінною;
•   Має широке застосування в технічних приладах.
•   Властивості цієї кривої так вразили Якоба Бернуллі, що він назвав її spira mirabilis (чудова спіраль) і заповів зобразити її на його могилі з написом Eatemmutata resurgo (перетворювана, відроджуюся знову).

 

ФІЗИКА

 

Фізика завжди вимагає математичних розрахунків, тому знання математики у фізиці завжди необхідне. Ось декілька формул, де використовуються логарифми.

 

•              Робота, яку виконує газ при ізотермічному процесі

  

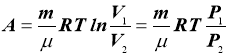
m – маса газу;

µ - молярна маса газу;

R – універсальна газова стала;

Т  – температура за Кельвіном;

V -  об’єм газу;

P – тиск газу.

•              ємність циліндричного конденсатора:

  

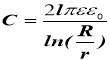
L – висота циліндра;

R, r – радіуси внутрішнього та зовнішнього циліндра;

 – техн. характеристики конденсатора;

•              Ємність дільниці одиничної довжини двох провідної лінії

  

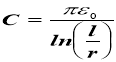
   r – радіус провідника

•              Зв’язок між сталою розпаду, середнім часом життя і періодом піврозпаду Т

  

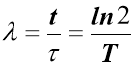
    – середній час життя;

   Т – період піврозпаду;

•              Рівень інтенсивності звуку

  

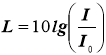
  - умовно нульовий рівень

•              Ентропія

  S=kln

К – стала Больцмана;

Ω - термодинамічна імовірність ;

S – ентропія;  

 

•              Зміна ентропії при ізотермічному стисканні газу

  

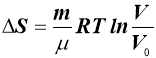
R – універсальна газова стала

µ - молярна маса газу

m – маса газу;

V – об’єм газу.

 

У техніці часто застосовуються ножі, що обертаються. Сила, з якою вони тиснуть на матеріал, що розрізається, залежить від кута розрізання, тобто кута між лезом ножа і напрямом швидкості обертання. Для того, щоб тиск був сталим, потрібно щоб залишався сталим кут розрізання, а це буде у тому випадку, коли леза ножів будуть окреслені по дузі логарифмічної спіралі. Завдяки цьому лезо ножа сточується рівномірно.

 

Якщо літак буде летіти, дотримуючись весь час одного курсу, тобто перетинаючи всі меридіани під одним і тим самим кутом, то його шлях зобразиться на карті логарифмічною спіраллю.

У гідротехніці по логарифмічній спіралі вигинають трубу, що підводить потік води до турбіни. Завдяки такій формі труби втрати енергії при зміні напряму течії в трубі виявляються мінімальними і напір води використовується з максимальною продуктивністю.

 

ХІМІЯ

 

Розчини в природі можуть мати різну реакцію середовища: кислу, лужну, нейтральну, що характеризується різною концентрацією йонів Гідрогену С(Н⁺).Для зручності датським біохіміком С.Сьоренсеном у 1909 році було введено термін «водневий показник» (рН), –це значно спростило роботу багатьом поколінням хіміків.

Водневий показник - це від'ємний десятковий логарифм концентрації йонів Гідрогену

рН= - lg С( Н⁺)

Значення рН може змінюватись від 1 до 14

Наприклад, С( Н⁺)=10^-7,рН=7;

  С( Н⁺)=10^-2 ,рН=2.

У нейтральному – рН=7.

У кислому середовищі рН<7, у лужному рН>7,

Показник рН в біологічних розчинах

Рідина	рН	Рідина	рН
Шлунковий сік	1,4	Сеча	6,0
Сік лимона	2,1	Слина,молоко	7,4-8
Сік яблук "Антонівка"	2,5	Слюзи	7,0
Томатний сік	4,1	Кров	7,4

З таблиці видно, що різні розчини в людському організмі мають різний рН, його відхилення від норми спричиняє захворювання і навіть загибель організму. Людям з підвищеною кислотністю шлункового соку рекомендується пити мінеральну воду з меншою концентрацією йонів Н⁺ (тобто з вищим рН), а зі зниженою кислотністю - "кислішу" воду (з нижчим рН).

Використовуючи різні засоби особистої гігієни, креми для шкіри, ліки, необхідно враховувати значення рН. Більшість рідких косметичних засобів має рН 5,5. Відповідний вміст у них катіонів Н⁺ оптимальний для нашої шкіри.

   

У сільському господарстві кислотність грунтового розчину є одним із головних чинників, що впливають на врожай. Так, картопля найкраще росте на слабокислих грунтах (рН≈5), а буряк на нейтральних (рН≈7).

 

БІОЛОГІЯ

 

Можна сказати, що спіраль є математичним символом співвідношення форми і зростання.

Великий німецький поет Йоганн-Вольфганг Гете вважав її символом життя і духовного розвитку.

Логарифмічна функція виникає у зв'язку з найрізноманітнішими природними формами. По логарифмічних спіралях розташовуються квітки в суцвіттях соняшника, закручуються раковини молюска Nautilus, роги гірського барана і дзьоби папуг. Один з павуків, епейра, сплітаючи павутиння, закручує нитки навколо центра по логарифмічним спіралям.

Нічні метелики, які пролітають величезні відстані, орієнтуючись по паралельним промінням місяця, інстинктивно зберігають прямий кут між напрямом руху і променем світла. Якщо вони орієнтуються на точкове джерело світла, інстинкт їх підводить, і метелики потрапляють в полум’я по логарифмічної спіралі, що скручується.

 

МУЗИКА

 

Розкопуючи одне з поселень кам’яного віку на території України, археологи знайшли кілька кісток мамонта, призначення яких було їм не зрозуміле. Лише уважний аналіз показав, що на цих кістках залишилися сліди ударів - це були залишки шумового оркестру, під звуки якого стародавні люди виконували магічні танці. Пізніше помітили, що більш приємні звуки можна отримати, зробивши барабан або просвердливши шматок дерева, щоб вийшла сопілка. А звучання тятиви лука? Воно навело на думку про створення струнних інструментів.

Піфагор був не тільки великим математиком, а й хорошим музикантом. Він встановив, що приємні сполучення звуків відповідають певним співвідношенням між довжинами струн, що коливаються, або відстаням між дірочками сопілки. Саме він створив першу математичну теорію музики, і хоча музиканти не дуже люблять перевіряти „алгеброю гармонію”, вони весь час мають справу з математикою, бо сучасна гама ґрунтується на логарифмах.

Будемо називати найнижчу октаву нульовою; а кількість коливань ноти do цієї октави за 1 секунду приймаємо за 1.Тоді нота do першої октави буде робити в два рази більше коливань. Позначимо всі ноти хроматичної гами номерами р , приймаючи за нульовий перший тон кожної гами. Тоді тон sol буде 7-й, la -9-й, 12-й тон буде знову do, тільки октавою вище.

Тому кожен наступний тон в разів має більше коливань, ніж попередній.

Позначимо Npm – кількість коливань тону з номером р із m-ї октави.

Nmp=2 ( )=2·2= 2+

Про логарифмуємо обидві частини останньої нерівності:

logNmp= m+

Звідси видно, що номери клавіш рояля являють собою логарифми кількості коливань відповідних звуків. Номер октави – характеристика (тобто ціла частина) логарифма, а номер звука в даній октаві - його мантиса (тобто дробова частина).

Логарифмічна та показникові функції: прикладні задачі

 

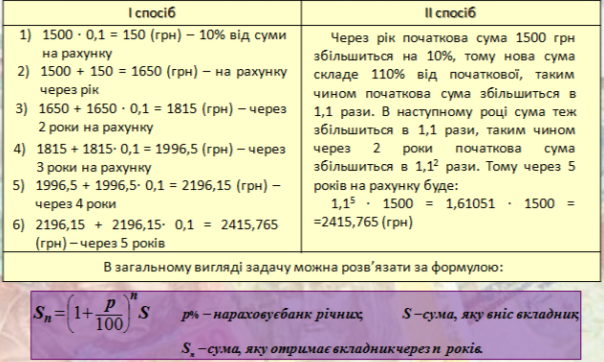
№ 1. Вкладник поклав на рахунок 1500 грн. Яка сума буде в нього через 5 років, якщо відсоткова ставка 10% річних?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

№ 2. При оформленні кредиту в розмірі 10000 грн на півроку під 10% річних були отримані комісійні в розмірі 1% від суми кредиту. Яка фактично використана сума кредиту і під який відсоток річних був фактично оформлений кредит?

 

 

 

 

 

 

 

 

 

 

 

 

 

№ 3. 1 січня 2015 року бізнесмен вирішив питання про придбання копіювально-розмножувальної техніки на суму 55 млн. грн. Термін придатності техніки – 3 роки, після чого вона повністю зношується. Щорічний прибуток від використання – 25 млн. грн. Щорічні витрати на її використання розподіляються за роками наступним чином: 2, 3 та 4 млн. грн. при цьому прибуток отримуємо в кінці року, а відповідні витрати на використання виплачуються одразу при отриманні прибутку. Техніку, що придбали, продати не можливо. Чи є смисл у придбанні техніки при умові, що ставка банківського прибутку за депозитом (виплачується один раз на рік) до 1 січня 2018 року буде постійною та складає 10% на рік? Інфляція у рахунок не приймається.

 

 

 

 

 

 

 

 

 

№ 4. Вкладник поклав до банку 10000 грн під 12% річних. Через скільки років сума на рахунку подвоїться?

 

 

№ 5. Населення міста зростає щорічно на 3%. Через скільки років населення міста збільшиться у 5 разів?

 

 

 

 

 

 

 

 

 

 

 

№ 6. Якою була чисельність населення міста 10 років тому, якщо в даний час проживає 300 тис. чоловік, а щорічний приріст населення складає 3,5%?

 

 

 

 

 

 

 

 

 

 

№ 7. Обчислити яким буде атмосферний тиск на вершині Ельбрусу, висота якого 5,6 км, якщо залежність атмосферного тиску від висоти (вираженої в км) над рівнем моря виражається формулою .

 

 

 

№ 8. Альпіністи, які підкорювали пік Перемоги, досягли висоти, де тиск був рівний 304 мм рт. ст. Обчислити, на якій висоті знаходились альпіністи, якщо мм рт. ст.

 

№ 9. Обчислити вартість обладнання в гривнях через 5 років, якщо його початкова вартість 4,68·10⁵ грн, а щорічний відсоток амортизації 5,7%.

 

 

 

 

 

 

 

 

 

 

 

 

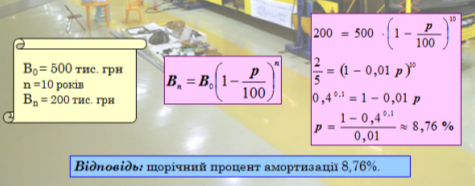
№ 9. Вартість обладнання дорівнює 500 тис. грн. Відомо, що через 10 років вартість цього обладнання внаслідок амортизаціх буде рівна 200 тис. грн. Знайти відсоток щорічної амортизації обладнання.

 

 

 

 

 

 

 

 

 

 

 

 

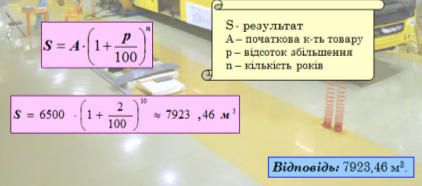
№ 10. Ділянка лісництва складає 65000 м³ лісу. Скільки буде лісу на цій ділянці через 10 років, якщо його щорічний приріст складає в середньому 2%?

 

 

 

 

 

 

№ 11. Початкова кількість бактерій в колонії складала 8, а через 2 години після того, як їх розмістили в сприятливе середовище, число збільшилось до 100. Через який період часу можна очікувати колонію в 500 бактерій?

 

 

 

 

 

 

 

№ 12. Чисельність популяції складає 5000, останнім часом вона щорічно зменшувалась на 8%. Коли чисельність популяції досягне 2000, вона почне вимирати. Скільки років залишилось існувати популяції?

 

 

 

 

 

 

 

 

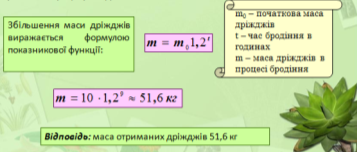
№ 13. Прикладом швидкого розмноження бактерій є виготовлення дріжджів, під час якого по мірі росту бактерій проводиться відповідне додавання цукрової маси. Знайти масу дріжджів, якщо початкова маса складає 10 кг, а тривалість процесу 9 год.

 

 

 

 

 

 

 

№ 14. Відомо, що відношення між вуглеводом С¹² і його радіоактивним ізотопом С¹⁴ в живому організмі постійне. Період напіврозпаду вуглеводуС¹⁴ складає 5760 років. Визначте вік залишків мамонта, знайдених у вічній мерзлоті на Таймирі, якщо відносний склад в них ізотопа С¹⁴ складає 26% від його кількості в живому організмі.

 

 

 

 

 

№ 15. Чому дорівнює маса йоду в кінці 4 діб з початку спостереження, якщо в початковий момент його маса складала 1 г.

 

 

 

 

 

 

 

 

 

 

№ 16. Перший міжнародний еталон радію був виготовлений Марією Кюрі в серпні 1911 року, і складав 16,74 мг чистого радію. Яка кількість радію міститься в еталоні 1991 року?

 

 

 

 

 

 

 

 

 

 

 

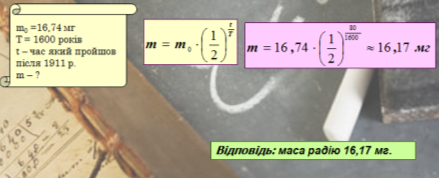
№ 17. Збільшення діаметра об’єктива телескопа дозволяє бачити кількість зірок, які не можна розрізнити простим оком. При цьому гранична «зіркова величина» зірок, які можна побачити через телескоп, обчислюється за формулою , де - діаметр об’єктива телескопа в см.

 

 

 

 

 

 

№ 18. Обчисліть  розчину соляної кислоти, якщо с=0,003 моль/г.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

№ 19. На скільки градусів треба підвищити температуру для прискорення хімічної реакції в 5900 раз, якщо швидкість реакції зростає в геометричній прогресії зі знаменником, що дорівнює 3 при підвищенні температури на кожні 10⁰.

 

 

 

 

 

Похіднафункції: історія зародження та застосування у різних галузях

 

Англія, 1666 рік. І.Ньютон, якому лише 23 роки, робить прорив у математиці – відкриває похідну. І все. Життя Європи полетіло так швидко, що вчені не могли навіть уявити такого.

Розвиток науково-технічного прогресу, війни, виготовлення зброї, епідемії і відкриття цілющого пеніциліну, запуск космічної ракети і створення ядерних реакторів – основою цього всього послужило диференціальне числення. Від високих досягнень до стрімких падінь крокувала поряд похідна, кидаючи свої максимуми і мінімуми¸ похідна, яка миттєво змінила світ.

Похідна – одне з фундаментальних понять математики. Це поняття виникло в XVIIст. у зв'язку з необхідністю розв'язання багатьох задач з фізики, механіки і математики, у першу чергу наступних двох:

•              визначення швидкості прямолінійного нерівномірного руху;
•              побудови дотичної до похідної плоскої кривої.

Математиків ХV– XVIIст. довго хвилювало питання  загального методу для побудови дотичної в будь-якій точці кривої.Та деякі способи її побудови уже були відомі раніше.

•                Давньогрецькийвчений ЕВКЛІД є для нас автором "Начал", по яких навчились математики всього світу. У своїх працях він показав спосіб побудови дотичної до кола.
•                Давньогрецький вчений АРХІМЕД (287 до н.е. - 212 до н.е.) побудував дотичну до спіралі, що носить його ім'я.
•                АПОЛЛОНІЙ (260— 170 до н.е.) – до еліпса, гіперболи та параболи.
•                Французький математик П'ЄР ФЕРМА у 1629 році запропонував знаходження найбільших і найменших значень функцій, що фактично спиралися на застосування похідних.
•                Незалежно від НЬЮТОНА ЛЕЙБНІЦ створив диференціальне й інтегральне числення. Збільшення абсциси він позначав через dx, що відповідає збільшенню ординати – через dy, а похідну - диференціальним коефіцієнтом .
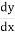•                ЛАГРАНЖ ввів термін «похідна» у 1797р. Сучасні позначення похідної він ввів у вигляді у′ та f′.

Похідна, як і будь-яке інше математичне поняття, має свою історію. Вона виникла з практичних потреб людини і широко використовується у багатьох галузях наук.

 

 

МАТЕМАТИКА

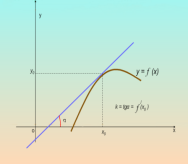Кутовий коефіцієнт дотичної, проведеної до графіка функції в точці з абсцисою х_0, дорівнює похідній в точці х₀,

.

•                 Схема написання рівняння дотичної до графіка функції

	Рівняння дотичної до графіка функції в точці , яка належить графіку.
Скласти рівняння дотичної до графіка функції в точці з абсцисою
Розв’язання	а) f(x)=,  х0=3
Обчислити значення функції в точці	f(х0)=f(3)=3
Знайти похідну функції	f´(x)=
Обчислити значення похідної в точці	f´(х0)= =5
Значення підставляємо в рівняння дотичної	; у =5(х-3)3 = 5х18.

Розв’язання

Відповідь: 1

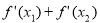•                 На малюнку зображений графік функції у =f(x) та дотичні до нього в точка х₁ та х₂. Користуючись графіком, знайдіть

 

 

 

 

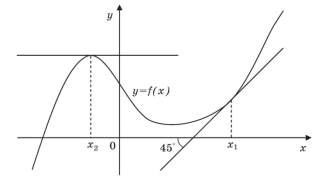
•                 Знайти кут, який утворює з додатнім напрямком осі Ох дотична до графіка функції у = у точці з абсцисою х₀=1.

Розв’язання Отже,

Відповідь:

 

Умова паралельності прямих: y1=k1x+b1, y2=k2x+b2<=>k1=k2, <=> y1y2

Умова перпендикулярності прямих: y1=k1x+b1, y2=k2x+b2 <=> k1k2=1, <=> y1y2.

•                 На графіку функції f(x)= 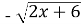знайдіть точку, дотична в якій перпендикулярна до прямої у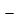4х+5=0.

Розв’язання Умова перпендикулярності прямих: k1k2=1. Виражаємо у і знаходимо k1: у = 4х5; k1=4, тоді k2=. Похідна функції у´=k2. Тоді . Звідси  2х + 6 =16 і х =5. Підставивши значення х=5 у рівняння прямої у = 4х5 знайдемо у =  =. Точка А(5;

Відповідь: А(5;

•             Довести, що 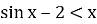 для всіх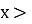 0.

 

Розв’язання Розглянемофункціюf(х). f'(х) для всіх . Тоді якщо 0, то  f(х)тобто

для всіх 0.

•        Поняття похідної можна використовувати під час наближених обчислень, коли провести такі міркування: Нехай, наприклад, треба обчислити наближене значення функції  f(х) 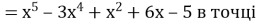х₀= 2, 05.

Розв’язання Значення f у близькій до 2,05 точці х0=2 знаходимо легко f(2)=5. Графік f в околі точки 2 близький до дотичної до нього. Тому, за допомогою формули   f(х) f(х0) + f(х0) можна обчислити значення функції. Маємоf′(х) і f′(х). Отже, f(2) .

З формули f(х) f(х0) + f(х0) можна вивести наближені формули:   та

 

•        Розв’яжіть рівняння 3^х+3^2-х=3(1+cos2)

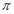
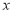Оскільки у нас немає формул, які б дозволяли перетворювати одночасно і показникові, і тригонометричні вирази, то спробуємо розв’язати задане рівняння, використовуючи властивості відповідних функцій, зокрема, спробуємо оцінити область значень функцій, які стоять у лівій і правій частинах рівняння. Для функції, яка стоїть у правій частині рівняння, це легко зробити і без похідної, а для дослідження функції, що стоїть у лівій частині рівняння, зручно використати похідну.

ОДЗ заданого рівняння – усі дійсні числа R. Оцінимо ліву і праву частини рівняння. Оскільки cos2х набуває всіх значень від (-1) до 1, то 1+cos2х набуває всіх значень від 0 до 2. Тоді функція g(x)=3(1+cos2х) набуває всіх значень від 0 до 6. Отже, .

Функцію дослідимо за допомогою похідної.. існує на всій області визначення функції.

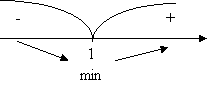
(х)=0; . Оскільки 0, то ; ; 2x-2=0, х=1- критична точка. Відмічаємо критичну точку на області визначення і заходимо знак похідної в кожному проміжку.

Неперервна функція має тільки одну критичну точку, і це точка мінімуму (у ній похідна змінює знак з мінуса на плюс). Тоді в цій точці функція набуває свого найменшого значення: f(x)=6. Отже, f(x)6.

Враховуючи, що g(x), одержуємо, що задане рівняння f(x)=g(x) рівносильне системі . Але значення 6 функція f(x) набуває тільки при х=1, що задовольняє і другому рівнянню системи (g(1)=3(1+cos2)=6. Отже, одержана система (а значить, і задане рівняння) має єдиний розв’язок х=1.

Відповідь: 1.

 

ФІЗИКА

Задача на знаходження миттєвої швидкості нерівномірного руху за відомоюзалежністю координати s від часу розв'язується так:

•              (t)= s^/(t)  -   похідною від координати є швидкість;
•              a(t)=^/ (t)= s ^//(t)  -  похідна від швидкості за часом є прискорення.

Таким чином, прискорення - друга похідна від координати за часом. 

Найбільш характерні задачі з фізики, які розв’язуються за допомогою похідної:

•              знаходження швидкості та прискорення прямолінійного руху тіла чи матеріальної точки;
•              знаходження кутової швидкості тіла обертання;
•              знаходження швидкості зростання маси кристалів;
•              визначенняшвидкості зміни температури під час нагрівання;
•              визначення освітленості електричної лампочки.

Розглянемо способи розв’язування деяких задач.

•                 Матеріальна точка рухається за законом 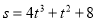(s виміряється у метрах, t — в секундах). Знайти швидкість та прискорення в момент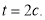

Розв’язання               — швидкість руху точки  в будь-який момент t.               (м/с)— швидкість руху точки в момент               — прискорення руху точки в момент t.               (м/с2)— прискорення руху точки в момент

Відповідь: 52(м/с); 50(м/с2).

•                 При гальмуванні маховик за t секунд повертається на кут 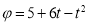(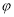— у радіанах). Знайти: кутову швидкість 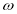обертання маховика в момент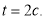; момент часу 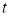, коли обертання скінчиться.

Розв'язання               Кутовою швидкістю називається швидкість зміни кута за час . Кутова швидкість є похідною від кута повороту за часом .               (рад/с)— кутова швидкість в момент               В момент зупинки маховика: Наприкінці третьої секунди кутова швидкість дорівнюватиме нулю, і обертання скінчиться.

Відповідь: =2рад/с;

•                 Кількість тепла Q, потрібного для нагрівання1кг води від 0 до визначається за формулою Q(t)=t +0,0005t² + 0,000006t³. Обчисліть теплоємність води для t = 20.

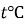
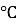
Розв'язання               Теплоємність є похідною від кількості тепла за температурою.  С(t)= Q'(t)= 1+0,0001t + 0,000018t2               C(20)=1+0,00120+0,000018400=1+0,02+0,0072 =1,0272(Дж)

Відповідь:

•                 Матеріальна точка рухається за законом S(t)=2t²+7t. ( S вимірюєтьсяу метрах, t – в секундах). Знайти час t (у секундах), при якому миттєва швидкість матеріальної точки дорівнює 60 м/с.

Розв'язання v = S'(t) = 4t +7 – швидкість руху точки в будь-який момент t.    4t +7 = 60.  Звідси  4t = 53;  t =13, 25с.

Відповідь: 13, 25с.

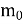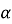
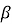
•                 Тіло масою рухається прямолінійно за законом S(t) =t² +t +λ. Довести, що сила, яка діє на тіло є стала.

Доведення F=a a(t)=V'(t)=S''(t);S'(t)=(αt2+ βt+ λ)'=2αt+β;      a(t)=S''(t)=(2αt+ β)'=2α; a(t)=2α, α=const;

Відповідь: Отже, сила, що діє на тіло – стала

 

Похідна функції: прикладні задачі

 

№ 1. Визначити висоту басейну із квадратним дном, об’єм якого 32м³, такого, щоб на облицювання його стін і дна, витрати на матеріали були найменшими.

Розв’язання

Нехай довжина та ширина басейну – .Складемо функцію, за якою можна обчислити площу стін і дна S(х) = + 4х = + .  Дослідимоїї на екстремум:S'(х) = 2х - . S'(х)=0, тоді =0 і х =4.

Відповідь: 4м

№ 2. Задача - проблема «Яку з чашок вигідніше купляти?». Звісно дешевшою є та, на яку іде менше матеріалу. Для цього дослідимо чашки циліндричної форми.

Математично задача звучить так: який із циліндрів з периметром осьового перерізу Р має найбільшу бічну поверхню?

Отже, найбільшу бічну поверхню має циліндр, у якого осьовий переріз – квадрат.

 

№ 3. Перш ніж запропонувати задачу для розв’язування, послухайте таку легенду «У 825 році до н.е. фінікійська царівна Дідона з невеликим військом вибрала зручне місце на північному узбережжі Тунійської затоки. Король Нумібії Ярб погодився продати їй ділянку землі, обмежену «шкурою бика». Дідона не розгубилася. Вона розрізала шкуру на тоненькі смужки, якими обміряла територію найбільшої площі. Так було засновано Карфаген». Якщо ця територія - прямокутник, то які його розміри?

 

№ 4. Швидкість v тіла, що рухається у вертикальному напрямку, змінюється за законом v= 9 - 10t (м/с). Визначити швидкість тіла в момент приземлення, якщо воно в початковий момент знаходилось на висоті 2 м від землі.

Розв’язання

1.               Знайдемо прискорення тіла, що рухається за даним законом

a = v^/ ( t) = - 10 ( м/с² );

Оскільки прискорення стале, то тіло рухається за квадратичним законом:

 h = .

2) v₀ = v(0) =9-10 х 0 = 9 (м/с )

3) Підставимо у формулу  а  та  v₀

h =

Розв’язавши квадратне рівняння, одержимо час приземлення тіла t= 2с та швидкість в момент приземлення v = 9- 10 х 2 = - 11 (м/с )

 

№ 5. Посудина з вертикальною стінкою і висотою h стоїть на горизонтальній площині. На якій глибині треба розмісти отвір, щоб дальність вильоту води з отвору була найбільшою ( швидкість рідини, що витікає, за законом Торрічеллі дорівнює , де x - глибина розміщення отвору, g - прискорення вільного падіння)?

 

 

 

 

 

 

 

 

 

 

 

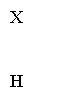
Розв’язання

Позначимо через H відстань отвору в посудині від горизонтальної площини, а через L –відстань точки А від стінки посудини. Тоді L= vt, де t – час польоту води від отвору до площини (в точку А).

З курсу фізики відомо, що

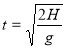         або        .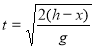

Тоді

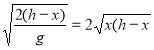,     0 x h.

Знайдемо похідну L’(x) = .

Розв’язуючи рівняння , знаходимо стаціонарну точку .

Оскільки це єдина стаціонарна точка, то вона й буде шуканою.

 

№ 6. Вартість (за годину) утримання баржі складається з двох частин: вартості палива, яка пропорційна кубу швидкості баржі, і вартості амортизації баржі (заробітна плата команди, обладнання та ін.). Загальна вартість утримання баржі за годину, таким чином, виразиться формулою , де v – швидкість судна в км/год; a і b – коефіцієнти, задані для кожного судна. Визначити, при якому v загальна сума утримання на 1 км шляху буде найменшою, якщо a = 0,005, b = 40.             

Розв’язання

. За умовою a = 0,005, b = 40, тоді .

1 км шляху баржа пройде за год. За цей час витрати складуть

 

, (0;).

Треба знайти найменше значення функції на проміжку (0;).

; , якщо 0,01v-=0; 0,01v³= 40; v³=4000;

v= 10 . Оскільки,, безперервна на проміжку (0;) і v= 10 одна стаціонарна точка, то вона є точкою мінімуму, бо

. v= 10 =101,6=16 (км/год).

Відповідь: 16 км/год

 

№ 7. Об’єм продукції u, яку виробляє бригада робітників, описується рівнянням (од.), , де t – робочий час в годинах. Обчислити продуктивність праці, швидкість і темп її зміни через час після початку роботи і за час до її закінчення.

Розв’язання

Продуктивність праці виражається похідною

(од./год.), а швидкість і темп зміни продуктивності – відповідно похідною і похідною логарифмічної функції        = -5t + 15 (од./год ²),

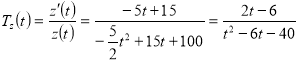( од./год.)

У задані моменти часу і відповідно маємо:

z(1)=112,5 (од/год), z^/(1)=10(од./год²), T(1)=0,09 (од./год) і

z(7)=82,5 (од./год.), z^/(7)=-20(од./год²), T(7)=-0,24 (од/год).

Таким чином, до кінця роботи продуктивність праці суттєво знижується, при цьому зміна знаку z^/(t) і T(t) з плюса на мінус свідчить про те, що збільшення продуктивності праці у першу годину робочого дня змінюється її пониженням в останню годину.

 

№ 8. Дано прямокутний лист жерсті розміром 80 х 50 см. Треба виготовити з нього відкриту зверху коробку найбільшої місткості, вирізавши по кутах квадрати і загнувши краї. Якою повинна бути довжина сторони такого квадрата?

Розв’язання

Позначимо через х довжину сторони квадрата, що вирізується. Очевидно, що 0х25. Об’єм коробки (прямокутного паралелепіпеда) дорівнює добутку площі основи на висоту. При зазначеному способі виготовлення коробки основа її - прямокутник із сторонами 80-2х і 50 – 2х, а висота х; відповідно об’єм коробки становить: V(x)=(80-2x) (50-2x) x=4x³-260x²+ 4000x

 

Задача звелась до знаходження найбільшого значення функції на проміжку [0;25] Знайдемо критичні точки ==12х²-520х + 4000.

12х²-520х + 4000=0; х= і х=10. Інших критичних точок функція не має, бо похідна існує для всіх х.

Проміжку [ 0;25] належить лише одна точка х=10. Обчислимо значення V(x) у цій точці і на кінцях проміжку:

V(10)=410³-26010²+4000=1800; V(0)=0;V(25)=425³-26025²+400025=0

Отже, найбільшого значення функція V(x) досягає на проміжку [0;25] у точці 10. Це означає, що коробку найбільшого об’єму можна виготовити, вирізавши по кутах даного листа жерсті квадрати із стороною 10 см.

 

№ 9. Приставлена до вертикальної стіни драбина довжиною 5 м падає, ковзаючи верхнім кінцем по стіні, а нижнім по поверхні підлоги. З якою швидкістю і прискоренням опускається верхній кінець драбини в момент часу t с, якщо нижній кінець відсувається від стіни зі сталою швидкістю 2 м/с.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

№ 10. Ширина будинку 6 м, а довжина – 9 м, висота фронтону – 4,4 м. Господарю треба побудувати мансарду, поперечний переріз якої має найбільшу площу.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

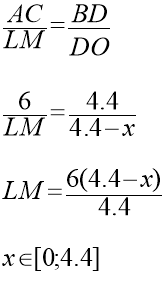
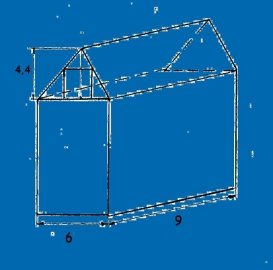
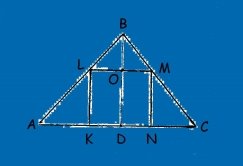
Тоді S=

F(x)=S-шукана функція, яку необхідно дослідити на найбільше значення.

 

 

 

 

 

 

 

 

 

 

 

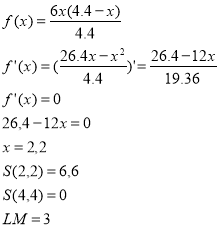
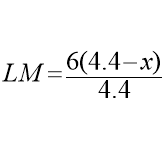
Відповідь: 6,6 м²

Найбільша площа в нас дорівнює 6,6 м² .

Робимо висновок:

   Щоб раціонально використати житлову площу треба зробити мансарду, площа поперечного перерізу якої б дорівнювала 6,6 м². При цьому ширина кімнати дорівнюватиме 3 м. а висота – 2,2 м.

 

№ 11. Витрати на паливо, що необхідне для руху океанського танкера, пропорційне кубу його швидкості та складає 20 у.о. за годину за швидкості 10 вузлів (1 вузол = 1 морська миля за годину; 1 морська миля – 1852 м), а всі інші витрати складають 100 у.о. за годину. Знайдіть найменшу економічну швидкість руху за тихої погоди, якщо відстань до порту призначення 1000 морських миль.

Нехай x - шукана економічна швидкість.

t - час, витрачений на рейс.

Тоді на проходження шляху в 1000 морських миль з економічною швидкостю складає 1000/x год. Витрати на паливо за час проходження усього шляху складає Р₁=kx³*t у.о. Витрати на утримання команди залежить від часу, який танкер затратить на проходження усього шляху і складає 100*t у.о. Знаючи, що час - це відношення пройденого шляху до швидкості, то при економічній швидкості ці затрати становлять 100*1000/x у.о. Загальні витрати становлять: P=Р₁+Р₂, де Р₁ - витрати на паливо; Р₂ - витрати на утримання команди.

• P=kx³*t+100*1000/x=kx^3*1000/x+100*1000/x=1000(kx³+100)/x;
• P=1000(kx3+100)/x – шукана функція
• Маючи рівняння, знайдемо економічну швидкість:
• P=1000(0.02x³+100)/x
• ОДЗ:x ≠ 0
• Знайдемо похідну:
• P’=(1000(0.02x³+100)/x)’=((20x³+100000)/x)’=((20x³+100000)’x –
• - 20x³+100000)x’)/x²=(60x³-20x³-100000)/x²=(40x³-100000)/x²
• Прирівняємо похідну функції до 0:
• (40x³-100000)/x²=0; x ≠ 0 - виходить, що танкер стоїть.
• 40х³ - 100000 = 0
• 40х³ = 100000
• х³ =2500
• х = 13,57 – єдина критична точка функції
• Знайдемо значення функції в цій точці і в околі цієї точки
• P(13,57)=1000(0.02*13.57³+100)/13.57=11050 (у.о.)
• Підставивши значення х=13;х=14, матимемо:
•  Р(13)=11072 у.о.

 Р(14)=11063 у.о.

 

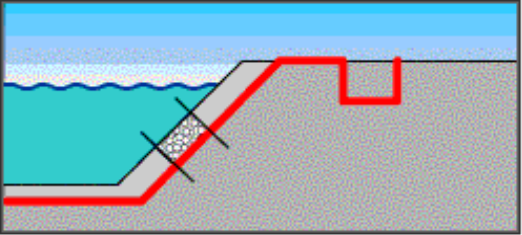№ 12. При якому куті нахилу бічних сторін до більшої основи переріз зрошувального каналу буде мати максимальну площу.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Дослідимо одержану функцію на інтервалі

 

 

Знайдемо похідну функції

 

Знайдемо критичні точки

 

 

 

 

 

 

 

 

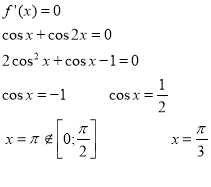
Знаходимо значення функції в точках

 

 

 

 

 

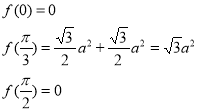
Очевидно, що найбільшого значення функція набуває в точці

Отже, для того, щоб максимально використати місткість побудованого каналу необхідно бічні плити споруди розмістити під кутом      до поверхні каналу.

 

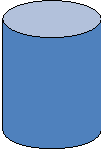№ 13. Визначити розміри циліндричної закритої консервної банки, об’єм якої V см³, щоб її повна поверхня була найменшою, тобто витрати жерсті на її виготовлення були найменшими.

1.Створюємо математичну модель.

Функція, яка досліджуєтся:  f(x) = S п.п. = 2 ПR (h+R)        V = ПR²h => h= V/ПR²    R = x f(x) = 2Пx (x + V/ПR²) – шукана функція.

2. Досліджуємо одержану функцію на найменше значення:

   f’(x) = 4Пx – 2V/x²

   Знаходимо критичні точки:

   4Пx – 2V/x² = 0,   x = ³ V/2П

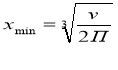3. Оскільки для даної функції існує тільки одна

точка                            , то найменшого значення функція набуває саме в цій точці.

4. З’ясуємо висоту цієї банки при:

 

 

 

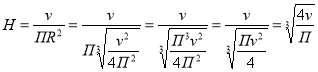
5. Одержали, що H=2R

Отже, щоб витрати жерсті були мінімальними необхідно, щоб висота циліндричної банки дорівнювала її діаметру.

Первісна та інтеграл: історія зародження та застосування у різних галузях

 

Інтеграл виник з парктичної потреби знаходити площі неплоских фігур. Найбільший внесок у вивченні інтегрального числення вніс Архімед.

Одного разу, прийшовши із рибалки, Архімед захотів визначити найбільш точно площу поверхні риби.

Розбивши поверхню риби на прямокутники, він знайшов їх площі, причому чим більшою була кількість прямокутників, тим точнішим було значення площі.

 

 

 

 

 

 

 

 

 

 

Поняття інтеграла пронизує всю сучасну математику. І не тільки це – в науках фізичного і технічного циклів знаходять застосування різні варіації інтеграла. Варто розкрити будь-яку книгу, що відноситься до точних наук, як зустрінеться знак інтеграла і пропозиції, включаючи слово «інтеграл». Більш того, останнім часом увійшли до ужитку такі терміни, як, наприклад, «інтегральна схема», «економічна інтеграція», які прямого відношення до інтеграла не мають, але смислове навантаження зберігають і знаходять широке розповсюдження в літературі і розмовній мові.

Поняття інтеграла та інтегральне числення виникли з потреби обчислювати площі (квадратуру) будь-яких фігур і об'єми (кубатуру) довільних тіл. Передісторія інтегрального числення сходить до старовини.

Евдокс Кнідський (бл. 408-355 рр. до н. е.) - старогрецький вчений. Дав повний доказ теореми про об'єм піраміди; теореми про те, що площі двох кіл відносяться як квадрати їх радіусів. При доведенні він застосував так званий метод «вичерпання», який знайшов своє використання (з деякими змінами) у працях його послідовників. Через дві тисячі років метод «вичерпання» був перетворений у метод інтегрування, за допомогою якого вдалося об'єднати різні завдання - обчислення площі, об'єму, маси, роботи, тиску, електричного заряду, світлового потоку і багато, багато інших.

Проілюструємо «метод вичерпування» на простому прикладі. Припустимо, що нам треба знайти об'єм лимона, який має неправильну форму, і тому застосувати будь-яку відому формулу об'єму не можна. За допомогою зважування знайти об'єм також важко, оскільки щільність лимона в різних частинах його різна. Поступимо таким чином. Розріжемо лимон на тонкі часточки. Кожну часточку приблизно можна вважати циліндриком, радіус основи, якого можна виміряти. Об'єм такого циліндра вирахувати легко за готовою формулою. Склавши об'єми маленьких циліндрів, ми отримаємо наближене значення об'єму всього лимона. Наближення буде тим точніше, чим на більш тонкі частини ми зможемо розрізати лимон.

Слідом за Евдоксом метод «вичерпання» і його варіанти для обчислення об'ємів і площ застосовував стародавній вчений Архімед. Успішно розвиваючи ідеї своїх попередників, він визначив довжину кола, площа круга, об'єм і поверхню кулі. Він показав, що визначення об'ємів кулі, еліпсоїда, гіперболоїда і параболоїда обертання зводиться до визначення об'єму циліндра. Висловлюючись сучасною мовою, Архімед визначив інтеграли.

Термін «інтеграл» (від лат. integer - цілий, тобто ціла, вся - площа) був запропонований у 1696 р. Іоганном Бернуллі.

Ще більш чітко поняття визначеного інтеграла виступає в працях Б. Паскаля. Він вперше познайомився з неподільними у Кавальєрі, про який відгукувався з великою похвалою. Однак, незважаючи на те, що Паскаль користувався терміном "неподільні", він їх розуміє не так, як Кавальєрі. "Сума ординат" для Паскаля - це вже не всі лінії, а сума необмеженого числа прямокутників, сторонами кожного з яких служили ордината і маленькі рівні відрізки абсцис.

У XVII ст. велика група математиків займалася наступними основними завданнями: проведенням дотичної до кривої, що привело до виникнення диференціального числення, і обчисленням квадратури, що спричинило виникнення інтегрального числення. Заслуга Ньютона і Лейбніца полягала у відшуканні внутрішнього зв'язку між цими завданнями, синтез яких і був основою для створення могутнього знаряддя науки і наукового природознавства. Користування теоремою про взаємну оберненість операцій диференціювання і інтегрування і знання похідних багатьох функцій дали Ньютону можливість по флюксіях отримувати флюенти (функції), тобто інтегрувати. Якщо інтеграли безпосередньо не обчислювалися, Ньютон розкладав підінтегральну функцію в степеневий ряд і інтегрував його почленно. Введення такого прийому – заслуга Ньютона. Для розкладання функцій в ряди він найчастіше користувався відкритим ним розкладанням степеня бінома, діленням чисельника на знаменник, знаходження кореня.

Викликає інтерес розробка Лейбніцем символіки диференціального і інтегрального числень. Інтеграл Лейбніц розумів як суму нескінченного числа доданків – визначений інтеграл. У одному з рукописів є запис. Це означає, що взаємна оберненість дій диференціювання і інтегрування у Лейбніца виступали на оперативному рівні. Лейбніц замість слова «інтеграл» вживав «сума»; термін «інтеграл» ввів І. Бернуллі.

Восени 1675 року Лейбніц сформулював основні понятті диференціального і інтегрального числення. Він дав загальні правила вирішення завдань на квадратуру і дотичні, встановив зв'язок між завданнями диференціювання і інтегрування, ввів символіку обох операцій, що збереглася понині.

Відкриття Ньютона і Лейбніца зробило переворот в математиці. Якщо раніше вона була доступна лише вузькому кругу фахівців, які вирішували кожне окреме завдання придуманими ними методами, то після створення алгоритму диференціального і інтегрального числення, застосовного до широкого круга завдань, математика стала інструментом в руках людей, що займаються різними дослідженнями, але що не володіють достатньо глибокими математичними знаннями.

Після знаменного часу Ньютона і Лейбніца розвиток ідеї інтеграла пішов в двох напрямах: інтеграл, що трактувався як межа деякої суми, певний інтеграл, набував досконалих і всеосяжних форм, знаходив все більше і більше застосування при вирішенні задач самої математики, в якій він склався, механіки, фізики, проник в технічні науки і став інструментом, необхідним у всіх галузях природних наук; інтеграл як сімейство первісних, невизначений інтеграл, своїм розвитком викликав виникнення абсолютно нового розділу аналізу – методів інтегрування функцій, а це у свою чергу було зв'язано з появою функцій, не відомих раніше, – клас інтегрованих функцій весь час поповнювався; найважливіше застосування невизначеного інтеграла відноситься до інтегрування диференціальних рівнянь, складових могутнього апарату багатьох наук.

Творчість Коші і Романа протікало тоді, коли в суспільному житті, природознавстві і математиці відбулися істотні зміни. Зросла роль математики в системі наук. У зв'язку з тим, що вона набула аналітичного характеру, математичні методи проникали не тільки в механіку, з якою математика була в тісному контакті ще в часи Архімеда, але і фізику, техніку і економіку. Аналіз став провідною галуззю знань. Розширилася мережа учбових закладів, що готують фахівців, стало більше університетів, вищих технічних шкіл; професори університетів почали займатися науковими дослідженнями, академіки – викладати в університетах. Збільшилася кількість періодичних наукових виданнь, що надало ширшу можливість публікації робіт, поліпшило інформативність.

Проте знов виникли потреби як усередині математики, так а в інших науках, а також пов'язані з обчисленням деяких первісних труднощів принципового характеру висували на перший план визначений інтеграл. Завдання теорії ймовірності, теорії рядів, інтегрування диференціальних рівнянь, математичної фізики, теорії кінцевих різниць приводили до спеціального вигляду визначених інтегралів, зокрема невласним. Прикладом таких інтегралів служить інтеграл Пуассона. Обчисленням таких інтегралів займалися багато видатних математиків. У Ейлера цим питанням відводяться цілі два томи. Дослідженню спеціальних інтегралів присвятили свої праці Лагранж, Лаплас, Пуассон, Коші.

Таким чином, розвиток математики висував необхідність перегляду концепції інтеграла, і це було виконано Коші.

Невизначений інтеграл Коші ввів як частинний випадок визначеного, при змінній верхній межі. Він довів неперервність такого інтеграла по верхній межі і теорему про те, що похідна його по верхній межі рівна підінтегральній функції. Коші довів також справедливість формули Ньютона - Лейбніца. Він висловив положення, пов'язані з диференціюванням і інтегруванням по параметру.

Здається, зовсім мало часу пройшло після введення Коші визначеного інтеграла, але знову виникають мотиви, що вимушують переглядати, уточнювати це поняття, і знову наполегливо працює розум математиків. І поставити останню крапку про «пригоди» ідеї інтеграла випало Ріману. Тільки не слід думати, що розвиток поняття інтеграла закінчився з роботами Рімана. Його творчістю завершився шлях до інтеграла і почався шлях інтеграла, не менш цікавий і істотний для науки.

Дослідження інтеграла після Рімана не припинилися, а пішли прискореним темпом. Якби перерахувати лише математиків, що зробили значний внесок в теорію інтеграла в другій половині XIX і в XX ст., то це зайняло б багато місця. Інтеграл був, є і буде стрижньовим поняттям в математиці.

Вивчаючи на уроках математики інтеграли, учні часто зацікавляться, чи допомагає інтеграл у практичній діяльності людини?

Відповідь може дати нам знання з інтегрального числення. Знайшли застосування інтеграла в економіці, на картопляному полі, на автомобільних дорогах. Багато з нас знає, що для того, щоб зварити смачну кашу, треба взяти відношення води і крупи 3:1.

Розв’язали задачу про хліб і встановили, що для охолодження хліба до температури 30°С потрібно 1год. 11хв.

Таким чином, щоб картопля родила, щоб порядок був на дорогах, щоб парки і сквери прикрашали наше місто, щоб був хліб і до хліба, потрібно вивчати інтеграл.

Первісна та інтеграл: прикладні задачі

 

Продуктивність праці протягом робочого дня змінюється. Нехай - час, що відраховується від початку робочого дня, тоді продуктивність праці є функцією часу, тобто . Якщо потрібно обчислити обсяг випуску продукції, яку виготовив робітник за проміжок часу, то використовується формула

 

№ 1. Денна продуктивність праці робітника заводу наближено виражається формулою , де - кількість продукції за 1 годину. Знайти обсяг випуску продукції за 1 рік, якщо кількість робочих днів дорівнює 240, а тривалість робочого дня 7 годин.

Розв’язання.

Обсяг випуску продукції протягом робочого дня є визначеним інтегралом у межах від до від функції,що виражає продуктивність праці. Тому

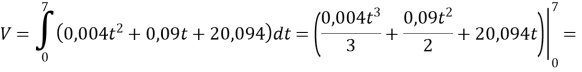
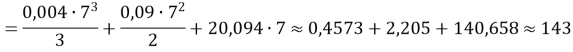
Обсяг випуску продукції за рік складає од.

Відповідь: 34320 од.

 

Кількість товарів, що надходять на склад за одиницю часу, розглядається як функція часу , який відраховується від початку надходження товарів на склад, тобто . Тобто маємо формулу .

 

Якщо -  навантаження на електростанцію кВт·год, де - кількість годин, що відраховується від початку доби, то спожита електроенергія за проміжок часу буде знаходитися за формулою

 

№ 2. Споживання електроенергії, в кВт·год, підприємствами та міським населенням з 8 до 18 годин наближено виражається функцією , де - кількість годин. Обчислити плату за електроенергію, що споживається містом за цей час, якщо тариф – 24,36 коп. за 1 кВт·год.

Розв’язання.

За умовою задачі маємо, що 18-8=10 (годин) місто споживало електроенергію. Тому кількість її за проміжок часу обчислюється за формулою.

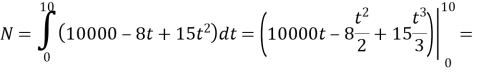
Так, якщо тариф на електроенергію 24,36 коп. за 1 кВт·год, то (коп.) або 25480,56 (грн.) – плата за електроенергію.

Відповідь: 25480,56 грн.

 

Якщо дохід, що поступає щорічно, змінюється в часі і описується функцією і при питомій нормі відсотка, яка дорівнює , відсоток нараховується безперервно. Можна показати, що в цьому випадку дисконтний дохід за час обчислюється за формулою .

 

№ 3. Визначити дисконтний дохід за три роки при процентній ставці 8%, якщо базові капіталовкладення склали 10 млн. грн., і намічається щорічно збільшувати капіталовкладення на 1 млн. грн.

Розв’язання.

Очевидно, що капіталовкладення задаються функцією . Тоді дисконтна сума капіталовкладень . Скористаємося методом інтегрування частинами. Нехай , , тоді , _,

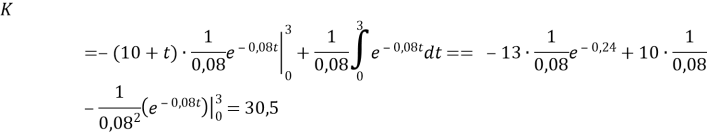
Відповідь: 30,5 млн. грн.

 

Якщо відома функція , яка описує зміну витрат часу на виготовлення виробу в залежності від міри освоєння виробництва, де - порядковий номер виробу в партії. Тоді середній час, який затрачено на виготовлення одного виробу в період освоєння від до виробів, обчислюється за теоремою про середнє: .

Що стосується функції зміни витрат часу на виготовлення виробів , то часто вона має вигляд , де - витрати часу на перший виріб, - показник виробничого процесу.

 

№ 4. Знайти середній час, який затрачено на освоєння одного виробу в період від до виріб, поклавши (хв.), _.

Розв’язання.

Отримаємо (хв.)

Відповідь: 57,2 хв.

 

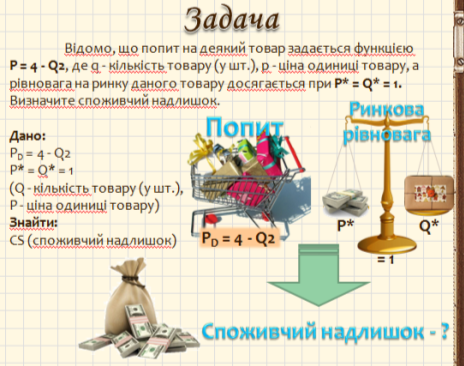
Кожен споживач визначає для себе граничну максимальну суму грошей, яку він міг би заплатити за товар згідно зі своєю оцінкою його граничної корисності. Ця готовність платити є показником сприйняття цінності товару споживачем.

Споживчий надлишок – це різниця між максимальною сумою, яку споживач був готовий заплатити за кількість товару, на яку він пред’являє попит, і фактично заплаченою сумою.

Споживчий надлишок можна порахувати за наступною формулою

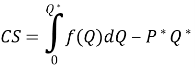
де – споживчий надлишок, – функція попиту, – рівноважна ціна, – рівноважна кількість

 

№ 5.

 

 

 

 

 
. Кросворд «Розв’язування трикутників»

				4	5
1
			2
											7
								6
				3

По горизонталі:

1.Таблиці Брадіса.

2. Теорема, яка дозволяє знайти квадрат будь-якої сторони трикутника.

3. Чим для теореми синусів є рівність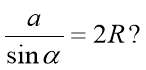

По вертикалі:

4. Трикутник, у якого один із кутів дорівнює 90^о.

5. Теорема, яка використовується при розв’язуванні трикутників, якщо відомо один кут і дві сторони, або одна сторона і два кути.

6. Яка сторона лежить у трикутнику проти більшого кута?

7. У трикутнику проти меншого кута лежить менша…?

Відповіді:

По горизонталі:

1. Чотиризначні. 2. Косинусів. 3. Наслідком.

По вертикалі:

4. Прямокутний.5. Синусів. 6.Більша. 7. Сторона.

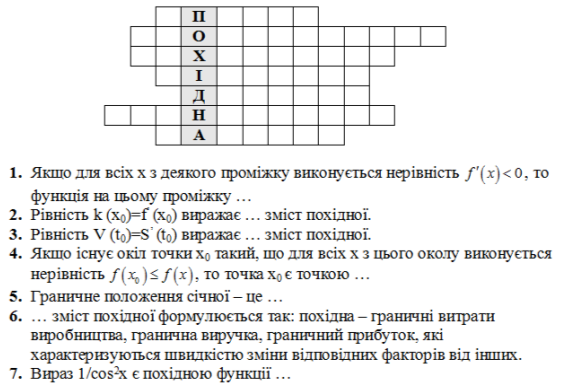Кросворд «Похідна»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пісня «Вивчайте математику!»

 

Так в нас прийнято вважати, що науку цю вивчати

Справа це є зовсім непроста

Та ми хочем Вам сказати: її можна полюбити

Бо у неї є своя краса

Приспів

Синус,   косинус і тангенс, логарифми, похідні

Все що ми би не вивчали - знадобиться у житті

Додаємо, віднімаєм, множим, ділим повсякчас

Математику вивчати закликаєм усіх Вас.

 

А щоб фізику пізнати, математику слід знати

Нам про це відомо вже здавна

Лікарю чи інженеру, програмісту чи банкіру

Кожному потрібна є вона

Список використаних джерел

 

1.         Є.П. Нелін, О.Є. Долгова  Алгебра 11 кл. Академічний рівень. Профільний рівень. Харків «Гімназія» 2011 р.
2.         Алексеев В.М.. Элементарная математика. Киев «Вища школа». 1989.
3.         Богомолов Н.В. Практические занятия по высшей математике. Москва «Высшая школа». 1973.
4.         В.В. Карпік «Відпрацюй навички та перевір себе» Харків «Основа» 2012.
5.         Ю.О.Захарійченко, О.В.Школьний Енциклопедія тестових завдань. Повний курс математики в тестах 5-11 кл. «Ранок» 2011 р.
6.         Задачи по алгебре и началам анализа для 10-11 кл. Москва «Просвещение» 1990.
7.         Литвиненко Г.М., Бурда М.І. Математика. Завдання для  тестової перевірки знань, умінь і навичок випускників ЗОШ, ліцеїв та гімназій. Київ. 1993.
8.         Прохоров А.М.. Большая Советская Энциклопедия. Том 10, изд. 3, Москва (Советская энциклопедия) . 1972.
9.         Роєва Т.Г., Хроленко Н.Ф.. Алгебра в таблицях. Харків «Академія», 2001.
10.    ГП.Бевз, В.Г.Бевз, Н.Г. Владимирова Алгебра «Алгебра и начало анализа» профильный уровень 11 класс. Киев «Освіта» 2011.
11.          Энциклопедический словарь юного математика/Сост. А.П.Савин. – М. : Педагогика, 1989.
12.          Математична хрестоматія. Алгебра і початки аналізу. За ред. М.І.Кованцова. – К.: Радянська школа, 1977.
13.          Виленкин Н.Я. Функции в природе и технике. – М.: Просвещениу, 1978.
14.          Выгодский М.Я. Справочник по элементарной математике. – М.: Государственное издательство физико-математической литературы, 1962.
15.    Алгебра и элементарные функции. 10 класс. В.К. Совайленко, О.В. Лебедева. Ростов на Дону «Феликс», 1998 г.
16.    Процентные вычисления. 10 – 11 классы. «Дрофа», Москва, 2003 г.
17.    Полный курс логарифмов. Естественнонаучный профиль. П.И. Самсонов, Школьная пресса. Москва, 2005 г.
18.    Школьникам о математике и математиках. М.М. Лиман, Просвещение, Москва, 1981 г.