Крамська Ю. І.

СТЕЖИНАМИ МАТЕМАТИКИ

або

про математику після уроків

Ця брошура містить додатковий матеріал, який не вивчається на уроках: цікаві задачі (багато із них з розв’язанням), математичні фокуси, відомості з історії математики.

Мета цього посібника – дати вчителеві матеріал, застосування якого сприяло б підвищенню інтересу учнів до математики, а отже, глибшому її засвоєнню.

Матеріал розподілено за темами,що відповідають запропонованій програмі математичного гуртка для дітей 5-6 класів.

Брошура призначена для вчителів математики та учнів, які мають бажання розширити свої знання.

Зміст

1. Вступ. Теоретичні відомості.
2. Організація роботи математичного гуртка.
3. Матеріали для допомоги у підготовці до занять гуртка.
   1.   Вступне заняття. Історія розвитку математики
   2.          Практичні завдання. Історичні задачі
4. Нестандартні способи рахунку або швидкий рахунок без калькулятора.
   1.   Як виникли числа.
   2.   Диво лічильники.
   3.   Стародавні способи множення.
      • Російський селянський спосіб множення.
      • Метод «грат» або індійський спосіб множення.
      • Множення способом «Маленький замок».
      • Множення на пальцях.
      • Китайський спосіб множення.
      • Італійський спосіб множення.
      • Єгіпетский спосіб множення.
   4.   Таблиця Оконешникова
5. Усний рахунок – гімнастика розуму.
6. Математичні фокуси.
7. Десять цікавих фактів про числа з повсякденного життя.
8. Походження життя.
9. Математичні цікавинки.
10. Магічні квадрати.
11.      Деякі ознаки подільності натуральних чисел, які не вивчаються в школі.
12. Сірникова математика.

Найлегша ноша – це знання. Навчитись – наше завдання. Тож ніколи не лінуйся,

А навчайся і тренуйся!

На сьогодні до числа найбільш актуальних питань освіти є поліпшення якості освіти, зокрема науково-технічної, є необхідною умовою формування інноваційного суспільства та підвищення конкурентоспроможності економіки. В умовах становлення і розвитку високотехнологічного інформаційного суспільства в Україні виникає необхідність підвищення якості та пріоритетності позашкільної науково-технічної освіти.

Іноді можна почути, що математика складна, суха і нецікава наука.

Людей, які люблять математику, це вражає й ображає. Математика сувора, але красива. А завдання вчителя в тому, щоб розкривати перед учнями її емоційний бік, чуйну і вродливу стать. Як краще цього домогтися? Як зацікавити дітей математикою? Як привернути їхню увагу до цього предмету?

В предметах і явищах навколишнього світу існує багато властивостей, зв’язків і відношень, пов’язаних з математикою. Своїм учням я пропоную шукати математику всюди, осмислювати її роль в житті людини. Важливо навчити учнів не лише бачити математику навколо себе, але й використовувати математичні знання у всіх сферах життя

Для пробудження в учнів інтересу до математики важливу роль відіграє позакласна робота, особливо заняття предметного гуртка. Тому важливим напрямком роботи гуртка є знайомство з прикладною математикою.

Створення навчальної програми математичного гуртка

«Незвичайна математика» обумовлено необхідністю розвитку зацікавленості математикою дітей.

М.В.Остроградський.

Кожний учитель прагне, зацікавити учнів предметом, який він викладає, адже це є запорукою успішного навчання.

«Зацікавити розум дитини - ось що є одним з основних положень нашої доктрини, і ми нічим не нехтуємо, щоб прищепити учневі смак, ми сказали, б навіть пристрасть до навчання», - писав видатний український, математик

Одним із засобів зацікавлення учнів математикою є добре продумана позакласна робота. Вона є однією з форм організації пізнавальної діяльності учнів різного віку, але разом з тим вимагає конкретних знань, ерудованості, широкої обізнаності з математичних дисциплін.

Математичні гуртки є основною формою позакласної роботи з математики. Заняття в них доповнюють роботу на уроках і дають можливість задовольнити інтереси та бажання; учнів, що виходять за межі навчальної програми. Тематика занять гуртка повинна відповідати тим знанням, яких набувають учні в процесі навчання, і тому вона пов'язана з програмним» матеріалом. У процесі гурткової роботи учні вчаться розв'язувати математичні проблеми, працювати з математичною літературою тощо.

Як правило, заняття гуртка проводять двічі на місяць.

Ініціатором і організатором гурткової роботи з математики повинен бути вчитель. Він складає план роботи гуртка і координує його діяльність, враховуючи інтереси та вікові особливості учнів.

Плануючи роботу гуртків, слід передбачити розширення практичних навичок і вмінь, якими учні оволодівають у процесі навчання на уроці. Для цього на заняттях учням можна пропонувати практичні роботи з програмних тем математики, ознайомлювати з роботою мікрокалькуляторів і комп'ютерів тощо. Учитель також повинен залучати учнів до самостійної творчої праці.

На засіданнях математичних гуртків можна також готувати учнів до участі в математичних олімпіадах різних рівнів (шкільних, районних, міських, обласних та республіканських).

Слід зауважити, що ефективність роботи гуртка підвищується, якщо основний його склад буде постійним.

Організувавши математичний гурток, слід особливу увагу приділяти тим формам гурткових занять, що дають можливість більшості учнів виявити свою ініціативність і розраховані на активну роботу всіх членів гуртка.

Математика – найстародавніша з усіх наук. Поняття числа одне з основних понять математики виникло з практичних потреб людини на світанку історії суспільства.

Ще в давні часи математику називали «царицею наук», «ключем до всіх наук». Старогрецький філософ Платон (4 ст. до н. е.) вважав математику знаряддям для вивчення філософії і над дверима

«Академії» - будинку, в якому він займався зі своїми учнями, звелів зробити напис: «Нехай сюди не входить ніхто, хто не знає геометрії». А одному з тих, хто бажав стати членом школи, не знаючи геометрії, він сказав: «Іди геть! Ти не маєш знаряддя для вивчення філософії».

Видатні вчені всіх часів надавали математиці великого значення.

«Ніяке людське дослідження не може бути назване істиною, якщо воно не проходить через математичні доведення», - писав видатний італійський художник, учений і інженер Леонрдо да Вінчі ( 1452- 1519).

Видатний італійський фізик, механік і астроном Галілео Галілей (1564-1642) казав, справжню філософію «описано у величезній книзі, яка завжди відкрита нашим очам». Ця книга є Всесвіт, який треба навчитись читати, «написано ж її мовою математики ». «Природа розмовляє мовою математики: букви цієї мови – круги, трикутники та інші математичні фігури».

Велике значення надавав математиці і видатний учений- енциклопедист М. В. Ломоносов (1711-1765). Він писав: «Усе, що без того було темне, сумнівне і неправильне, математика зробила зрозумілим, правильним, очевидним». «Математику вже тому вчити треба, що вона розум до ладу приводить». «Хімія – права рука фізики, математика – її око».

Математика допомагає людині в усіх її справах. Вона потрібна не лише інженерам, конструкторам. Без вимірювань і обчислень не можна зробити й стільця. «Політ – це математика», - казав відомий льотчик В. П. Чкалов.

Без математики не обійтись і художнику: вона потрібна йому, наприклад, щоб будувати перспективу, додержуватись певного масштабу зображення.

У наш час без інформаційних технологій ніхто не уявляє свого життя. Без них неможливий подальший розвиток науки, техніки, економіки. Найпростіші обчислювальні машини було винайдено дуже давно, але лише наприкінці 19 ст. рівень техніки виявився достатнім для налагодження їх фабричного виробництва.

Ставали складнішими наукові і технічні проблеми, ускладнювались математичні формули та рівняння, до яких зводилось їх вирішення, зросла кількість потрібних обчислювальних операцій.

Вдосконалювались і обчислювальні пристрої. Тепер вважається цілком доступною задача, яка потребує ста років роботи обчислювача.

Під час розв’язування задач в 5-6 класах можна широко використовувати давньогрецькі та давньоримські задачі, більшість з яких відрізняються своєю простотою та нестандартним змістом.

Подібних задач існує безліч, що мають різний рівень складності.

Такі задачі зацікавлять школярів нестандартним сюжетом. Основною перевагою використання історичних задач є те, що їх розв’язання вимагає не тільки математичних знань, а й кмітливості, творчості, вміння логічно мислити, бажання знайти нетрадиційні шляхи розв’язання.

Історичні задачі

Задача № 1 До дати прийняття Руссю християнства додати дату загибелі князя, який завжди дотримувався правил лицарської честі - ніколи не нападав зненацька. Це йому належать слова: «Іду на ви». Назвіть подію, яка пов'язана з числом, отриманим у результаті.

Задача № 2 Легенда про винахід шахів. Шахову

гру винайшли в Індії. Індійський принц Сирам, покликав до себе її винахідника, ученого Сету, і сказав : «Я хочу нагородити тебе, за прекрасну гру, яку ти придумав. Я виконаю будь-яке твоє бажання».

«Володарю, — відповів Сета, — накажи видати мені за першу клітинку шахівниці одну пшеничну зернину, за другу — 2 зернини, за третю — 4, і так за кожну клітинку вдвічі більше, ніж за попередню». «Ти одержиш свої зерна. Але твоє прохання не варте моєї щедрості.». «Ми обчислили, — сказали придворні математики, — кількість

зерен. Число це таке велике, що зерен не вистачить ні в яких коморах, навіть цілого царства. Не знайдеться такої кількості зерен і на всьому просторі Землі.». «Напишіть мені це д число» - 18446744073709551615. Маса такої кількості зерен більша за масу пшениці, зібраної людством до теперішнього часу.

Задача № 3 У 2004 р. до н. е. р. купець з Ур відправився з торговельним караваном до Фінікії. Було йому 40 років. Додому він повернувся лише через три роки. За рік до від'їзду у нього народився

син. В якому році народився купець? В якому році народився його син? В якому році купець повернувся додому?

Задача №4 Віслюк і Мул йшли разом навантажені мішками однакової ваги. Віслюк скаржився на важкість ноши. «Чому ти скаржишся, - сказав Мул, - якщо ти мені віддаси один свій мішок, то моя ноша стане вдвічі більшою за твою, а якщо я тобі віддам один свій мішок, то наш вантаж зрівняється». Скільки мішків було у кожного?

Задача №5 В клітці знаходяться деяке число фазанів та кроликів. Відомо, що вся клітка містить 30 голів і 94 ноги. Потрібно дізнатися число фазанів та число кроликів.

Задача №6 Задача Сунь-Цзи (китайський математик ІІІ-ІVст.) Знайти число, яке при діленні на 3 дає остачу 2, при діленні на 5 дає остачу 3 і при діленні на 7 дає остачу 2.

Задача №7 Задача Л. Ейлера (1707-1783)

Деякий чиновник купив коней і биків за 1770 талерів. За кожного коня він сплатив по 31 талеру, а за кожного бика – по 21 талеру. Скільки коней і биків він купив?

Задача №8. У 2 тис. до нашої ери в передмісті Нінелі (Ассірія) сталася пожежа. Власник будинку прибіг, коли вогонь вже сягнув даху. Побачивши сусідів, які хотіли гасити пожежу водою, він закричав:

- Не лийте воду, бо загине моє найголовніше багатство – моя бібліотека!

Чому він так сказав?

(Відповідь: «Книги» ассірійців являли собою глиняні плитки з видавленими на них пісьменами).

Підраховувати предмети люди навчилися ще в древньому кам'яному столітті - палеоліті, десятки тисяч років назад. Як це відбувалося? Спочатку люди лише на око порівнювали різні кількості однакових предметів. Вони могли визначити, в якій з двох куп більше плодів, в якому стаді більше оленів і так далі. Якщо одно плем'я міняло спійманих риб на зроблені

людьми іншого племені кам'яні ножі, не треба було вважати, скільки принесли риб і скільки ножів.

Досить було покласти поряд з кожною рибою по ножу, щоб обмін між племенами відбувся.

Щоб з успіхом займатися сільським господарством, знадобилися арифметичні знання. Без підрахунку днів важко було визначити, коли потрібно засівати поля, коли починати полив, коли чекати потомства від тварин. Потрібно було знати, скільки овець в стаді, скільки мішків зерна лежить в коморі.

І ось більше восьми тисяч років назад древні пастухи стали робити з глини кухлі - по одному на кожну вівцю. Щоб дізнатися, чи не пропала за день хоч одна вівця, пастух відкладав убік по гуртку кожного разу, коли чергова тварина заходила в загороду. І тільки переконавшись, що овець повернулося стільки ж, скільки було гуртків, він спокійно йшов спати. Але в його стаді були не лише вівці - він пас і корів, і кіз, і ослів. Тому припало поділася з глини і інші фігурки. А землероби за допомогою глиняних фігурок вели облік зібраного урожаю, відмічаючи, скільки мішків зерна покладені в комору, скільки глеків олії вичавлені з оливок, скільки виткано шматків льняного полотна. Якщо вівці приносили приплід, пастух додавав до кухлів нові, а якщо частина овець йшла на м'ясо, декілька гуртків доводилося прибирати. Так, ще не уміючи рахувати, займалися древні люди арифметикою.

Потім в людській мові з'явилися числівники, і люди змогли називати число предметів, тварин, днів. Зазвичай таких числівників було мало. Наприклад, у племені річки Муррей в Австралії було два простих числівників: энэа(1) і петчевал(2). Інші числа вони виражали складеними числівниками: 3= "петчевал-энэа", 4 "петчевал-петчевал" і т. д. Ще одно австралійське плем'я - камилороев мало прості числівники малий(1), булан(2), гулиба(3) . І тут інші числа виходили складанням менше: 4= "булан - булан", 5= "булан - гулиба", 6= " гулиба - гулиба" і так далі.

У багатьох народів назва числа залежала від підраховуваних предметів. Якщо жителі островів Фіджі рахували човни, то число 10 називали " боло"; якщо вони рахували кокосові горіхи, то число 10 називали "каро". Так само поступали ті, що живуть на Сахаліні і берегах Амура нивхи. Ще в минулому столітті одно і те ж число вони називали різними словами, якщо рахували людей, риб, човни, мережі, зірки, палиці. Ми і зараз використовуємо різні невизначені числівники зі значенням "багато": "натовп", "стадо", "зграя", "купа", "пучок" і інші.

З розвитком виробництва і торгового обміну люди стали краще розуміти, що загального у трьох човнів і трьох сокир, десяти стріл і десяти горіхів. Племена часто вели обмін "предмет за предмет"; приміром, обмінювали 5 їстівного коріння на 5 риб. Ставало ясно, що 5 одно і те ж і для коріння, і для риб; значить, і називати його можна одним словом.

Поступово люди почали використовувати для рахунку камінчики, палички, частини власного тіла. От як відомий російський учений Н.Н. Миклуха - Маклай описував рахунок папуасів : "Папуас загинає один за іншим пальці руки, причому видає певний звук, наприклад "бе, бе, бе.". Долічивши до п'яти, він говорить: "Ибон-бе"(рука). Потім він загинає пальці іншої руки, знову повторюючи "бе, бе."., поки не дійде до "ибон- али"(дві руки). Потім він йде далі, примовляючи "бе, бе"., поки не дійде до

"самба-бе"(одна нога) і "самба-али"(дві ноги). Якщо треба вважати далі, папуас користується пальцями рук і ніг кого-небудь іншого".

Схожі способи рахунку застосовували і інші народи. Так виникли нумерації, ґрунтовані на рахунку п'ятірками, десятками, двадцятками.

Досі я розповідала про усний рахунок. А як записували числа? Спочатку, ще до виникнення писемності, використали зарубки на палицях, насічки на кістках, вузлики на вірьовках. Знайдена вовча кістка в Дольни – Вестонице (Чехословаччина), мала 55 насічок, зроблених більше 25000 років тому.

Коли з'явилася писемність, з'явилися і цифри для запису чисел.

Спочатку цифри нагадували зарубки на палицях: в Єгипті і Вавілоні, в Этрурии і Фініки, в Індії і Китаї невеликі числа записували паличками або рисками. Наприклад, число 5 записували п'ятьма паличками. Індійці астеки і майя замість паличок використали точки. Потім з'явилися спеціальні знаки для деяких чисел, таких, як 5 і 10 .

У той час майже усі нумерації були не позиційними, а схожими на римську нумерацію. Лише одна вавилонська шестидесятеричная нумерація була позиційною. Але і в ній довго не було нуля, а також коми, що відділяє цілу частину від дробової. Тому одна і та ж цифра могла означати і 1, і 60, і 3600. Вгадувати значення числа доводилося по сенсу завдання

За декілька століть до нової ери винайшли новий спосіб запису чисел, при якому цифрами служили букви звичайного алфавіту. Перші 9 букв означали числа десятки 10, 20,., 90, а ще 9 букв означали сотні. Такою алфавітною нумерацією користувалися до 17 ст. Щоб відрізнити "справжні" букви від чисел, над буквами - числами ставили риску (на Русі ця риска називалася "титло").

У усіх цих нумераціях було дуже важко виконати арифметичні дії. Тому винахід в 6 ст. індійцями десяткової позиційної нумерації по праву вважається одним з найбільших досягнень людства. Індійська нумерація і індійські цифри сталі відомі в Європі від арабів, і зазвичай їх називають арабськими.

При записі дробів ще довгий час цілу частину записували в новій, десятковій нумерації, а дробову - в шестидесятеричной. Але на початку 15 ст. самаркандський математик і астроном аль- Каші став вживати в обчисленнях десяткові дроби.

Числа, з якими ми працюємо - з додатними і від’ємними числами. Але, виявляється, що це не усе числа, які використовують в математиці і інших науках. І дізнатися про них можна не чекаючи старшої школи, а набагато раніше, якщо вивчати історію виникнення чисел в математиці.

Він все розуміє з півслова і тут же формулює висновки, до якого звичайна людина, можливо, прийде шляхом довгих і обтяжливих роздумів. Книги він поглинає з неймовірною швидкістю, а на першому місці в його шорт-листе бестселерів - підручник із цікавої математики. У момент рішення найважчих і незвичайних завдань в його очах горить вогонь натхнення. Прохання сходити в магазин або

помити посуд залишаються без уваги або виконуються з великим невдоволенням. Сама краща нагорода - це похід в лекторій, а найцінніший подарунок - книга. Він максимально практичний і у своїх вчинках в основному

підкоряється розуму і логіці. Він холодно відноситься до людей, що оточують його, і вважатиме за краще катанню на роликах шахову партію з комп'ютером. Будучи дитиною, він не по роках усвідомлює власні недоліки, відрізняється підвищеною емоційною стійкістю і пристосовністю до зовнішніх обставин.

Цей портрет написаний зовсім не з аналітика ЦРУ. Так, на думку психологів, виглядає людина-калькулятор, індивідуум, що має унікальні математичні здібності, що дозволяють йому вмить робити в думці найскладніші підрахунки.

У Ванскому районі західної Грузії живе Арон Чикашвілі. Він швидко і точно робить в думці складні обчислення. Якось друзі вирішили перевірити можливості "чудо-лічильника". Завдання було складним: скільки слів і букв скаже диктор, що коментує другий тайм футбольного матчу "Спартак"(Москва)

- "Динамо"(Тбілісі). Одночасно був включений магнітофон. Відповідь послідувала, як тільки диктор сказав останнє слово: 17427 букв, 1835 слів. На перевірку пішло 5 годин. Відповідь виявилася правильною.

Розповідають, що батько Гауса зазвичай платив своїм робітником у кінці тижня, додаючи до кожного денного заробітку за наднормовий годинник.

Одного разу після того, як Гаус-батько закінчив розрахунки, дитина, що стежила за операціями батька, якій були три роки, вигукнув: " Папа, підрахунок не вірний! Ось така має бути сума". Обчислення повторили і із здивуванням переконалися, що малюк вказав правильну суму.

Цікаво, що багато "чудо-лічильники" не мають поняття взагалі, як вони вважають. " Вважаємо, і все! А як вважаємо, Бог його знає". Деякі "лічильники" були зовсім неосвіченими людьми. Англієць Бакстон, "лічильник-віртуоз", так ніколи і не навчився читати; американський "негр-лічильник" Томас Фаллер помер безграмотним у віці 80-ти років.

Проводилися змагання в інституті кібернетики Української академії наук. У змаганні брали участь молодий "лічильник-феномен" Ігор Шелушков і ЕОМ "Світ". Машина за декілька секунд зробила безліч складних математичних операцій. Переможцем в цьому змаганні вийшов Ігор Шелушков.

Так, багато "лічильників-феноменів" користуються особливими прийомами швидкого рахунку і спеціальними формулами. Значить, ми теж можемо користуватися деякими з цих прийомів.

У Росії 2-3 століття тому серед селян деяких губерній був поширений спосіб, який не вимагав знання усієї таблиці множення. Потрібно було лише уміти множити і ділити на 2. Цей спосіб дістав назву селянського(існує думка, що він бере початок від єгипетського).

Суть його в тому, що множення будь-яких двох чисел зводиться до ряду послідовних ділень одного числа навпіл при одночасному подвоєнь іншого числа.

Приклад: 32 х 13

Таблиця 1.

Ділення навпіл(див. ліву половину Таблиці.1) продовжують до тих пір, поки в частці не вийде 1, паралельно подвоюючи інше число(права частина Таблиці.1). Останнє подвоєне число і дає шуканий результат.

Неважко зрозуміти, на чому цей спосіб ґрунтований: добуток не змінюється, якщо один множник зменшити удвічі, а інший удвічі ж збільшити. Ясно тому, що в результаті багатократного повторення цієї операції виходить шуканий добуток:( 32 х 13 ) = ( 1 х 416 )

Особливо уважні помітять "А як бути з непарними числами, які не кратні

2-м"?.

Так, нехай нам необхідно помножити два числа: 987 і 1998. Одно запишемо ліворуч, а друге - справа на одному рядку. Ліве число ділитимемо на 2, а праве - множити на 2 і результати записувати в стовпчик. Якщо при діленні виникне залишок, то він відкидається.

Операцію продовжуємо, поки ліворуч не залишиться 1. Потім викреслимо ті рядки, в яких

ліворуч стоять парні числа і складемо числа, що залишилися, в правому стовпці. Це і є шуканий твір. Дана графічна ілюстрація по цьому опису. ( див. Таблицю 2.

1) Видатний арабський математик і астроном Абу Абдалах Мухаммед Бен Мусса аль - Хорезми жив і працював у Багдаді. "Аль - Хорезми" буквально означає "з Хорезми", тобто народився в м. Хорезме(зараз входить до складу Узбекистану). Учений працював у Будинку мудрості, де були бібліотека і обсерваторія, тут працювали майже усі великі арабські учені.

Відомостей про життя і діяльність Мухаммеда аль - Хорезми дуже мало. Збереглися лише дві його роботи - по алгебрі і по арифметиці. У останній з цих книг дано чотири правила арифметичних дій, майже такі ж, що використовуються у наш час.

2). У своїй "Книзі про індійський рахунок" учений описав спосіб, придуманий в Древній Індії, а пізніше названий "методом грат"(він же "ревнощі"). Цей метод навіть простіше, ніж вживаний сьогодні.

Множимо, наприклад, числа 6827 і 345:

1.Викреслюємо квадратну сітку і пишемо один з номерів над колонками, а другий по висоті. У запропонованому прикладі можна використати одну з цих сіток.

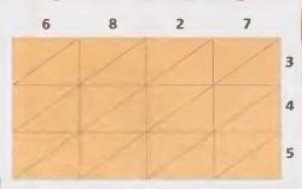
2. Вибравши сітку, множимо число кожного ряду послідовно на числа кожної колонки. В цьому випадку послідовно множимо 3 на 6, на 8, на 2 і на 7. Подивися на цій схемі, як пишеться твір у відповідній клітині.

Сітка 1

3. Подивися, як виглядає сітка з усіма заповненими клітинами.

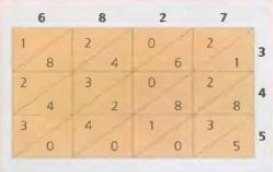Сітка 1

4. На закінчення складаємо числа, наслідуючи діагональні смуги. Якщо сума однієї діагоналі містить десятки, то додаємо їх до наступної діагоналі.

Сітка1

Подивися, як з результатів складання цифр по діагоналях(вони виділені жовтим фоном) складається число 2355315, яке і являється твір чисел 6827 і 345, тобто 6827

х 345 = 2355315.

Цей спосіб носить ще романтичну назву "ревнощі", або

"гратчасте множення".

Спочатку малюється прямокутник, розділений на квадрати, причому розміри сторін прямокутника відповідають числу десяткових знаків у множеного і множника. Потім квадратні клітини, діляться по діагоналі, і ".виходить картинка, схожа на гратчасті віконниці-жалюзі, - пише Пачоли. - Такі віконниці вішалися на вікна венеціанських будинків, заважаючи вуличним перехожим бачити, пані, що сидять у вікон, і черниць".

Мною розглянутий простий приклад, проте, цим способом можна множити будь-які багатозначні числа.

Розглянемо ще один приклад: перемножимо 987 і

12:

• малюємо прямокутник 3 на 2(по кількості десяткових знаків у кожного множника);
• потім квадратні клітини ділимо по діагоналі;
• вверху таблиці записуємо число 987;
• ліворуч таблиці число 12(див. малюнок);
• тепер в кожен квадратик впишемо твір цифр - співмножників, розташованих в одному рядку і в одному стовпці з цим квадратиком, десятки вище за діагональ, одиницю нижче;
• після заповнення усіх трикутників, цифри в них складають уздовж кожної діагоналі;
• результат записуємо справа і внизу таблиці(див. малюнок);

987 ∙ 12=11844

Цей алгоритмом множення двох натуральних чисел був поширений в середні віки на Сході і Італії.

Незручність цього способу ми відмітили в трудомісткості підготовки прямокутної таблиці, хоча сам процес обчислення цікавий і заповнення таблиці нагадує гру.

Множення чисел зараз вивчають в першому класі школи. А ось в середні віки зовсім небагато володіли мистецтвом множення. Рідкісний аристократ міг похвалитися знанням таблиці множення, навіть якщо він закінчив європейський університет.

За тисячоліття розвитку математики було придумано безліч способів множення чисел. Італійський математик Лука Пачоли у своєму трактаті "Сума знань по арифметиці, стосункам і пропорціональності"(1494 р.) приводить вісім різних методів множення. Перший з них носить назву "Маленький замок".

Перевага способу множення "Маленький замок" в тому, що вже із самого початку визначаються

цифри старших  розрядів, а це буває важливо, якщо вимагається швидко оцінити величину.

Цифри верхнього числа, починаючи із старшого розряду,  по черзі множаться на нижнє число і записуються в стовпчик з додаванням потрібного числа нулів. Потім результати складаються.

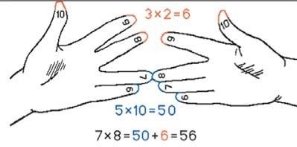Староруський спосіб множення на пальцях є одним з найбільш споживаних методів, яким успішно користувалися упродовж багатьох століть російські купці. Вони навчилися множити на пальцях однозначні числа від 6 до 9. При цьому досить було володіти початковими навичками пальцьового рахунку "одиницями", "парами", "трійками", "четвірками", "п'ятірками" і "десятками". Пальці рук тут служили допоміжним обчислювальним пристроєм.

Для цього на одній руці витягали стільки пальців, на скільки перший множник перевершує число 5, а на другій робили те ж саме для другого множника. Інші пальці загинали.

Потім бралося число(сумарне) витягнутих пальців і множилося на 10, далі перемножувалися числа

Наприклад, помножимо 7 на 8. У розглянутому прикладі буде загнуто 2 і 3 пальці. Якщо              скласти кількості загнутих пальців(2+3=5) і перемножити кількості не загнутих(2-3=6), то вийдуть              відповідно числа десятків і одиниць шуканого твору  56 . Так можна обчислювати              твір будь-яких однозначних чисел, більше 5.

Множення для числа 9 : 9-1, 9-2 ... 9-10 - легше вивітрюється з пам'яті і важче перераховується вручну методом складання, проте саме для числа 9 множення легко відтворюється "на пальцях". Розчепірте пальці на обох руках і

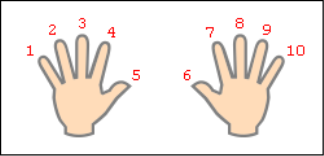поверніть руки долонями від себе. Подумки присвойте пальцям послідовно числа від 1 до 10, починаючи з мізинця лівої руки і закінчуючи мізинцем правої руки(це зображено на малюнку).

Припустимо, хочемо помножити 9 на 6. Загинаємо палець з номером,

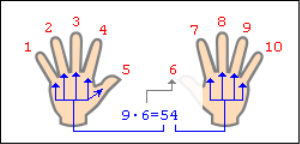
рівним числу, на яке ми множитимемо дев'ятку. У нашому прикладі треба загнути палець з номером 6. Кількість пальців зліва від загнутого пальця показує нам кількість десятків у відповіді, кількість пальців справа - кількість одиниць. Ліворуч у нас 5 пальців не загнуті, справа - 4 пальці. Таким чином, 9- 6=54. Нижче на малюнку детально показаний увесь принцип "обчислення".

Ще приклад: треба вичислити 9-8=?. По ходу справи скажемо, що в якості "рахункової машинки" не обов'язково можуть виступати пальці рук. Візьміть, приміром, 10 клітинок в зошиті. Закреслюємо 8-у клітинку. Ліворуч залишилося 7 клітинок, справа - 2 клітинки. Означає 9-8=72. Все дуже просто.

7 клітинок 2

клітинки

І так, правила рахунку :

Один загнутий палець - це число 6, два пальці - 7, три пальці - число 8, чотири пальці - число 9.

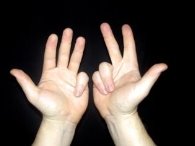
Множимо 6х6. Загинаємо по пальцю на обох руках. Не зігнуті пальці множимо один на одного. 4х4=16. Зігнуті приймаємо за десятки, і складаємо. Це 20.

20+16=36. Разом 6х6=36

Множимо 6х7. Не зігнуті пальці множимо один на одного. 4х3=12. Зігнуті приймаємо за десятки, і складаємо. Це 30. 30+12=42. Разом 6х7=42

Множимо 7х7.

Не зігнуті пальці множимо один на одного. 3х3=9. Зігнуті приймаємо за десятки, і складаємо. Це 40. 40+9=49. Разом 7х7=49

Множимо 7х8.

Не зігнуті пальці множимо один на одного. 3х2=6. Зігнуті приймаємо за десятки, і складаємо. Це 50. 50+6=56. Разом 7х8=56

Множимо 8х8.

Не зігнуті пальці множимо один на одного. 2х2=4.

Зігнуті приймаємо за десятки, і складаємо. Це 60. 60+4=42. Разом

8х8=64

Множимо 8х9.

Не зігнуті пальці множимо один на одного. 2х1=2. Зігнуті приймаємо за десятки, і складаємо. Це 70. 70+2=72. Разом 8х9=72

Множимо 9х9.

Не зігнуті пальці множимо один на одного. 1х1=1. Зігнуті приймаємо за десятки, і складаємо. Це 80. 80+1=81. Разом 9х9=81

Не секрет, що в різних країнах методи викладання різні. Декілька десятиліть тому найсильнішою у світі системою шкільної освіти вважалася радянська. Але навіть в СРСР не використали деякі цікаві методи навчання дітей математиці.

Наприклад, в Японії учні першого класу можуть перемножувати тризначні числа, не знаючи таблицю множення. Для цього використовується простий метод з малюванням смужок. Логіка методу зрозуміла з малюнка.

Багатьом здасться, що такий спосіб японського або китайського множення занадто складений і заплутаний, але це тільки на перший погляд. Саме візуалізація, тобто зображення усіх точок перетину прямих(множників) на одній площині, дає нам зорову підтримку, тоді як традиційний спосіб множення має на увазі велику кількість арифметичних дій

тільки в думці. Китайське або японське множення допомагає не лише швидко і ефективно множити двозначні і тризначні числа один на одного без калькулятора, але і розвиває ерудицію. Погодьтеся, не кожен зможе похвалитися тим, що на практиці володіє прадавнім китайським методом множення(*), який актуальний і прекрасно працює і у сучасному світі.

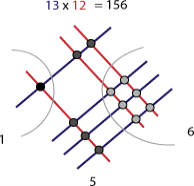
Приклад: помножимо 21 на 13. У першому множнику 2 десятки і 1единица, означає будуємо 2 паралельних прямої і віддалік 1 пряму.

У другому множнику 1 десяток і 3 одиниці. Будуємо паралельно 1 і

віддалік 3 прямої, що перетинає прямі першого множника.

Прямі перетнулися в точках, кількість яких і є відповідь, тобто 13 х 12 = 156

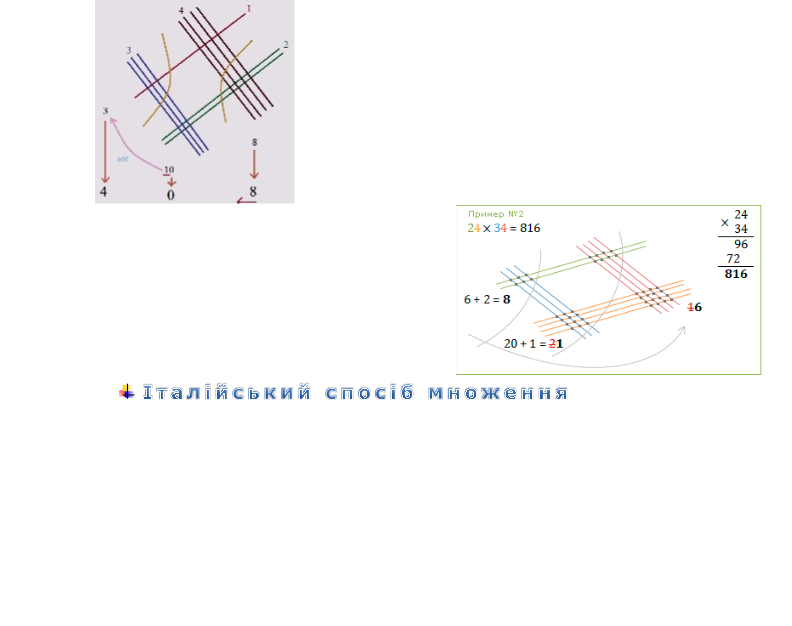
1 2  34 = 408

Приклад : 24 × 34 = 816

В даному прикладі є нюанси ;-) При підрахунку крапочок в першій частині

получилось16. Одиничку отправляем- прибавляем до крапочок другої частини (20 + 1).

Деякі дослідні вчителі в минулому столітті вважали, що цей спосіб повинен замінити в нашій школі загальноприйнятий спосіб множення. Американцям він настільки сподобався, що вони його навіть так і назвали

«Американський спосіб». Проте їм користувалися жителі Індії ще в VI ст н. е., і правильніше за нього на-звати «індійським способом». Перемножити два каких- або двозначних числа, скажемо 23 на 12. Я відразу пишу, що вийде.

х23

12

276

Ви бачите: дуже швидко отримана відповідь. Але як він отриманий?

Перший крок:

х23 говорю: «2 х 3 = 6»

12

..6

Другий крок: х23 говорю: « 2 х 2 + 1×3

12

..76

Я познайомила з цим способом на дуже простому прикладі без переходу через розряд. Проте мої дослідження показали, що їм можна користуватися і при множенні чисел з переходом через розряд, а також при множенні багатозначних чисел. Наведемо приклади:

На Русі цей спосіб був відомий як спосіб множення хрестиком. У цьому

«хрестику» і полягає незручність множення, легко заплутатися, до того ж важко утримувати у голові всі проміжні твори, результати яких потім треба скласти.              Отже, розглянуті нами старовинні способи множення показують, що використовуємий в школі алгоритм множення натуральних чисел не єдиний і відомий він був не завжди. Проте, він досить швидкий і найбільш зручний.

Староєгипетське множення є послідовним методом множення двох чисел. Щоб множити числа, їм не треба було знати таблиці множення, а досить було тільки уміти розкладати числа на кратні підстави, множити ці кратні числа і складати. Єгипетський метод припускає розкладання найменшого з двох множників на кратні числа і подальше їх послідовне перемножування на другий множник(див. приклад). Цей метод можна і сьогодні зустріти в дуже віддалених регіонах.

Розкладання. Єгиптяни використали систему розкладання найменшого множника на кратні числа, сума яких складала б початкове число.

Щоб правильно підібрати кратне число, треба було знати наступну таблицю значень :

1 x 2 = 2

2 x 2 = 4

4 x 2 = 8

8 x 2 = 16

16 x 2 = 32

Приклад розкладання числа 25: Кратний множник для числа "25" - це 16;

25 - 16 = 9. Кратний множник для числа "9" - це 8; 9 - 8 = 1. Кратний

множник для числа "1" - це 1; 1 - 1 = 0. Таким чином "25" - це сума трьох

доданків : 16, 8 і 1.

Приклад: помножимо "13" на "238" . Відомо, що 13 = 8 + 4 + 1. Кожен з цих доданків треба помножити на 238. Отримуємо:

✔ 1 х 238 = 238

✔ 4 х 238 = 952

✔ 8 х 238 = 1904

13 × 238 = (8 + 4 + 1) × 238 = 8 x 238 + 4 × 238 + 1 × 238 = 1904 +

952 + 238 = 3094.

Приклад: 34 ∙ 5=34∙ (1 + 4) = 34∙ (1 + 2 ∙ 2) = 34 ∙ 1+ 34 ∙ 4.

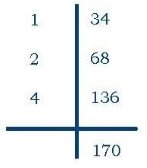Т.к. 5 = 4 + 1, то для отримання відповіді залишалося скласти числа, що стоять в правому стовпчику проти цифр 4 і 1, тобто 136 + 34 =

170.

Практична робота: виготовлення посібника для усної лічби

Школярі зможуть навчитися усно складати і умножати мільйони, більйони і навіть секстильйони з квадрілліонамі. А допоможе їм в цьому кандидат філософських наук Василь Оконешников, за сумісництвом винахідник нової системи усного рахунку. Учений стверджує, що людина здатна запам'ятовувати величезний запас інформації, головне – як цю інформацію розташувати.

На думку самого вченого, найбільш виграшною в цьому відношенні є девятерічная система – всі дані просто розташовують в дев’яти ячейках, розташованих, як кнопочки на калькуляторе.

По думці ученого, перш ніж стати обчислювальним «комп'ютером», необхідно визубрити створену ним таблицю. Цифри в ній розподілені в дев'яти клітках непросто. Як стверджує Оконешников, око людини і його пам'ять так хитро влаштовані, що інформація, розташована по його методиці, запам'ятовується по-перше, швидше, а по-друге – намертво .

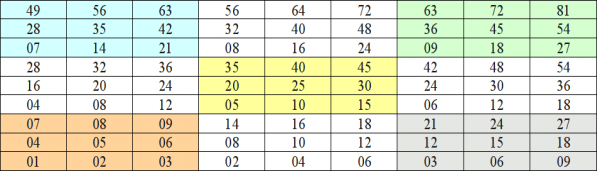
Таблиця розділена на 9 частин. Розташовані вони за принципом міні калькулятора: зліва в нижньому кутку «1», справа у верхньому кутку «9». Кожна частина – таблиця множення чисел від 1 до 9 (знову ж таки в лівому нижньому кутку на 1, поруч правіше на 2 і так далі, по тій же

«кнопковій» система). Як ними користуватися?

Наприклад, потрібно помножити 9 на 842. Відразу згадуємо велику

«кнопку» 9 (вона вгорі справа і на ній в думках знаходимо маленькі кнопочки 8,4,2 (вони також розташовані як на калькуляторі). Ним відповідають числа 72, 36, 18. Отримані числа складаємо особливо: перша цифра 7 (залишається без зміни), 2 в думках складаємо з 3, отримуємо 5 – це друга цифра результату, 6 складаємо з 1, отримуємо третю цифру -7, і залишається остання цифра шуканого числа – 8. В результаті вийшло 7578. Якщо при складанні двох цифр виходить число, що перевершує дев'ять, то його перша цифра додається до попередньої цифри результату, а друга пишеться на «своє» місце.

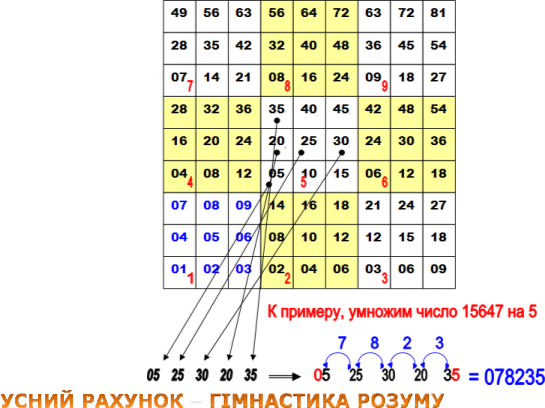За допомогою матричної таблиці Оконешникова за твердженням самого автора, можна вивчати і іноземні мови, і навіть таблицю Менделєєва. Нова методика була випробувана в декількох російських школах і університетах. Міносвіти

РФ дозволило публікувати в зошитах в клітинку разом із звичною таблицею Піфагора нову таблицю множення – доки просто для знайомств Приклад: 15647 х 5

5.1.   Множення і ділення на 4.

Щоб помножити число на 4, його двічі подвоюють.

Наприклад,

214 * 4 = (214 * 2) * 2 = 428 * 2 = 856

537 * 4 = (537 * 2) * 2 = 1074 * 2 = 2148

Щоб число розділити на 4, його двічі ділять на 2. Наприклад:

124 : 4 = (124 : 2) : 2 = 62 : 2 = 31

2648 : 4 = (2648 : 2) : 2 = 1324 : 2 = 662

5.2.   Множення і ділення на 5.

Щоб помножити число на 5, треба його помножити на 10/2, тобто помножити на 10 і розділити на 2.

Наприклад,

138 * 5 = (138 * 10) : 2 = 1380 : 2 = 690

548 * 5 (548 * 10) : 2 = 5480 : 2 = 2740

Щоб число розділити на 5, треба помножити його на 0,2, тобто в подвоєному початковому числі відокремити комі останню цифру.

Наприклад,

345 : 5 = 345 * 0,2 = 69,0

51 : 5 = 51 * 0,2 = 10,2

5.3.   Множення на 25.

Щоб помножити число на 25, треба його помножити на 100/4, тобто помножити на 100 і розділити на 4.

Наприклад, 348 * 25 = (348 * 100) : 4 = (34800 : 2) : 2 = 17400 : 2 =

8700

5.4.   Множення на 1,5.

Щоб помножити число на 1,5, треба до початкового числа додати його половину.

Наприклад,

26 * 1,5 = 26 + 13 = 39

228 * 1,5 = 228 + 114 = 342

127 * 1,5 = 127 + 63,5 = 190,5

5.5.  Множення на 9.

Щоб помножити число на 9, до нього приписують 0 і віднімають початкове число. Наприклад,

241 * 9 = 2410 – 241 = 2169

847 * 9 = 8470 – 847 = 7623

5.6.   Множення на 11.

1. спосіб. Щоб число помножити на 11, до нього приписують 0 і додають початкове число. Наприклад:

47 * 11 = 470 + 47 = 517

243 * 11 = 2430 + 243 = 2673

2. спосіб. Якщо хочеш помножити число на 11, то поступай так: запиши число, яке треба помножити на 11, а  між цифрами початкового числа встав суму цих цифр. Якщо сума виходить двозначне число, то 1 додаємо до першої цифри початкового числа. Наприклад:

53 х 11

Крок 1 - Складаємо дві цифри двозначного числа : 5 + 3 = 8

Крок 2 - Поміщаємо результат між двома числами двозначного числа : 583

59 х 11 = 649

Крок 1 — 5 + 9 = 14

Крок 2 - Перекидаємо одиницю наліво, якщо сума на попередньому кроці виявилася більше 9: 5 + 1 = 6(справа залишається другий символ, в даному випадку це четвірка)

Крок 3 - На перший символ ми одиницю вже перекинули, отримали 6. Далі у нас залишилася 4, яку ставимо в центр, і дописуємо 9: 649

Такий спосіб підходить тільки для множення двозначних чисел.

5.7.   Множення тризначного числа на 101.

Наприклад, 125 * 101 = 12625

(збільшуємо перший множник на число його сотень і приписуємо до нього справа дві останні цифри першого множника)

125 + 1 = 126 12625

Ше приклад: 527 * 101 = (527+5)27 = 53227

5.8.   Зведення в квадрат числа, що закінчується цифрою 5.

Цей прийом допоможе швидко звести в квадрат двозначне число, яке закінчується на 5.

85 х 85 = 7225

Крок 1 - Множимо першу цифру на першу цифру, збільшену на одиницю :

8 x(8 + 1) = 72

Крок 2 - Дописуємо до результату, що вийшов, 25: 7225

45 x 45 = 2025

Крок 1 - 4 х(4 + 1) = 20

Крок 2 - 2025

5.9.     Множення на 5

Більшість людей дуже просто запам'ятовують таблицю множення на 5, але, коли доводиться мати справу з великими числами, зробити це стає складніше. Чи ні? Цей прийом неймовірно простий.

Візьміть будь-яке число, розділіть на 2(іншими словами, поділите навпіл). Якщо в результаті вийшло ціле число, припишіть 0 у кінці. Якщо ні, не звертайте увагу на кому і у кінці додайте 5.

Це спрацьовує завжди:

2682×5 = (2682 / 2) & 5 або 0

2682 / 2 = 1341(ціле число, тому додайте 0)

13410

Давайте спробуємо інший приклад:

5887×5

2943,5(дробове число, пропустіть кому, додайте 5)

29435

5.10.   Підрахунок чайових

Якщо вам треба залишити 15% чайових, є простий спосіб зробити це. Вирахуйте 10%(розділіть число на 10), а потім додайте число, що вийшло, до його половини і отримайте відповідь:

15% від $25 = (10% від 25) + ((10% від 25) / 2)

$2.50 + $1.25 = $3.75

5.11.  Складне множення

Якщо вам треба множити великі числа, причому одно з них - парне, ви можете просто перегрупувати їх, щоб отримати відповідь:

32×125 все одно, що : 16×250 все одно, що :

8×500 все одно, що :

4×1000 = 4,000

5.12.  Віднімання з 1000

Щоб виконати віднімання з 1000, можете користуватися цим простим правилом: Відніміть від 9 усіх цифр, окрім останньої. А останню цифру відніміть від 10:

1000-648

Крок 1: від 9 відніміть 6 = 3

Крок 2: від 9 відніміть 4 = 5

Крок 3: від 10 відніміть 8 = 2

Відповідь: 352

5.13.   Множення чисел, трохи менших 100

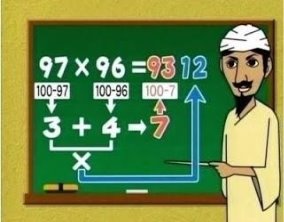Перемножимо 2 числа, трохи менші сотні :

(100 - a)(100 - b) = 10000 - 100(a +

b) + ab = 100(100 -(a + b)) + ab

Наприклад:

81*97 =

a = 19, b = 3, a + b = 22, ab = 57,

100 -(a + b) = 78.

88*89 =

Відповідь: 7857

Слід бути уважним у разі, коли ab виявиться тризначним:

a = 12, b = 11, a + b = 23, ab = 132, 100 -(a + b) = 77.

В цьому випадку треба буде першу цифру від 132 додати до 77, а вже двуцифрове закінчення приписати до отриманого результату. Отримаємо: 7832.

5.14.  Ділення тризначних чисел, що складаються з однакових цифр, на число 37.

Результат дорівнює сумі цих однакових цифр тризначного числа. Наприклад:

а) 222 : 37 = 6, т. к. 2 + 2 + 2 = 6.

б) 333 : 37 = 9, т. к. 3 + 3 + 3 = 9.

в) 777 : 37 = 21, т. к 7 + 7 + 7 = 21.

г) 888 : 37 = 24, т. к. 8 + 8 + 8 = 24.

1 х 1 = 1

11 х 11 = 121

111 х 111 = 12321

1111 х 1111 = 1234321

11111 х 11111 = 123454321

111111 х 111111 = 12345654321

1111111 х 1111111 = 1234567654321

11111111 х 11111111 = 123456787654321

111111111 х 111111111 = 12345678987654321

1 х 9 + 2 = 11

12 х 9 + 3 = 111

123 х 9 + 4 = 1111

1234 х 9 + 5 = 11111

12345 х 9 + 6 = 111111

123456 х 9 + 7 = 1111111

1234567 х 9 + 8 = 11111111

12345678 х 9 + 9 = 111111111

123456789 х 9 + 10 = 1111111111

9 х 9 + 7 = 88

98 х 9 + 6 = 888

987 х 9 + 5 = 8888

9876 х 9 + 4 = 88888

98765 х 9 + 3 = 888888

987654 х 9 + 2 = 8888888

9876543 х 9 + 1 = 88888888

98765432 х 9 + 0 = 888888888

1 х 8 + 1 = 9

12 х 8 + 2 = 98

123 х 8 + 3 = 987

1234 х 8 + 4 = 9876

12345 х 8 + 5 = 98765

123456 х 8 + 6 = 987654

1234567 х 8 + 7 = 9876543

12345678 х 8 + 8 = 98765432

123456789 х 8 + 9 = 987654321

Фокус з цифрами. Нерозлучні двійки

1.   Пусть ваш друг напишет в ряд три разные цифры от 1 до 9.

Например: 6, 3 и 1.

2.   Ниже нужно записать двузначные числа, которые получаются из этих цифр. Таких чисел может быть только шесть. 13, 31, 16, 61,

36, 63

3. Теперь предложите ему сложить задуманные числа: 6+3+1=10 4. Затем нужно              сложить              все              двузначные              числа:

13+31+16+61+36+63=220

5.      И,  наконец, попросите друга разделить вторую сумму на первую              220:10=22

6.   К удивлению товарища, вы называете ему правильный ответ – 22. Причём, какие цифры не возьми, ответ всегда один и тот же  –  22!

Вот вам и неразлучные двойки

Пятерка! Задача фокусника (т.е. твоя) - угадать число, которое получится после нехитрых математических вычислений у твоего друга.

Попроси друга:

• загадать любое число (например, 4)

• прибавить к нему следующее по порядку число (4+5 =9)

• к сумме прибавить 9 ( 9+9 = 18)

• разделить результат пополам (18:2 = 9)

• из результата вычесть задуманное число (9-4 = 5)

А потом ты, как заправский фокусник, угадаешь, сколько получилось! А получится 5! Что самое удивительное, результат всегда будет одинаковым. Можете сами попробовать, чтобы поверить в это.

Відгадати дату народження.

Фокус навчить, як відгадати дату народження. Секрет фокусу:

Отже, для початку треба обрати "жертву", після чого попросити її про себе порахувати:

1. День свого народження (про себе) помножити на два.
2. До результату додати 5.
3. Отриманий результат помножити на 50.
4. Додати номер місяця, в якому народився.

Попросіть людини сказати число. Потім просто відняти 250

від отриманого, і готово. Вийде 4 або 3 цифри. Перші 2 (може бути і одна цифра) - день, а дві останні – місяць народження.

Вірна сума.

Для фокуса потрібні лише

два гральних кубики. Киньте їх на стіл. Нижні межі кубиків Вам

не видно. Візьміть кубики і покажіть ці грані глядачеві. Нехай він складе невидимі Вам очки. Відкладіть кубики в сторону і правильно назвіть шукану суму двох нижніх граней.

Секрет фокусу:

Для цього вам потрібно знати, що на гральних кубиках сума протилежних с торін дорівнює семи. Якщо з одного боку 2 очка, значить, з іншого -

буде 5. Вам видно верхню сторону кубиків. Припустимо, з вашого боку 4 і

1, тобто в сумі - 5. А загальна сума

двох протилежних сторін на обох кубиках дорівнює 14. Значить, щоб назвати суму, відому глядачеві, від 14 відніміть 5. Назвіть її -

9. Адже на гранях кубиків, які бачив глядач, було 3 і 6 очок.

Сума непарних чисел.

Просіть глядача за 1 хвилину порахувати суму

всіх непарних чисел від 0 до 20 (безкалькулятора). Швидше за все він не встигне. Говорите:

- Ну ти і черепаха, спробуй ще раз, тільки хутчій, яка сума непарних від 0 до 45 включно?

Швидше за все глядач відмахнеться, мовляв я до 20 то не зміг, а тут до 45 (тутуже можна і з калькулятором, але знову таки зробити обмеження в часі, щоб він ну ніяк не встиг). Ви ж легко рахуєте суму всіх непарних, навіть багатозначних чисел (тільки хто перевіряти буде).

Секрет фокусу:

Потрібно до останнього (заданого) непарного числа додати 1, поділити на 2 і піднести до квадрату.

Приклад: від 1 до 49 включно 49 +1 = 50, 50/2 = 25, 25 * 25 = 625.

Якщо Вас попросять порахувати вже дуже велике число, то Вам доведеться таки

скористатися калькулятором, але оскільки рахувати дуже мало, Ви це зробите за 10-15сек.

Знову і знову П'ЯТЬ.

Простенький і коротенький фокус, де фокуснику навіть не треба нічого рахувати і думати.

Просіть задумати будь-яке число (хоч 50-ти значне),

потім просите додати до нього наступне по порядку, потім хай додасть до суми 9, розділить отримане навпіл, і відніме

від результату задумане ним число. Ви легко називаєте число, яке у нього вийшло!

Секрет фокусу:

Ви легко вгадуєте скільки у нього вийшло, тому що, яке б він число не загадав, після всіх підрахунків у нього завжди буде 5.

Приклад: загадали 26, 26 +27 = 53, 53 +9 = 62, 62/2 = 31, 31-26 = 5.

Загадали 565, 565+566 = 1131, 1131 + 9 = 1140, 1140/2 = 570, 570-

565 = 5.

Загадали 44444,

44444+44445 = 88889, 88889 +9 = 88898, 88898/2 = 44449, 44449-

44444 = 5.

Додавання чисел Фібоначчі

Числами Фібоначчі називають ряд чисел, в якому кожне,починаючи з третього, є сумою двох попередніх.

Секрет фокусу:

Цей фокус демонструють так: показує просить когось записати одне під одним двоє будь-яких чисел, які він забажає.

Припустимо для прикладу, що були обрані 8 і 5. Потім глядач

повинен скласти ці числа. Знайдене таким чином третє число складається з другим (тим, що стояло попереду), і виходить четверте

число. Цей процес повторюють до тих пір, поки в вертикальному стовпці не виявиться десять чисел: 8, 5, 13, 18, 31, 49, 80, 129, 209, 338.

Під час запису чисел той, хто показує фокус, стоїть, повернувшись до глядачів спиною. Коли всі числа будуть записані, він повертається, проводить під колонкою цифр риску і, не замислюючись, підписує суму цих чисел. Щоб отримати цю суму, йому потрібно

просто взяти четверте число знизу і помножити його на 11 - операція, яку неважко виконати в пам'яті. У нашому випадку четвертим числом буде 80, тому у відповіді вийде число 80, взяте 11 разів, тобто 880.

Живий комп'ютер

Ви просите когось із глядачів написати в стовпчик двоє десятизначних чисел (чим більше значення числа, тим

ефектніший фокус), потім під ними пишете своє число, підводите риску і миттєво записуєте відповідь.

Другий варіант цього фокусу: після того як Ви написали своє число просите глядача, щоб під Вашим числом він написав ще

десятизначне число, а потім знову пишіть своє і миттєво видаєте результат.

Секрет фокусу:

Коли Ви пишете своє число, то обираєте його не довільно - сума кожної цифри цього числа повинна скласти з кожною цифрою числа глядача 9. Таким чином у Вас виходять не три різних

десятизначних числа, а два з яких одне матиме всі дев'ятки. А значить Ви миттєво можете написати результат: треба просто переписати перше число глядача і поставити перед ним

одиницю, а від останньої цифри відняти одиницю!

Приклад: 4563843274 + 7498854231 + 2501145768 = 14563843273

Навіть якщо математику не була вашим улюбленим предметом, складно посперечатися з тим фактом, що вона відіграє величезну роль у нашому житті. Хоча числа оточують нас всюди, деяким з них ми надаємо особливого значення.

Ось декілька цікавих фактів про число Пі, золотий перетин, щасливих і нещасливих, а також найбільших числах.

1.   Число Пі

Число Пі - це найвідоміша і загадкова математична константа, яка виражає співвідношення кола до діаметру кола.Його використовують у світовій статистиці, прогнозі погоди і інших ситуаціях, що вимагають великої обчислювальної потужності.

Воно ніколи не повторюється і ніколи не закінчується, якщо його записати у вигляді десяткового дробу.

Цікаво, що відома піраміда Хеопса є втіленням числа Пі, так як співвідношення її висота з периметром підстави дає число Пі.

Перші 100 знаків після коми числа Пі виглядають так:

3,1415926535897932384626433832795028841971693993751

058209749445923078164062862089986280348253421170679

2.   Число 666

Число 666 найбільше відоме тим, що вважається числом звіра або числом диявола в Біблії, де згадується: "Тут мудрість. Хто має розум, нехай порахує число звірине, бо число це людське; число його шістсот шістдесят шість".

Багато хто вважає це число приносить нещастя, сатанинським знаком антихриста і уникають його. Боязнь числа 666 називається гексакосиойгексеконтагексафобія. Є й ті, хто вважає, що насправді переклад був неточним і числом звіра є 616.

3.   Число гугол і гуолплекс

Число Гугол, яке представляє собою одиницю з 100 нулями, стало відомим завдяки відомій пошуковій системі Google, яка злегка спотворила назву числа "гугол" (Googol).

Від нього число "гуголплекс", яке представляє собою 10 в ступені гугол. Наскільки велике це число? Якщо весь Всесвіт наповнити аркушами паперу і на кожному написати "нулі", то виявиться, що ми написали лише половину цього числа.

4.   Нуль

Нуль став основою сучасної математики. Хоча ми починаємо рахувати з одиниці, математики і програмісти рахують з нуля.

Він відомий, як нейтральний елемент. Якщо ви додасте до або відніміть від будь-якого числа нуль, число не зміниться. Якщо помножити будь-яке  число  на  нуль,  ви  отримаєте нуль.

Будь-яке число, зведене в ступінь 0

дорівнюватиме 1, наприклад, 2 в нульової ступеня дорівнює 1. Але ви не можете розділити число на нуль.

Не існує нульового року в системі числення. Так, йде 3 рік до н.е., 2 рік до н.е., 1 рік до н.е., а потім 1 рік н.е., 2 рік н.е. і так далі.

5.   Число 7

Число 7 вважається самим щасливим числом. Існує 7 днів у тижні, 7 смертних гріхів і сім чеснот, 7 континентів, 7 кольорів веселки, 7 музичних нот, 7 днів Творіння і багато іншого.

У Європі є повір'я, згідно з яким 7-ий син 7- го сина              володіє              магічною              силою.              Також

число 7 найчастіше є улюбленим числом людей у всьому світі.

7.   Число 5

Згідно Піфагору, число 5 - це досконале число людського мікрокосму. Аристотель також додав 5-й елемент до 4-х стихій (вогонь, вода, повітря, земля) і назвав його ефіром, що стало основою більшості духовних практик стародавніх алхіміків. Також число 5 має духовне значення і символізм в інших культурах.

Цікаво, що воно стало основою псевдорелігії

•       діскордіанізма, згідно з якою все, що відбувається у Всесвіті, пов'язано з числом п'ять.

8.   Число 8

Число 8 вважається числом досконалості. Воно асоціюється з нескінченністю, а у древніх єгиптян вважалося числом рівноваги і космічного порядку.

Воно вважається щасливим числом у японській і китайській культурі.

Піфагорійці вірили, що число 8 є символом любові і дружби.

9.    Число 13

зрадив Ісуса.

Число 13 стало символом поганого передвістя поряд з популярністю п'ятниці 13-те. Навіть у наші часи, ви можете помітити, що в багатьох будівлях відсутній 13-й поверх.

Число 13 має релігійне походження у християн, так  як  під  час   таємної  вечері 13-й апостол

10.   Числа Фібоначчі

Ці числа були названі на честь італійського математика Леонардо Пізанського, відомого як Фібоначчі, який познайомив Європу з десятковою системою числення і арабськими цифрами.

Числа Фібоначчі представляють собою числа послідовності в наступному прядці:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...

При цьому кожне наступне число дорівнює сумі двох попередніх чисел. Послідовність              Фібоначчі              спостерігається              у              природі              рослин              і              тварин,              у візерунку насіння соняшника, ананасі, сосновій шишці і навіть тілі людини (один ніс, два ока, три сегменти кінцівок, п'ять пальців на руці).

Походження життя – це та загадка, відгадавши я математики задають її характеристикику, людство б пояснило одну з найскладніших саморегулюючих систем. Ось як за допомогою математики задають її характеристики.

Організм людини складається із 1017 клітин, її мозок містить 1030 елементарних частинок. 10млрд. її клітин забезпечують приблизно 210000000000 різних станів, а кількість зв’язків між нейронами лише однієї тисячної частини мозку становить 2287300.

Загальна довжина кровоносних судин становить 100000 км. Кожний еротроцит містить близько 270000000 одиниць гемоглобину тощо.

Цікві вправи

Задача 1. Відношення головного мозку до спінного риб становить 1:1, у коня – 2,5:1, у собаки від 4,5:1 до 9:1, а улюдини – 40:1. Який висновок можна з цього зробити?

Задача 2. Наше серце робить ≈ 70 ударів на хвилину. При кожному ударі воно, як насос, перекачує 100г крові. Скільки крові перекачає серце за добу? За І семестр? (≈ 10 тис. літрів; 1млн.230тис. літрів).

Задача 3. З перукарні я вийшов підстриженим під «нулівку». Іду і радію. А на зустріч приятель. Привітався і питає:

• Що ж ти стільки волосся на голові залишив? Скільки, по-твоєму, метрів волосся в тебе залишилося після такої стріжки?

• Метр-два, може й набереться, - відповів я, - якщо додати усі залишки.

• Помиляєшься, й дуже, - розсміявся приятель. – Подумай, перш ніж відповісти на таке, здавалось би, просте запитання. (≈ 200м, коли вважати, що лишилися волосини завдовжки 1мм, а їх число в середньому становить 200000).

Задача 4. Пульс здорової людини становить 4200 ударів за годину. Скільки ударів серця відбудеться у такої людини протягом І семестру? (≈ 12млн. ударів).

Задача 5. Відношення відносних розмірів головного мозку до маси тіла у людини становить 1:50. Яка маса головного мозку у людини масою 70 кг?

Задача 6. В організмі людини маса залоз різна. Наприклад, щитовидна залоза досягає 35г, гіпофіз – 1г, надниркові залози – 10г кожна. Який відсоток становить загальна маса цих залоз відносно тіла дорослої людини масою 75 кг?

Задача 7. Маса щитовидної залози становить 30г. За одну хвилину через судини залози проходе крові у 5 разів більше, ніж маса самої залози.

Скільки крові проходе через залозу за 1сек. і за 1 год?

Задача 8. Яка вага вашого скелету, якщо він становить 18% загальної маси вашого тіла?

Задача 9. Повний кругообіг крові у дорослої людини здійснюється за 25 сек., у дитини – за 15 сек., у підлітка – за 18 сек. Скільки раз пройде кров по тілу людини за добу?

Задача 10. 1г гемоглобіна реально зв’язує 1,34мл кисню. В одному літрі крові міститься в середньому 150г гемоглобіну. Скільки кисню міститься в одному літрі крові?

Неймовірно, але якщо помножити Твій вік на 7, а потім — на 1443, то результат Тебе неодмінно здивує — Ти отримаєш свій вік, написаний три рази підряд. Перевіримо?

Цікаво, що у будь-якій групі з 23-х і більше людей більш за все знайдуться двоє, які відзначають свій День народження в один і той же день. Вірогідність такого збігу перевищує 50%.

Друже, а Ти знаєш, що мить — це насправді одиниця виміру часу, яка триває

близько однієї сотої долі секунди?

Древні римляни, безперечно, були дуже розумним, математично освіченим народом, та все ж про дещо вони забули. А саме про

«нуль». Нуль — це єдине число, яке не можна написати римськими цифрами.

Сума чисел від 1 до 100 дорівнює 5050. А хтось із Твоїх друзів знає про це?

А ось іще одна математична цікавинка. З 1995-го року у місті Тайбей на Тайвані

мешканцям дозволили видаляти цифру «чотири» у ліфтах. Вся справа у тому, що вона звучить аналогічно до слова «смерть». Тож у багатьох будинках немає… четвертого поверху!)

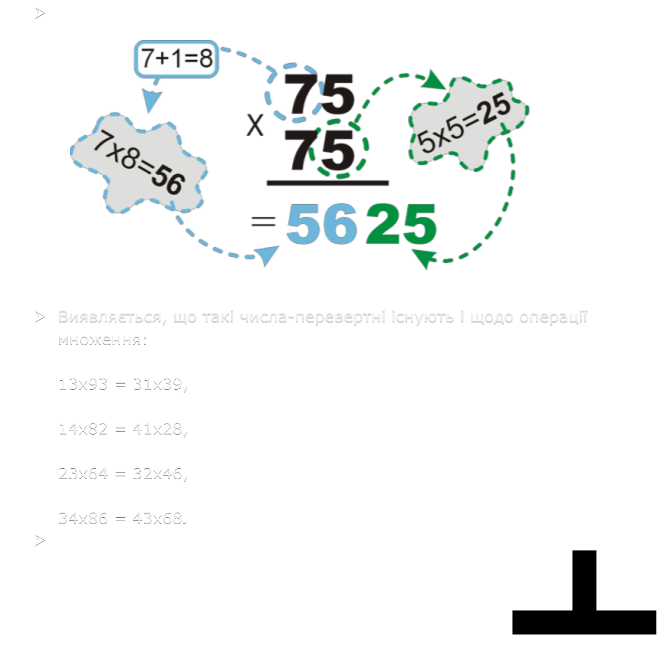• Множення двоцифрових чисел, що закінчуються цифрою

• Виявляється, що такі числа-перевертні існують і щодо операції множення:

13х93 = 31х39,

14х82 = 41х28,

23х64 = 32х46,

34х86 = 43х68.

• Ортодоксальні євреї вилучають з повсякденного обігу будь-які християнські символи. Навіть займаючись математикою, вони відмовляються від накреслення прийнятого у всьому світі знака

«плюс», недописуючи його. В результаті виходить перевернута буква «т».

Один з найпоширеніших наукових міфів пов’язаний з тим, чому все- таки Альфред Нобель позбавив

математиків можливості отримувати премію свого імені. Побутує версія, що дружина вченого нібито зрадила йому з математиком. Але річ у тім, що Нобель ніколи не був одружений і взагалі зробив вибір між наукою і жінками на користь першої … Більш правдоподібна версія пов’язана з тим, що на момент появи Нобелівської премії у

математиків вже була «своя» схожа нагорода, що вручається шведським королем. Є також думка, що Нобель не вважав математику повноцінною наукою, оскільки вона складається лише з теоретичних розмірковувань.

Ми знаємо про Лермонтова як про блискучого поета і прозаїка. Але, крім літератури, він захоплювався ще й математикою. І у вільний від творчості час любив вирішувати завдання з вищої математики та аналітичної геометрії.

18 – єдине число, сума цифр якого вдвічі менша від нього самого. Льюїса Керролла ми знаємо передусім як автора двох “Аліс” – в Країні Чудес і в Задзеркаллі, хоча про себе ця людина говорить передусім як про вченого. І був досить

відомим у наукових колах професором математики, чим дуже розчарував англійську королеву. Прочитавши тільки-но видану

«Алісу», королева була в захваті і звеліла принести їй інші роботи талановитого автора. Яким же ж було її здивування, коли ними виявилися праці з математики! До слова, крім виконання обов’язків викладача математики і

логіки при Оксфордському університеті, Керролл працював ще й університетським дияконом.

Німець Ернст Куммер – великий знавець теорії чисел, що оперував складними математичними поняттями, – не міг виконати найпростіші арифметичні дії.

Багато майбутніх відомих математиків погано поводилися в школі і не відрізнялися хорошою успішністю. В аутсайдерах значилися, наприклад, Джеймс Максвелл, Рамануджан Срініваса і Василь Цингер. Плентався позаду ледь-ледь успішних й Ісаак Ньютон.

Причому взявся він за розум тільки після того, як один з його однокласників-відмінників назвав його дурнем.

Хочеш навчитися визначати номер телефону своїх друзів, не зазираючи в записник? Це дуже просто! Потрібно лише зробити кілька простих математичних дій! Сьогодні я розкажу Тобі таємницю цих загадкових чисел.

Для математичного фокусу Тобі, а точніше Твоєму другові, знадобиться калькулятор — без нього не вийде.

1. Попроси друга ввести в калькулятор перші три цифри його

телефону, не називаючи їх уголос.

Але код мобільного оператора пропускаємо (приміром, 098 чи 095).

2. Тепер нехай він помножить ці цифри на 80.
3. Потім потрібно додати до результату 1.
4. Далі — помножити число, яке вийде, на 250.
5. До результату треба додати 4 останні цифри номеру друга. Знову ж таки, їх він не повинен Тобі говорити.
6. І… ну добре, нехай він додасть ці чотири цифри ще раз.
7. Попроси відняти від результату 250.
8. А тепер нехай друг розділить число на 2.

І що ж вийшло? В цьому наборі чисел Твої друзі та рідні мають впізнати свій телефонний номер. Фокус цей простий та цікавий. Він обов’язково сподобається Твоїм знайомим та змусить їх усміхнутися.

• Вперше, від'ємні числа, як поняття, були введені в 1202 році, італійським купцем Пізано. Він перший почав з їх допомогою позначати борги і збитки в торгівлі.

Наприкінці XIX ст італійський фізіолог Анджело Моссо (1846-1910) зрівноважив людину, яка спокійно лежала на спеціальних, дуже чутливих вагах, так, що обидві половини

тулуба були строго паралельні підлозі. Коли ця людина почала розв'язувати арифметичні зaдaчі, головa його стaлa важче і переважила. Тaк було показано, що розумова праця пов'язана з припливом крові до мозку. І саме на цю гіпотезу спирається головний сучасний

метод вивчення мозкового забезпечення психічної діяльності, -

функціональна магнітно-резонансна томографія.

Символ «+» з’явився з латинського слова «Net» (союз). При скорописі букву «е» пропускали. Буква «t», яка залишилась, з часом і перетворилась в знак «+».

Радянський розвідник майор Віхр (з відомого фільму) існував насправді і після війни працював учителем математики в одному невеличкому українському містечку.

• Чи знаєте ви, що О. С. Пушкін написав такі рядки : «Натхнення потрібне в геометрії, як і в поезії».
• Наполеон Бонапарт писав математичні роботи і один геометричний факт називається «Задача Наполеона».
• Шарль Перро, автор «Червоної Шапочки», написав казку «Любов до циркуля і лінійки».

Одне з самих загадкових творів образотворчого мистецтва зберігається в Кунстхалле міста Карлерує. Мова іде про гравюру Альбрехта Дюрера «Меланхолія 1» (1514р.).

Важлива деталь, зображена на гравюрі

«Меланхолія 1» - складений вперше в європейському мистецтві магічний квадрат 4×4.

Сума чисел в будь-якому ряду або стовбці дорівнює 34. Два середніх в нижньому ряду вказують дату створення картини 1514.

Протягом тисячоліть люди користуються числами для

різноманітних підрахунків і обчислень. Світ чисел містить велику кількість красивих і загадкових речей.

Однією з цікавих проблем є задача про «Магічний квадрат». «Магічним» його називають тому, що він має дуже цікаву особливість. Числа, що входять до його складу, утворюють однакові суми в усіх рядках, стовпчиках і діагоналях.

Ось приклад такого квадрата:

Суми чисел у рядках дорівнюють 24:

11+ 1+ 12=24

9+8+7=24

4+15+5=24

Так само суми чисел у стовпчиках дорівнюють 24.

І суми чисел, що стоять на діагоналях, також мають ту ж саму властивість:

11+8+5=24

12+8+4=24

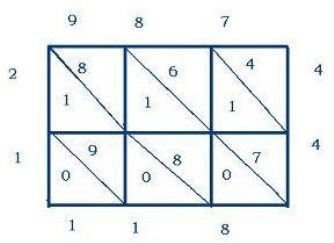
Ось ще приклади «магічних» квадратів. Розгляньте їх. Переконайтесь, що ці квадрати дійсно «магічні».

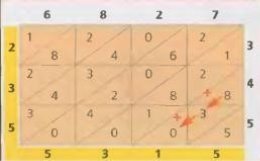
Як створити такий квадрат? Як підібрати числа, щоб вони відповідали властивостям «магічних» квадратів? Давайте спробуємо це зробити.

Нехай є квадрат, до якого вписані чотири числа.

Обчисливши суму в рядку, знайдемо, що вона дорівнює 21:

6+7+8=21. Отже, всі суми мають бути саме такими. Щоб вписати число у правий верхній куточок, ми додаємо числа по діагоналі

4+7=11

Очевидно, щоб сума чисел цієї діагоналі дорівнювала 21, в правому верхньому куточку слід написати число 10. Квадрат стане таким (рис. 2).

Таким самим чином можна знайти число у лівому верхньому куточку:

6+4=10 21-10=11

Тепер квадрат матиме вигляд.

Міркуючи аналогічним чином, визначте, як заповнити решту клітинок, щоб квадрат став «магічним» .

Практична робота

♦ Попрацюйте з програмою Магічний квадрат. Виберіть перший рівень складності і заповніть запропоновані вам «магічні» квадрати.

• Нормальний — магічний квадрат, заповнений цілими числами від 1 до п2.
• Напівмагічний — магічний квадрат, заповненний числами від 1 до п2 , причому сума чисел по горизонталях і вертикалях дорівнює магічній константі, а по діагоналях ця умова не виконується.

• Асоціативний, або симетричний — магічний квадрат, у якого сума будь-яких двох чисел, що розташовані симетрично відносно центра квадрата, дорівнює одному й тому ж числу: .1 + п2

• Пандіагональний,або диявольський — магічний квадрат, в якого сума чисел по ламаних діагоналях також дорівнює магічній константі.

• Ідеальний — магічний квадрат, що одночасно є пандіагональним і асоціативним.

• Досконалий — магічний квадрат четвертого порядку, що є пандіагональним та має ряд додаткових властивостей. Всі магічні квадрати 4 порядку є досконалими.

• Бімагічний — магічний квадрат, що залишається магічним після заміни всіх його елементів на їх квадрати. Бімагічних квадрати 3, 4 і 5 порядків не існує.

• Мультимагічний — узагальнення властивостей бімагічних квадратів на довільний степінь п.

• Квадрати Б. Франкліна— магічні квадрати, які крім основних властивостей мають додаткові унікальні особливості.

«Світ побудований на силі чисел» - був упевнений великий математик минулого Піфагор, що заснував релігійно-філософське вчення, яке проголосило кількісні відношення основою сутності речей. Окремі явища і події розглядалися з точки зору числових варіацій. І на підставі цих зв`язків і комбінацій виникла наука нумерологія, розвитком і вивченням якої займався старогрецький математик і філософ Піфагор. Він

же і створив так званий квадрат Піфагора, що дозволяє визначити число долі. Головний принцип нумерології базується на тому, що всі складні числа можна звести до простих - цифрам від 1 до 9. А цим цифрам, від 1 до 9, нумерологія приписує певні властивості, образи і поняття.

Якщо розглядати нумерологію з точки зору езотерики, то вона допомагає визначити число долі або характеру. Таке число дає загальні уявлення про людину, його таланти, сильні сторони і слабких. Крім того, воно може підказати майбутнє, дати відповіді на питання, що цікавлять людини питання і допомогти з прийняттям рішення. Зокрема, використовується квадрат Піфагора.

Протягом тривалого періоду часу люди вивчали числа. Перші спроби пояснення долі людини за допомогою чисел відносяться до періоду стародавнього Вавилона. Уже тоді за допомогою нескладних таблиць і простих маніпуляцій намагалися з`ясувати сьогодення і майбутнє.

Систематизувати ж знання вдалося ближче до VI століття до нашої ери Піфагору. Вчений зміг зібрати знання різних народів і об`єднати їх в одну с Існує величезна безліч методів скорочення великих чисел до простих, елементарних. Але найпростіший і загальнодоступний - це метод складання. Він ґрунтується на тому, що потрібно скласти всі десяткові розряди числа, а потім, якщо утвориться число більше десяти, повторити процедуру. Загалом, повинно вийти число від 1 до 9. Хоча деякі в нумерологічних розрахунках залишають і окремі двозначні цифри, типу 11, 22 і так далі. истему, знайому нам під терміном «нумерологія».

Система Піфагора

Квадрат Піфагора - система, за допомогою якої можна дізнатися число долі. Грунтується дана система на дату народження.

Розрахуємо квадрат Піфагора за датою народження 11 липня 1953 року. Ряд цифр буде наступним: 11.07.1953. Тепер займаємося обчисленням основних цифр: 1+1+7 = 9. Складемо цифру року: 1+9+5+3=18. Складемо отримані числа: 9+18 = 27. Отже, 27 – наше перше робоче число. Складемо цифри першого робочого числа: 2+7 = 9. А 9 друге робоче число. Тепер від першого робочого числа слід відняти першу цифру дня народження: 27-2 = 25. 25 третє робоче число. Потім складемо цифри третього робочого числа: 2+5 = 7 – це четверте робоче число.

Наш перший ряд цифр – дата народження 11.7.1953 Другій ряд складається з робочих чисел: 27.9.25.7

Тепер слід підрахувати кількість цифр у двох рядах: 13.ця цифра вже дає нам перші дані. Ось що вона означає: Я ПРИЙШОВ НА ЗЕМЛЮ 13-Й РАЗ. А всього, як вважав Піфагор, людина має приходити на землю тільки 15 разів. А потім людина переходить в інший, більш досконалий вимір.

Отже, маємо таблицю, в кожен квадрат якої вписуємо однакові цифри з двох рядів чисел. Ось що вийшло:

Таблиця, яку ми склали для прогнозу за принципом Піфагора, називається

– психоматиця. Для того, щоб зрозуміти отриману психоматрицю, необхідно звернутися до роз шифровки.

111 – відрізняється хорошим характером і вмінням знайти спільну мову практично з будь-якою людиною.

22 – сильна біоенергетика, якою можна поділитися.

3 – людина настрію, у якого все може змінюватися в залежності від відчуттів.

Немає 4 – слабке здоров’я.

55 – дуже розвинена інтуіция.

Немає 6 – індивідум, для якого важлива праця.

777 – яскраве, але часто коротке життя. Немає 8 – повна відсутність почуття обов’язку. 99 – тямущий чоловік з самого народження.

Ознака подільності – це правило, що дозволяє швидко визначити, чи є число кратним заздалегідь заданому числу, без необхідності виконувати ділення.

Розглянемо кілька основних ознак поділу: ознака подільності на 2 – число ділиться на 2 тоді і тільки тоді, коли його остання цифра ділиться на 2, тобто є парною;

ознака подільності на 3 – число ділиться на 3 тоді і тільки тоді, коли сума його цифр ділиться на 3;

ознака подільності на 4 – число ділиться на 4 тоді і тільки тоді, коли число з двох останніх цифр нулі або діляться на 4;

ознака подільності на 5– число ділиться на 5 тоді і тільки тоді, коли остання цифра 5 або 0;

ознака подільності на 6– число ділиться на 6 тоді і тільки тоді, коли воно ділиться на 2 і на 3;

ознака подільності на 7– число ділиться на 7 тоді і тільки тоді, якщо виконується одне з правил:

1. Якщо потроєна сума десятків разом з одиницями ділиться на 7 (наприклад, перевіримо число 112 ділиться на 7; 3·11 + 2 = 35, 35 ділиться на 7);
2. Якщо сума подвоєного числа без останніх двох цифр і останніх двох цифр ділиться на 7 (наприклад, 168 ділиться на 7, так як 2·1 + 68 = 70, 70 націло ділиться на 7);
3. Якщо сума числа без останньої цифри і останньої цифри, помноженої на 5, ділиться на 7 (161 ділиться на 7, оскільки 16 + 1·5 = 21, 21 націло ділиться на 7)

Правило подільності на 7 для великих чисел – число розбивають уявно на блоки по три цифри, починаючи з останньої цифри. Згідно правила, якщо різниця суми блоків, що стоять на парних місцях, і сума блоків, що стоять на непарних місцях, ділиться на 7, то і число ділиться на 7 (наприклад, 14561274; 561 – (14 + 274) = 273; перевіримо 237 за правилом 2*: 2·2 + 73 = 77, це число «красиво» ділиться на 7 )

ознака подільності на 8 – число ділиться на 8 тоді і тільки тоді, коли три його останні цифри нулі або утворюють число, яке ділиться на 8; за цим правилом ви не перевірите чисел до 1000, однак до них можна тричі застосовувати ознаки подільності на 2; (наприклад, для числа 864 розклад на прості множники буде наступним: 864:2=432; 432:2= 216; 216:2 = 108. Отже, 864 ділиться на 2·2·2=8)

ознака подільності на 9– число ділиться на 9 тоді і тільки тоді, коли сума його цифр ділиться на 9;

ознака подільності на 10– число ділиться на 10 тоді і тільки тоді, коли воно закінчується нулем;

ознака подільності на 11– число ділиться на 11 тоді і тільки тоді, якщо на 11 ділиться сума чисел, що утворені парами цифр запису числа, починаючи з одиниць. (Наприклад: 103785, складаємо суму: 10+37+85=132, 01+32=33, 33 ділиться на 11, отже й число 103785

ділиться на 11);

ознака подільності на 12– число ділиться на 12 тоді і тільки тоді, коли воно ділиться на 3 і на 4;

ознака подільності на 13– число ділиться на 13 тоді і тільки тоді, коли сума числа десятків з кількістю одиниць, помноженою на 4, ділиться на 13 (наприклад, число 845 містить 84 десятки й 5 одиниць, складаємо суму 84+5·4=104, далі: 10+4·4=26 – ділиться на 13, отже й число 845 ділиться на 13);

ознака подільності на 14– число ділиться на 14 тоді і тільки тоді, коли воно ділиться на 2 і на 7;

ознака подільності на 15– число ділиться на 15 тоді і тільки тоді, коли воно ділиться на 3 і на 5;

ознака подільності на 17– число ділиться на 17 тоді і тільки тоді, коли число без останніх двох цифр множать на 2 і додають число, утворене останніми двома цифрами. (Наприклад, 187:1·2+87=85, 85 ділиться на 17). Від числа без останньої цифри віднімають останню цифру, помножену на 5. (Наприклад, 85:8-5·5=-17, результат повинен ділитись на 17);

ознака подільності на 19– число ділиться на 19 тоді і тільки тоді, коли до числа без останньої цифри додають подвоєну останню цифру. (Наприклад, 437:43+7·2=57, результат повинен ділитись на 19);

ознака подільності на 23 – число ділиться на 23 тоді і тільки тоді, коли число його сотень, складене з потроєним числом десятків, кратне 23 (наприклад, 28842 ділиться на 23, так як 288 + (3·42)=414, продовжуємо 4

+ (3·14)=46 очевидно ділиться на 23)

ознака подільності на 25– число ділиться на 25 тоді і тільки тоді, коли дві його останні цифри діляться на 25 (тобто утворюють 00, 25, 50, 75) або

число кратне 5;

ознака подільності на 99– розіб’ємо число на групи по 2 цифри справа наліво(у самій лівій групі може бути одна цифра) і знайдемо суму цих груп, вважаючи їх двозначними числами. Ця сума ділиться на 99 тоді і тільки тоді, коли саме число ділиться на 99

ознака подільності на 101– розіб’ємо число на групи по 2 цифри справа наліво(у самій лівій групі може бути одна цифра) і знайдемо суму цих груп з змінними знаками, вважаючи їх двозначними числами. Ця сума ділиться на 101 тоді і тільки тоді, коли саме число ділиться на 101; (наприклад, 590547 ділиться на 101, так як 59-05+47 = 101)

Приклад 1. Перевірте, чи є 7 дільником числа 2002?

200 + 2·5 = 210, 210 націло ділиться на 7, отже і 2002 ділиться на 7.

Приклад 2. Перевірте, чи є 7 дільником числа 154?

15·3 + 4 = 49, 49 націло ділиться на 7, отже і 154 ділиться на 7.

Приклад 1. Перевірте, чи є 8 дільником числа 888124?

Тут багато хто бачить спереду 8 і думає, що ділиться, але давайте перевіримо правило: 124 : 2 = 62; 62 : 2 = 31; 31 : 2 = націло не ділиться. Бачимо, що на 4 число ділиться, а на 8 без остачі ніяк.

Задача 1. У книжковому магазині Мишко попросив у продавця стирачку за 3 гривні, кулькову ручку за 6 гривень , 3 пачки кольорових олівців і 11

зошитів, ціну яких він не знав. Продавець озвучує вартість всієї покупки, вона склала 54 гривні 40 копійок. Мишко заперечив, попросив перерахувати і виправити помилку.

Задача 2. Мама принесла дітям три однакових подарунка. Чи може бути, що у всіх подарунках було по 25 цукерок? 75 цукерок? 63 цукерки?

Задача 3. У кожному стійлі корівника 9 корів. Чи може бути, що всього у корівнику 542 корови? 288 корів?

Задача 4. Зібрали 2ц 2кг яблук і частина з них розклали в 4 однакових ящика. Чи могло після цього залишиться: 81кг яблук? 42кг яблук?

Задача 5. Не виконуючи ділення, довести, що число 7920 ділиться на 60.

Задача 6. Як можна 78 копійок маючи лише монети по три та п’ять копійок?

Друже! Впевнена, що мама колись неодмінно вчила Тебе: «Ніколи не грайся з сірниками!» Проте гра, яку я хочу Тобі запропонувати, цілком безпечна і навіть корисна. Вона обов’язково навчить Тебе знаходити нестандартні рішення непростих завдань.

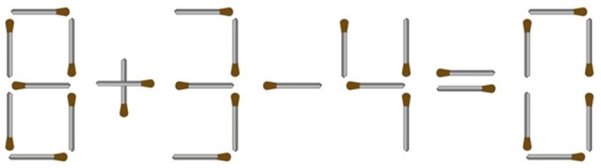
Уважно подивись на малюнок. Числа та математичні знаки на ньому складаються з сірників. На малюнку рівність не збережена. Та варто пересунути лише один сірник, щоб рівність стала правильною.

Цікаво, що це завдання має 4 варіанти вирішення. Два — правильні.

Одне — неточне.

1. Дванадцять сірників лежать так, як показано на малюнку. Скільки тут квадратів? Перекладіть 4 сірника так, щоб отримати 10 квадратів.

Вфдповідь:

2. Потрібно взяти всього вісім сірників і скласти з них два квадрати, вісім трикутників і один восьмикутник - і все це одночасно.

Відповідь:

3. На малюнку з сірників викладена невірна рівність 9+0=5. Перекладіть 1 сірник так, щоб рівність стала вірною.

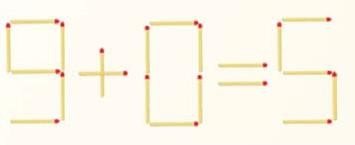
4. На малюнку з сірників викладена невірна рівність 2+2=8. Приберіть 2 сірники так, щоб рівність стала вірною.

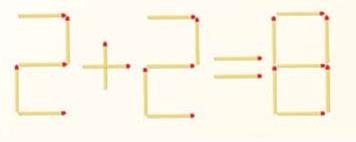
5. На малюнку з сірників викладена невірна рівність 5+19=15.

Перекладіть 1 сірник так, щоб рівність стала вірною.

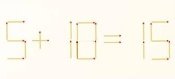Відповідь:

6. З сірників на малюнку викладена невірна рівність 5+9=6. Перекладіть 1 сірник так, щоб рівність стала вірною.

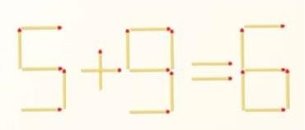
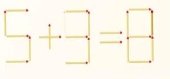Відповідь:

7. З сірників на малюнку викладена невірна рівність 20+14=5. Перекладіть 1 сірник так, щоб рівність стала вірною.

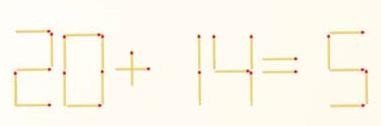
8. З сірників викладено число 2871. Перекладіть 2 сірники так, щоб отримати найменше з можливих чисел. (З нуля число починатися не може).

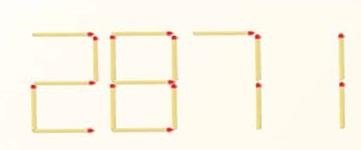
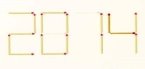Відповідь:

¨ популярні лекції з математики

¨ Математика он-лайн, занимательная математика -

школьникам

¨ Виртуальная школа юного математика

¨ Острів знань (математика)

http://www.ostriv.in.ua/index.php?option=com_menufolder&Itemid

=198&ft=1

¨ http://zaba.ru/ математические олимпиады и задачи.

¨ http://www.exponenta.ru/ - образовательный математический сайт

¨ http://kvant.mirror1.mccme.ru/ Науково-популярний фізико-математичний журнал "Квант"

¨ http://www.allmath.ru/ - математичний портал,

¨ http://www.mathtest.ru/ Математика для школярів

¨ http://www.man.gov.ua –Мала академія наук

¨ http://mathworld.ru/Даний веб-ресурс містить завдання, спрямовані на виховання гнучкості математичного мислення і розвиток ініціативи та кмітливості. На сайті ви також знайдете теоретичний матеріал з елементарної математики, цікаві математичні факти, історії з життя математиків

¨ http://math-on-line.com"Олімпіади, ігри, конкурси по математиці для школярів". Цікава математика - школярам. Он-лайн учбовий центр по проведенню олімпіад, ігор-тренінгів і конкурсів по математиці для школярів 5-8 класів

¨ http://www.golovolomka.hobby.ru/ Головоломки та парадокси.