Ленковецька сільська рада

Вербовецька загальноосвітня школа І-ІІ ступенів

 

                                              

Вчитель математики

   Конончук Т.М.

 

Великі математики

Навчальний посібник

 

 

 

 

 

 

Вербівці -2021

Конончук Т.М. Великі математики. Посібник. – Вербовецька загальноосвітня школа І-ІІ ступенів, 2021. –  109с.

 

В даному посібнику представлена інформація про видатних математиків, які внесли великий внесок у розвиток математики, як науки. Посібник містить також практичну частину, дані заходи можна використовувати під час проведення тижня математики. Посібник стане в пригоді для вчителів, а також для учнів.

Посібник містить ілюстрований матеріал

 

 

 

 

 

 

Рецензенти:

Миклащук О.В. – заступник директора з навчально-виховної роботи  Вербовецької загальноосвітньої школи І-ІІ ступенів

 

 

 

 

Рекомендовано засіданням методичної ради Вербовецької загальноосвітньої школи І-ІІ ступенів Ленковецької сільської ради Шепетівського району Хмельницької області ( протокол №4 від 24.02.2021)

 

 

 

 

 

 

 

 

 

 

Зміст

1. Вступ____________________________________________________________4

2. Вчені математики

 2.1 Фалес Мілетський________________________________________________6

 2.2 Піфагор________________________________________________________10

 2.3 Евклід_________________________________________________________24

 2.4 Архімед________________________________________________________27

 2.5 Франсуа Вієт___________________________________________________30

 2.6 Рене Декарт____________________________________________________34

 2.7 Ісаак Ньютон___________________________________________________38

 2.8 Блез Паскаль____________________________________________________42

 2.9 Вільгельм Лейбніц_______________________________________________45

 2.10 Леонард Ейлер_________________________________________________49

 2.11 Карл Фрідріх Гаусс_____________________________________________52

 2.12 Герон Александрійський_________________________________________56

 2.13 Микола Іванович Лобачевський___________________________________66

 2.14 Софія Василівна Ковалевська____________________________________70

 2.15 Андрій Миколайович Колмогоров_________________________________87

 2.16 Олексій Васильович Погорєлов___________________________________89

3. Практична частина

 3.1 Позакласний захід «Рене Декарт – людина та вчений»_________________91

 3.2 Математичний QR – квест_______________________________________103

 3.3 Вікторина : «Цікаві історії з життя видатних математиків»____________105

 3.4 Ребуси________________________________________________________106

4. Використані джерела_____________________________________________109

 

 

Передмова

« Життя прикрашають дві речі: моливість вивчати математику й можливість викладати її.»

 (С.Пуассон.)

 

      Впродовж багатьох століть люди з різних країн відкривали математику, уточнювали, вдосконалювали, поглиблювали відкрите і поширювали по всьому світу. У книжках, про які йдеться в цьому розділі, розповідається про історію відкриттів у математиці від найдавніших часів і до сьогодні.

Математика цікава і багатогранна наука.

На уроках викладач пояснює способи обчислення логарифмів, похідних, інтегралів, навчає учнів розв’язувати задачі, рівняння, доводити теореми. Але це лише сухі факти, за кожним з яких стоїть набагато більше: щасливі випадки й багаторічна завзята праця, провали й нескінченні експерименти багатьох вчених. Як і коли були зроблені найвагоміші відкриття в математиці, хто були їхні автори, – про все це можна дізнатись з посібника «Видатні математики давнини і сучасності».

В даний посібник входить хрестоматійний матеріал з математики, тобто відомості із життя математиків. Призначений для використання під час уроків, гуртків, факультативних занять, позаурочних математичних заходів.

В посібник входять цікаві факти із життя відомих математиків, починаючи із глибокої давнини, часу, коли математика лише розпочинала свій розвиток, і закінчуючи сьогоденням. Сюди ввійшли розповіді про тих математиків, іменами яких названі математичні теорії, теореми, формули, методи та інші математичні поняття, факти із життя вчених, які внесли значний вклад в розвиток математики, зокрема, алгебри і початків аналізу та геометрії, методики викладання математики, авторів підручників і навчальних посібників з різних розділів математики.

Зміст книги доповнює та забезпечує ілюстрацію програмного матеріалу з математики і стосується всього курсу математики та кожної теми зокрема.

Посібник створено не лише з навчальною а й з виховною метою. Він має духовно-ціннісний вплив на учня, формує науковий світогляд а саме знання про вчених, послідовно формує в учнів наукове, математичне мислення.

Даний посібник може бути використаний викладачами математики під час уроку: при вивченні будь-якої теми викладач може вибрати дані про вчених, які винаходили, досліджували ті чи інші поняття і у вигляді кількахвилинної бесіди донести історичні матеріали до учнів. Докладніше вивчення того чи іншого вченого можна розглянути на позакласному занятті з математики. Також дані матеріали можуть бути використані і учнями для написання рефератів про життя і діяльність окремих математиків.

 

 

 

 

 

 

 

 

 

 

 

Фалес Мілетський

(бл. 640 – 546 рр. до н.е.)

 

Учителів він не мав, якщо не враховувати того, що

Він їздив у Єгипет і жив там у жерців.

Діоген Лаертський

 

Фалес Мілетський – один із семи великих мудреців, йому приписують відкриття дедуктивної математики. Народився і жив Фалес в іонійському місті Мілеті на малоазійському узбережжі. На час життя Фалеса припадають соціальні революції в іонійських полісах. Поліси були невеликими країнами, які складалися з міста - столиці та прилеглих до нього земель. У процесі революційних переворотів політичну владу в рабовласницької родової аристократії забирала заможна олігархія, а іноді й рабовласницька демократія. Ці соціальні зрушення сприяли духовному і культурному розвитку  суспільства, одним із виявлень якого була діяльність самого Фалеса, родоначальника античної і європейської науки. Він був виключно обдарованим і різнобічним ученим – займався політикою, технікою, філософією, астрономією, математикою, торгівлею. Фалес, за переказами, був автором творів на природничі та філософські теми, але жодного рядка із них до нас не дійшло.

  Офіційних посад учений не займав, хоч прославився як політичний діяч своїми далекоглядними рекомендаціями з питань військової тактики. Як інженер Фалес відомий тим, що за його порадою для форсування річки провели канал, у який тимчасово відвели її русло. Воїни перейшли річку, не замочивши й ніг.

   Почесне місце Фалеса в історії філософії. Першоосновою всього він вважав матеріальне начало – воду, а це було справжньою революцією в поглядах на світобудову.

   Ім’я Фалеса стоїть першим і в історії математики. За даними більшості джерел родоначальники грецької науки свої наукові знання здобували, подорожуючи в Фінікію, Вавилон, Єгипет.

   Фалес займався вивченням фігури, яка утвориться, якщо в прямокутнику, вписаному в коло, провести діагоналі. При цьому він переконався, що кут, вписаний у півколо, завжди прямий. Це дало можливість вписувати в коло прямокутні трикутники і доводити теореми про суму внутрішніх кутів трикутника, а також про те, що кути можна додавати так само, як відстані.

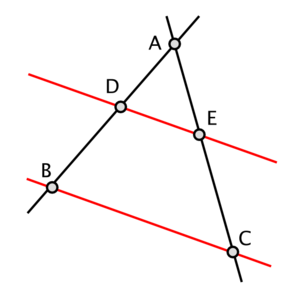
    Фалес самостійно обчислив висоту єгипетських пірамід за їхньою тінню, чим не мало здивував єгипетського фараона Амазіса. Він знайшов також розв’язання задачі на визначення відстані від корабля, що перебуває в морі, до гавані без безпосереднього вимірювання цієї відстані. Фалесу належить одна з найдавніших теорем з геометрії: « Якщо паралельні прямі, що перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки і на іншій стороні.»  

 У галузі астрономії Фалесу і його учням приписують визначення тривалості року (365 днів), думку про те, що Земля є серединою Всесвіту і має кулясту форму.

  Наукові дослідження у галузі математики, астрономії та інших наук Фалес поєднував із широкою державно-політичною діяльністю. Він був людиною високоосвіченою, мудрою й енергійною. Особливо цінними були його поради, що стосувалися військової справи.

    Гадають, що Фалес трагічно загинув на стадіоні під час великих олімпійських ігор, коли йому було майже 80 років. Про причини його загибелі існує кілька версій. Одна з них свідчить про те, що смерть сталася від сонячного удару, інша, що людський натовп, виходячи із стадіону, мимоволі заподіяв смерть старому мудрецеві. На пам’ятнику  Фалесу, що стоїть серед широких ланів, вирізьблено:   « Наскільки мала ця гробниця, настільки велика слава цього царя астрономії в галузі зірок».

   Зі славою і ім'ям Фалеса пов'язані показові історії

• Одного разу завантажений сіллю мул, переходячи убрід річку, раптово посковзнувся. Вміст тюків розчинилося, а тварина, піднявшись без нічого, зметикувало в чому справа, і з тих пір при переправі мул навмисно занурював мішки у воду, нахиляючись в обидві сторони. Почувши про це, Фалес велів наповнити мішки замість солі шерстю і губками. Навантажений ними мул спробував виконати старий трюк, але добився зворотного результату: поклажа стала значно важче. Кажуть, що надалі він переходив річку так обережно, що жодного разу не замочив вантаж навіть ненавмисно.

• Про Фалеса передавали таку легенду (її з великою охотою повторив Аристотель). Коли Фалеса, через його бідності, докоряли у марності філософії, він, зробивши по спостереження зірок висновок про прийдешній врожаї маслин, ще взимку найняв всі маслодавильних в Мілеті і на Хіосі. Найняв він їх за безцінь (бо ніхто не давав більше), а коли прийшла пора і попит на них раптово зріс, став віддавати їх в оренду на свій розсуд. Зібравши таким чином багато грошей, він показав, що філософи при бажанні легко можуть розбагатіти, але це не те, про що вони піклуються.Аристотель наголошує: урожай Фалес передбачив «зі спостереження зірок», тобто завдяки знанням.

• У шостий рік війни між лідійцями і мідянами сталося битва, під час якого «день раптово став вночі ». Це було те саме сонячне затемнення 585 до н. е.., «завчасно» передбачене Фалесом і сталося саме в передбачений термін. Лідійці і мідяни були настільки вражені і перелякані, що припинили битву і поспішили укласти мир.

Іменем Фалеса названа геометрична теорема.

Теорема Фалеса : 

Вважається, що Фалес першим сформулював і довів кілька геометричних теорем, а саме:

• вертикальні кути рівні;
• має місце рівність трикутників по одній стороні і двом прилеглим до неї кутам;
• кути при основі рівнобедреного трикутника рівні;
• діаметр ділить коло навпіл;
• вписаний кут, що спирається на діаметр, є прямим.

Фалес навчився визначати відстань від берега до корабля, для чого використовував подобу трикутників. В основі цього методу лежить теорема, названа згодом теоремою Фалеса: якщо паралельні прямі, які перетинають сторони кута, відтинають рівні відрізки на одній його стороні, то вони відсікають рівні відрізки і на іншій його стороні.

Легенда розповідає про те, що Фалес, будучи в Єгипті, вразив фараона Амасіса тим, що зумів точно встановити висоту піраміди, дочекавшись моменту, коли довжина тіні палиці стає рівною її висоті, і тоді виміряв довжину тіні піраміди.

Піфагор

 ( бл. 585 – 500 рр. до н. е. )

Заслугою перших грецьких математиків, таких, як Фалес,

 Піфагор і піфагорійці, є не відкриття математики,

 а її систематизація і обґрунтування. В їхніх руках

 обчислювальні рецепти, що ґрунтуються на неясних

уявленнях, перетворилися в точну науку.

                                               Б. Ван  дер Варден

 

Народився Піфагор на о. Самосі, біля узбережжя Малої Азії. Його батько Мнесарх із знатного, але збіднілого роду, був каменерізом. Як і інші великі греки, Піфагор здійснив традиційну подорож до Єгипту, де жив близько 22 років і витримав немало випробувань, перш ніж жерці Мемфіса і Діосполіса відкрили йому «дивовижне чергування чисел, хитромудрі правила геометрії, науку про зорі, медицину». До вавилонських магів і халдеїв він потрапив проти своєї волі – як полонений перського царя Камбуза, який завоював на той час Єгипет. Дванадцять років Піфагор перебував у полоні, поки його не звільнив перський цар Дарій Гістасп, що почув про уславленого грека. Піфагору на той час уже виповнилось шістдесят років. Він вирішив повернутися на батьківщину, щоб прилучити до накопичених знань свій народ, створивши у Кротоні власну філософську школу. Незабаром навколо Піфагора згуртувалися однодумці, організувавши аристократичний за духом, таємний релігійно-політичний союз – гетерію. Незабаром і в інших полісах південної Італії та Греції виникли піфагорійські гетерії, в яких поряд із науковими проблемами – математичними, філософськими, етичними – розглядалися релігійні й політичні.

У школі Піфагора вперше було висловлено здогад про кулястість Землі. Слід також завважити, що вчений уявляв Землю кулею, що обертається навколо Сонця. Багато чого зробив учений і в геометрії. Саме у школі Піфагора геометрія вперше оформилась в самостійну наукову дисципліну. Піфагор та його учні першими стали вивчати геометрію системно – як теоретичне вчення про властивості абстрактних геометричних фігур, а не як збірник прикладних ілюстрацій в галузі до землеробства.

Найважливішою науковою заслугою Піфагора вважається те, що він системно ввів доведення в математику і, насамперед, у геометрію. Власне кажучи, тільки з цього моменту математика й починає існувати як наука. З народженням же математики зароджується й наука взагалі, бо «жодне людське дослідження не може називатися справжньою наукою, якщо воно не пройшло через математичні доведення», як казав Леонардо да Вінчі.

Отже, заслуга Піфагора й полягала в тому, що він, очевидно, першим прийшов до такої думки: геометрія, по-перше, повинна розглядати абстрактні ідеальні об’єкти і, по-друге, властивості цих об’єктів мають встановлюватися не за допомогою вимірів з обмеженою кількістю об’єктів, а за допомогою міркувань, справедливих для нескінченної кількості об’єктів. Цей ланцюжок міркувань, що за допомогою законів логіки зводить неочевидні твердження до відомих або очевидних істин, і є математичним доведенням.

Піфагор заснував школу, розквіт якої припадає на період близько 550 – 300 років до нашої ери. Піфагорійці створили чисту математику у формі теорії чисел і геометрії. Цілі числа вони подавали у вигляді конфігурацій із крапок або камінців, класифікуючи ці числа відповідно до форми фігур , що виникали. Із простих геометричних конфігурацій виникали певні властивості цілих чисел. Наприклад, піфагорійці відкрили, що сума двох послідовних трикутних чисел завжди дорівнює певному квадратному числу. Саме піфагорійцям ми  багато в чому завдячуємо тією математикою, що потім була систематизовано викладена й доведена в Началах Евкліда. Є підстави думати, що саме вони відкрили те, що нині  відомо як теореми про трикутники, паралельні прямі, багатокутники, кола, сфери і правильні багатогранники.

Стародавні греки розв’язували рівняння із невідомими за допомогою геометричних побудов. Були розроблені спеціальні побудови для виконання додавання, віднімання, множення й поділу відрізків, добування квадратного кореня із довжин відрізків; нині цей метод називається геометричною алгеброю.

Приведення задач до геометричного вигляду мало ряд важливих наслідків. Зокрема, числа стали розглядатися окремо від геометрії. Геометрія стала основою майже всієї строгої математики принаймні до 1600 року.

За теоремою Піфагора сума площ квадратів, побудованих  на катетах  прямокутного трикутника, дорівнює площі  квадрата, побудованого на гіпотенузі.

      Це одна з найвідоміших геометричних теорем давнину, звана теоремою Піфагора. Її і зараз знають практично всі, хто коли-небудь вивчав планіметрію. Нам здається, що якщо ми хочемо дати знати позаземним цивілізаціям про існування розумного життя на Землі, то слід посилати в космос зображення Піфагора фігури. Думається, що якщо цю інформацію зможуть взяти мислячі істоти, то вони без складної дешифрування сигналу зрозуміють, що на Землі існує досить розвинена цивілізація.

Сьогодні прийнято вважати, що Піфагор дав перший доказ носить його ім'я теореми. На жаль, від цього докази також не збереглося ніяких слідів. Тому нам нічого не залишається, як розглянути деякі класичні докази теореми Піфагора, відомі з давніх трактатів. Зробити це корисно ще й тому, що в сучасних шкільних підручниках дається алгебраїчне доказ теореми. При цьому безслідно зникає первозданна геометрична аура теореми, втрачається та нитка Аріадни, яка вела древніх мудреців до істини, а шлях цей майже завжди опинявся найкоротшим і завжди красивим ».
Теорема Піфагора говорить: «Квадрат, побудований на гіпотенузі прямокутного трикутника, рівновеликий сумі квадратів, побудованих на його катетах». Найпростіше доведення теореми виходить в найпростішому випадку рівнобедреного прямокутного трикутника. Ймовірно, з нього і починалася теорема. У насправді, досить просто подивитися на мозаїку рівнобедрених прямокутних трикутників, щоб переконатися в справедливості теореми.

Доведення методом розкладу

Існує цілий ряд доказів теореми Піфагора, в яких квадрати, побудовані на катетах і на гіпотенузі, розрізають так, що кожної частини квадрата, побудованого на гіпотенузі, відповідає частина одного з квадратів, побудованих на катетах. У всіх цих випадках для розуміння докази достатньо одного погляду на креслення; міркування тут може бути обмежене єдиним словом: "Дивись!", Як це робилося в творах стародавніх індуських математиків. Слід, однак, зауважити, що насправді доказ можна вважати повним, поки ми не довели рівності всіх відповідних один одному частин. Це майже завжди досить важко зробити, однак може (особливо при великій кількості частин) зажадати досить тривалої роботи.

Доведення Епштейна

Почнемо з докази Епштейна (рис.1); його перевагою є те, що тут в якості складових частин розкладання фігурують виключно трикутники. Щоб розібратися в кресленні, зауважимо, що пряма CD проведена перпендикулярно прямий EF.
Розкладання на трикутники можна зробити і більш наочним, ніж на малюнку.
                                              Доведення Нільсена

На малюнку допоміжні лінії змінені за пропозицією Нільсена.

Доведення Бетхера

На малюнку дано досить наочне розкладання Бетхер.

Доведення Перігаля

У підручниках нерідко зустрічається розкладання зазначене на малюнку (так зване "колесо з лопатями"; це доказ знайшов Перігаль). Через центр O квадрата, побудованого на більшій катета, проводимо прямі, паралельну і перпендикулярну гіпотенузі. Відповідність частин фігури добре видно з креслення.

Доведення Гутхейля

Зображене на малюнку розкладання належить Гутхейль; для нього характерне наочне розташування окремих частин, що дозволяє відразу побачити, які спрощення спричинить за собою випадок рівнобедреного прямокутного трикутника.

Доведення 9 століття н.е.

 

 

Раніше були представлені тільки такі докази, в яких квадрат, побудований на гіпотенузі, з одного боку, і квадрати, побудовані на катетах, з іншого, складалися з рівних частин. Такі докази називаються доказами за допомогою додавання ("адитивними доказами") або, частіше, доказами методом розкладання. До цих пір ми виходили з звичайного розташування квадратів, побудованих на відповідних сторонах трикутника, тобто поза трикутника. Однак у багатьох випадках більш вигідно інше розташування квадратів.

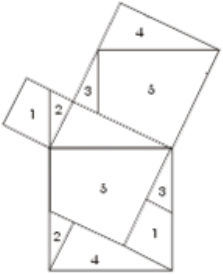
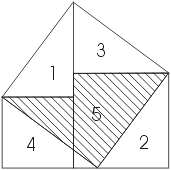
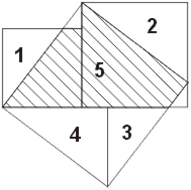
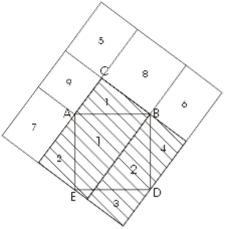
На малюнку квадрати, побудовані на катетах, розміщені ступенями один поруч з іншим. Цю фігуру, яка зустрічається в доказах, що датуються не пізніше, ніж 9 століттям н. е.., індуси називали "стільцем нареченої". Спосіб побудови квадрата зі стороною, рівною гіпотенузі, ясний з креслення. Загальна частина двох квадратів, побудованих на катетах, і квадрата, побудованого на гіпотенузі, - неправильний заштрихований п'ятикутник 5.
Приєднавши до нього трикутники 1 і 2, отримаємо обидва квадрата, побудовані на катетах; якщо ж замінити трикутники 1 і 2 рівними їм трикутниками 3 і 4, то отримаємо квадрат, побудований на гіпотенузі. На малюнках нижче зображено два різних розташування близьких до того, яке дається на першому малюнку.

Доведення методом доповнення

Поряд з доказами методом складання можна навести приклади доказів при допомозі віднімання, званих також доказами методом доповнення. Загальна ідея таких доказів полягає в наступному.
Від двох рівних площ потрібно відняти рівновеликі частини так, щоб в одному випадку залишилися два квадрати, побудовані на катетах, а в іншому-квадрат, побудований на гіпотенузі. Адже якщо в рівностях
В-А = С і В1-А1 = С1
частина А рівновелика частини А1, а частина В рівновелика В1, то частини С і С1 також рівновеликі.
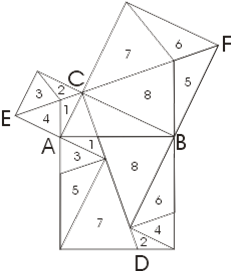
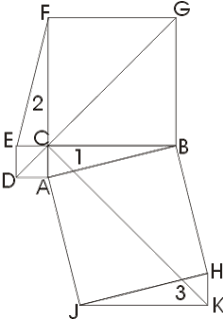
Пояснимо цей метод на прикладі. На рис. до звичайної Піфагора фігурі приставлені зверху і знизу трикутники 2 і 3, рівні вихідного трикутника 1. Пряма DG обов'язково пройде через C. Зауважимо тепер (далі ми це доведемо), що шестикутники DABGFE і CAJKHB рівновеликі. Якщо ми від першого з них віднімемо трикутники 1 і 2, то залишаться квадрати, побудовані на катетах, а якщо від другого шестикутника віднімемо рівні трикутники 1 і 3, то залишиться квадрат, побудований на гіпотенузі. Звідси випливає, що квадрат, побудований на гіпотенузі, рівновеликий сумі квадратів, побудованих на катетах.
Залишається довести, що наші шестикутники рівновеликі. Зауважимо, що пряма DG ділить верхній шестикутник на рівновеликі частини; те саме можна сказати про прямий CK і нижньому шестикутнику. Повернемо чотирикутник DABG, що становить половину шестикутника DABGFE, навколо точки А за годинниковою стрілкою на кут 90; тоді він співпаде з чотирикутником CAJK, складовим половину шестикутника CAJKHB. Тому шестикутники DABGFE і CAJKHB рівновеликі.

Доведення методом віднімання

Познайомимося з іншим доказом методом віднімання. Знайомий нам креслення теореми Піфагора укладемо в прямокутну рамку, напрямки сторін якої збігаються з напрямками катетів трикутника. Продовжимо деякі з відрізків фігури так, як вказано на малюнку, при цьому прямокутник розпадається на кілька трикутників, прямокутників і квадратів. Викинемо з прямокутника спочатку кілька частин так щоб залишився лише квадрат, побудований на гіпотенузі. Ці частини наступні:
трикутники 1, 2, 3, 4;
прямокутник 5;
прямокутник 6 і квадрат 8;
прямокутник 7 і квадрат 9;
Потім викинемо з прямокутника частини так, щоб залишилися тільки квадрати, побудовані на катетах. Цими частинами будуть:
прямокутники 6 і 7;
прямокутник 5;
прямокутник 1 (заштрихований);
прямокутник 2 (заштрихований);
Нам залишилося лише показати, що відібрані частини рівновеликі. Це легко бачити в силу розташування фігур. З малюнка ясно, що:
прямокутник 5 рівновеликий самому собі;
чотири трикутника 1,2,3,4 рівновеликі двом прямокутникам 6 і 7;
прямокутник 6 і квадрат 8, взяті разом, рівновеликі прямокутнику 1 (заштрихований);;
прямокутник 7 разом з квадратом 9 рівновеликі прямокутнику 2 (заштрихований);
доказ закінчено.

Спрощене доведення Евкліда

Як в доказах методом розкладання, так і при доказі евклідової типу можна виходити з будь-якого розташування квадратів. Іноді при цьому вдається досягти спрощень.
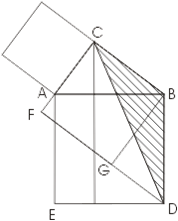
Нехай квадрат, побудований на одному з катетів (на малюнку це квадрат, побудований на більшій катета), розташований з тієї ж сторони катета, що і сам трикутник. Тоді продовження протилежної катету сторони цього квадрата проходить через вершину квадрата, побудованого на гіпотенузі. Доказ в цьому випадку виявляється зовсім простим, тому що тут досить порівняти площі цікавлять нас фігур з площею одного трикутника (він заштрихований) - площа цього трикутника дорівнює половині площі квадрата і одночасно половині площі прямокутника.

 

Доведення Хоукінса

Наведемо ще один доказ, яке має обчислювальний характер, проте сильно відрізняється від всіх попередніх. Воно опубліковане англійцем Хоукінсом у 1909 році; чи було воно відомо до цього-важко сказати.

Прямокутний трикутник ABC з прямим кутом C повернемо на 90 ° так, щоб він зайняв положення A'CB '. Продовжимо гіпотенузу A'В 'за точку A' до перетину з лінією АВ в точці D. Відрізок В'D буде висотою трикутника В'АВ. Розглянемо тепер заштрихований чотирикутник A'АВ'В. Його можна розкласти на два рівнобедрених трикутника САA 'і СВВ' (або на два трикутники A'В'А і A'В'В).

SCAA '= b ² / 2

SCBB '= a ² / 2

SA'AB'B = (a ² + b ²) / 2

Трикутники A'В'А і A'В'В мають загальну підставу з і висоти DA і DB, тому:

SA'AB'B = c * DA / 2 + c * DB / 2 = c (DA + DB) / 2 = c ² / 2

Порівнюючи два отриманих вирази для площі, отримаємо:

a ² + b ² = c ²

Теорема доведена.

 

Основне доведення методом подібності

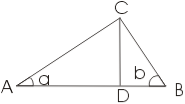
У прямокутному трикутника АВС проведемо з вершини прямого кута висоту CD; тоді трикутник розіб'ється на два трикутники, які також є прямокутними. Отримані трикутники будуть подібні один одному і вихідного трикутника. Це легко довести, користуючись першою ознакою подібності (по двох кутах). У самому справі, відразу видно що, крім прямого кута, трикутники АВС і ACD мають загальний кут a, трикутники CBD і АВС - загальний кут b. Те, що малі трикутники також подібні один одному, випливає з того, що кожен з них подібний до великого трикутника. Втім, це можна встановити і безпосередньо.

Інші доведення теореми Піфагора

Докази, засновані на використанні поняття равновеликости фігур.

Адитивні докази.

Доведення методом добудованих

Алгебраїчний метод докази.

Доказ Вальдхейма.

 

Існує багато доказів теореми Піфагора, проведених як кожним з описаних методів, так і за допомогою поєднання різних методів.

Коли Піфагор зробив необхідні обчислення своєї  теореми, він одержав дивний результат: співвідношення діагоналі квадрата до його сторони не може дорівнювати ніякому дробу! Піфагор був вражений. Виходить, навіть серед ідеальних тіл геометрії не існує повної гармонії! Він вирішив, що цей факт слід приховати від невігласів до тих пір, поки знавці до кінця збагнуть гармонію математичного світу! Так і було зроблено. Тому вчення Піфагора не відбилося ні в якій книзі, а передавалося з вуст у вуста – з суворою забороною говорити відверто з чужинцями.

 

 

 

 

Евклід

( бл. 365 – бл. 300 рр. до н. е.)

 Твір Евкліда житиме ще довго після того,

як усі підручники наших днів буде замінено

іншими й забуто. Це одна з найпрекрасніших

пам’яток античності.

                                           Т. Хізс

Історія не зберегла для нас достовірних відомостей про життя цього видатного вченого. Вважають, що Евклід народився в Афінах близько 365 р. до н. е. і на запрошення царя Птоломея І на початку ІІІ ст.. до н. е. прибув до Александрії. В одному із своїх творів математик Папп, що жив в Александрії в ІІІ – IV ст.. до н. е. зображає Евкліда як людину виключно чесну, тиху і скромну, якій були чужими гордість і егоїзм. Працюючи в бібліотеці Музейону над упорядкуванням математичних манускриптів, Евклід створив славнозвісну працю з математики, яку назвав «Начала». Наскільки серйозно він відносився до вивчення математики можна судити із наступної розповіді Прокла: цар Птоломей запитав Евкліда, чи не можна знайти коротший і легший шлях до  вивчення геометрії, ніж його «Начала». Евклід відповів: « Не має царської дороги в геометрії!»

Свій твір Евклід почав з визначення таких термінів, як пряма, кут і коло. «Начала» Евкліда складаються з 13 «книг»-сувоїв. Перші шість книг присвячені планіметрії, VII – X книги – арифметиці та несумірним величинам, які можна побудувати за допомогою циркуля і лінійки, XI – XIII – стереометрії. Перша книга починається викладом 23 означень і 10 аксіом, причому перші п’ять із цих аксіом називаються «загальними поняттями», а решта – «постулатами» ( у різних списках «Начал» є різні кількості аксіом і постулатів ). Формулюючи постулати, Евклід користується співвідношеннями рівності, які означаються «загальними поняттями»  – аксіомами. Під розв’язуванням задач Евклід розумів побудову за допомогою циркуля та лінійки. Зокрема, для Евкліда знайти площу або об’єм означало побудувати циркулем і лінійкою квадрат чи куб потрібної площі або об’єму.

«Начала» Евкліда закінчувалися побудовою за допомогою циркуля і лінійки ребер п’яти правильних многогранників, вписаних у сферу даного радіуса, і дослідженням здобутих несумірних величин.

Видатний учений подолав неабиякі труднощі, щоб систематизувати, узагальнити та довести багато складних співвідношень між елементами просторових і плоских фігур, які виражаються деякими числами. У той час ще не було не тільки буквеної символіки, а навіть знаків дій додавання, віднімання тощо. Усе записували словами та зображували геометричними малюнками. Тепер, користуючись запровадженою в XVI – XVIIст. буквеною символікою, ми швидко і легко виводимо найрізноманітніші формули, які виражають залежності між різними, у тому числі й геометричними величинами.

Для математиків текст евклідових «Начал» тривалий час був зразком чіткості. Знаменита книга «Начал» є першою й найкращою енциклопедією елементарної математики. Двадцять століть геометрію вивчали саме за цією книгою, перш ніж у неї з’явилися гідні суперниці – праці Гауса і Лобачевського, Болья й Ріманна. Та все одно геометрія, що її вивчають у школі, називається іменем видатного вченого – евклідовою.

Цікаво, що Евклід у своїй енциклопедії описав лише дві різні лінії – пряму і коло. Але в його епоху вже були відомі еліпс, парабола й гіпербола. Сам Евклід вивчав ці криві, навіть написав про них окрему книгу (яка не збереглася, але стала основою для подібної книги Аполлонія). Чому він жодним словом не згадав про нові криві в «Началах»? Мабуть, тому, що Евклід і його сучасники не знали про ці лінії всього, що їм хотілося знати. Наприклад, як обчислити площу, обмежену еліпсом або параболою? Як провести дотичну до еліпса або гіперболи в даній точці? Це зумів зробити тільки Архімед – через піввіку після Евкліда. Автор «Начал « цього не зумів – і вирішив за краще промовчати про складні криві, щоб не бентежити уми новачків-геометрів необґрунтованими міркуваннями. Напевно, Евклід мав рацію: так само роблять автори сучасних підручників.

Інакше стояла справа з арифметикою: тут Евклід сам був першовідкривачем. Саме тут він зробив три значних відкриття:

        Сформулював (без доведення) теорему про ділення з залишком.

        Створив «алгоритм Евкліда» – швидкий спосіб знаходження найбільшого загального дільника чисел або загальної міри відрізків .

        Евклід перший почав вивчати властивості простих чисел і довів, що їхня множина нескінченна.

 Величезне значення діяльності Евкліда у тому, що він підсумував і узагальнив усі попередні досягнення грецької математики і створив фундамент для її подальшого розвитку. Історики вважають, що «Начала» – це обробка творів попередніх грецьких математиків X – IV ст. до н. е. історичне значення «Начал» Евкліда полягає в тому, що це була перша наукова праця, в якій зроблено спробу дати аксіоматичну побудову геометрії. Жодна наукова праця не мала такого великого успіху, як «Начала» Евкліда. З 1482 р. «Начала» витримали понад 500 видань багатьма мовами світу.  

Архімед

( бл. 287 – 212 рр. до н.е. )

 

 Грецька математика «вічна», навіть більш вічна,

 ніж грецька література. Архімеда пам’ятатимуть,

коли Есхіла забудуть, бо мови вмирають, а математичні ідеї – ні.

                                                                        Г. Харді

 

 

 

 

 

 

 

 

 

Народився Архімед близько 287 року до н. е. в Сіракузах на острові Сіцілія. Здобувши освіту в свого батька – астронома і математика Фідія, Архімед переїхав до Александрії удосконалювати свої знання з математики й астрономії. Тут він зблизився з учнями Евкліда – математиком Ератосфеном, астрономом Кононом і Досіфеєм. Повернувшись до Сіракуз, Архімед підтримував зв’язки з цими вченими. Частина його праць дійшла до нас у вигляді листів до видатних математиків.

Генія в науці можна розпізнати за тим, як швидко він осягає досягнення попередників і як нестримно починає рухатись вперед із цього стартового рубежу. Для Архімеда стартовими опорами стали Евклід і Евдокс.

Наукова діяльність Архімеда була пов’язана з життєвими потребами його батьківщини. Учений проводив дослідження у галузі математики, фізики, механіки, астрономії. За переказами, він так захоплювався наукою, що забував навіть про їжу. Архімед був також видатним інженером – винахідником і брав безпосередню участь у підготовці оборонних споруд. Під час другої Пунічної війни він керував обороною рідного міста. Війна велась між римлянами карфагенянами (пунами), грецькі Сіракузи виступали на боці карфагенян. Коли римське військо почало наступ з моря і суші, Архімед привів у дію сконструйовані ним метальні машини. На сухопутне військо з великою силою і швидкістю посипалось каміння. Цілі підрозділи ворогів падали на землю, руйнуючи свої бойові порядки. Водночас у море полетіли з кріпосних стін важкі балки, зігнуті у вигляді рогів. Від їхніх сильних ударів кораблі йшли на дно. Великі гаки, піднімали кораблі високо в повітря і кидали їх кормою в море або на скелі біля стін міста. Римське військо було дуже налякане. Побачивши над стіною міста якусь палицю або канат, воїни кричали: «Ось, ось воно!» і з жахом розбігалися.

Восени  212 р., коли римляни нарешті оволоділи Сіракузами, Архімед трагічно загинув. Давньогрецький письменник Плутарх розповідав, що Архімед сидів, розмірковуючи над якоюсь геометричною фігурою, коли перед ним з’явився римський солдат і зажадав, щоб він пішов із ним до Марцелла (воєначальника). Але вчений відповів, що піде лише тоді, коли розв’яже задачу. Солдат обурився, вихопив меч і вбив Архімеда. Є й інші версії смерті видатного математика і механіка.

Мабуть, найпершим твором Архімеда був твір «Начала», в якому він виклав свої міркування про обчислення і лічбу. Незважаючи на незручний запис чисел, Архімед упевнено підсумував послідовності натуральних чисел, їхніх квадратів і кубів. Використовуючи ці суми й не знаючи таких понять « з майбутнього », як багаточлен та інтеграл, Архімед, по суті справи, інтегрував багаточлени – і жодного разу не помилився в цій роботі! Спочатку він обчислив площу фігури, обмеженої відрізками параболи й прямої. Потім були знайдені об’єми тіл, отриманих при обертанні цієї фігури навколо різних осей; за цими даними Архімед знайшов центр ваги плоскої фігури.

Архімед сформулював багато теорем про площі й об’єми складних фігур і тіл, які він цілком строго довів методом вичерпування. Архімед завжди прагнув одержати точні рішення й знаходив верхні й нижні оцінки для ірраціональних чисел. Архімед довів також кілька теорем, що містили нові результати геометричної алгебри. Йому належить формулювання задачі про розсічення кулі площиною так, щоб об’єми сегментів перебували між собою в заданому відношенні.

Про свої відкриття Архімед писав математикові Досіфею: «Я довів, що поверхня всякої кулі в чотири рази більша від площі її великого круга, що об’єм циліндра, основа якого дорівнює площі великого круга кулі, а висота – діаметру кулі, в півтора рази більший від об’єму цієї кулі, а його поверхня (включаючи і площі основ) у півтора рази більша від поверхні кулі; піраміда дорівнює третині призми, якщо вони мають рівні основи і висоти, а конус – третині циліндра (про конус знав і Евдокс).Зрозуміло, що ці властивості тіла мали завжди, але видатні геометри, які жили до Евдокса, не знали цих властивостей і ніхто з них не відкрив їх». Ці відкриття Архімед вважав дуже важливими і висловлював бажання, щоб на могилі встановили пам’ятник, на якому був би зображений циліндр із вписаною в нього кулею.

Архімед був найвидатнішим математичним фізиком стародавності. Для доведення теорем механіки він використовував геометричні міркування. Особливо важливий його твір «Про плаваючі тіла», що заклав основи гідростатики. Згідно першого закону гідростатики, на всяке тіло, занурене у рідину, діє виштовхувальна сила, яка дорівнює вазі витисненої рідини. Відповідно до легенди, цей закон, який був названий його ім’ям, Архімед відкрив під час купання. Від радості, що його охопила, він вибіг на вулицю з вигуком: «Еврика!» ( «Знайшов!») 

 

 

 

Франсуа Вієт

( 1540 – 1603 рр. )

 

…він задовольнявся тим, що служив своїй

батьківщині на другорядних посадах і в пізнішому віці

взявся за математику за покликанням. Незважаючи на

це, він займає становище найвидатнішого математика

кінця шістнадцятого століття…

                                                    Д. Сміт

 

Франсуа Вієт – видатний французький математик, «батько алгебри», народився в місті Фонтеней. По професії юрист. Зацікавившись астрономією, Вієт повинен був зайнятися тригонометрією і алгеброю. Його праці з математики були написані важкодоступною мовою і тому не отримали відповідного поширення. Праці Вієта були зібрані після його смерті професором математики в Лейдені Ф. Шоотеном і видані в 1646 році в Лейдені Галіусом, М. Мерсенном та О. Андерсеном під заголовком «Opera Vietal».

Вієт розпочав систематичне використання літер для позначення невідомих і постійних величин. Це нововведення дало йому змогу знайти єдиний метод розв’язання рівнянь другого , третього й четвертого степенів. Тим самим він впровадив у науку визначну ідею про можливість виконувати алгебричні перетворення над символами, тобто ввести поняття математичної формули. Цим він вніс вирішальний вклад у створення буквеної алгебри, чим завершив розвиток математики епохи Відродження й підготував грунт для появи досягнень Ферма, Декарта, Ньютона.

У 1584 році у відповідь на настійну вимогу герцогів де Гізів Вієта відсторонили від посади і вислали з Парижа. Саме на цей період припадає пік його наукових досягнень. Учений поставив собі за мету створення всеохоплюючої математики, що дає змогу розв’язувати будь-які задачі. Він був переконаний у тому, «що повинна існувати загальна, невідома ще наука, що охоплює і дотепні побудови новітніх алгебристів, і глибокі геометричні пошуки давніх».

Вієт виклав програму своїх досліджень у трактатах, об’єднаних загальним задумом і написаних математичною мовою нової буквеної алгебри, та у виданому в 1591 році знаменитому «Введенні в аналітичне мистецтво», що разом мали скласти новий напрямок у науці. На жаль, цього не сталося. Однак головний задум ученого здійснився: почалося перетворення алгебри на потужне математичне обчислення. Саму назву «алгебра» Вієт у своїх працях замінив словами «аналітичне мистецтво». Вієт показав, що, оперуючи із символами, можна одержати результат, застосовуваний до будь-яких відповідних величин, тобто розв’язати задачу в загальному вигляді. Це поклало початок докорінному перелому в розвитку алгебри: стало можливим буквене обчислення. Він першим став застосовувати дужки, які, щоправда, в нього мали вигляд не дужок, а риски над багаточленом.

Символіка Вієта дала також змогу розв’язувати й конкретні задачі, й знаходити загальні закономірності, повністю обґрунтовуючи їх. Таким чином, алгебра відокремилась в самостійну галузь математики, що не залежить від геометрії. Від Вієта нам залишились й формули для обчислення коренів квадратних рівнянь, які мають назву теореми Вієта. В працях Вієта елементарна алгебра прийняла майже закінчений сучасний вигляд (за виключенням логарифмів, комбінаторики та бінома Ньютона, введених в курс елементарної алгебри пізніше).

Цікаво, що Вієт розпочав свою кар’єру як адвокат, а згодом був секретарем і вчителем доньки хазяїна у знатній гугенотській родині де Партене. Саме завдяки викладанню прокинулась цікавість молодого юриста до математики. В 1571 році Вієт перейшов на державну службу, ставши радником парламенту, а потім радником короля Франції Генріха III. У 1580 році Генріх ІІІ призначив Вієта на важливий державний пост, що надавав право контролювати від імені короля виконання розпоряджень у країні й скасовувати накази великих феодалів. Перебуваючи на державній службі, Вієт залишався вченим. Він зажив слави тим, що знайшов ключ до шифру, який використовували іспанці під час війни з Францією і навіть знайшов спосіб слідкувати за всіма змінами цього шифру.

Ім'ям Вієта і названа теорема, яка звучить так: сума коренів зведеного квадратного рівняння дорівнює другому коефіцієнту, взятого з протилежним знаком. А їх добуток – вільному члену.

Теорема Вієта дозволяє вгадувати цілі корені квадратного тричлена. Так, знаходячи корені квадратного рівняння x²– 5x + 6 = 0, можна почати з того, щоб спробувати розкласти вільний член (число 6) на два множника так, щоб їх сума дорівнювала б числу 5. Це розкладання очевидно:
6 = 2 ∙ 3, 2 + 3 = 5. Звідси має випливати, що числа 2 і 3 є шуканими коренями.
Приклад. Розв’язати рівняння х² – 8х + 12 = 0.
Нехай х₁ , х₂ - його корені. За теоремою Вієта х₁ ∙ х₂ = 12. Розкласти число 12 на два співмножники можна трьома способами: 12 ∙ 1; 6 ∙ 2; 4 ∙ 3. Вибираємо ту пару чисел, яка в сумі дає число 8. Отже, числа 6 і 2 задовольняють обидві вимоги теореми: 6 ∙ 2 = 12 і 6 + 2 = 8 і є розв’язками рівняння х² – 8х + 12 = 0.

Застосування теореми Вієта для розв’язування квадратних рівнянь з дробовими коренями.

Розглянемо рівняння 2х² – 8х – 90 = 0. Зазвичай ми вирішуємо таке рівняння за допомогою дискримінанту. Але його можна вирішити простіше: сума коренів буде така ж, як у зведеному (— b), а добуток c множиться на а. Але тоді ми множимо корені на а: 2х₁ + х₂ = 8,
2х₁ ∙ х₂ = – 180;

         2х₁ = 18,
2х₂ = – 10;
х₁ = 9,
         х₂ = – 5
Приклад.
Розв’язати рівняння 2х² – 7х + 3 = 0.
Щоб знайти розв’язки, розкладемо на два співмножники не вільний член 3, а добуток першого коефіцієнта 2 на вільний член 3, а добуток першого коефіцієнта 2 на вільний член 3, тобто число 6, так щоб сума дорівнювала числу 7 (коефіцієнту при х, взятому зі знаком мінус).
6 = 6 ∙ 1 і 6 + 1 = 7.

Знайдені числа 6 і 1 ділимо на коефіцієнт при х² і дістаємо х = 3 і 0,5 - розв’язки рівняння.
 

 

 

 

 

Рене Декарт

(1596 – 1650 рр.)

 

Велика справа Декарта – створення

аналітичної геометрії – перекинула міст

між алгеброю і геометрією.

                                С.І. Вавилов

 

 

 

 

 

 

 

 

Рене Декарт – французький філософ, математик, фізик, фізіолог. Народився 31 березня 1596 року в містечку Лае в дворянській сім’ї . В 8 років Декарт  поступив в аристократичний коледж (середній навчальний заклад) в Ла-Флеш, який закінчив в 1612 році і почав готуватися до військової кар’єри. Зустріч зі шкільним товаришем М. Мерсенном змінює плани Декарта. Він посилено займається науками, більше всього математикою, яка захоплювала його достовірністю своїх висновків.

Ще в коледжі Декарт зневажав схоластику і догматику, але цікавився географією, математикою. Ось що пізніше писав сам Декарт: «Як тільки вік мені дозволив не підкорятися більше своїм наставникам, я перестав вивчати науки і вирішив не шукати нової науки, крім тієї, яку міг би придбати в самому собі і в великій книзі природи. Я використав молоді роки на те, щоб подорожувати, вивчати людей з різними характерами і статусами…»  Бажаючи здійснити давню мрію про тривалі подорожі, Декарт поступає в 1618 році голландську армію і приймає участь в тридцятирічній війні. Він подорожував по Нідерландам та Італії і, закінчивши військову службу, пробув деякий час в Парижі. Декарт, як і багато інших новаторів науки, піддавався жорстоким переслідуванням в Франції. От чому він в 1629 році переселяється в Голландію, саму прогресивну країну того часу.

В Голландії Декарт написав найважливіші свої праці. Поряд з видатними математичними дослідженнями він відкрив один із законів оптики, сформулював закон збереження кількості руху, розробив нову гіпотезу про походження планет, створив фізичну теорію кровообігу, і зробив значний внесок в філософію. Вся науково-філософська діяльність Декарта була спрямована проти схоластики і церковних догм. Замість сліпої віри він висунув на перше місце силу людського мислення, розум, здатний пізнавати природу. Тому Декарт і вказував на математику як на зразок для інших наук. Саме йому належать слова: «Єдине, в чому я певен, це те, що я існую» або «Мислю, отже існую».

Математичні праці Декарта тісно пов’язані з його філософськими і фізичними дослідженнями. Філософський твір «Роздуми про метод», що вийшов в Лейдені в 1637 році складався з трьох частин: «Діоптрика», «Про метеори» і «Геометрія». В останньому викладені основи нової аналітичної геометрії. Власне, аналітична геометрія виникла, коли Декарт почав розглядати невизначені задачі на побудову, розв’язками яких є не одна, а кілька можливих довжин.

Декарт не любив довгих розрахунків. Він віддавав перевагу наочно-геометричним міркуванням і хотів працювати цим методом з будь-якими складними кривими – а не тільки із прямими й колами, як це робив Евклід. Для цієї роботи корисно вміти складати, віднімати й множити криві між собою – так само, як ми це робимо із числами. І Декарт винайшов такий спосіб,помітивши, що багато кривих на площині задаються простими рівняннями – після того як ми введемо на площині координати, зобразивши кожну точку двома числами (х, у ). 

І взагалі: кожне рівняння з двома невідомими F(x,у)=0 задає на координатній площині якусь криву! Але над рівняннями легко здійснювати будь-які арифметичні операції. Всі вони набувають геометричного сенсу, коли ми креслимо або подумки уявляємо криву, що відповідає даному рівнянню.

Таким чином ,плоскі криві можна описувати на одній із двох еквівалентних умов: наочно-геометричній, або аналітичній – через формули. Двобічний «словник», що перекладає фрази однієї з цих мов на рівнозначні фрази іншої мови, Декарт назвав аналітичною геометрією. Заклавши основи аналітичної геометрії, сам Декарт піднявся в цій області не далеко. Недосконалою була його система координат, в якій не розглядались від’ємні абсциси. Майже незадіяними залишились питання аналітичної геометрії тривимірного простору. Тим не менш «Геометрія» Декарта вплинула на розвиток математики, і на протязі 150 років алгебра і аналітична геометрія розвивались переважно в напрямах, вказаних Декартом.

В «Трактаті про конічні перерізи» (1656), який вийшов з друку в одній частині з Арифметикою нескінченних», він намагається показати переваги аналітичного методу Декарта перед синтетичним методом математиків давнини при викладі теорії конічних перерізів. Геометричні доведення він проводить з допомогою алгебри. В цьому творі Валліс вперше виразно сформулював підхід до обчислення площі криволінійної фігури, поділивши проміжок інтегрування на рівні частини. Вчений вперше ввів від’ємні абсциси і правильно застосував їх.

Погляди філософа і математика Декарта визначали його позицію щодо сновидінь. Перше питання, яке виникає для нього в цій сфері - це питання «Хто про кого бачить сон?» В основі його концепції буття лежить сумнів. Він піддавав сумніву всі судження і факти, в яких можна було знайти хоч найменше підставу для цього, включаючи істинність математичних аксіом, існування Бога і навіть себе самого. Сумніви привели Декарта лише до одного переконання, в якому він не міг засумніватися. Ця фраза відома всім: cogito ergo sum - мислю, значить існую.

    І тоді цілком закономірне його запитання: «Як ми можемо знати, що ті відчуття, які ми відчуваємо у сні, є помилковими, а ті, які ми відчуваємо наяву - щирими, якщо перші також яскраві і виразні, як і останні?» Як людина може провести чітку грань між тим, що він бачить уві сні і в реальності?

    Крім того, сумніву піддається і справжність самої інформації, що надходить до нас через органи чуття. А так як сновидіння для Декарта були нічим іншим, як результатом діяльності органів чуття сплячого, не можна вважати інформацію, отриману в них твердою основою знань.

    Крім теоретичних міркувань, необхідно відзначити біографічну сторону, пов'язану з проблемою сновидінь. Сам Декарт протягом свого життя бачив кілька важливих снів, що вплинули на його службу, які були описані в його роботах.

    Вночі 10 листопада 1619 він побачив кілька снів, які наштовхнули його на шлях пошуку істини. Декарт витлумачив ці сни, як прояв його бажання знайти метод пояснення світу, який дозволив би йому зробити це заняттям його життя. Розшифрувавши ці сни, які йому представлялися, як божественне послання, він прийшов до висновку, що його долею повинні стати пошуки істини за допомогою математичного методу, під якими він зокрема увазі аналітичну геометрію.

    У першому сновидінні він був змушений спиратися на свою ліву половину, яка була уособленням несвідомого, через те, що права половина, яка відображає його свідомість, втратила всю свою силу і не могла підтримувати його. Для Декарта, який заперечував значущість всього ірраціонального і релігійного, це був переворот, який змусив його звернути увагу на важливість нераціональної сторони буття.

Інше сновидіння зробило Декарту дві книги. Одна з них поетична антологія, яка була озаглавлена ​​«Corpus poetarum». У книзі були поміщені кілька портретів, вигравіруваних на міді, і відкривала розповідь рядок, що містить основне питання філософії: «Що є стежкою до дороги життя?» («Quod vitae sectabor iter?"). Далі йшов текст, в якому містилось інше фундаментальне питання, яке ставив перед собою Декарт: «Бути чи не бути?» («Est et non?"). Інша книга виявилася словником, в якому були представлені «всі науки, зібрані разом».

    Цей сон безпосередньо вплинув на погляди Декарта. Єдність філософії і мудрості, відбите в обох книгах, привело його до рішення, яке він не міг знайти під час неспання, і навело його на думку про єдність всіх наук.

 

Ісаак Ньютон

(1643 – 1727 рр.)

 

Ньютон був найвидатніший геній з усіх, що

будь-коли існували, і найщасливіший, бо тільки

 один раз дано людині відкрити систему світу.

                        Ж. Лагранж

 

Ісаак Ньютон – англійський фізик, механік, астроном і математик. Народився в Вулсторпі. З 12 років навчався в школі в Грантемі. З 1661 по 1665 навчався в Кембриджському університеті. З 1669 по 1701 працював в цьому університеті.

Ньютон вніс у науку стільки нового, скільки внесли Евклід і Архімед разом узяті. Або Гільберт і Архімед – теж узяті разом. Але Ньютон придумав все це один – і за лічені роки! Втім, сам Ньютон не вважав себе одинаком у науці: «Якщо я бачив далі, ніж інші, це тому, що стояв на плечах гігантів». Ньютон сам був гігантом; його постать помітно піднімається над плечима Декарта, Кеплера і Галілея. Адже Ньютон винайшов першу систему аксіом математичної фізики: це рівнозначно досягненням Евкліда в геометрії. Він створив також математичний аналіз гладких функцій: це можна порівняти з винаходом планіметрії або алгебри. Для таких успіхів треба бути не тільки генієм, але ще треба й вчасно народитися. Про себе Ньютон писав: « не знаю, чим я можу здаватися світові, але сам собі я здаюся лише хлопчиком, що бавиться на морському березі й розважається тим, що час від часу відшукує камінчик більш кольоровий, ніж звичайно, або червону черепашку, тоді як великий океан істини простягається переді мною недослідженим».

Ще в студентські роки Ньютон відкрив біноміальне розкладання для якого завгодно цілого додатного показника. Молодий учений відразу ж знайшов застосування своєму відкриттю: записав ряди для відображення сегмента й сектора кола, синуса, арксинуса, логарифмічної функції. За допомогою рядів Ньютон міг тепер вивчати властивості функцій, робити наближені обчислення. За допомогою степеневих рядів неважко обчислити похідну або інтеграл від будь-якої функції. Володіючи цими двома діями у світі функцій, можна розв’язати будь-яке диференціальне рівняння – тобто зрозуміти будь-який процес у фізичному світі. Кожен крок Ньютона на цьому шляху породжував нову теорему або виявляв новий закон природи, що відразу потрапляли в підручники. Наприклад, операції диференціювання й інтегрування функцій виявилися взаємно зворотними. Нині цей факт називають теоремою Ньютона – Лейбніца (німецький учений відкрив її незалежно від англійця), яку постійно використовують при складанні таблиць інтегралів.

Розробка диференціального й інтегрального числень стала важливим етапом у розвитку математики. Велике значення мали роботи Ньютона з алгебри, інтерполяції й геометрії. Завдяки йому алгебра остаточно звільнилася від геометричної форми; і його визначення числа не як зібрання одиниць, а як відношення довжини будь-якого відрізка до довжини відрізка, прийнятого за одиницю, стало важливим етапом у розвитку вчення про дійсне число.

Математику Ньютон вважав основним інструментом фізичних досліджень і розробляв її для численних подальших додатків. Після тривалих міркувань він дійшов до обчислення нескінченно малих на основі концепції руху; математика для нього не була абстрактним продуктом людського розуму. Він вважав, що геометричні образи – лінії, поверхні, тіла – утворюються внаслідок руху: лінія – при русі точки, поверхня – при русі лінії, тіло – при русі поверхні. Ці рухи здійснюються в часі, і за будь-який малий час точка, наприклад, пройде будь-який малий шлях. Для визначення миттєвої швидкості, в даний момент, необхідно знайти відношення приросту шляху ( за сучасною термінологією ) до приросту часу, а потім – границі цього відношення, тобто взяти «останнє відношення», коли приріст часу прямує до нуля. Так Ньютон увів відшукання «останніх відношень», похідних, які він називав флюксіями.

Використання теореми про взаємну оборотність операцій диференціювання й інтегрування і знання похідних багатьох функцій дало Ньютонові можливість одержати інтеграли. Якщо інтеграли безпосередньо не обчислювалися, Ньютон розкладав підінтегральну функцію в степеневий ряд і інтегрував його почленно. Для розкладання функцій у степеневий ряди він найчастіше користувався відкритим ним розкладанням бінома, застосовував і елементарні методи.

Новий математичний апарат був апробований ученим у головній праці його життя – «Математичних початках натуральної філософії». У той період Ньютон вже вільно володів диференціюванням, інтегруванням, розкладанням у ряд, інтегруванням диференціальних рівнянь.

 Свої відкриття Ньютон зробив раніше за Лейбніца, але вчасно не опублікував їх, бо всі його математичні твори були видані після того, як він став знаменитим. У 1666 році він підготував рукопис «Наступні пропозиції достатні, щоб розв’язувати задачі за допомогою руху», що містить основні відкриття з математики. Рукопис залишався в чорновому варіанті й був опублікований тільки через триста років.

Метод Ньютона – Лейбніца починається із заміни кривої, що обмежує площу, яку потрібно визначити послідовністю ламаних, аналогічно тому, як це робилося у винайденому греками методі вичерпування. Точна площа дорівнює границі суми площ п прямокутників, коли пнаближається до нескінченності. Ньютон показав, що цю межу можна знайти, обертаючи процес знаходження швидкості зміни функції. Операція, зворотна диференціюванню, називається інтегруванням. Твердження про те, що підсумування можна здійснити, обертаючи диференціювання, називається основною теоремою математичного аналізу.

Вклад Ньютона в математику не вичерпується створенням диференціального та інтегрального числення. В алгебрі йому належить метод чисельного розв’язування алгебраїчних рівнянь (метод Ньютона), важливі теореми про симетричні функції коренів алгебраїчних рівнянь.

Наукову діяльність Ньютона можна поділити на три періоди. В 1665–1667 роках він натхненно працював, відкриваючи основні закони природи і математики. Вже в 27 років професор Ньютон став визнаним «королем математиків і фізиків». Наступні 20 років він присвятив строгому доведенню відкритих ним законів, розрахунку найважливіших задач (включаючи рух Місяця й планет) і написанню своєї головної книги: «Математичні принципи філософії природи». В останні 40 років життя Ньютон мало займався наукою: він лише публікував раніше підготовлені ним книги, часом відволікаючись на розв’язування особливо важкої й цікавої задачі за допомогою математичного аналізу.

 

Блез Паскаль

(1623 – 1662 рр.)

 

…розум сугубо математичний правильно

працюватиме, тільки коли йому заздалегідь відомі

всі означення й начала, у противному разі він збивається

з пантелику і стає нестерпним, бо правильно працює лише

на основі чітко сформульованих начал.

                                   Б. Паскаль

 

 

 

 

 

 

 

 

 

 

 

 

Блез Паскаль – французький математик, фізик і філософ. Народився в сім’ї Е. Паскаля (французького математика – любителя ) в Клермон-Ферране. В 1631 році він разом з сім’єю переїжджає в Париж. Паскаль, який рано виявив видатні математичні здібності, являє класичний приклад геніальності отроків. Зовсім малий, він розмірковував про «високі матерії», справляв на оточуючих враження крихітної дорослої людини, а ще він вражав своїми короткими, досить точними відповідями, а ще більше – питаннями про природу речей. А вже в 18-літньому віці Блез винайшов лічильну машину – «бабусю» майбутніх арифмометрів. Юний конструктор записав, не знаючи ще, що думка його на століття випереджає свій час: «Обчислювальна машина виконує дії, що наближаються до думки більше, ніж усе те, що роблять тварини». Машина принесла йому популярність. Його формули і теореми могли оцінювати лише лічені люди, а тут машина – подумати тільки – рахує сама! Юрби людей квапились в Люксембурзький сад, щоб подивитися на диво-машину, про неї складали вірші, їй приписували фантастичні можливості. Так Блез Паскаль став знаменитою людиною.

В Е. Паскаля і в деяких його приятелів – М. Мерсенна, Ж. Роберваля та ін. – кожен тиждень збирались математики і фізики. Ці зібрання з часом набули форми наукових зібрань. На базі цього гуртка була створена Паризька АН (1666). З 16 років в роботі гуртка приймав участь і Паскаль. В цей час він написав свою першу роботу про конічні перерізи, в якій висказав одну з важливих теорем проективної геометрії: точки перетину протилежних сторін шестикутника, вписаного в конічний переріз, лежать на одній прямій. Паскаль присвятив ряд праць арифметичним рядам і біноміальним коефіцієнтам. В «Трактаті про арифметичний трикутник» він ввів так званий трикутник Паскаля.  Біноміальні коефіцієнти Паскаль утворював по розробленому ним методу повної математичної індукції – в цьому полягало одне з важливіших його відкриттів. Новим було те, що біноміальні коефіцієнти виступали тут як числа комбінацій зп елементів по т і потім використовувались в задачах теорії ймовірностей. До того часу ніхто з математиків ймовірність подій не обчислював. Паскаль і Ферма знайшли ключ до розв’язування таких задач. В листуванні цих вчених теорія ймовірностей і комбінаторика були по справжньому науково обґрунтовані. Є всі підстави стверджувати, що Паскаль і Ферма – засновники нової області математики – теорії ймовірностей.

Важливим є також «Трактат про синуси чверті круга». Обчислюючи інтеграли тригонометричних функцій, особливо тангенса, Паскаль ввів тут еліптичні інтеграли, які пізніше зіграли важливу роль в аналізі і його застосуваннях. Крім цього, вчений довів ряд теорем, що стосуються заміни змінних і інтегрування частинами.

В галузі філософії Паскаль чітко сформулював основні тези наукового пізнання, розвинув поняття «філософія розуму» і «філософія серця». На його честь названа одиниця тиску – паскаль.

 

 

 

Вільгельм Лейбніц

(1646 – 1716 рр.)

 

Навряд чи можна вважати випадком ту обставину,

що така людина, як Лейбніц, який був такою самою мірою

абстрактним мислителем першого рангу, як і людиною

видатних практичних обдарувань, є одночасно як батьком

суто формальної математики, так і винахідником першої

обчислювальної машини. 

                                     Ф. Клейн 

 

 

 

 

 

 

 

 

 

 

 

 

Вільгельм Лейбніц – німецький математик, фізик і філософ. Народився в Лейпцигу. Він, як і Ньютон, був вундеркіндом: ще у вісім років він самостійно вивчив латину, а ще через два роки – давньогрецьку мову. А нині багато хто називає Лейбніца останнім ученим епохи Відродження, або першим ученим епохи Просвітництва. Те і те вірно. Перше – тому, що до наших днів ще в жодної людини не було поєднання такого яскравого математичного таланту з широтою гуманітарних схильностей. Щодо цього Лейбніца можна зрівняти з Арістотилем, Леонардо да Вінчі, або Рене Декартом. Інше звання Лейбніца також виправдане, адже він став першим академіком двох найвизначніших наукових співдружностей Європи: Лондонського Королівського Товариства й Паризької Академії наук. А пізніше Лейбніц виявився засновником ще двох академій. В 1700 році він став президентом і організатором Прусської Академії наук у Берліні. До Петербурга він не дістався, але, на прохання Петра І, встиг скласти проект Російської Академії наук, що була заснована в 1725 році – вже після смерті її ініціаторів.

В 1661 році Лейбніц вступив на юридичний факультет Лейпцігського університету. Крім юридичних наук вивчав філософію і математику. В університеті ознайомився з працями Арістотеля і Декарта. Захистив дисертацію на ступінь бакалавра (1663), магістра філософії (1664) і доктора права (1666). Перебував на юридичній службі при дворі Майнцського курфюрста. З Майнця він виїжджав з дипломатичною місією в Париж. Діяльність Лейбніца виходила далеко за межі офіційних обов’язків. Він займається і питаннями хімії, геології. Особливо плідною була наукова діяльність Лейбніца в області математики. В 1666 році він опублікував свою першу математичну працю «Роздуми про комбінаторне мистецтво». Сконструйована ним обчислювальна машина виконувала не лише додавання і віднімання, як це було у Паскаля, але й множення, ділення, піднесення до степеня і добування квадратного і кубічного коренів. Понад 40 років Лейбніц присвятив вдосконаленню свого винаходу. Саме тому його можна вважати ідейним надихачем сучасної машинної математики.

В 1676 році Лейбніц заклав перші підвалини великого математичного методу, відомого за назвою «диференціальне числення». Факти досить переконливо доводять, що вчений хоча й не знав про ньютонівський метод флексій, але був підведений до його відкриття листами великого вченого. У листі, написаному в червні 1677 року, Лейбніц прямо розкривав Ньютонові свій метод диференціального числення, але той не відповів. Ньютон вважав, що відкриття належить йому навічно, і при цьому досить того, що воно було заховане лише в його голові. Учений щиро вважав: своєчасна публікація не дає ніяких прав. Перед Богом першовідкривачем завжди залишиться той, хто відкрив першим. З іншого боку, нема ніякого сумніву, що відкриття Лейбніца за рівнем сприйняття, за зручністю позначень й докладною розробкою методу стало знаряддям аналізу значно могутнішим й популярнішим за ньютонівське. Навіть співвітчизники Ньютона, що довгий час надавали перевагу методу флексій, помалу засвоїли більш зручні позначення Лейбніца.

Хоча політична діяльність Лейбніца (він був дипломатом) значною мірою відволікала його від занять математикою, весь свій вільний час він присвячував обробці винайденого ним диференціального числення й у проміжок часу між 1677 і 1684 роками встиг створити нову галузь математики. У 1684 році вчений надрукував у журналі «Праці вчених» систематичний виклад початків диференціального числення. Усі опубліковані ним трактати, надали науці такого великого поштовху, що за тих часів важко навіть було оцінити все значення реформи, яку здійснив Лейбніц у галузі математики. Те, про що кращі французькі й англійські математики, окрім Ньютона, мали лише невиразне уявлення, стало раптом ясним, виразним, загальнодоступним, чого не можна сказати про геніальний метод Ньютона. Слід відмітити, що саме Лейбніц склав першу таблицю похідних та інтегралів від елементарних функцій.  

Лейбніц був дуже різнобічним вченим. Крім «безперервної» математики функцій і похідних, він дуже цікавився «дискретною» математикою. Почавши з винаходу вдалого арифмометра, вчений невдовзі помітив особливу зручність двійкової системи числення для математичних машин. Він також розвив математичну логіку, перейшовши від словесних міркувань Арістотеля до алгебричного обчислювання логічних висловлювань. Про це ще мріяв в XIV ст. Раймонд Луллій. Розвиваючи його ідеї, Лейбніц замислився над повною формалізацією людського мислення, над створенням «розумних машин». У своїх сподіваннях Лейбніц помилився – але щоб виявити його помилку, математикам XX ст. довелося побудувати електронні комп’ютери та зрівняти їхню роботу з діяльністю людського мозку.

У віці 12 років Лейбніц уже був знавцем латині; у віці 13 років він за один ранок склав триста гекзаметрів латинського вірша для спеціального заходу в школі. У віці 14 років, Лейбніц вступив до Лейпцизького університету, через 2 роки  отримав ступінь бакалавра, з дисертацією «De Principio Individui», з якої бере початок його пізніша теорія монад.
Лейбніц навчався у Йенському університеті, де на нього вчинив великий вплив філософ і математик Ерхард Вейгель.
Лейбніц був трохи скупий. Коли яка-небудь молода фрейліна Ганноверського двору виходила заміж, він зазвичай підносив їй те, що називав «весільним подарунком», яке складалося з корисних правил, закінчувалися радою не відмовлятися від умовно тепер, коли вона дістала чоловіка.
З 1667 до 1676 р. перебував на службі Майнського курфюрста, барона Йоганна Кристіана фон Бойнебурґа.
Загальновідома філософія Лейбніца викладена в «Монадологія» і в «Началах природи і благодаті»; одну з названих робіт (невідомо яку) він написав для принца Євгенія Савойського, товариша по службі герцога Мальборо. Основа його теологічного оптимізму викладається в «теодицеї», яку він написав для королеви Шарлотти Прусської.
Лейбніц надавав надзвичайну увагу питанням зручної наукової нотації, і в рукописі від 21 листопада 1675 р. він уперше використав нині загальновизнанний запис  для інтегралу функції.
Великий французький філософ-енциклопедист Дідро писаву своїй знаменитій "Енциклопедії", що для НімеччиниЛейбніц став тим, чим для Стародавньої Греції були Платон, Арістотель і Архімед, разом узяті.

 

 

              Леонард   Ейлер

(1707 – 1783 рр.)

 

Ейлер був насамперед математиком, що

сприймав і розвивав математику як єдине ціле,

але він знав, що ґрунтом, на якому розквітає

математика, є практична діяльність. 

                      М. О. Лаврентьєв

 

 

 

 

 

 

 

 

 

 

Леонард Ейлер – видатний математик, механік, фізик і астроном. Народився в Базелі в сім’ї пастора Пауля Ейлера, який захоплювався математикою. Ейлер закінчив Базельську гімназію, навчався в Базельському університеті на філософському, а потім на богословському факультеті. Одночасно відвідував лекції Йоганна Бернуллі, що й визначило його подальшу долю. Творча діяльність Ейлера тісно пов’язана з Петербурзькою академією наук, де він приймав саму активну участь в різних напрямках наукової роботи. За 15 років свого першого перебування в Росії Ейлер встиг написати перший у світі підручник з теоретичної механіки, а також курс математичної навігації й багато інших праць. Писав Ейлер легко і швидко, простою і зрозумілою мовою. Ейлер був всебічно обдарованим вченим: знав грецьку, латинську, німецьку, французьку, російську та інші мови; крім математики , фізики, астрономії, мав глибокі знання з географії, хімії, анатомії, медицини, тощо. Він дуже любив музику, класиків давньої літератури, зокрема, знав напам’ять «Енеїду» Вергілія. Ейлер був веселою, скромною і співчутливою людиною. Він відрізнявся рідкісною працездатністю і був не лише геніальним математиком, але й чудовим фізиком, інженером, астрономом, географом.

В 1741 – 1766 роках Ейлер працював в Берлінській академії наук, якою, починаючи з 1759 року, фактично керував. Час, проведений у Берліні, учений вважав кращим у своєму житті.

Значний внесок Ейлер зробив і в геометрію. Він шукав у ній не стільки нові витончені факти, скільки загальні теореми, що не укладаються в догматику Евкліда. Наприклад, теорема про зв'язок між кількістю вершин, ребер і граней опуклого багатогранника:

               В – Р + Г = 2.   

Цю формулу знав ще Декарт; але він не залишив її доведення. Ейлер легко знайшов доведення цієї теореми, а потім замислився: якщо формула справедлива для всіх опуклих тіл, то яку ж властивість вона виражає? Можливо, властивість сфери, у яку можна деформувати будь-який опуклий багатогранник? Якщо так, то ця формула навряд чи справедлива для інших замкнутих поверхонь – на зразок тора чи кренделя! Перевірка показала: для деяких карт на торі вираз В – Р + Г  набуває значення 0, а на кренделі – значення (-2). Але довести ці тотожності для карт на складних поверхнях Ейлер не зумів і залишив цю проблему нащадкам.

Але більша частина робіт Ейлера присвячена аналізу. Ще в 1743 році він видав п’ять мемуарів, із них чотири з математики. В одній з цих праць вказується на спосіб інтегрування раціональних дробів шляхом розкладання їх на частки дробу й, крім того, викладається звичайний тепер спосіб інтегрування лінійних звичайних рівнянь вищого порядку з сталими коефіцієнтами. Та найвищим досягненням Ейлера в математиці є доведення основної теореми алгебри, яке було опубліковане в 1751 році в роботі «Дослідження про уявні корені рівнянь».

Основна теорема полягала в тому, що всі корені рівняння належать полю комплексних чисел. Для доведення цього Ейлер установив, що всякий багаточлен з дійсними коефіцієнтами можна розкласти в добуток дійсних лінійних або квадратичних множників.

Значення чисел, що не є дійсними, Ейлер називав уявними і вказував на те, що звичайно вважають їх такими, які попарно в сумі й добутку дають дійсні числа. Отже, якщо уявний корінь дорівнюватиме 2t,то це дасть t дійсних квадратичних множників у поданні багаточлена. Ейлер пише: «Тому говорять, що кожне рівняння, яке не можна розкласти на дійсні прості множники, має завжди дійсні множники другого степеня. Однак ніхто, наскільки я знаю, ще не довів досить чітко істинність цієї думки; отже, я постараюся довести це таким чином, щоб охопити всі без винятку випадки».

Після повернення в Росію, в 70-ті роки XVII століття навколо Ейлера виросла Петербурзька математична школа, яка більш ніж наполовину складалася з російських вчених. Тоді ж завершилась публікація головної книги його життя – «Основи диференціального й інтегрального числень», за якою вчилися всі європейські математики з 1755 по 1830 рік. «Основи» вигідно відрізняються від «Початків» Евкліда й від «Принципів» Ньютона. Звівши струнку будову математичного аналізу від самого фундаменту, Ейлер не прибрав ті риштовання та сходинки, якими він сам підіймався до своїх відкриттів. Багато цікавих здогадок і початкові ідеї доведень збережені в тексті – незважаючи на помилки, які в них трапляються, – аби вони були наукою для всіх спадкоємців Ейлеревої думки. Це був перший підручник, призначений не для послідовників, а для дослідників: таким був заповіт Ейлера й усієї епохи Просвітительства адресований прийдешнім століттям і народам.

 

Карл Фрідріх Гаусс

(1777 – 1855 рр.)

 

Серед геніальних представників нашої науки лише

два великих попередники Гаусса – Архімед і Ньютон – були

так само щедро обдаровані природою, як він.

                                                  Ф. Клейн

 

 

 

 

 

 

 

 

 

 

 

Гаусс – великий німецький математик. Народився в місті Брауншвейзі в сім’ї водопровідника. З раннього дитинства проявив видатні математичні здібності, – і звичайно, першим його захопленням стала арифметика. В дев’ять років він під час шкільного уроку … відкрив формулу суми арифметичної прогресії. Пізніше Гаусс переніс всі теореми арифметики натуральних чисел на багаточлени й на цілі комплексні числа. У підсумку в алгебрі з’явилося загальне поняття кільця. Одночасно з’ясувалося, що множина простих чисел виду (4к + 1) нескінченна і що всі їх можна уявити у вигляді суми двох квадратів. Це був перший новий факт такого роду, відкритий із часів Ератосфена. Пізніше учень Гаусса – Пітер Діріхле – набагато перевершив учителя, довівши, що в будь-якій арифметичній прогресії міститься нескінченна множина простих чисел.

Гаусс до старості зберіг юнацьку жадобу до знань і величезну допитливість. Наприклад, у 62 роки він швидко вивчив російську мову, щоб самому розібратися в працях свого колеги – Миколи Лобачевського. Але звичайно Гаусс уникав читати чужі статті або книги. Йому вистачало формулювання основного результату; доведення він придумував сам, заодно відкриваючи багато фактів, на які не звернув уваги сам автор. Така звичка сформувалась замолоду, коли 19-літній Гаусс вирішив сам освоїти всі досягнення й методи алгебри, не пропускаючи жодного яскравого додатка до цієї древньої науки.

Результат був вражаючий. Гаусс знайшов алгебричне доведення нерозв’язності багатьох задач на побудову циркулем і лінійкою, які непокоїли ще Піфагора. Ключова ідея Гаусса дуже проста: треба зобразити точки площини комплексними числами, і тоді геометрична задача перетвориться на алгебраїчну! Але як довести нерозв’язність алгебраїчної задачі? Гаусс помітив, що будь-яка побудова циркулем і лінійкою зводиться до розв’язування ланцюжка квадратних рівнянь. А кожна «непокірлива» задача на побудову зводиться до розв’язування рівняння-багаточлена степеня більше, ніж 2.Чому ж розв’язування такого рівняння іноді не зводиться до розв’язування квадратних рівнянь? Отут мало одних розрахунків; потрібно вводити нові математичні поняття, що відбивають суть справи.

Гаусс винайшов два таких поняття: поле і векторний простір. У підсумку векторна алгебра, давно звична фізикам і геометрам, стала самостійною алгебраїчною наукою. Виявилося, що комплексне число, досяжне за допомогою циркуля і лінійки, лежить у деякому полі розмірності 2к, а всякий корінь нерозкладного багаточлена степеня к лежить у полі розмірностік. Якщо число, що цікавить нас, лежить у тім і в іншому – виходить, число 2к ділиться на к; тобто саме число к є степенем двійки. Із цього міркування випливає, що корінь будь-якого нерозкладного багаточлена третього степеня не можна побудувати циркулем і лінійкою. Наприклад, не вдається розділити на три рівні частини кут в , або побудувати трикутник по трьох нерівних медіанах. Така ж заборона перешкоджає діленню кола на 7, 9, 11, 13 або 25 рівних частин. Але для ділення на 5 або на 17 частин заборони немає, оскільки числа 5 – 1 = 4 і 17 – 1 = 16 суть степені двійки. Тому елліни знайшли спосіб побудови правильного п’ятикутника, а Гауссу вдалося побудувати правильний 17-кутник.

До 24 років Гаусс увійшов до числа найвідоміших математиків Європи. У 30 років Гаусса вважали вже «королем» європейських математиків. Чудовий успіх в області геометричних побудов спонукав Гаусса до пошуків нових доведень. Він захопився загадкою п’ятого Евклідового постулату про паралельні прямі. В 1818 році Гаусс здогадався, що цей постулат може мати інше формулювання – але не на площині, а на інших поверхнях, не відомих Евкліду. До кінця життя Гаусс мовчав про свої відкриття в галузі геометрії – навіть після того, як їх повторили більш молоді математики: М. Лобачевський і Я. Больяї. В чому ж річ? Чому Гаусс не повідомив про свою гіпотезу про паралельні прямі хоча б у вузькому колі математиків? Адже саме так зробив Піфагор, виявивши несумірність діагоналі квадрата з його стороною! Імовірно, Гаусс міркував так: якщо постулат про паралельні прямі є незалежним від інших аксіом, то зникає єдина наука геометрія! Вона розділяється принаймні на три галузі – відповідно до трьох варіантів постулату про паралельні ( за Евклідом, за Ріманном й за Лобачевським). А що далі? Чи не продовжиться процес розгалуження геометричної науки необмежено – після кожної нової аксіоми? Чи не пошириться цей процес на всю математику? І хто захоче працювати в такій роздробленій науці?

Мабуть, так міркував вчений , – і мовчав, не в змозі відповісти ні собі, ні іншим на це питання. Але вченому треба жити і працювати – навіть коли його розум не дає відповіді на ті питання, що його непокоять. Після 1820 року Гаусс захопився геометрією довільних гладких поверхонь. Він дав визначення їхньої кривизни і знайшов несподіваний зв'язок кривизни з Ейлеревою характеристикою поверхні. У 1798 році Гаусс підготував дисертацію, присвячену доведенню основної теореми алгебри, а вже 1801 року побачили світ знамениті «Арифметичні дослідження» Гаусса. Ця книга (понад 500 сторінок великого формату) містить основні результати його міркувань. Закони взаємності дотепер посідають одне із центральних місць в алгебраїчній теорії чисел.

Вчений залишив після себе відразу чотири доведення основної теореми алгебри. Першому доведенню він присвятив випущеному в 1799 році докторську дисертацію на цю тему. Повз увагу Гаусса не пройшли «білі плями» в роботі Ейлера. Перше доведення Гаусса було аналітичним. У другому доведенні математик знову повернувся до критики доведення основної теореми алгебри за допомогою міркування, коли заздалегідь передбачається існування коренів рівняння.

Гаусс так пояснив у вступному параграфі необхідність нового доведення: «Хоча доведення про розкладання цілої раціональної функції на множники, що я дав у мемуарах, опублікованих 16 років тому, не залишає бажати кращого стосовно строгості й простоти, треба сподіватися, що математики не вважатимуть за небажане, що я знову повертаюся до цього надзвичайно важливого питання і будую друге, не менш строге доведення, виходячи із зовсім інших принципів. А саме, це перше доведення залежало частково від геометричних розглядів, тоді як те, що я тут починаю пояснювати, ґрунтується на суто аналітичних принципах». Слід зазначити, що аналітичним Гаусс називає той метод, який сьогодні називається алгебраїчним.

Для доведення Гаусс використовував побудови поля розкладання багаточлена. Минуло понад шістдесят років, коли й Л. Кронекер удосконалив і розвинув метод Гаусса для побудови поля розкладання будь-якого багаточлена. Згодом Гаусс дав ще два доведення основної теореми алгебри. Четверте і останнє датоване 1848 роком.

Не забував Гаусс і про комплексні числа, які так допомогли йому розібратися в таємницях геометричних побудов. Ніби розважаючись, вчений придумував все нові доведення своєї теореми про те, що всякий багаточлен має комплексний корінь. Мабуть, Гаусс хотів зрозуміти: чи має ця «суто алгебрична» проблема хоч один суто алгебраїчний розв’язок, або є неминучими комбінації алгебри з геометрією, або з математичним аналізом?

Виявилося, що такі комбінації неминучі. Будь-яка складна проблема розв’язується лише після кількох її перекладів з однієї математичної мови на іншу. І ось уже два століття вся математична наука розвивається в системі взаємодопомоги й сплітання її різних галузей. Гаусс першим почав працювати в такій системі: немов би перекидаючи палаюче вугілля з однієї долоні на іншу. За це його шанобливо називають «батьком сучасної математики»

 

Герон Александрійський

    Герон жив в Єгипті в місті Александрія і тому став відомий як Герон Александрійський. Сучасні історики припускають, що він жив в 1-м столітті н.е. десь між 10-75 роками. Встановлено, що Герон викладав в Александрійському Музеї - науковому центрі античного Єгипту, до складу якого входила і знаменита Александрійська бібліотека. Більшість праць Герона представлена у вигляді коментарів і записок до учбових курсів з різних навчальних дисциплін. Нажаль, оригінали цих праць не збереглися, можливо, вони загинули в полум'ї пожежі, що охопило Александрійську бібліотеку в 273 році н.е., а можливо були знищені в 391 році н.е. християнами в пориві релігійного фанатизму, коли вони знищували все, що нагадувало про язичницьку культуру. До наших часів дійшли лише переписані копії праць Герона виконані його учнями і послідовниками. Частина з них на грецькій мові, а частина на арабській. Є переклади на латину, виконані в XVI столітті. 
    Найбільш відома "Метрика" Герона - наукова праця, в якій наведені визначення кульового сегменту, тора, правила і формули для точного і наближеного обчислення площ правильних багатокутників, об'ємів зрізаних конуса і піраміди. В "Метриці" є знаменита формула Герона для визначення площі трикутника за трьома сторонами, наведені правила чисельного розв’язання квадратних рівнянь і наближеного вилучення квадратних і кубічних коренів. В "Метриці" досліджуються найпростіші підйомні пристосування - важіль, блок, клин, похила площина і гвинт, а також деякі їх комбінації. В цій праці Герон вводить в обіг термін "прості машини" і використовує для опису їх роботи поняття моменту сили. 
    Багато математиків звинувачують Герона в тому, що в "Метриці" нема математичних доказів. Це справді так. Герон не був теоретиком, він вважав, що всі виведені ним формули і правила ліпше пояснювати наочними практичними прикладами. Саме в області практики Герон перевершує більшість своїх попередників. Кращою ілюстрацією цього є його праця "Про діоптр", знайдена лише в 1814 році. В цій праці описані методи проведення різноманітних геодезичних робіт, причому землемірна зйомка виконується за допомогою винайденого Героном приладу - діоптри.

Мал. 2. Діоптра

   Діоптра була прототипом сучасного теодоліта. Головною її частиною була лінійка з закріпленими на її кінцях візирами. Ця лінійка оберталася по колу, що могло бути розташовано горизонтально чи вертикально. Для правильного встановлення приладу використовували висок і рівень. За допомогою приладу і прямокутних координат, Герон міг вирішувати на місцевості різні задачі: вимірювати відстань між двома точками, коли одна з них або обидві вони недоступні спостерігачеві; провести пряму, перпендикулярну до недоступної прямої лінії; знайти різницю рівнів між двома пунктами; виміряти площу найпростішої фігури.
    Ще за часів Герона одним з шедеврів античної інженерії вважався водопровід на острові Самос, що був створений за проектом Евпаліна і проходив крізь тунель. Вода через цей тунель подавалася в місто з джерела, що знаходилося на іншому боці сторони гори Кастро. Відомо було, що з метою прискорення роботи, тунель будували одночасно з обох сторін гори, а це вимагало високої кваліфікації від інженера, що керував будівництвом. Водопровід працював багато століть і дивував сучасників Герона, також про нього згадував в своїх творах і Геродот. Саме від Геродота сучасний мир дізнався про існування тунелю Евпаліна. Дізнався, але не повірив, тому що вважалося, що стародавні греки не мали необхідної технології для спорудження такого складного об'єкту. Вивчивши знайдену в 1814 році працю Герона "Про діоптр" учені одержали друге документальне підтвердження існування тунелю. І лише в кінці XIX століття німецька археологічна експедиція насправді знайшла легендарний тунель Евпаліна.
    От як в своїй праці Герон наводить приклад використовування винайденої їм діоптри для спорудження тунелю Евпаліна.

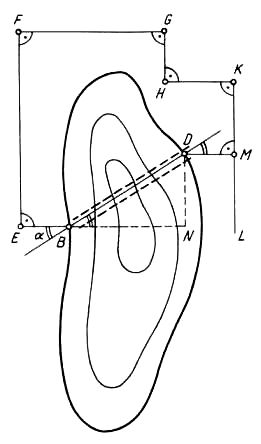
Мал. 3. Схема вимірювань для спорудження тунелю Евпаліна

   Точки B і D - входи в тунель. Поряд з точкою B обирається точка E, від неї вздовж гори будується відрізок EF, перпендикулярний відрізку BE. Далі в обхід гори будується система взаємно перпендикулярних відрізків до тих пір, поки не отримають лінію КL, на якій обирають точку M і будують від неї перпендикуляр MD до входу в тунель D. Використовуючи лінії DN і NB отримують трикутник BND і вимірюють кут α.

   Крім всього іншого в 34-му розділі праці "Про діоптр" Герон наводить опис винайденого ним пристрою для вимірювання відстаней - одометра.

 

Мал. 4. Одометр (зовнішній вигляд)

 

Мал. 5. Одометр (внутрішній устрій)

    Одометр був невеличким візком, встановленим на двох колесах спеціально підібраного діаметра. Колеса поверталися рівно 400 разів на мілліатрій (стародавня міра довжини, що дорівнює 1598 м). За допомогою зубчастої передачі в обертання приводилися численні колеса і осі, а індикатором пройденої відстані були камінчики, що випадали в спеціальний лоток. Для того, щоб дізнатися, яка відстань була пройдена, потрібно було лише підрахувати кількість камінчиків в лотку.
    Ще одним цікавим винаходом Герона, пов’язаним із застосуванням пари, є паровий бойлер.

Мал. 7. Паровий бойлер

   Бойлер містив велику бронзову ємність, з коаксіально встановленим циліндром, жаровнею і трубами для подачі холодної і виведення гарячої води. Бойлер був достатньо економічним і забезпечував швидкий нагрів води.
   Значну частину "Пневматики" Герона займає опис різних сифонів і судин, з яких самопливом по трубці витікає вода. Принцип закладений в цих конструкціях з успіхом використовується сучасними водіями при необхідності відлити бензин з бака автомобіля.
      А ось ще одна винайдена Героном конструкція судини для перетворенню води у вино і навпаки.

Мал. 8. Амфора для розливу вина і води

    Половина амфори наповнюється вином, а друга половина водою. Потім шийка амфори закривається пробкою. Розлив рідини відбувається за допомогою крана, розташованого внизу амфори. У верхній частині судини під виступаючими ручками просвердлені два отвори: один у "винній" частині, а другий в "водяній" частині. Кубок підносився до крана, жрець відкривав його і наливав в кубок або вино, або воду, непомітно затикаючи один з отворів пальцем.
   Унікальним для свого часу винаходом був водяний насос, конструкція якого описана Героном в його книзі "Пневматика".

Мал. 9. Насос Герона

   Насос складався з двох сполучених поршневих циліндрів, обладнаних клапанами, з яких по черзі витіснялася вода. Насос приводився в дію мускульною силою двох людей, які по черзі натискували на плечі важеля. Відомо, що насоси такого типу згодом використовувалися римлянами для гасіння пожеж і відрізнялися високою якістю виготовлення і напрочуд точною підгонкою всіх деталей. Подібні їм насоси аж до відкриття електрики часто використовувалися як і для гасіння пожеж, так і у флоті для відкачування води з трюмів при аварії.
    Як ми бачимо, Героном було розроблене три дуже цікавих винаходи: еоліпіл, поршневий насос і бойлер. Скомпонувавши їх можна було одержати парову машину. Така задача, напевно, була під силу якщо не самому Герону, то його послідовникам.    Тим кому повезло з шкільним вчителем фізики, напевно знають про фонтан Герона.

Мал. 10. Фонтан Герона

    Фонтан Герона складається з трьох сполучених ємностей, розміщених один над одним. Дві нижні ємності - закриті, а верхня виконана у формі відкритої чаші, в яку наливається вода. Також вода наливається і в середню ємність, яку потім закривають. По трубці, що йде від дна чаші майже до дна нижньої ємності, вода тече з чаші вниз і, стискаючи повітря, що знаходиться там, збільшує його пружність. Нижня судина сполучена з середньою за допомогою трубки, якою тиск повітря передається в середню ємність. Тиснучи на воду, повітря примушує її підійматися з середньої ємності по трубці у верхню чашу, де з кінця цієї трубки, що розташована над поверхнею води, б'є фонтан. Вода фонтану, падає в чашу, тече з неї по трубці в нижню ємність, де рівень води поступово підвищується, а рівень води в середній ємності знижується. Незабаром фонтан перестає працювати. Щоб запустити його знову, треба просто поміняти місцями нижню і середню ємності..
    В "Пневматиці" Герона також наведений опис конструкції шприца.

Мал. 11. Шприц

   Нажаль, точно невідомо чи використовувався в епоху античності цей прилад для медичних цілей. Також невідомо, чи знали про його існування француз Чарльз Праваз і шотландець Олександр Вуд, які вважаються винахідниками сучасного медичного шприца. 
    Вперше в історії Героном були розроблений самохідний механізм.

Мал. 12. Самохідна шафа

   Механізм мав вигляд дерев'яної шафи встановленої на чотирьох колесах. Внутрішній устрій шафи був схований за дверцями. Проте, секрет пересування був простий: усередині шафи поволі опускалася підвішена плита, яка за допомогою канатів і валів приводила в рух всю конструкцію. Як регулятор швидкості використовувався запас піску, який поступово пересипався з верхньої частини шафи в нижню. Швидкість опускання плити регулювалася швидкістю пересипання піску, яка залежала від того наскільки широко розкриті стулки, що відділяли верхню частину шафи від нижньої.

   Протягом свого життя Герон створив багато різноманітних винаходів, цікавих не тільки його сучасникам, але і нам.  

Ім'ям Герона названа і формула площі трикутника 

•                               Ще одна формула площі трикутника, для доведення якої можна використати тригонометричні функції, була наведена давньогрецьким математиком Героном Александрійським (прибл. І ст. до н. е.) і отримала його ім’я. Тільки у ХХ ст. з’ясувалося, що раніше за Герона цю формулу винайшов Архімед
•                               Якщо a, b, c – сторони трикутника, a+ b+ c p= 2 - півпериметр трикутника, то площа трикутника S = √p( p − a)( p − b)( p − c

 Якщо a, b, c – сторони трикутника, a+ b+ c p= 2 -

 

Микола Іванович Лобачевський

(1792 – 1856 рр.)

 

Як учений Лобачевський є в повному розумінні слова

революціонером у науці: до його відкриття нікому не приходило

в голову сумніватися в тому, що евклідова геометрія становить

єдину можливу систему геометрично пізнання, єдину можливу

сукупність тверджень про просторові форми.

                                        П.С. Александров  

 

 

 

 

 

 

 

 

 

 

Микола Іванович Лобачевський – видатний російський математик, творець неевклідової геометрії. Народився в місті Нижній Новгород в сім’ї дрібного чиновника. Після смерті батька Микола був зарахований, дякуючи старанням матері, в Казанську гімназію. Після закінчення гімназії, в 1807 році Лобачевський став студентом Казанського університету. З цього моменту все життя вченого було тісно пов’язане з Казанню і її університетом.

Молодий студент Лобачевський працював з великим ентузіазмом і вже за перші два-три роки оволодів матеріалом з області точних наук. Він був одним із най здібніших студентів університету. В 1811році закінчив університет і був залишений для подальшої наукової роботи. Лобачевський швидко просунувся на науково-педагогічному рівні завдячуючи не лише великим здібностям, але й впертій праці. Він глибоко вивчав старі й нові класичні твори видатних математиків. І вже з 1816 році , в якості професора, Лобачевський викладав в університеті спеціальні курси елементарної математики, диференціального і інтегрального числення, а пізніше йому було доручено і викладання фізики, механіки і астрономії. На протязі більше 40 років М.І. Лобачевський приймав саму активну участь в житті, організації і будівництві Казанського університету. Двічі до 1825 року він обирався деканом фізико-математичного факультету, а з 1827 року на протязі 19 років був ректором Казанського університету. Лобачевський віддавав багато сил і часу завданням виховання молоді і вніс цінний вклад у справу розвитку російської педагогічної думки.

Паралельно з просвітницькою, суспільною, педагогічною і адміністративною діяльністю розвивалась і наукова творчість Лобачевського. Багато нового вніс він в різні області математики, фізики і астрономії. Але світова слава прийде до нього із створенням нової геометричної системи.

В перші роки професорської діяльності Лобачевський, подібно іншим математикам, спочатку теж намагався довести 5-й постулат Евкліда. Застосовуючи метод доведення від супротивного, він відкидає 5-й постулат і замість нього приєднує до решти аксіом евклідової геометрії нову аксіому про паралельні прямі, прямо протилежну евклідовій аксіомі, що має назву «аксіома Лобачевського»: в площині через точку поза прямою можна провести по крайній мірі дві прямі, що не перетинають дану пряму.

Якщо б п’ятий постулат був наслідком інших евклідових аксіом, то аксіома Лобачевського повинна була б привести до протиріччя. Виводячи все нові і нові наслідки із зробленого ним припущення, Лобачевський констатував, що ні до якого логічного протиріччя воно не приводить, а навпаки, отримані результати і наслідки утворюють нову логічно струнку геометрію. Це впевнило його в тому, що п’ятий постулат не залежить від інших аксіом евклідової геометрії, з них не випливає і тому його довести неможливо.

Так була вирішена проблема п’ятого постулату.

Нова, побудована Лобачевським геометрія була названа «уявною ». Гаусс її назвав «неевклідовою», ми ж в даний час називаємо її «геометрією Лобачевського»

Ідеї Лобачевського були настільки оригінальними і неочікуваними а до того ще й випередили своє століття, що їх не зрозуміли навіть великі математики того часу. Геометрія Лобачевського не була признана сучасниками, її зустріли з байдужістю чи навіть з іронією. Презирливе ставлення до нової геометрії не змінилось на протязі всього життя її творця. Але навіть залишившись на самоті, вчений не відмовився від своїх ідей. Він не лише був впевнений в логічній несуперечності нової геометрії, але твердо вірив і в її застосування в реальному фізичному просторі. Він стверджував, що лише дослідним шляхом можна перевірити, відповідає та чи інша геометрична система законам фізики і астрономії. З цією ж метою він проводив астрономічні спостереження і вимірювання, щоб встановити, чому ж дорівнює сума внутрішніх кутів трикутника. Але такі вимірювання не могли і не можуть дати визначеного результату в силу недостатньої точності інструментів і наближеного характеру будь-яких вимірювань. Хоча розвиток науки і техніки в той час не дозволяв підтвердити теорію вченого, він не переставав вірити, що перемога його ідей настане, і навіть незадовго до смерті, вже сліпий, він диктує свою «Пангеометрію».

Лобачевському належать також фундаментальні праці з алгебри і математичного аналізу. Він першим встановив різницю між неперервністю і диференційованістю функції, довів кілька теорем про тригонометричні ряди, створив один з найбільш ефективних методів наближеного розв’язування алгебраїчних рівнянь.  

Лобачевський помер, так і не дочекавшись визнання своїх ідей. Лише Гаусс висловив своє захоплення науковим подвигом російського вченого: він домігся призначення того членом-кореспондентом Геттінгензького королівського наукового товариства. Хоча в Росії Лобачевський дослужився до високих чинів, був нагороджений великою кількістю орденів, був шанований ученими, але про його геометрію воліли не говорити. Після його смерті минуло понад двадцять років, коли геометрія Лобачевського здобула права громадянства в математиці.

А в XX ст. було виявлено, що геометрія Лобачевського має велике значення не тільки для абстрактної математики, але й безпосередньо пов’язана з використанням математики у фізиці. З’ясувалося, що взаємозв’язок простору і часу відкритий у працях Лоренца, Пуанкаре, Ейнштейна про який йдеться у спеціальній теорії відносності, має безпосереднє відношення до неевклідової геометрії. Наприклад, при розрахунках сучасних синхрофазотронів використовуються формули геометрії Лобачевського.

Неевклідова геометрія стала найбільшим інтелектуальним здобутком XIX століття. Вона ясно продемонструвала, що до математики не можна ставитися як до зведення незаперечних істин. У найкращому разі вона може гарантувати вірогідність доведення на основі недостовірних аксіом. Проте математики надалі дістали змогу досліджувати будь-які ідеї, які могли здатися їм привабливими. Кожен математик окремо був тепер вільний уводити свої власні нові поняття і встановлювати аксіоми на свій розсуд, стежачи лише за тим, щоб теореми, які випливають із аксіом, не суперечили одна одній. Грандіозне розширення кола математичних досліджень наприкінці минулого століття по суті стало наслідком цієї нової свободи дій.

 

Софія Василівна Ковалевська

(1850 – 1891 рр.)

 

В історії людства до Ковалевської не було жінки,

рівної їй за силою і своєрідністю математичного таланту.

                                       С. І. Вавилов

 

 

 

 

 

 

 

 

 

 

Софія Василівна Ковалевська – російський математик, перша в світі жінка – професор і член-кореспондент Петербурзької академії наук. Народилась в Москві, в сім’ї артилерійського генерала В. Корвін-Круковського. З раннього дитинства Софія захоплювалася читанням літератури і наукових книг. Батьки мало цікавились її вихованням. Значний вплив на Софію надав її дядько – Петро Васильович. Він не був математиком, але прочитав багато математичних книг, і любив розказувати Софії про різні питання математики. Його захоплення передалось і племінниці. Але перше знайомство з математикою відбулося коли їй було 8 років. Для обклеювання кімнат не вистачало шпалер, і стіни кімнати маленької Соні обклеїли листами лекцій Остроградського по математичного аналізу. Вона згадувала: «Від довгого щоденного споглядання зовнішній вигляд багатьох формул так і врізався в моїй пам’яті…» Математичні здібності Ковалевської проявились вперше в 13 років. Захоплення математикою у Ковалевської було настільки сильним, що вона забувала про все. Але в ті часи жінки не мали права навчатися в університетах Росії. Вищу освіту вона могла отримати лише за рубежем, але для поїздки вимагалось, щоб жінка була заміжньою. В 18 років Софія виходить заміж за відомого палеонтолога Ковалевського. В 1869 році молоде подружжя їде в Германію. З великими труднощами їй вдалось поступити в Гейдельберзький університет, де вона слухала лекції по вищій математиці, фізиці та інших науках. Але Ковалевська прагнула в Берлінський університет, одним із професорів якого був видатний математик Карл Вейєрштрасс. Оскільки в Берлінський університет жінки не мали доступу, Ковалевська відправилась додому до Вейєрштрасса з просьбою займатися з нею індивідуально. Вейєрштрасс запропонував їй розв’язати кілька досить складних задач. Ковалевська швидко їх розв’язала, і Вейєрштрасс, переконавшись в видатних здібностях своєї відвідувачки, погодився займатися з нею.

В липні 1874 року Вейєрштрасс представляє три роботи своєї учениці в Геттингенський університет для присвоєння ступеня доктора філософії, підкреслюючи, що для отримання ступеня достатньо будь-якої з цих робіт. Причому дві з них були із області математичного аналізу. В них були викладені питання теорії гіроскопа, необхідні для розрахунків стійкості корабля. Третя робота відносилась до астрономії. В ній розглядалось питання про кільця Сатурна. Ступінь Ковалевській було присуджено «з вищою похвалою».

Повернувшись в Росію, Ковалевські поселились в Петербурзі. На батьківщині Ковалевська не могла знайти застосування своїм знанням: жінкам наукова кар’єра була закрита. Оскільки Софія Василівна відрізнялась різносторонньою освітою, вона почала займатись літературою і публіцистикою, розміщувала в різних газетах і журналах наукові огляди, театральні рецензії та інші статті. Вона зустрічається   з Достоєвським, здружилась з Тургенєвим. Її цікавить розвиток подій в країні. Переїхавши з чоловіком в Москву, Ковалевська намагалась здати магістерський екзамен. Але царський міністр освіти  відмовив Ковалевській, відмітивши при цьому, що вона і її дочка «встигнуть зістаритися, перш ніж жінки будуть допущені до університету».

Важким для Ковалевської виявився 1883 рік. Втягнутий в фінансові операції одним нафтопромисловцем, покінчив із собою Ковалевський. І Софії прийшлось багато попрацювати, щоб повернути добре ім’я чоловіка.

Ковалевська змушена з дочкою виїхати в Швецію, і починає працювати в Стокгольмському університеті, де через рік стає професором. На протязі 8 років вона прочитала 12 курсів лекцій. Багато студентів і викладачів з любов’ю  називали її «наш професор Соня».

Софія Василівна не обмежувалась тільки викладацькою діяльністю. Вона систематично читає наукові журнали на російській, німецькій, французькій мовах. Приймає саму активну участь в обговоренні питань про становище жінки в суспільстві. Вона була одним з редакторів відомого математичного журналу під латинською назвою «Акта математика» (математичні відомості), займалась серйозними науковими дослідженнями, захоплювалась літературною діяльністю, писала романи, вірші, драми. Багатьом здавалось дивним, як вона поєднує математику з поезією. Сама ж Ковалевська писала: «Більшість, кому ніколи не приходилось більш глибоко пізнати математику, змішують її з арифметикою і вважають наукою сухою. А це наука, яка потребує найбільше фантазії, і один з перших математиків нашого століття говорить цілком справедливо, що не можна бути математиком, не будучи в той же час поетом в душі. Мені здається, що поет повинен бачити те, чого не бачать інші, бачити глибше від інших. І це саме повинен і математик.

Щодо мене, то я все моє життя не могла вирішити: до чого в мене більше нахилу – до математики чи до літератури».

Найважливішою науковою роботою Ковалевської було повне розв’язання задачі про обертання твердого тіла навколо нерухомої точки. За цю роботу їй була присвоєна в 1888 році премія Паризької академії наук. Софія Василівна стала знаменитістю. Англійський математик Дж. Сильвестр написав в її честь сонет, в якому назвав її «небесною музою». Завдяки старанням великого російського математика П. Л. Чебишова Петербурзька академія наук обрала Ковалевську своїм почесним членом-кореспондентом. Про неї писали газети і журнали всього світу. Не дивлячись на успіхи, Ковалевська відчувала себе самотньою на чужині і сумувала за батьківщиною. Вона все життя мріяла про те, щоб викладати, працювати у себе на батьківщині, але навіть після її наукових успіхів в царській Росії для неї місця не знайшлося. В останні роки свого життя Ковалевська здружилась зі швецькою письменницею Еллін Кей і знову захопилась літературною діяльністю. В кінці січня по дорозі із Франції до Швеції вона сильно застудилась і захворіла запаленням легень, 10 лютого 1891 року в повному розквіті творчих сил Ковалевська померла.      

Про Софію Ковалевську написано чимало книг і статей. Наукові праці Ковалевської, які виявились важливим внеском в світову науку і прославили російське ім’я, не втратили своєї цінності і в даний час. Образ Софії Ковалевської, талановитої жінки-математика, яка в роки темної реакції з незвичайною сміливістю і наполегливістю пробивала собі дорогу в науку і світ, ще довго буде викликати захоплення передових людей всього світу.

Перше кохання

Це сталося вперше, коли Софії виповнилося 13 років. Саме тоді вона закохалася. У ... письменника Федора Михайловича Достоєвського.

Анюта була старша за Софію на шість років. До 15-ти років перечитала всю батьківську бібліотеку. В той час, як Софія займалася зі своїми вчителями, Анюта вже вважалася до рослою панянкою. Байдикуючи і тиняючись по садибі, не знаючи, чим зайнятися, вона почала писати повісті. Потай від батьків Анюта відправляла їх поштою до Петербурга видавцеві журналу "Епоха" Федору Михайловичу Достоєвському. Повісті були прийняті і опубліковані, і секрет Анюти був розкритий.

Був гучний скандал. Батько сімейства не любив жінок-письменниць і вважав це заняття ганьбою для дівчини з пристойної сім'ї. Однак, після прочитавши повісті "Сон", він трохи пом'якшав і дозволив Анюті познайомитися з Достоєвським. Знаючи про те, що Достоєвський був п'яницею і завзятим картярем, він наказав матері ні на хвилину не залишати їх наодинці.

Чотирнадцятирічна Софія теж випросила дозволу бути присутньою при цій зустрічі. Для неї знайомство з відомим письменником уявлялося чимось неймовірним. Ще б, такий великий чоловік раптом виявиться у них в будинку, буде сидіти поруч в старому оксамитовому кріслі і пити чай з улюбленої маминої чашечки з блакитними волошками!

Гарячково перебираючи сукні в своїй шафі, вона не знала в чому з'явитися перед ним. За годину до його приходу вона, із завмиранням серця, стала прислухатися до кожного дзвінку в передній. Перша зустріч пройшла невдало. У своїх "Спогадах дитинства" Софія напише "Федору Михайловичу ... було досить ніяково і незатишно в цій натягнутій обстановці. Він і конфузився серед цих старих пані, і злився. Він здавався в цей день старим і хворим, як завжди, втім, коли бував не в дусі. Він весь час нервово пощипував свою рідку борідку і кусав вуса, причому все обличчя його пересмикувалось".

Нарешті Федір Михайлович узяв шапку, вклонився якось ніяково і квапливо пішов.

Ніхто не очікував побачити Достоєвського знову. Однак, за п'ять днів він прийшов знову. Заставши вдома одних сестер, він розвеселився. На цей раз теми для розмови знаходилися самі собою. Анюта і Федір Михайлович сиділи поруч, жартували і сміялися. Софія мовчала. Не зводячи очей з Достоєвського, вона боялася втратити хоча б одне слово.

Тепер перед нею була зовсім інша людина, не той, якого вона побачила в перший раз. Цей був молодий, ввічливий і розумний чоловік. Їй здавалося, ніби вони знайомі багато років. "Невже йому вже 43 роки! - З подивом думала вона. - Невже він в три з гаком рази старший за мене і більше ніж в два рази старший за сестру! Та при тому ще великий письменник: з ним можна бути зовсім як з товаришем".

З цього дня Федір Михайлович став часто бувати у Корвін-Круковських. Особливо подобалися Софії ті вечори, коли, крім нього, не було інших гостей. Достоєвський пожвавлювався і починав розповідати зміст задуманих ним романів. Він говорив пристрасно, поривчасто, чим заворожував Софію. Вона сиділа з розширеними від подиву і захвату очима, ковтаючи кожне слово, кожну деталь розповіді. Увечері, лягаючи спати, вона з посмішкою згадувала все, про що він говорив, і пошепки повторювала фрази, які найбіль запам'яталися.

Незабаром відносини Анюти і Достоєвського зіпсувалися. Він нервував і чіплявся до Анюти, яка із задоволенням піддражнювала його. Достоєвський брав капелюха і йшов, урочисто оголошуючи, що більше ноги його не буде в цьому будинку. Але наступного дня він знову приходив, як ніби нічого не сталося.

Бажаючи подражнити Анюту, Достоєвський часто ставив Софію в приклад сестрі "Інша справа ваша сестра! Вона ще дитина, а як розуміє мене! Тому що у неї душа чуйна!"

Софія вперше чула такі похвали від чоловіка. Вона раділа, що подобається письменникові. Не в силах нічого вдіяти з собою, вона раділа кожен раз, коли Анюта і Достоєвський сварилися. Їй було приємно, що він із захватом відгукується про її зовнішність.

Софія була зачарована Достоєвським. "Господи, нехай хоч весь світ захоплюється Анютою, - шепотіла вона. - Зроби тільки так, щоб Федору Михайловичу я здавалася найгарнішою".
 Однак, Господь не почув її. І незабаром знаменитий письменник освідчився старшій сестрі.

Дізнавшись про це, Софія довго не розмовляла з Анютою. Тому не одразу взнала, що та відкинула пропозицію письменника. Перше кохання минуло досить швидко. Софія вилікувала себе заняттями математикою.

Фіктивний шлюб - шлях до свободи

Під впливом Достоєвського сестри захопилися прогресивними ідеями. Вони вирішив продовжити навчання за кордоном, де жінки могли отримати вищу освіту.

Однак батько, прихильник традиційного способу життя, не хотів бачити дочок емансипованими інтелектуалками.

Тоді винахідлива Анюта придумала, яким чином вирватися з-під батьківської опіки "Потрібно фіктивно вийти заміж, тоді батько відпустить мене з чоловіком хоч на край світу, і ти поїдеш з нами".

Незабаром кандидат на роль чоловіка був знайдений. Ним виявився знайомий сестер - сусід і дворянин Володимир Онуфрійович Ковалевський, розумний і освічений чоловік. Він володів книжковим видавництвом, де видавалися солідні наукові праці.

І коли Анюта запропонувала Володимиру фіктивний шлюб, той відповів, що готовий одружитися, але ... тільки на Софії. Він давно звернув увагу на молодшу з сестер. Йому подобалися її розважливість і захопленість наукою в свої 18 років.

Однак батьки раптом вирішили, що молодшій сестрі непристойно виходити заміж раніше за старшу. Розуміючи, що їх план під загрозою, Софія знайшла рішення. Одного разу ввечері вона втекла до Володимира, заявивши батькам, що нікуди від нього не поїде. Скандал вдалося зам'яти, і молоді повінчалися, а через рік разом з Анною виїхали закордон.

Спочатку Ковалевські з Анютою відправилися до Відня, але там не було хороших математиків, і Софія наполягла на тому, щоб переїхати до Гейдерберга. Однак професора місцевого університету довго вагалися: давати їй дозвіл відвідувати лекції чи ні. Адже перш жінки не допускалися до вивчення фізики і математики. Але Софія була наполегливою, і професори вирішили зробити виняток.

Поки ж Софія штудіювала німецьку і відвідувала лекції, Анюта відверто нудьгувала. Їй, як письменниці, потрібні були нові яскраві враження. І тоді вона вирушила до Парижа, де незабаром, покохав, вийшла заміж за майбутнього героя паризької комуни Віктора Жеклара.

А у Володимира Ковалевського, який мріяв вивчати поліантологію, все складалося не найкращим чином. Незважаючи на те, що шлюб їх вважався фіктивним, Софія вимагала постійної уваги. Гельдерберг її вже не влаштовував. "Роби, як хочеш", - написав він їй. І Софія вирішила переїхати до Берліна.

Початок математичної кар'єри

Бути ученицею всесвітньо відомого математика Карла Вейєрштрасса. Складно сказати, на що розраховувала 20-ти річна Софія Ковалевська, ймовірно, на диво. Тому що професор Вейєрштрассе принципово не брав в учні жінок.

Але, на щастя, він був джентльменом, тому, запросивши Софію прийти, вручив їй кілька дуже складних завдань і був упевнений, що відвідувачка більше не з'явиться.

Однак, коли через тиждень Софія прийшла до нього знову, Вейєрштрасса довго не міг прийти до тями від подиву - адже ця миловидна росіянка знайшла свої оригінальні рішення.

Дивлячись на юну худеньку дівчину, яка трималася просто й природно, великий математик розтанув. А коли Софії не дозволили відвідувати Берлінський університет, він запропонував їй займатися у себе на квартирі. Під його керівництвом Софія написала свою першу наукову роботу "До теорії диференціальних рівнянь в частних похідних", яка викликала захоплення вчених.

З Володимиром в той період вона майже не бачилася. Коли він приїжджав до Берліна, все закінчувалося сварками. Її дратувало, що він чудово обходиться і без неї. Займається палеонтологією, їздить у експедиції. Однак Софія розуміла, що якщо вона кине математику, це потішить Володимира, але розіб'є серце професору Вейєрштрассе. Адже завдяки йому Софія стала доктором філософії з математики.

Однак робота на знос коштувала їй здоров'я. І Софія явно відчула свою самотність і тугу за батьківщиною. Треба повертатися до Росії, там вона відновить сили, тим більше що її дуже чекала сестра Анна, яка до того часу повернулася з Франції разом з чоловіком і сином. Як же Софія скучила за сестрою! Може Анна зі своїм простим життєвим досвідом допоможе їй вирішити головну задачу - як стати щасливою.

Чи легко бути жінкою?

Приїхавши до Петербурга, Софія тут же виявила бажання викладати в університеті. Їй відмовили. "Ви жінка, - сказав їй один з чиновників, - а у нас викладають тільки чоловіки і нам не треба ніяких нововведень". На що Софія різко відповіла: "Коли Піфагор відкрив свою знамениту теорему, він приніс у жертву богам 100 биків, з тих пір всі скоти бояться нового".

Це був виклик. Їй запропонували місце вчительки початкових класів жіночої гімназії. "На жаль, я не дуже тверда у таблиці множення", - сказала вона і поїхала в родовий маєток Полібіно.

Після її приїзду раптово помер батько. Софія була вражена. Але ця смерть змусила її по-іншому поглянути на її відносини з чоловіком. Вона відчула себе маленькою, незахищеною. І коли Володимир повернувся в Росію, їх шлюб перестав бути фіктивним.

Софія тоді припинила цікавитися математикою, тісно зійшлася з гуртком літераторів і навіть написала роман "Приват доцент", який був сприятливо зустрінутий критиками.

Однак, богемний спосіб життя вимагав чималих витрат, і тоді Софія запропонувала чоловікові зайнятися комерцією. А в якості початкового капіталу використовувати спадщину, залишену їй батьком.

Ось тут в її дії і закралася помилка, яка стане ще одним кроком на шляху до трагедії. Ковалевські побудували в Петербурзі кілька багатоповерхових будинків для здачі в найом, банк і оранжерею. Взяли участь у видавництві нової газети.

Друзі пророкували їм блискуче майбутнє. А їх дочку навіть називали багатою спадкоємицею. Однак Володимир виявився поганим комерсантом. І незабаром все майно Ковалевських перейшло до кредиторів.

Як не дивно, але Софія легко перенесла цю сумну новину на відміну від Володимира, а який у всьому винив одного себе. Ще вчора він був вченим із світовим ім'ям, видатним палеонтологом! А тепер не вчений, не комерсант - усе розвалилося. І скільки дружина не намагалася зацікавити його наукою - все було марно.

А потім до неї стали доходити чутки, що Володимир захопився якоюсь жінкою. Це рівняння з новим невідомим Софія вирішила швидко. Влаштувавши сцену ревнощів, кинувши дочку на піклування подруги, виїхала до Берліна.

Вона помилилася. Вирішувати задачу про щастя виявилося важче, ніж вона думала.

Нерозв'язна задачка

Професор Вейєрштрассе зустрів Софію словами: "У мене для тебе є нове завдання, за яке не беруться навіть видатні математики. Це завдання про обертання твердого важкого тіла навколо нерухомої точки. Упевнений, цей горішок тобі по зубах".

І Софія зайнялася обчисленнями. Адже якби їй вдалося вирішити цю задачу, механіки її теж назвали б видатним математиком.

Але робота йшла настільки повільно, що навіть через два роки Софія майже не просунулася ні на крок.

Крім того, вона явно була у злиднях. І друзі поклопотали про те, щоб її запросили читати лекції в Стокгольмському університеті.

Однак Софія була так замучена морально і фізично, що панічно боялася виступати публічно.

І замість того, щоб відправиться до Швеції, поїхала до Парижа. Їй хотілося розвіятися, відволіктися від переживань.

Софія з головою поринула у вир світського життя. На якусь мить їй здалося, що вона знайшла вірний засіб від меланхолії.

Але, на жаль, це знову була помилка. Вона зрозуміла це надто пізно, коли з Росії прийшла страшна звістка. Володимир Ковалевський, якого оголосили банкрутом, покінчив життя самогубством.

На п'ятий день голодування Софія втратила свідомість. Прокинувшись, стала записувати якісь математичні викладки, через кілька днів дала згоду читати лекції в Стокгольмському університеті. А ще через місяць, забравши з Росії дочку, переїхала до Швеції. У той час їй було 33 роки.

У Париж Софія повернулася лише 3-ма роками потому. І все тому, що весь цей час панічно боялася цього міста, адже саме тут її наздогнала звістка про загибель чоловіка. Тут же очікувала її нова трагічна звістка.

Вона їхала сюди вже професором Стокгольмського університету. Її життя стало потроху налагоджуватися. Але раптом смертельно захворіла сестра Анюта. Найрідніша і найближча людина. Ниточка, що пов'язувала її з батьківщиною, з минулим, з дитинством, таким світлим і безтурботним.

Софія тут же помчала до Петербурга. І там, сидячи біля ліжка вмираючої сестри, раптом замислилася. А адже їх життя могло скластися зовсім інакше. Як було і як могло бути. Саме тоді в Петербурзі Софія вирішила написати драму з двох частин. У першій всі герої робляться нещасними, а в другій, навпаки, щасливими.

Ця книга була написана спільно зі шведською письменницею Едглер де Флер. І побудована була за чисто математичними законами. Вона вклала в цей роман всі свої думки, переживання. А в образі головної героїні вивела себе.

Після смерті Анни у Софії не залишилося жодної близької людини, крім дочки. Тоді вона навіть не підозрювала, що через рік доля пошле їй зустріч, на яку вона чекала все життя.

Нове кохання і заслужене визнання

За іронією долі він носив таке ж прізвище, як і її покійний чоловік - Ковалевський. Був видатним соціологом, юристом.

Вів себе із Софією вельми наполегливо. Але підкорив її серце після одного випадку.

Одного разу в ресторані Софія перекинула на себе келих вина і засмутилася через зіпсоване вбрання. На наступний ранок Максим Максимович Ковалевський з'явився до неї з коробкою, в якій була сукня як дві краплі води схожа на вчорашню. Як йому вдалося дістати точно таку ж, причому за одну ніч, так і залишилося для Софії загадкою. Зустріч з Ковалевським допомогла їй знайти душевний комфорт.

І Софія, нарешті, закінчила дослідження тієї самої важкої задачі, яку їй доручив професор Вейєрштрассе, і яку не змогли вирішити такі великі математики як Ейлер і Лагранж.

Работа була надіслана на конкурс в Паризьку академію наук і виграла престижну премію Бордена, яка три роки поспіль ні кому не присуджувалася. Вона стала в ряд перших математиків світу.

Максим Ковалевський був свідком її тріумфу. А їй хотілося тільки одного - залишитися з ним наодинці.

Якою незначною здавалася їй надважка математична задача, яку вона вирішила, поряд з іншим завданням - стати щасливою.

Наступного року, за роботу на ту ж тему, Софія Ковалевська була удостоєна премії, цього разу шведської академії наук.

Крім того, Софію нарешті визнали і на батьківщині. І обрали членом-кореспондентом російської академії наук. "Наша академія наук тільки що обрала вас, Софія Василівна, членом-кореспондентом, допустивши цим нововведення, якому не було досі прецеденту", - писав їй відомий вчений Чапішев.

І ще Максим зробив Софії офіційну пропозицію. "Вам навіть прізвище міняти не доведеться", - пожартував він.

Однак самій Софії було вже не до сміху. Серцем вона бажала бути з коханою людиною, але от розумом вона боялася, що знову доведеться обирати між математикою і сімейним життям. Тоді Софія не дала Максиму ніякої відповіді, вона не могла зробити щасливою кохану людину і при цьому не втратити саму себе.

Вона відчувала, що в даному випадку математика їй не допоможе. І Софія стала заносити на папір все те, що було їй пережито за минулі роки. Мемуари, спогади про дитинство були визнані кращим твором Ковалевської.

Новий рік на кладовищі

Однак і заняття літературою не допомогли їй прийняти рішення. І в той самий момент, коли Софія зовсім зневірилася, з Петербурга прийшла звістка. У Російській академії з'явилося вакантне місце на кафедрі математики.

І Софія помчала до Петербурга, сподіваючись отримати це місце. Але, на жаль, закулісні ігри не дозволили їй стати першою в історії жінкою-академіком. Ніхто не став навіть розглядати її заяву. Їй навіть заборонили бути присутньою на засіданнях академії.

Вона знову повернулася до Стокгольу. Розбита, пригнічена, розчарована.

Максим, який втомився від невизначеності в їх відносинах, поставив їй умову: або ми разом, або розходимося назавжди. І знову, якимось неймовірним чином, Софії вдалося втекти від решенія.

1891 рік вони з Максимом зустрічали разом в Генуї. Гуляючи, не помітили, як заблукали на кладовищі. "Знаєш, хтось із нас не переживе цього року, недарма ми зустріли новий рік на кладовищі".

Через кілька тижнів він проводив її на поїзд, який прямував до Стокгольма. По дорозі через різку зміну клімату Софія застудилася.

Повернулася до Швеції вже хворою. Лікар поставив діагноз: запалення легень. Друзі чергували біля її ліжка цілу добу.

В одну з ночей, коли вона міцно заснула, всі вирішили, що справа йде на поправку. Тієї ж ночі Софія Ковалевська померла від паралічу серця.

Її останніми словами були "Занадто багато щастя ..."

Відспівували Софію Василівну в Свято-Преображенському храмі - найстарішій російській православній церкві в Західній Європі, а жалобний катафалк до кладовища проводжали тисячішведів. Телеграми і вінки надходили з Росії та інших країн, всі шведські газети помістилижалобні некрологи.

Через п'ять років на кошти російських жінок С. В. Ковалевської був поставлений пам'ятник відвдячних співвітчизниць.

До самої своєї кончини в 1916 році Максим Ковалевський не міг забути Софію Василівну. Листи їїМаксим Максимович перед смертю залишив своєму племіннику. На жаль, вони пропали ...

Її дочка, яка в 13 років залишилася круглою сиротою, невдовзі повернулася в Росію. Стала лікарем. Вона померла в Москві у віці 74 років, так ніколи не вийшовши заміж.

 

 

 

 

 

 

 

Андрій Миколайович Колмогоров

(1903 – 1987 рр.)

 

Займаючись з деяким успіхом, а іноді й з користю, досить

широким колом практичних застосувань математики, я

залишаюсь в основному чистим математиком. Захоплююсь

математиками, які перетворились у видатних представників

нашої техніки.

                                    А. М. Колмогоров

 

 

 

 

 

 

 

 

 

 

 

Андрій Миколайович Колмогоров – видатний математик. Народився в Тамбові. В 1925 році закінчив Московський університет, а з 1930 року – професор того ж університету, з 1935 року – доктор фізико-математичних наук.

Наукову діяльність Колмогоров розпочав в області теорії функцій дійсної змінної, де відомі його праці по збіжності тригонометричних рядів, теорії міри, узагальненню поняття інтеграла й загальній теорії операцій над множинами. В 1956 році отримав важливі результати по представленню функцій декількох змінних функціями меншої кількості змінних, зокрема він довів, що функції чотирьох і більше змінних можна звести до функцій трьох змінних. В 1957році його учень В. І. Арнольд вирішив тринадцяту проблему Д. Гільберта, відкинув ствердження про те, що функцію трьох змінних не можна звести до функцій двох змінних, а Колмогоров показав, що функцію двох змінних можна звести до функцій однієї змінної. Колмогоров зробив суттєвий внесок в розробку так званої конструктивної логіки; в топології створив теорію верхніх чи V-гомологій. Важливі труди Колмогорова відносяться також до теорії ймовірностей, де він разом з О. Я. Хінчиним почав (1925) застосовувати методи теорії функцій дійсної змінної, що дозволило розв’язати ряд важких проблем і побудувати широко відому систему аксіоматичного обумовлення теорії ймовірностей. З початку 1930-х років в працях Колмогорова переважають аналітичні методи, застосування яких допомогло створенню теорії марківських процесів з неперервним часом. Вченому належать також дослідження по теорії стрільби, по статистичних методах контролю масової продукції і теорії передачі інформації по каналах зв’язку. В 1965 році Колмогоров разом з Арнольдом удостоєний Ленінської премії за цикл робіт по проблемі стійкості гамільтонівських систем. Колмогоров приймає активну участь в розробці питань викладання математики в школі; являється автором багатьох шкільних підручників з математики. Займається вчений також питаннями історії математики, філософії. Ім’я Колмогорова зустрічається в різних галузях математики. Наприклад, в теорії функцій дійсної змінної відомі інтеграл Колмогорова, критерій для полінома найкращого наближення, нерівності; в теорії ймовірностей – Колмогорова нерівність і рівняння; в математичній статистиці – критерій Колмогорова. Вчений опублікував понад 230 робіт, створив велику школу в області теорії функцій і теорії ймовірностей. Колмогоров писав: «Помилковим є уявлення про математику як про науку викінчену, раз назавжди побудовану в своїх теоретичних основах. Насправді математика збагачується цілком новими теоріями й перебудовується у відповідь на нові запити механіки (нелінійні коливання, механіка надзвукових швидкостей), фізики (математичні методи квантової фізики) та інших суміжних наук».Серед його учнів – А. І. Мальцев, Ю. В. Прохоров, Б. В. Гнєденко, В. І. Арнольд, Ю. А. Розанов.

 

 

 

Олексій Васильович Погорєлов

(1919 – 2002 рр.)

Олексій Васильович Погорєлов – радянський математик, заслужений діяч науки і техніки України, почесний громадянин міста Харків, лауреат Державної премії СРСР. Народився в Корочі. Інтерес до математики з’явився у Погорєлова з 13-14 років у зв’язку з успішним виступом на математичних олімпіадах для школярів в роки навчання в середній школі №80, що і нині знаходиться на вулиці Другої П’ятирічки міста Харкова. Це і визначило подальшу долю Олексія Васильовича. У 1937 році він стає студентом фізико-математичного факультету Харківського університету, а у 1941 році в зв’язку з початком Великої Вітчизняної війни його було призвано до армії і направлено до Військово-повітряної академії ім. Жуковського. Закінчивши академію (1945), працював в Центральному аерогідродинамічному інституті (ЦАГІ) і одночасно навчався в аспірантурі Московського університету. З 1947 року працював в Харківському університеті. В 1959–1960 роках працював в Інституті математики АН УРСР. З 1960 року Олексій Васильович став працювати в тільки що заснованому у Харкові фізико-технічному інституті низьких температур. Тут талант вченого розкрився з новою силою.

Основний напрямок математичних досліджень Погорєлова – питання геометрії в цілому. В циклі праць він дав повний розв’язок проблеми однозначної визначеності для загальних опуклих поверхонь, довів рівність замкнутих ізометричних опуклих поверхонь, рівність нескінченних опуклих поверхонь з повною кривизною 2 та рівність нескінченних опуклих поверхонь з кривизною, меншою, ніж 2, при деяких додаткових умовах. За праці з теорії опуклих поверхонь Погорєлову була присвоєна Державна премія СРСР (1950).

В 1959 році  Погорєлов повністю розв’язав проблему нескінченно малих вигинів загальних опуклих поверхонь. Вчений довів теорему існування узагальнених розв’язків рівняння Монжа – Ампера загального вигляду, теорему про єдність узагальнених розв’язків. За праці, написані в 1956 – 1960 роках Погорєлову була присвоєна Ленінська премія (1962). З 1960 року Погорєлов значну увагу приділяє механіці. Результати цих досліджень викладені в монографії «Геометрична теорія стійкості оболонок»(1966). Погорєлов видав багато підручників для університетів з різних розділів геометрії. В 1982 році в масову школу був уведений підручник Погорєлова з геометрії і дотепер він є діючим у багатьох регіонах колишнього СРСР.

В Фізико-технічному інституті низьких температур імені Вєрніна Національної Академії Наук України Олексій Васильович працював до переїзду в Москву у 2002 році де і помер 17 грудня.

Першокласні підручники Погорєлова для вузів і середньої школи як і вся його науково-педагогічна спадщина увійшли в скарбницю світової науки і продовжують служити людям.

 

Практична частина

Позакласний захід.

Тема: «Рене Декарт – людина та вчений».

Мета: розширити знання учнів про видатних вчених; розвивати пізнавальний інтерес; виховувати прагнення до безперервного вдосконалення своїх знань; творчо мислити, здобувати знання, швидко орієнтуватися в навколишній обстановці, знаходити правильну відповідь, працювати в команді.

Стимулювати активну творчу роботу школярів, розвивати логічне мислення, кмітливість, уміння діяти в нестандартних ситуаціях; виховувати цілеспрямованість.

Обладнання: презентація, відеофільм, картки – вислови, картки вікторина.

План:

1. Вступ.
2. Доповідь учнів.
3. Філософія Рене Декарта: завдання – вислови.

     ІV. Підведення підсумків. Вікторина.

І. Вступ.

1-й ведучий.

Увага! Увага!

Послухайте нас!

Цiкаву новину

Повідати час.

2-й ведучий.

А хто ще не встиг

Науки точні полюбити,

Ми з тим збираємось мiцно дружити.

Бо поведемо всiх по дорозi до знань:

Обчислень, задач, вікторин та рiвнянь.

1-й ведучий.

Науки ці нам треба добре знати,

Щоб професією вивчати

2-й ведучий.

Наука – знайдені алмази,

Вугілля, золото і мідь,

В руках людей могутній лазер

І сотні скошених угідь.

1-й ведучий.

Наука нам допомагає

Ракети в космос запускати

І будувати всюдиходи,

Щоб грунт на Місяці вивчати.

2-й ведучий.

До різних ми наук охочі.

Нехай ведуть нас до вершин,

А зараз ми сказати хочем

« Наш математиці уклін!»

Наука МАТЕМАТИКА

Я – математика, хоча суворою буваю,

Та я усе на свiтi знаю.

Що помножить, як вiднять,

Подiлити як, додать.

У цьому всьому я лад знайду

І не дам потрапити в біду.

Нехай мій парус далеко пливе

Вивчайте, вивчайте, вивчайте мене!

1-й ведучий.

Також до нас завітла друга цариця,

Математики сестриця

2-й ведучий.

Гей, нумо,  друзі,  в тісному крузі

Фізику ми прославляймо,

І на цьому уроці

Ії величність зустрічаймо

Наука ФІЗИКА.

Формули точні, мудрі закони

Завжди на службі людині.

Я із вами в навчанні і вдома

Кожної ночі і  днини.

Мчать по орбітах   всі  електрони,

Яблука падають в трави.

І хоч ми з вами ще не Ньютони,

Фізику вивчим на славу.

IІ. Витупи учнів з підготовленими доповідями.

Математика

«Міркування про метод». У 1637 побачила світ головна математична праця Декарта«Міркування про метод» (повна назва: «Міркування про метод, що дозволяє направляти свій розум і відшукувати істину в науках»). У цій книзі викладалася аналітична геометрія, а в додатках — численні результати в алгебрі, геометрії, оптиці (у тому числі — правильне формулювання закону заломлення світла) і багато чого іншого). Особливо слід відзначити перероблену Декартом математичну символіку Вієта, з цього моменту близьку до сучасної. Коефіцієнти він позначав a, b, c, а невідомі — x, y, z. Натуральний показник степеня прийняв сучасний вигляд (дробові і негативні утвердилися завдяки Ньютону). З'явилася риска над підкореневим виразом. Рівняння приводяться до канонічної форми (у правій частині — нуль). Символічну алгебру Декарт називав «Загальною математикою» і писав, що вона повинна пояснити «все, що відноситься до порядку і міри». Створення аналітичної геометрії дало змогу перевести дослідження геометричних властивостей кривих і тіл на алгебраїчну мову, тобто аналізувати рівняння кривої в деякій системі координат. Цей переклад мав той недолік, що тепер треба було акуратно визначати справжні геометричні властивості, які не залежать від системи координат (інваріанти). Однак переваги нового методу були винятково великі, і Декарт продемонстрував їх у тій же книзі, відкривши численні положення, невідомі древнім і сучасним йому математикам.

У додатку «Геометрія» були дані методи розв'язання алгебраїчних рівнянь (зокрема геометричні та механічні), класифікація алгебраїчних кривих. Новий спосіб завдання кривої — за допомогою рівняння — був вирішальним кроком до поняття функції. Декарт сформулював точне «правило знаків» для визначення числа додатних коренів рівняння, хоча і не довів його. Декарт досліджував алгебраїчні функції (многочлени), а також ряд «механічних» (спіралі, циклоїди). Для трансцендентних функцій, на думку Декарта, загального методу дослідження не існує. Комплексні числа ще не розглядалися Декартом на рівних правах з дійсними, однак він сформулював (хоча і не довів) основну теорему алгебри: загальна кількість дійсних і комплексних коренів алгебраїчного рівняння дорівнює його степеню. Від'ємні корені Декарт за традицією іменував помилковими, проте об'єднував їх з додатними терміном дійсні числа, відокремлюючи від уявних (комплексних). Цей термін увійшов у математику. Втім, Декарт виявив деяку непослідовність: коефіцієнти a, b, c у нього вважалися додатніми, а випадок невідомого знака спеціально відзначався трьома крапками ліворуч. Усі невід'ємні дійсні числа, не виключаючи ірраціональних, розглядаються Декартом як рівноправні; вони визначаються як відношення довжини деякого відрізка до еталону довжини. Пізніше аналогічне визначення числа взяли Ньютон і Ейлер. Декарт поки ще не відокремлює алгебру від геометрії, хоча змінює їхні пріоритети; розв'язок рівняння він розуміє як побудову відрізка з довжиною, рівною кореню рівняння. Цей анахронізм був незабаром відкинутий його учнями, передусім — англійськими, для яких геометричні побудови — чисто допоміжний прийом. Книга «Метод» відразу зробила Декарта визнаним авторитетом у математиці й оптиці. Прикметно, що видана вона була французькою, а не латиною. Додаток «Геометрія» було, проте, тут же перекладено латиною і неодноразово видавався окремо, розростаючись від коментарів і ставши настільною книгою європейських учених. Праці математиків другої половини XVII століття відображають сильний вплив.

Фізичні дослідження Рене Декарта.

Фізичні дослідження відносяться головним чином до механіки, оптики і будови Всесвіту.

•                  Декарт ввів поняття «сили» (міри) руху (кількості руху), маючи на увазі під ним добуток «величини» тіла (маси) на абсолютне значення його швидкості, сформулював закон збереження руху (кількості руху), проте тлумачив його неправильно, не враховуючи, що кількість руху є векторною величиною (1664).
•                  Досліджував закони удару, вперше чітко сформулював закон інерції (1644).
•                  Висловив припущення, що атмосферний тиск зі збільшенням висоти зменшується.
•                  У 1637 вийшла у світ «Діоптрика», де містилися закони поширення світла, відбивання та заломлення, ідея ефіру як переносника світла, пояснення веселки.
•                  Декарт першим математично вивів закон заломлення світла (незалежно від Вілеброрда Снеліуса) на межі двох різних середовищ^. Точне формулювання цього закону дозволило вдосконалити оптичні прилади, які тоді стали відігравати величезну роль в астрономії та навігації (а незабаром і в мікроскопії)!.

У фізиці він сформулював закон збереження кількості руху, запровадив поняття імпульсу сили.

У 1637 побачила світ головна математична праця Декарта «Міркування про метод» (повна назва: «Міркування про метод, що дозволяє направляти свій розум і відшукувати істину в науках»).

У цій книзі викладалася аналітична геометрія, а в додатках — численні результати в алгебрі, геометрії, оптиці (у тому числі — правильне формулювання закону заломлення світла) і багато чого іншого). Основні закони механіки, за Декартом, мають такий вигляд:

1. Тіла за своєю природою позбавлені сили, тому ні одне з них не може змінити стану, в якому тіло перебуває: воно має певну конфігурацію та положення і перебуває в певному стані свого спокою та руху, поки зовнішня причина не здійснить у ньому зміни.

2. З першого закону випливає, що кожне рухоме тіло продовжує свій рух у тому ж напрямі, який лишається незмінним. Якщо тіло описує криву, то напрям змінюється в кожний момент, що може трапитись при постійному впливі якої-небудь зовнішньої причини. Незмінно однаковий напрям є пряма лінія. Тому всяке рухоме тіло саме по собі намагається продовжити свій рух по прямій лінії, а коли внаслідок зовнішньої причини рухається по колу, – то по дотичній до нього. Кожне тіло повинно зберігати свій стан руху, тому воно повинно намагатися рухатись уперед по прямій лінії, тому що всяке відхилення від неї може бути тільки наслідком зовнішніх причин.

3. Порожнього простору не існує, тому всяке рухоме тіло, яке намагається продовжувати свій шлях по прямій лінії, повинно зустрічатися з іншим тілом, з яким воно зіштовхується. Зіткнення відбувається в протилежному або в тому ж напрямку.

У цілому Декарт при зіткненні тіл нараховує сім випадків та відповідно до цього сім правил, згідно з якими повинна відбуватися зміна, яка випливає із зіткнення тіл.

Ці закони виводяться з припущення: 1) у різних тіл протилежні не рухи, а лише рух та спокій, тому серед рухомих тіл неможлива ніяка інша протилежність, окрім протилежності їхніх напрямків; 2) тіла, які зіштовхуються цілком тверді та міцні; 3) абсолютно не береться до уваги всяка дія довколишніх тіл, які можуть збільшити або зменшити рух тіл, які зіштовхуються. Декарт зі свого закону постійності імпульсу виводить і третій закон Ньютона (дія дорівнює протидії), але він трактує його як поодинокий випадок, а не поширює на всі види взаємодій.

Р.Декарта сміливо можна вважати і батьком-предтечею другого закону динаміки (другий закон Ньютона). Він ввів поняття імпульсу (кількості руху), а другий закон Ньютона і є якраз законом зміни імпульсу [5-7].

Із законів Декарта випливає, що тіла самі по собі не мають сили; оскільки вони повинні намагатися зберегти той стан, в якому перебувають, то мають силу опору; усі зміни в матеріальному світі випливають із зовнішніх причин, а тому будь-який рух повинен бути наданий за допомогою удару або поштовху; у матеріальному світі немає ніяких схованих причин, сил та якостей. Такою притаманною тілу та початковою силою є вага. Декарт заперечує її. Разом із вагою він повинен заперечувати й тяжіння та силу тяжіння: у цьому він відрізняється від Галілея та Ньютона. Через це він повинен заперечувати і центральні сили. Тобто закони небесної механіки він виводить із теорії вихорів (флюїдів), яка була модною як в ХVІІІ, так і в ХІХ століттях.

Свої погляди на природу світла Декарт виклав у "Трактаті про світло” та "Діоптриці”.

У "Трактаті про світло” Декарт пише про основні властивості світла:

1) поширюється в усі сторони навколо тіл, які світяться;

2) на всі можливі відстані;

3) миттєво;

4) звичайно, по прямих лініях, які називаються променями світла;

5) певні з цих променів, виходячи з різних точок, можуть збиратись в одну і ту ж точку;

6) виходячи з однієї точки, вони (промені) можуть розходитися в різні напрямки;

7) виходячи з різних точок та прямуючи до різних точок, промені можуть пройти через одну і ту ж точку, не заважаючи один одному;

8) але іноді, коли їхня сили значно відрізняється, промені можуть і заважати один одному;

9) напрям променів може бути змінений за допомогою відбивання або

10) заломлення;

11) їхня сила може бути збільшена або ж зменшена різними позиціями або якостями середовища, що передає ці промені.

Декарт помилився лише в третьому пункті: через 40 років після появи "Діоптрики” Олаф Рьомер встановив скінченність швидкості світла. Усі властивості світла він пояснював за допомогою своєї теорії вихорів. Слід відзначити, що теперішні уявлення про електромагнітну природу світла, включають і вихореву природу. Ну а пункт восьмий можна розглядати як перший вислів про сучасну нелінійну оптику.

Про природу кольорів він писав у "Метеорах”: "Природа кольору заключається лише в тому, що частинки тонкої матерії, які передають дію світла, намагаються з більшою силою обертатися, ніж рухатися по прямій лінії; таким чином, ті, які обертаються з більшою силою, дають червоне світло, з ще більшою, дають жовте...”.

Теорію кольорів він пояснював на основі дифузного відбивання та вперше пояснив природу райдуги. Пізніше Р.Гук висловив гіпотезу про розкладання білого світла на кольори, а І.Ньютон експериментально це підтвердив.

Першим Декарт опублікував і закон заломлення світла (закон синусів), який зараз називається законом В.Снелла (Снелліуса). Є свідчення, що В.Снелл опублікував своє відкриття в курсі лекцій, які він читав у Лейденському університеті в 1621-1622 рр. Я.Гоол, який був професором математики в Лейдені після В.Снелла, про праці останнього дізнався лише після того, як захотів перевірити роботу Декарта. Тому в листі до Костянтина Гюйгенса Гоол пише, що він вражений відкриттям обох учених. Снелл отримав цей закон із досліду, Декарт – із роздумів. На відміну від Стелла, Декарт із цього закону вивів багато наслідків. Найважливішим є той факт, що швидкість світла може бути скінченною. Це випливало з того, що він розкладав швидкість світла на дві складові, одна з яких змінювалася. Безперечним є факт, що на обох учених мав великий вплив Й.Кеплер, який близько підійшов до відкриття цього закону.

Саме в диспуті з Декартом про поширення світла в середовищах з різною густиною П.Ферма сформулював свій знаменитий принцип найменшого часу, що відіграв важливу роль у становленні сучасної фізики.

У тій же "Діоптриці” Декарт описує будову ока та суть процесу побудови зображення та його відчуття в оці. Цей опис покладений в основу сучасного уявлення про око та процеси, які там відбуваються. Тут же наведена методика шліфування гіперболічних поверхонь.

Силу свого методу Декарт демонструє в "Метеорах”. Тут уперше метереологія постає як окрема наукова дисципліна.

В галузі анатомії та біології можна відзначити те, що він сприйняв теорію кровообігу В.Гарвея та не сприйняв його ж робіт про роль серця. У цілому ж він розглядав людський організм як механічний автомат. Слід відзначити, що до цього повернулись у ХХ столітті при створенні кібернетики.

На публікацію праць Декарта великий вплив мала доля Галілея: у 1633 році був виданий папський вердикт про заборону його космологічних праць, які підтверджували геліоцентричну систему нашого світу. Через це свої роботи з космології Декарт і не поспішав публікувати. В листі до Мерсенна він писав, що деякі його праці будуть опубліковані після смерті, не раніше як через 100 років.

Вердикт на заборону праць Декарта був виданий у 1663 році, через 13 років після його смерті. Декартові це вже було всеодно. Але зерна, посіяні ним, дали щедрий урожай.

Наведемо ще одну цитату Декарта з його листа Бекману від 26 березня 1619 року: "... я намагаюся викласти зовсім нову науку, яка дозволила б загальним чином розв'язати усі проблеми незалежно від виду величини, неперевної чи дискретної, виходячи кожен раз із природи самої величини… Це не може бути праця одинака, та її ніколи не закінчать”. Саме намагаючись просунути цю працю якомога далі, тобто працюючи над проблемами створення універсального числення, Вільгельм Ляйбніц створив інтегро-диференційне числення та заклав основи синтезу математики та логіки. Очевидно саме тому, що основні космологічні та релігійні праці Декарта були заборонені, Ляйбніц, який добре знав науковий доробок Декарта, шукав нові сфери для доведення правоти методу свого вчителя, щоправда заочного (очним учителем був Х.Гюйгенс). Як бачимо, це йому цілком вдалося.

Трохи іншим шляхом, але також від Декарта, пішов Ісаак Ньютон. По-перше, він підійшов до проблеми не побудови, а обчислення дотичних до кривих. Так появився ньютонівський варіант математичного аналізу: метод флюксій та флюент. Але на відміну від Ляйбніца, який використовував методологію Декарта, Ньютон створив свою власну методологію, яка є практично синтезом методолoгії Декарта та Ф.Бекона.

Пізніше завдяки Х.Вольфу, І.Канту, Л.Ейлеру ця методологія була пов'язана з вимірюванням. Так зародилася сучасна фізика, математика та ряд інших наук. Саме шляхом оптимального дедуктивного синтезу була створена сучасна електродинаміка, термодинаміка, кібернетика, квантова теорія.

Подальше узагальнення декартових координат до узагальнених призвело до побудови аналітичної механіки та загальної теорії відносності. Кінематика ж – це взагалі тріумф застосування аналітичної геометрії Декарта. Узагальнення геометричного підходу Декарта призвело до появи нових векторних просторів, що дало життя таким розділам сучасної математики та фізики, як функціональний аналіз, аналітична механіка, статистична механіка, квантова механіка, алгебраїчна геометрія тощо. Можна розглядати і як тріумф картезіанства спеціальну та загальну теорії відносності.

Астрономія

«Кто первым высказал гипотезу о том, что Земля имеет раскаленное ядро?»

В астрономії Декарт відомий як автор космогонічної гіпотези — теорії вихорів, яка протягом певного часу конкурувала з теорією всесвітнього тяжіння. Вважав, що Сонце (як і інші зірки) оточене ефірною речовиною, яка розповсюджується на великі відстані у всіх напрямах. Обертаючись, Сонце приводить в обертальний рух прилеглі області цієї речовини, потім вони, у свою чергу, передають його наступним областям, так що, нарешті, вся маса приходить в обертання. У цьому ефірному вихорі мчать навколо Сонця планети. Проте Декарт не зміг сформулювати закони планетних рухів, тому його гіпотеза не отримала подальшого розвитку.

Філософське вчення Декарта на противагу середньовічним поглядам ґрунтувалося на уявленні про безмежність й однорідність світової матерії (простору), який не має порожнеч і нескінченно подільний.

ІІІ. Філософія Рене Декарта. Вислови.

Я знаю себе як думку, але я, безумовно, не знаю себе як мозок.

Боязливість дуже шкідливе тому, що вона утримує волю від корисних дій.

Повага інших дає привід для поваги самого себе.

Мало мати хороший розум, головне - добре його застосовувати.

Розум - це запальне скло, яке, запалюючи, саме залишається холодним.

Прагни перемагати швидше самого себе, ніж долю, і змінювати своє бажання, ніж порядок у світі.

Здоровий глузд – найбільш розповсюджена річ у цьому світі, оскільки кожен думає, що він наділений ним повною мірою.

Неможливо вигадати чогось оригінального і малоймовірного, що не було б уже сказано кимось із філософів.

ІV. Підведення підсумків. Вікторина.

1. Національність Рене Декарта? (француз)
2. Дата народження Рене Декарта? (31 березня 1596 рік)
3. Галузь наукови інтересів? (матеатика, фізика, філософія)
4. Громадянство Рене Декарта? (Париж)
5. Латинізоване імя Декарта? (Картезій)
6. Яке було хоббі у Рене Декарта? (Подорожування)
7. Розділ фізики якому залишив великий внесок Декарт? (Оптика, Механіка)
8. Як звали королеву, яка запросила Рене давати їй приватні уроки з філософії? (Христина)
9.  Доля якої відомої людини вплинула на публікацію праць Декарта в астрономії? (Галілей)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Математичний QR-квест (зашифровані «крилаті» вислови відомих математиків про математику

 

 

 

 

 

 

 

 

 

 

Вікторина : «Цікаві історії з життя видатних математиків»

1. Прізвище якого вченого нагадує «ланцюжок бінома?» (Ньютона)
2. Який учений брав у свою школу тільки тих, хто міг до вступу зберігати мовчання протягом п’яти років? (Піфагор)
3. Який математик, почувши відповідь від батька на запитання, що геометрія - це спосіб креслити правильні фігури і знаходити відношення, що існують між ними, почав нею займатися і став видатним? (Блез Паскаль)
4. Якого математика мають на увазі, коли говорять, що лічити він почав раніше, ніж навчився розмовляти? (Карл Гаус)
5. Який учений в дитинстві носив у кишені мотузку з прив’язаним до неї камінчиком, з допомогою якого вимірював глибину криниць, що траплялися йому? (М.В.Остроградський)
6. Про якого вченого сказано: «Те, що він зробив у геометрії, фахівці порівнюють з революційним переворотом Коперніка в астрономії» (М.І.Лобачевський).
7. Цар запитав математика, чи не має в геометрії коротшого шляху, ніж той, що його пропонує він. На це вчений відповів: «Ні, в математиці навіть для царів немає інших шляхів!..» Хто він? (Евклід)

 

 

 

 

 

Ребуси

                                    4=Р

 

                     1=К

 

 

 

                                      4=Т

 

 

 

 

 

Використана література

 

1.     Видатні наукові відкриття / Авт.-упорядники В. М. Скляренко, Т. В. Іовлєва, О. Ю. Очкурова. Х.: Фоліо, 2008. (Дитяча енциклопедія).

3.     Все для вчителя. Рубрика «Колумби математики» (№1, 2007).

4.     Все для вчителя. Рубрика «Трибуна вчителя» (№1-2, 2009).

5.     Математика (Всеукраїнська газета). (№7, №30, 2008).

6.     Конфорович А. Г. Видатні математичні задачі. К.: Рад. Школа, 1981.

7.     Конфорович А. Г. Математика служить людині. К.: Рад. Школа. 1984.

8. Архімед [Електронний ресурс]. - Електрон. дані. - Режим доступу: http://uk.wikipedia.org/wiki/Архімед. - Загол. з титул. екрану. - Мова: укр., рос., англ. та ін. - Перевірено: 20.01.2009.

9. Гаус Карл Фрідріх [Електронний ресурс]. - Електрон. дані. - Режим доступу: http://uk.wikipedia.org/wiki/Гаус_Карл_Фрідріх. - Загол. з титул. екрану. - Мова: укр., рос., англ. та ін. - Перевірено: 20.01.2009.