Посібник з теми "Розв’язування задач з параметрами графічним методом"

«Розв’язування задач з параметрами графічним методом»

Метою цього посібника є формування в читачів мислення розгалудженя, елементарних навичок роботи з параметрами, розвиток графічної культури, творчого мислення.

Посібник може бути використаний на уроках математики (особливо в профільних класах), на факультативах, при підготовці учнів до ДПА та ЗНО.

Специфіка задач із параметрами полягає в тому, що вони охоплюють усі теми алгебри, тому є унікальним засобом для систематизації й узагальнення навчальних досягнень учнів. Високий рівень абстрагування та алгоритмізації, що містять задачі з параметрами, розвиває навички застосування евристичних, дослідницьких прийомів роботи, вміння встановлювати причинно-наслідкові зв’язки, культуру мислення, ініціативу, творчість, а також забезпечити інтелектуальний розвиток особистості.

Цей збірник допоможе вчителям формувати в учнів міцні навички розв’язування задач з параметрами різної складності. Опрацьовуючи матеріал посібника, учні зможуть ліквідувати прогалини в знаннях і вміннях, розширити та поглибити знання, підвищити рівень власної підготовки.  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Зміст

1. Знайомство з параметром.
2. Що потрібно знати і чим користуватись.
   1. Прямі і кола.
   2. Модуль.
   3. Квадратична функція і не тільки.
3. Приклади розв’язування задач.

3.1. Рівняння.

3.2. Системи рівнянь

3.3. Нерівності.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1. Знайомство з параметрами

В основу розв’язання задач із параметрами покладено такий принцип: значення параметра (або параметрів) вважається довільно фіксованим і розв’язок задачі знаходитися традиційними методами. Проте наявність параметрів у задачі передбачає обов’язкове дослідження існування розв’язку залежно від конкретних числових значень параметрів із області їх допустимих значень, а також знаходження всіх таких розв’язків. Задачі з параметрами, таким чином, розглядаються як ціла множина рівнянь, нерівностей або їх систем, які отримуються, коли параметри набувають конкретних значень. Форма запису відповіді у задачах з параметрами має спеціальний вигляд: значення невідомих вказуються для кожного допустимого значення параметрів.

    Для розв’язання задач з параметрами необхідні ґрунтовні знання властивостей елементарних функцій, рівносильних перетворень рівнянь та нерівностей.

Задача з параметрами крім букв, що позначають невідомі, містять інші букви, які називаються параметрами. Фактично ми маємо справу не з одним завданням, а з їх нескінченною множиною.

    Розв’язати завдання з параметром означає, що потрібно навести у відповіді сімейство розв’язків відносно невідомої величини для всіх можливих сталих величин (параметрів).

Важливо! Параметр у відповіді повинен «пробігти» всю числову вісь, або всі значення , що обумовлені умовою задачі.

Так, з параметрами учні зустрічаються при введенні деяких понять. Розглянемо як приклади наступні об’єкти.

Функція пряма пропорційність: y=kx  (x і y  - змінні, k – параметр,  );

Лінійна функція: y=kx+b (x і y  - змінні, k i b – параметри);

Лінійне рівняння: ax+b=0 (x - зміннa, a i b – параметри);

Рівняння першого степеня: ax+b=0 (x - зміннa, a i b – параметри, );

Квадратне рівняння: (x - зміннa, a, b і с – параметри, ).

До задач з параметрами, можна віднести, наприклад, пошук розв’язків лінійних і квадратних рівнянь в загальному вигляді, дослідження кількості їх коренів в залежності від значення коефіцієнтів.

 Основне, що потрібно засвоїти при першому знайомстві з параметром, - це необхідність обережного звертання до фіксованого але невідомого числа.

Існує три загальноприйняті методи розв’язання задачі з параметром: аналітичний, графічний та відносно параметра.

Аналітичний  -  універсальний, але найбільш складний, і потребує високої математичної грамотності.

Графічний – виключно красивий і наочний але не завжди доречний і потребує мистецтва роботи з графіками.

В цьому посібнику ми звернемо увагу саме на графічний спосіб.

Суть методу полягає в тому, що задачу зводять до з’ясування взаємного розташування графіків рівнянь що містять параметри по відношенню до графіків рівнянь які  у своєму складі не містять параметрів.

Найчастіше графічно розв’язують ті задачі, де потрібно знайти кількість розв’язків, коли в задачі є «впізнавана функція», в задачах з модулями.

До того ж в  деяких випадках аналітичний метод розв’язування «тягне за собою» таку кількість систем і сукупностей, що в них дуже легко заплутатись. І тоді на допомогу приходить графіка.

 

2. Що потрібно знати і чим користуватись.
   1.                   Щоб розв’язувати графічно задачі з параметрами необхідно вміти будувати і перетворювати графіки функцій та залежностей. В цьому розділі – відомості про графіки функцій і залежностей, які найчастіше зустрічаються.

1. Пряма    y=kx+b

k – змінна b - const	пряма «обертається» навколо точки (0; b) (рівняння прямої з полюсом)
b – змінна k  - const	y=kx   рухається вздовж осей координат
y=k1 x+b1 y=k2 x+b2	k1 = k2	прямі паралельні
	k1 k2 = - 1	прямі перпендикулярні

2. Коло   (x-a)² + (y-b)²=R²

a – змінна b – const R - const	коло «рухається» вздовж осі Ох
b – змінна a  - const R - const	коло «рухається» вздовж осі Оу
a – const b – const R - змінна	«сім’я» концентричних кіл з центром в точці (а; b)

Коло і пряма: перетинаються (2 спільні точки), дотикаються (1 спільна точка), не перетинаються (не мають спільних точок).

2.2. Модуль.

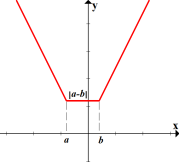
Графік функції виду  у = |х - а| + |х - b|

«дно»:  у = |а - b|

 

 

 

 

Графік залежності виду  |х| + |у|= т – квадрат

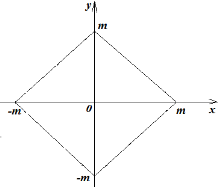|х - а| + |х - b|= т

a – змінна b – const т - const	квадрат «рухається» вздовж осі Ох
b – змінна a  - const т - const	квадрат «рухається» вздовж осі Оу
a – const b – const т - змінна	«сім’я» концентричних квадратів з центром в точці (а; b)

3.              Квадратична функція.

Про графік квадратичної функції написано багато. На мою думку цей конспект (посібник Г.В.Апостолова, В.В.Ясінський «Перші зустрічі з параметром»)– найкраще узагальнення відомостей про графік квадратичної функції.

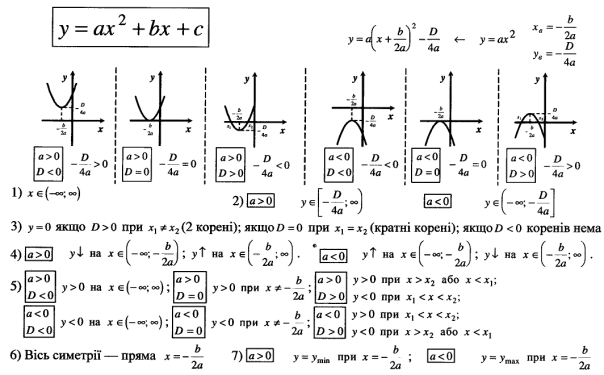Але розділ називається «Квадратична функція і не тільки». Тож давайте дослідимо ще деякі випадки непрямого використання квадратичної функції на прикладах.

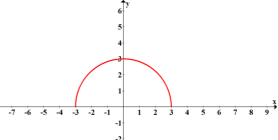
Графік функції – півколо з центром в (0;0),  радіусом 3  (y ≥ 0)

 

 

 

 

 

 

 

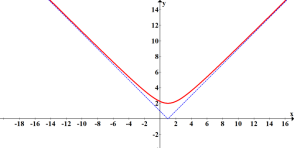
ОВ:

- асимптоти

 

 

 

 

 

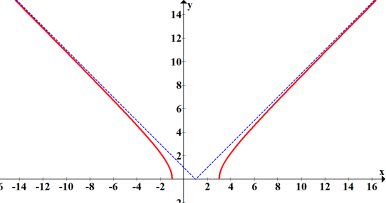
ОВ:

 

- асимптоти

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3. Приклади розв’язування задач.
   1.          Рівняння

1. Знайдіть всі значення параметра а при якому рівняння має менше 4 коренів

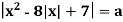
Розв’язання

Запишемо рівняння в виді: 

Нехай  f(x) =          g(x)=

 

 

 

 

 

 

 

 

 

 

 

 

 

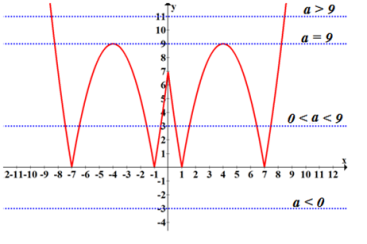
Схематично зобразимо  графіки функцій f(x) та g(x)

Графік функції   g(x)=  - пряма, паралельна осі Ох. Розв’язки рівняння – абсциси точок перетину графіків функцій. Пряма не перетне графік f(x), якщо а < 0 і якщо а >9, то пряма матиме з графіком менше чотирьох точок перетину (а саме дві). Тобто, рівняння має менше 4 коренів коли

Відповідь: 

 

2. Знайти всі значення параметра а при яких найменше значення функції  f(x) дорівнює найбільшому значенню функції     g(x).

f(x)=|x - 1|+|x - 3|+a

g(x)=

Розв’язання

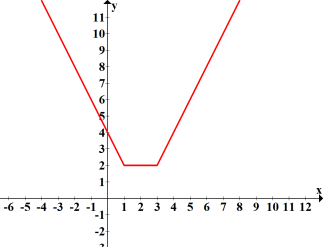Графік  функції  g(x)- парабола, вітки вниз, найбільшого значення досягає в вершині: х = 0;  g(x)=

f(x)=|x - 1|+|x - 3|+a

Побудуємо графік

 у =|x - 1|+|x - 3|. 

 

 

 

Найменше значення у = 2+a

Значить

 

Відповідь:  

 

 

 

3.            Розв’яжіть рівняння для всіх дійсних значень параметра а.

|x² - 4|-|x² - 9| =

Розв’язання

Розглянемо дві функції  f(x)= |x² - 4|-|x² - 9| і g(x)=.

Схематично зобразимо графік f(x).

Для цього знайдемо нулі модулів і знаки модулів на проміжках

Для х ≤ -3 або х ≥ 3,                f(x)=5

Для -3< x < -2  і 2< x < 3,       f(x)=2х²- 13

Для -2< x < 2   f(x)= - 5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

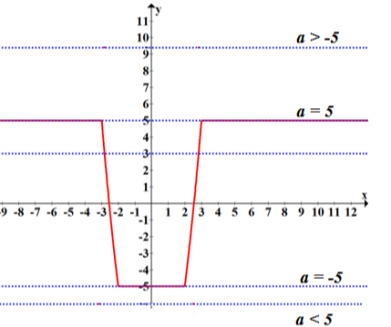
Відповідь:  якщо < -5 або >5,  то рівняння розв’язків не має

якщо = -5, то

якщо = 5, то

якщо то

 

 

4. Розв’яжіть рівняння для всіх дійсних значень параметра а

Розв’язання

Розглянемо дві функції  f(x)= і   g(x)=

Побудуємо графік  f(x).  Це півколо радіусом   для  f(x) ≥ 0

Графік  g(x)= – пряма

 

 

 

 

 

 

 

 

 

 

 

 

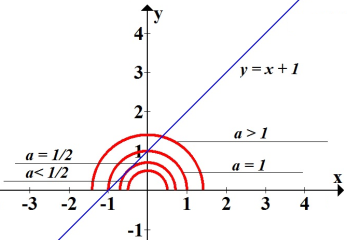
1. Пряма дотикається до півкола:

З прямокутного трикутника  ОАВ (рис.1)

, тобто    

 

 

 

 

 

 

 

 

 

 

 

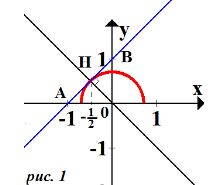
2. Пряма не перетинає півколо коли  
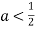
3.                     Пряма перетинає півколо в 2-х точках (розв’язках рівняння 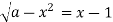), якщо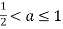

тобто:

4.                     Пряма перетинає півколо в одній точці:

це більший з двох розв’язків даного  рівняння  - 

 

Відповідь:  якщо

якщо

якщо

якщо

5. ЗНО 2013. Знайдіть найменше ціле а при яких рівняння має рівно 2 розв’язки.

Розв’язання

Виконаємо перетворення і перепишемо рівняння у вигляді:

ОДЗ: 

x=5 – розв’язок

значить задача зводиться до того , щоб знайти а, при якому рівняння має один розв’язок, який ≠ 5

функція монотонно зростає на всій ОДЗ, тобто має найменше значення в  х=5.

 

Підставимо х=5 в рівняння:

 

 

 

 

 

 

 

 

 

 

 

 

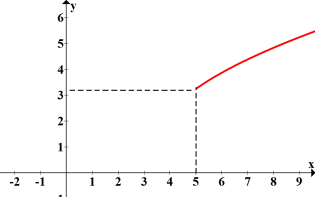
За умовою задачі а – ціле, значить

Найменше з таких значень

Відповідь:.

 

6. Розв’яжіть рівняння для всіх дійсних значень параметра а

Розв’язання

Розглянемо дві функції  f(x)= і   g(x)=

Побудуємо графік функції  f(x)= за допомогою геометричних перетворень

Графік g(x)= - горизонтальна пряма, що рухається вгору-вниз по осі Оу

 

 

 

 

 

 

 

 

 

 

 

 

 

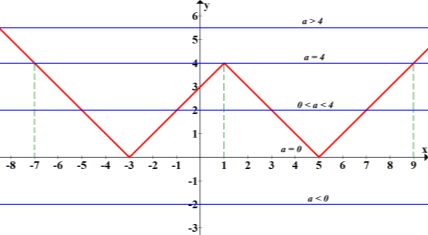
От і все, можемо писати відповідь.

Відповідь: якщо

якщо

якщо

якщо

якщо

 

2.                   Системи рівнянь

 

1. Скільки розв’язків має система в залежності від параметра а?

Розв’язання

Виконаємо перетворення і запишемо систему в виді:

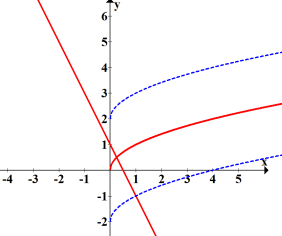
Побудуємо графік першого рівняння і схематично зобразимо графік другого.

це графік  , який рухається вгору-вниз по осі Ох. Очевидно, що при  - графіки перетинаються в одній точці, а при – графіки не перетинатимуться.

 

 

 

 

Відповідь: якщо - система має 1 розв’язок

якщо - система розв’язків не має

 

 

 

2. ЗНО 2014.  Знайдіть усі від’ємні значення параметра а при яких система рівнянь має єдиний розв’язок. Якщо таке значення одне, то запишіть його у відповідь. Якщо їх кілька – то у відповідь запишіть їхню суму.

 

 

Розв’язання

Після очевидних перетворень система набере вигляду:

       →       →         

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

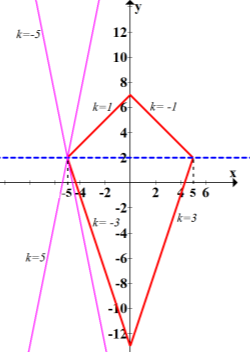
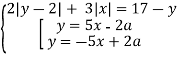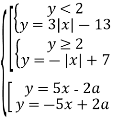
Рівняння запишемо в виді

Графічним зображенням  цієї сукупності є ромбоїд

 

Графічним зображенням сукупності     є «сім’я прямих» з кутовим коефіцієнтом 5 і -5.

Оскільки а<0 , то прямі проходять через точку (-5;2). Отже,

      або     

Відповідь: -25

 

3)  Знайдіть всі значення параметра при якому система має безліч розв’язків

Розв’язання

Побудуємо графіки обох рівнянь в одній системі координат.

Графік першого рівняння – дві паралельні прямі: y = x + 2 і  y = x – 2

Графік другого рівняння – кут, що рухається вгору-вниз по вісі Оу.

Кутові коефіцієнти прямих і правої сторони кута однакові і  дорівнюють 1.

 

 

 

 

 

 

 

 

 

 

 

 

 

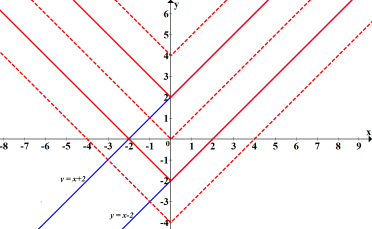
Очевидно, що система має безліч розв’язків при а = ±2

Відповідь: -2; 2.

 

4) Знайдіть всі значення параметра при якому система має один  розв’язок

Розв’язання

Побудуємо графіки обох рівнянь в одній системі координат.

Графік першого рівняння – дві паралельні прямі: y = -x + 2 і  y = -x – 2

Графік другого рівняння – кут, що рухається вгору-вниз по вісі Оу.

Кутові коефіцієнти прямих і лівої сторони кута однакові і  дорівнюють -1.

 

 

 

 

 

 

 

 

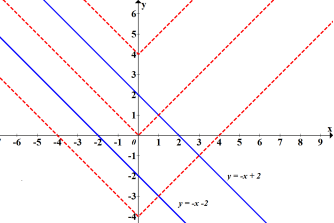
Очевидно, що система має один розв’язок  при  -2 < а < 2

 Відповідь:

 

5) Знайдіть всі значення параметра при якому система має рівно два  розв’язки

Розв’язання

Побудуємо графіки обох рівнянь в одній системі координат.

Для побудови графіка першого рівняння розкриваємо модуль.

  Графік другого рівняння – квадрат, що рухається вздовж Ох.

Якщо а ≥ 1, то система завжди має 2 розв’язки.

Ще один випадок двох розв’язків матимемо, при а = -2

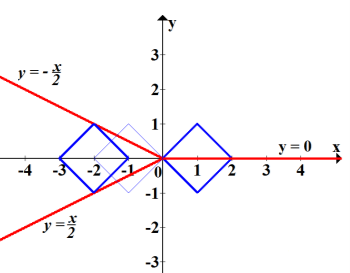В інших випадках система не має розв’язків, або їх кількість не дорівнює двом.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Відповідь:

 

6) Знайдіть всі значення параметра при якому система має один  розв’язок

 

 

Розв’язання

Перепишемо дану систему в виді:

 

Побудуємо графіки обох рівнянь в одній системі координат.

Аналогічно попередньому завданню для побудови графіка першого рівняння розбиваємо  нулями модулів координатну площину на частини, шукаємо знаки модулів в кожній частині і, розкриваючи модуль, будуємо графіки в кожній частині координатної площини. Щоб знайти знаки модулів в кожній частині площині підставляємо будь-яку точку з цієї частини в кожний модуль.

Нулі модулів:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

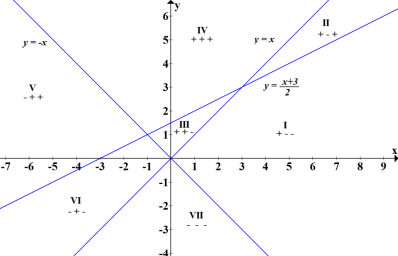
Будуємо графік рівняння:

І.

      - графіку належить частина прямої

ІІ.  

      - графіку  належить 1 точка – (3; 3)

IIІ.  

    - графіку належать всі точки частини ІІІ

IV.      

      - графіку належить частина прямої

V.  

       -  графіку  належить 1 точка – (-1; 1)

VI.         

       - графіку належить частина прямої

VII.         

       -  графіку  належить 1 точка – (0; 0)

Тобто графік першого рівняння – трикутник (частина ІІІ) разом з його внутрішньою областю.

Графік другого рівняння – сім’я концентричних кіл з центром в т.(0;-1)

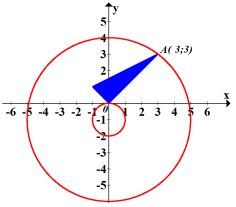Система має один розв’язок коли трикутник і коло дотикаються.

Це можливо в т.(0;0) і в т.(3;3). Підставляючи координати точок в друге рівняння, одержуємо:

 ,    або

 

 

 

Відповідь: -5, -1, 1, 5.

 

 

3.3. Нерівності.

1. Розв’яжіть нерівність для всіх дійсних значень параметра а.

|x - 2|+|x + 3|≤ a

Розв’язання

Побудуємо графіки функцій  у=|x - 2|+|x + 3| і  у=а

При a<5 графіки не перетинаються, і ніяка частина у=|x - 2|+|x + 3|  не лежить нижче прямої, тож нерівність розв’язків не має

При a=5 графіки мають спільний відрізок який і є розв’язком

При a >5 графіки  перетинаються в двох точках, частина графіка у=|x - 2|+|x + 3|   лежить нижче прямої у = а

Знайдемо точки перетину у=|x - 2|+|x + 3| і у=а

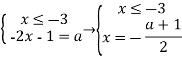
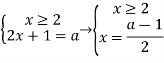
При а>5 графіки перетинаються в точках х₁= і х₂=

 

 

 

 

 

 

 

 

 

 

 

 

 

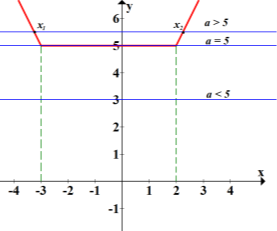
Відповідь: якщо a<5                

якщо = 5,            

якщо

 

2. Розв’яжіть нерівність для всіх дійсних значень параметра а.

Розв’язання

Розглянемо дві функції  f(x)= і   g(x)=

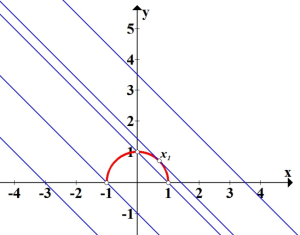
Графік f(x)= - півколо в додатній площині з радіусом 1;

графік  g(x)= – пряма: k =-1 , що рухається вздовж осей координат. Розв’язками нерівності будуть абсциси тих точок півкола, які лежать нижче прямої.

Побудуємо графіки функцій. 

Очевидно, що при  a≤-1 пряма не перетинає півколо, значить нерівність розв’язків не має.

Якщо , то пряма перетинає півколо в одній точці, тож розв’язком нерівності буде один інтервал.

Якщо то пряма перетинає півколо в двох точках, розв’язок нерівності – 2 інтервали.

Знайдемо координати точок перетину прямої з півколом. Для цього розв’яжемо рівняння:

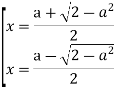
Пряма приймає положення дотичної коли →

 

 

 

 

 

 

 

 

 

 

 

 

 

Відповідь: якщо

якщо

якщо

якщо

якщо

 

3. Знайдіть усі значення параметра а при яких система  має єдиний розв’язок.

 

 

Розв’язання

Перепишемо систему в виді:

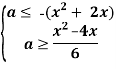
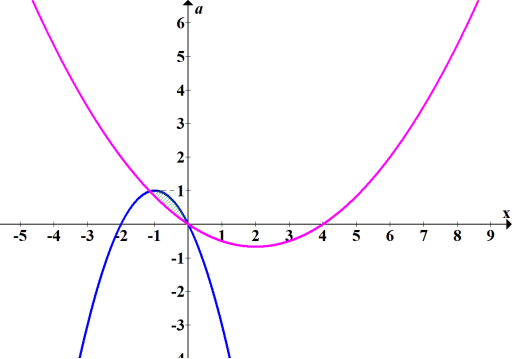Розглянемо систему координат Xoa. Побудуємо в цій системі графіки функцій та

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розв’язком системи нерівностей є заштрихована частина графіку.

Система матиме один розв’язок лише при а = 0 та а = -1.

Відповідь: 0; 1.

 

 

 

4. Знайдіть усі значення параметра а при яких множина розв’язків системи є відрізок вказаної довжини. (l = 1)

 

 

Розв’язання

Перепишемо систему в виді:

   →        

 

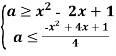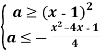
Розглянемо систему координат Xoa. Побудуємо в цій системі графіки функцій

    та 

 

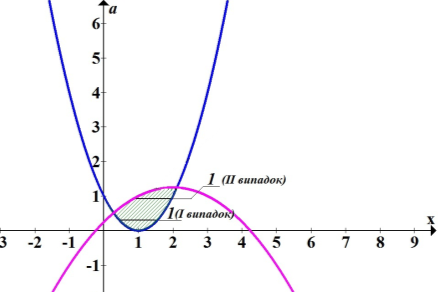
Може бути два випадки, коли розв’язком системи є відрізок довжиною 1. Знайдемо при якому значенню параметра це відбувається.

І випадок. Знайдемо корені рівняння:

 

Шуканий випадок буде при умові:

ІІ випадок. Знайдемо корені рівняння:

Виберемо менший корінь:
 

Шуканий випадок буде при умові:

Відповідь: 1, .

 

 

5) Розв’яжіть нерівність для всіх дійсних значень параметра а.

 

Розв’язання

Розглянемо дві функції та .

Побудуємо їх графіки в одній системі координат.

Розглянемо такі випадки:

І. Якщо то

ІІ. Якщо то графік має вигляд:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

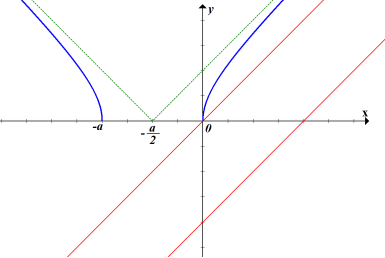
Пряма () завжди буде проходити нижче графіка . Тож розв’язками нерівності буде область визначення функції . Тобто

якщо

ІІІ. Якщо то графік має такий вигляд:

 

 

 

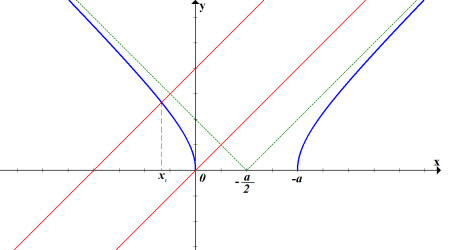
Так як кутові коефіцієнти прямої і асимптоти однакові, пряма буде перетинати графік в одній точці . Знайдемо х₁.

 

Тобто, якщо

якщо

Відповідь: якщо то

якщо ;

якщо

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Використана література:

 

1. Г.В.Апостолова, В.В.Ясінський Перші зустрічі з параметром. - К.: Факт, 2006. – 324с.
2. В.В. Ясінський Математика. Навчальний посібник для слухачів ІДП НТУУ «КПІ».-К.: ІДП НТУУ «КПІ», 2014. – 472с.
3. Є.П.Нелін Алгебра і початки аналізу. Підручник для 10 класу загальноосвітніх навчальних закладів. Профільний рівень. – Х. : Гімназія, 2010. – 416с.