Повторення. Числові та лінійні нерівності.

Тема уроку. Повторення. Числові та лінійні нерівності.

Тестові завдання

1. Яку подвійну нерівність задовольняє множина чисел, поданих на рисунку?

а) -4 < x < 8;  б) -4 < х < 8;  в) -4 < х < 8;  г) -4 < х < 8.

2. Відомо, що х < у. Яка з наведених нерівностей є правильною?

а) 3х < 3у;  б) x – 3 < y – 3; в) -3х > -3у;  г) х + 3 > у + 3.

3. Який із проміжків є розв'язком нерівності 3х + 2 > х – 8?

а) (-∞; -5);   б) (-∞; -5];   в) (-5; +∞);   г) [-5; -∞).

4. Яка з нерівностей є правильною?

а) ;  б) ;   в) ;  г) 0,(3) > .

5. Оцініть довжину сторони квадрата а см, знаючи, що його пе­риметр дорівнює Р см і 0,24 < Р < 0,36.

а) 0,4 < а < 0,6; б) 0,6 < а < 0,9; в) 0,12 < а < 0,18;  г) 0,24 < а < 0,6.

6. Відомо, що т > 0 і п > 0. Порівняйте з нулем вираз т⁵п⁶.

а) т⁵п⁶ < 0;   б) т⁵п⁶ > 0;   в) т⁵п⁶ ≤ 0;   г) т⁵п⁶ ≥ 0.

7. Знайдіть середнє арифметичне всіх цілих чисел з проміж­ку (-4; 5].

а) ;   б) 1;   в) -4,5;  г) -1.

8. Яке з наведених тверджень є неправильним?

а) Якщо почленно додати правильні нерівності одного знака, залишивши їх спільний знак, то дістанемо правильну чис­лову нерівність.

б) Якщо з однієї частини нерівності перенести в іншу доданок з протилежним знаком, то дістанемо нерівність, рівносиль­ну даній.

в) Число т більше від числа п, якщо т – п — додатне число.

г) Якщо обидві частини нерівності помножити або поділити на будь-яке число, то знак нерівності не зміниться.

Задачі

1. При яких значеннях b різниця дробів 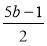і 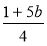додатна?
2. Оцініть значення виразу 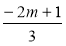, якщо 2 ≤ m ≤ 3.
3. При яких значеннях х визначена функція ?
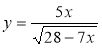4. Розв'яжіть нерівність (х – 1)² – (х + 2)(х – 3) ≤ 2х – 1 та запишіть відповідь у вигляді числового проміжку.
5. Доведіть, що вираз (х + 2)(х² – 2х + 4) – (х² – 2)(х + 1) набуває додатних значень при всіх дійсних значеннях х. Якого наймен­шого значення набуває цей вираз і при якому значенні х?
6. Розв'яжіть нерівність 4 – |x + 9| > 3(|x + 9| – 4).