Повторення, систематизація і узагальнення матеріалу, вивченого у сьомому класі

Тема. Повторення, систематизація і узагальнення матеріалу, вивченого у сьомому класі

Мета: повторити, систематизувати і узагальнити знання учнів, набуті ними в ході вивчення геометрії в сьомому класі. Повторити і систематизувати дії учнів при розв'язуванні задач, під час якого учні самостійно працюють із довід­ковим матеріалом і класифікують задачі, послідовно складаючи загальні алгоритми розв'язання задач вио­кремлених типів.

Тип уроків: повторення, узагальнення і систематизація знань і вмінь учнів, набутих ними підчас вивчення геометрії в сьомому класі.

Обладнання: набір демонстраційного креслярського приладдя, уза­гальнені таблиці: «Кути. Відрізки», «Трикутники», «Коло. Геометричні побудови».

Хід уроку

Методичний   коментар

Згідно з чинною програмою з математики наприкінці на­вчального року відведено шість годин для повторення і систе­матизації вивченого протягом року навчального матеріалу. Зрозуміло, що найкращим способом для цього є розв'язання задач за тематикою, що відповідає програмі, а саме — з трьох основних тем:

• відрізки і кути;
• трикутники;
• коло і геометричні побудови.

Форма проведення уроків повторення і систематизації ма­теріалу може варіюватись: від стандартних уроків повторення, узагальнення і систематизації знань і вмінь (див. вище), що передбачають самостійну роботу учнів з довідковим матеріалом і складання узагальнених схем, таблиць, алгоритмів тощо, з по­дальшим використанням складених схем, таблиць і алгоритмів при розв'язуванні задач, до нестандартних уроків: уроків-вікторин, уроків брейн-рингів тощо. Форми і методи організації роботи учнів на цих уроках кожен учитель обирає самостійно на свій розсуд, залежно від рівня підготовки учнів і ступеня їхньої організованості.

Створенню відповідної робочої атмосфери на уроках спри­ятиме не тільки вдало обрана форма проведення уроків, але й відповідним чином підібрані задачі. Запропонована нижче підбірка задач (на думку автора) сприятиме підвищенню рівня пізнавальної активності учнів на цих уроках.

Усні   вправи

1. Як перевірити правильність виготовлення лінійки?
2. Чи правильні такі твердження:

а) через точку площини можна провести не менш, як 1000 прямих;

б) сполучивши парами три точки площини, завжди діста­немо три прямих;

в) на  кожній  прямій  можна  вибрати  принаймні   1000 точок?

3. Яким є взаємне розміщення двох різних прямих на площині, якщо вони мають: а) принаймні одну спільну точку; б) не більш як одну спільну точку?
4. Чи є правильним твердження: «Через дві різні точки за­вжди можна провести промінь, причому тільки один»?
5. Чи можна на відрізку завдовжки 1 см розмістити 1 000 000 точок?
6. Щоб зняти копію з рисунка, утвореного лише з відріз­ків, підкладають під рисунок чистий аркуш паперу і проколюють тоненькою голкою кінці всіх відрізків. Сполучивши відповідним чином утворені на чистому папері проколи, дістають потрібну копію. Обґрунтуйте правильність цих дій.
7. Як можна наближено знайти товщину однієї сторінки посібника з геометрії?
8. Два учні накреслили кути по 45°, і один із них сказав: «У мене кут більший, оскільки в нього сторони довші». Чи так це?
9. Чи є правильним твердження: «Для кожного кута завж­ди можна побудувати тільки один вертикальний кут і тільки один суміжний кут»? Відповідь поясніть.
10. Чи є правильним твердження: «Якщо один із суміжних кутів зменшити у два рази, то другий кут збільшиться у два рази»?
11. Проти кожної поділки транспортира записано два числа, сума яких дорівнює  180°. Чим це пояснюється?
12. Який найбільший кут можна утворити вказівним і се­реднім пальцями лівої руки? Як виміряти цей кут за допомогою транспортира?
13. Який кут — гострий, тупий чи розгорнутий — утворюють стрілки годинника, коли вони показують 3 год, 7 год, 10 год?
14. На дошці було зображено кут і його бісектрису. Хтось витер частину рисунка — одну із сторін кута. Як можна відновити рисунок? Скільки розв'язків має задача?
15. Відрізки МС і АВ перетинаються в точці О, причому АО = СО. Які відомості ще потрібні, щоб можна було стверджувати, що  AM = СВ ?
16. Чи можна, за аналогією до ознак паралельності прямих, сформулювати ознаки непаралельності прямих?
17. Як за допомогою транспортира переконатися, що дві прямі не є паралельними?
18. Чому на прямолінійних ділянках залізниці рейки мають бути паралельними?
19. У рівнобедреному трикутнику один із кутів при основі дорівнює 45°. Чи можна стверджувати, що цей трикут­ник прямокутний?
20. Чому не існує тупокутних рівносторонніх трикутників; прямокутних рівносторонніх трикутників?
21. Доведіть, що твердження: «У рівнобедреному трикутнику кут при основі  96°» не може бути слушним.
22. Якої величини має бути кут при основі рівнобедреного трикутника, щоб трикутник був гострокутним; прямо­кутним; тупокутним?
23. Скільки кутів трикутника мають бути відомими, щоб можна було визначити решту кутів цього трикутника? Розгляньте випадки: а) довільний трикутник; б) прямо­кутний трикутник; в) рівнобедрений трикутник; г) рівносторонній трикутник; д) прямокутний рівнобедрений трикутник.
24. Чи можна в трикутнику ABC провести відрізок AM так, щоб утворилися два гострокутні трикутники?
25. Яким — гострокутним, прямокутним чи тупокутним — є трикутник, у якого:

один із кутів дорівнює сумі двох інших;

один із кутів більший за суму двох інших;

один із кутів менший від суми двох інших.

26. Чи є правильним твердження: «Існує трикутник з най­більшим кутом 56°»?
27. Чи є правильним твердження: «Існує трикутник з най­меншим кутом  65°»?
28. Учень сказав: «Прикладами хорд є діаметри і радіуси». Чи правильно це?
29. На колі взято точку. Скільки діаметрів і скільки хорд можна провести через цю точку?
30. Спростуйте твердження: «Пряма, перпендикулярна до радіуса кола, дотикається до цього кола».
31. У трикутнику ABC центр описаного кола лежить на медіані AM. Що можна сказати про цей трикутник?
32. На дошці зображено відрізок АВ.
33. Як побудувати рівносторонній трикутник ABC? Подайте план побудови. Скільки розв'язків має задача? Як побудувати рівнобедрений прямокутний трикутник ABC з прямим кутом В? Подайте план побудови.  Скільки розв'язків має задача?
34. Дано пряму а і точку В, яка не лежить на цій прямій. Як на прямій а знайти точки, віддалені від В на 10 см? Подайте план розв'язування. Чи завжди існують такі точки? Скільки їх може бути?
35. Учень накреслив на дошці коло радіуса 20 см, але забув позначити центр. Як знайти центр кола? Подайте план розв'язання.
36. Як за допомогою циркуля й лінійки побудувати кут, який дорівнює  45°, 30°?

Письмові   вправи

1. На прямій позначено послідовно точки А, В і С. Чи прав­да, що відстань між серединами відрізків АВ і ВС вдвічі менша від відрізка АС?
2. Знаючи, що АВ = 7, знайдіть на прямій АВ таку точку М, щоб АМ – ВМ = = 1.
3. Різниця двох суміжних кутів дорівнює одному з цих кутів. Знайдіть кожний з цих кутів.
4. Один із суміжних кутів удвічі більший за різницю між ними. Знайдіть ці кути.
5. Два рівних кути мають спільну вершину, їх бісектри­си — доповняльні промені. Доведіть, що ці кути — вер­тикальні.
6. Медіана AM трикутника ABC продовжена до точки Е так, що ME = AM. Якій із сторін трикутника ABC дорівнює відрізок СЕ?
7. Доведіть, що висоти трикутника, перетинаючись, не ді­ляться навпіл.
8. На сторонах кута А взято точки В і С так, що АВ = АС. Перпендикуляри до сторін кута в цих точках перети­наються в точці О. Чи лежить точка О на бісектрисі кута А?
9. Трикутник ABC — рівнобедрений, його основу АВ про­довжили в обидва боки так, що 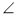ACE = 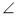BCM. Доведіть, що  АЕ = ВМ.
10. Трикутники ABC і АВМ рівні. Доведіть, що їх спільна сторона перпендикулярна прямій СМ.
11. Доведіть, що гострокутні трикутники рівні, якщо ос­нова і висоти, проведені до бічних сторін одного три­кутника, рівні основі і відповідним висотам іншого трикутника.
12. Доведіть, що трикутник, у якого дві висоти рівні, є рівнобедреним.
13. Попарні суми сторін трикутника дорівнюють 17 см, 18 см, 21 см. Знайдіть периметр трикутника.
14. Периметр трикутника більше його сторін на 32 см, 29 см і 23 см відповідно. Визначте периметр трикутника.
15. При перетині двох паралельних прямих січною утвори­лися вісім кутів, кожний з яких менше розгорнутого. Сума трьох із цих кутів дорівнює 207° . Знайдіть вели­чини кожного з восьми кутів.
16. AM — бісектриса кута А трикутника ABC, ME || AC . Доведіть, що ∆АМЕ   — рівнобедрений.
17. Сторони двох кутів відповідно паралельні. Чи рівні гра­дусні міри цих кутів?
18. Бісектриси внутрішніх кутів трикутника ABC перетина­ються в точці О. Доведіть, що кути АОВ, АОС, ВОС — тупі.
19. Визначте суму зовнішніх кутів трикутника (взятих по одному при кожній вершині). Чи може зовнішній кут трикутника дорівнювати сумі двох інших зовнішніх кутів?
20. Внутрішні кути трикутника відносяться як 1:4:7. Як відносяться зовнішні кути цього трикутника?
21. Один із кутів трикутника дорівнює сумі двох інших, а другий кут трикутника дорівнює третині від суми ін­ших. Знайдіть кути трикутника.
22. Бісектриса кута при вершині трикутника перетинає основу під кутом 73°, а бісектрису одного з кутів при основі — під кутом  58°. Знайдіть кути трикутника.
23. Чи може бісектриса кута трикутника розділити три­кутник на два рівнобедрених трикутники? Якщо так, визначте кути даного трикутника.
24. З вершини найбільшого кута прямокутного трикутни­ка проведено бісектрису і висоту, кут між якими 17°. Знайдіть гострі кути трикутника.
25. У прямокутному трикутнику катет довжиною 12 см ле­жить при куті 30° . Знайдіть довжину бісектриси іншого гострого кута.
26. *Гіпотенуза прямокутного трикутника у чотири рази більше висоти, що проведена до неї. Знайдіть гострі кути трикутника.
27. *Три кола, радіуси яких 2 см, 3 см, 9 см, парами до­тикаються. Визначте периметр трикутника з вершинами в центрах цих кіл.
28. Дано коло і точка М поза ним. Як провести через точ­ку М пряму, яка перетинатиме коло в точках, відстань між якими дорівнює а?
29. Побудуйте коло, яке проходить через дану точку А і до­тикається прямої l у даній точці В.
30. Дано коло і пряма l. Побудуйте коло, яке дотикатиметься прямої l і в даній точці дотикатиметься кола.
31. Кути трикутника відносяться як 3:7:8. Під якими ку­тами видно його сторони з центра вписаного кола?