Повторювально-узагальнюючий урок з теми: «Лінійна функція»

Тема: Повторювально-узагальнюючий урок

з теми: «Лінійна функція»

 Мета: узагальнити та систематизувати знання учнів про основні поняття теми;повторити набуті навички під час розв’язування теоретичних та практичних вправ;розвивати логічне мислення,пам'ять,вміння узагальнювати й аналізувати;виховувати вміння працювати в групі, розвивати творчість, ініціативу, зацікавленість предметом, комунікативні здібності учнів.

 Попередня підготовка до уроку. Клас розбивається на групи,діти повинні придумати назву команди,девіз та емблему,пов’язані з темою,що вивчили.  Заздалегідь учням повідомляється орієнтовний перелік теоретичних та історичних питань з теми.

 Урок починається  з вступу та ознайомлення учнів з правилами гри та конкурсами.

Правила гри:

• Кожна команда по черзі вибирає завдання на своєму полі. Час на міркування залежить від складності питання,час визначає ведучий(від 30 до 45с).
• У випадку правильної відповіді команда отримає від гномів кристал,  який дорівнює 1 балу.
• Якщо в полі завдання  є додатковий дорогоцінний кристал, то команда під час виграшу отримує 5 балів.
• В конці гри підводяться підсумки. Виграє команда, яка набрала більшу кількість балів.

 Перелік конкурсів:

1. Тест - „ хвилинка ”
2. Гра «Скарби гномів» (Додаток)
3. Конкурс капітанів
4. Фізкульхвилинка
5. Історична зупинка.
6. Бій команд.

Хід уроку

1.               Тест – „ хвилинка ”. Для визначення порядку участі у грі учням необхідно розгадати ребус.

Він є і у студента, і в учня.

                                              4,8,2,5,7,6,1  (Відповідь: Розклад)

2.               Гра «Скарби гномів».(Питання до гри розміщені в додатках). Учням двох команд пропонуються по черзі  питання. Оскільки клас був поділений на 4 групи,то учні 1 та 2 групи обирають питання для відповідей по черзі,використовується 5 питань.

  Після проведення першої частини гри проводиться конкурс капітанів, а члени чотирьох команд беруть участь  у  «Математичній фізкультхвилинці».

3.               Конкурс капітанів. В конвертах капітани отримують завдання,окремо від команд вони їх виконують. Кількість балів за виконане завдання розподіляється таким чином: учень,який першим виконав правильно завдання,   приносить в скарбницю команди  4 бали, другий − 3бали, третій − 2 бали, четвертий − 1бал.

Картка 1. Не виконуючи побудови, знайти координати точок перетину графіків в лінійних функціях y = x + 3 та  y = 4x − 6.(Відповідь: (3;6)).

Картка 2.  Не виконуючи побудову,визначити найменше значення лінійної функції y = 5x+2 на відрізку [−2;1]. (Відповідь: -8).

4. Фізкульхвилинка. Учням пропонується побудувати графік функції

у = - 0,5х + 2,  але побудова проводить у вигляді естафети.

Естафетною паличкою є олівець,якім діти виконують побудову.

1 учень. Заповнити таблицю залежності функції від аргументу

2 учень. Побудувати систему координат

3 учень. Нанести точки для побудови графіка.

4 учень. Провести графік функції.

 5 учень. Знайти координати точки перетину з віссю Ох.

6. учень. Знайти координати точки перетину з віссю Оу.

Продовження гри «Скарби гномів». Учням  наступних двох команд пропонуються по черзі ще 5 питань з гри «Скарби гномів».

5. Історична зупинка. Під час проведення цього конкурсу діти мають можливість отримати додаткові бали для команди, якщо підготували повідомлення про Р.Декарта, Г. Лейбница.

   Учням пропонується розгадати ребус та розповісти про Декарта.

 Вчитель: Про кого йдеться мова ?  Він – видатний німецький учений. За освітою –  юрист. Працював бібліотекарем,історіографом,організував Берлінську академію наук. Досліджував проблеми математики,філософії,конструював обчислювальні машини.( Відповідь: Г. Лейбниц).

6. Бій команд. На екрані спроектовані завдання, дітям пропонують виконати їх. Команда, яка робить це першою отримує 5 балів.

Завдання.1.

 У відкритому морі знаходяться кораблі,їх рух заданий рівняннями. Визначити, які з них рухаються паралельним курсом,пояснити відповідь.

1. у = 6х+5/3
2. у = 10-2х
3. у = 7х+4/7
4. у = 2х+0,25
5. у= -2х -5
6. у = 9 + 7x

Завдання 2. Графіком функції у = х  є…(бісектриса 1 та 3 півплощини)

Графіком функції у = -х  є…(бісектриса 2 та 4 півплощини)

1) Що буде графіком функції у = |х| ?

2) Що буде графіком функції у = |х| + b ?

3) Що буде графіком функції у = - |х|  ?

4) Що буде графіком функції у = - |х|+ b ?

Завдання 3. Визначити  рівняння кожної прямої за її зображенням:

1. у = 0,7х - 2
2. у = -1,5х - 5
3. у = 3 - 0,8х
4. у = 2х
5. у= 2х +2
6. у=-0,5x

Рефлексія.

 Закінчите, будь ласка, речення:

1)   Сьогодні на занятті я засвоїв (зрозумів, зумів ...);

2)   Мені сподобалося... ;

3)  Я вважаю, що завдання, які ми сьогодні з великим інтересом вирішували, допоможуть ... ;

4) Я вважаю, що час, проведений на цьому уроці ...

Додаток

Питання для гри «Скарби гномів».  Правильні відповіді виділені.

1.               Через  яку з точок проходить графік функції     у = 3х+2

 1) А(3;5)       2) В(8;13)       3) D(4;14)     4) С(2;7)

2.               Графік функції  у = 2х + 10 перетинає вісь Ох у точці з координатами 

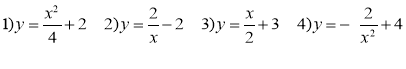  1) (0;0)       2) (0;10)            3)  (-5;0)        4) (-5;10)

3.               Яка з функцій є лінійною
4.               Графік функції   у = -х+5 перетинає вісь Оу в точці з координатами

   1)  (0;5)         2)    (0;0)     3)  (1;1)         4)    (5;0)

5.               Яка з функцій є прямою   пропорційністю:  1) у = 2х+3; 2) у = 3х;

3) у = х²   4) у = 3.

6.               Графік якої з функцій проходить через точку А(-1;2):  1) у = 2х    2) у = 5х + 3 

         3) у = 3х – 2   4) у = 2х + 4

7.               Графік якої з функцій проходить через точку А(-3;1)   1) у = 2х   2) у = 5х + 3

        3) у = 3х – 2  4) у = х + 4

8.               Сформулювати означення лінійної функції
9.               Яку  функцію називають прямою пропорційністю
10.          Яка з функцій зростаюча?   1) у = -2,4х;  2) у = 0,24х;  3) у = -7х;    4) у = - 0,4х
11.          Яка з функцій спадна?   1) у  = 2,4х;  2) у  = 0,24х;  3) у  = - 0,4х;    4) у  =  27х
12.          Який з графіків зайвий…
13.          Яка з функцій зайва? 1) у = 2х – 3;  2) у = 5х+4;  3) у = 3х – 2;  4) у = х² +5
14.          Яка лінія є графіком лінійної функції   1)крива; 2) пряма; 3) коло;  4) ламана.
15.          Якщо k > 0,    то кут між графіком та віссю Ох:  1) тупий;  2) прямий; 

3) гострий;  4) розгорнутий

16.          Якщо k<0, то функція…1) не змінюється;  2)зростає;   3)спадає;  4)  стабільна
17.          Координати скількох точок достатньо знати, щоб побудувати графік лінійної    функції?  1) трьох;      2) двох;   3) однієї;               4) п’яти.
18.          У  лінійної функції k < 0. Функція…?  1) інша відповідь; 2) зростає;

          3) стала;  4) спадає.

19.          Які значення х   НЕ входять до області визначення функції                       

          1) 0 і 3;  2) -2;   3) 0 і 2;     4) 2 і 3

20.          Знайти значення функції   при х = - 0,2

         1) 5;  2) -5;   3) 7;     4) -2

21.          Який з графіків не перетинає вісь Ох?1) у = х; 2) у = -3;  3) у = - х;  4) у=2х +3
22.          При якому значенні k  графік функції  у=kх +7 проходить через точку С(2;-1)

         1)  -4;         2) 4;           3)  -3;        4) 3

23.          Що таке графік функції?
24.          Як можна задавати функцію?