Позакласний захід "Математика і гармонія"

МАТЕМАТИКА І ГАРМОНІЯ

Усний журнал для учнів 9 класу

Мета: підвищити інтелектуальний рівень учнів; показати, що для математики характерні непохитність висновків, краса ідей, до­сконалість мови; довести, що математика — об'єкт гармонії.

Обладнання: комп'ютер, мультимедійний проектор.

Підготовка заходу. Усі учні класу об'єднані в три коман­ди. Кожна команда готує завдання:

• Вислови про математику;
• Розповідь про жінку – математика.

Математика — об'єкт гармонії; Логіка — мистецтво міркування; Математичне подання реальності; Чи можна виміряти красу.

До кожної сторінки журналу перед­бачено завдання, розв'язуючи які команди набирають бали, тобто беруть участь у конкурсі. Усім командам пропонують одне й те саме завдання. Якщо не зауважено окремо, то команда, яка першою пра­вильно виконає завдання, отримує 3 бали, другою — 2 бали тощо, третьою – 1 бал. Найбільша кількість балів забезпечує перемогу.

ХІД ЗАХОДУ

На екран проектують висловлювання ви­датних учених про математику, які відповіда­ють темі журналу.

Учитель. Математика володіє здатністю відображати і моделювати будь-які процеси на­вколишнього світу. Математика — це поєднання абстрактності, логічності, методів, ідей, матема­тичної мови в одне органічне ціле. Внутрішня впорядкованість математики сприяє розвитку фундаментальних ідей. Закони математики (си­метрія, пропорція, періодичність) відображають закони гармонії в природі. Непохитність ви­сновків, краса ідей, досконалість мови, корис­ність — складові краси математики.

Коли читаєш слова І. Г. Зенкевича «Най­кращі доведення в математиці є короткими й точними, наче епіграми...», на думку спадає теорема Піфагора, теореми косинусів і синусів, бо вони є носіями краси і досконалості.

Сьогодні ми поговоримо про красу самої математики та красу, яку вона створює.

Перша сторінка. Математика — об'єкт гармонії

Існує легенда, ідо одного разу священик про­вів проповідь без єдиного слова. Він просто про­стягнув своїм прихожанам квітку. Якщо уваж­но роздивитись квітку, то можна знайти єдність і порядок у всьому: формі, кольору, розташу­ванні та розміру листочків і пелюсток. Порядок і єдність — це гармонія, що визначає красу.

Перед вами «листочки», на яких написано такі слова:

абстрактність, логіка, ідеї, методи, модель, рівняння, нерівність, функція, алгоритм, анало­гія, зв'язок, додавання, порядок, віднімання, інтеграл, злагодженість, послідовність, відпо­відність, стрункість, математична мова тощо. Ті листочки, на яких написано слова, що мають від­ношення до математики, прикріпіть до дерева.

(Макет дерева виготовлено з паперу, лис­точки заготовлено з булавочками. Учні визна­чають, які слова мають відношення до матема­тики, і прикріплюють їх до «дерева».)

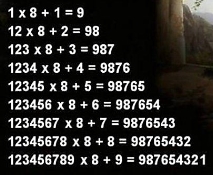— Подивіться, як багато листочків виросло на дереві. Це зрозуміло, адже математика — складний і тонко побудований організм, і всі його компоненти не можуть існувати один без одного.

Подивимось на наступні слайди: і ми переконаємось у цьому.

Отже, математика — це об'єкт гармонії, бо тут існує поєднання різних компонентів, ство­рених уявою людини, в єдине ціле.

Завдання 1. Пропоную капітанам команд на­вести заздалегідь заготовлені висловлювання, які дають відповідь на запитання «Що таке математика? ».

 За кожне висловлювання коман­да отримує 1 бал.

(Капітани команд по черзі наводять заго­товлені висловлювання.)

Завдання 2. Не відриваючи олівця від паперу, побудуйте малюнок.

За правильно виконане завдання коман­да отримує 2 бал.

Завдання 3.

Не відриваючи олівця від паперу, побудуйте чотириланкову ламану, яка проходить через 9 точок: вершини, середини сторін і центр квадрата.

     За правильно виконане завдання коман­да отримує 2 бал.

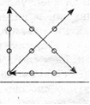
Краса розв'язку полягає в його несподі­ваності: ламана перетинає себе і виходить за межі квадрата. Вихід за межі квадрата зда­ється безглуздим, проте саме ця ідея дозволяє знайти розв'язок. Отже, математичним мірку­ванням красу додають сміливі ідеї, наочність, несподіваність.

Друга сторінка. Логіка — мистецтво міркування

Логіка (від давньогрецького ) — розділ філософії, «наука про правильне мислення», «мистецтво міркування», «мова», «міркування», «думка») — наука про форми, методи і закони інтелектуальної пізнавальної діяльності. Логіку також визначають як науку про форми і закони правильного мислення. Оскільки мислення оформлюється мовою у ви­гляді міркування, окремими випадками якого є доведення і спростування, логіку іноді визна­чають як науку про способи міркування або науку про способи доведень і спростувань.

Математична логіка — розділ математики, що вивчає доведення і питання основ матема­тики.

Спершу вгадати, а потім довести — прин­цип, за яким було зроблено більшість матема­тичних відкриттів.

Під час розв'язування задач і доведення те­орем курсу шкільної геометрії найчастіше за­стосовують теорему ГІіфагора. Причинами такої популярності є її простота, краса, значення.

Теорема Піфагора чудова тим, що сама по собі зовсім не очевидна. Наприклад, властивості рівнобедреного трикутника можна побачити без­посередньо на рисунку. Проте скільки не дивись на прямокутний трикутник, ніяк не побачиш, що між його сторонами є таке просте співвід­ношення: квадрат гіпотенузи дорівнює сумі квадратів катетів. Час не має вітливу на красу математичної істини. Одного разу доведена те­орема вже ніколи не може бути неправильною. Така теорема, як теорема ГІіфагора, прекрасна сьогодні, як і того дня, коли її було відкрито.

Завдання 5. Скориставшись рисунком (слайд), складіть і розв'яжіть задачу на застосування теореми Піфагора.

За правильно виконане завдання коман­да отримує 2 бал.

Завдання 6.

На аркуші записані кольори. Потрібно прочитати слова за кольорами.

За правильно прочитане слово 1  бал.

Завдання 7

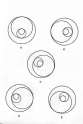
Яка  фігура зайва?                                                                                    За правильну відповідь 1 бал   

Третя сторінка.
Математичне подання реальності.

Математичне подання реальності — це ма­тематична модель. Усі природничі і суспільні науки, які використовують математичний  апарат, по суті займаються математичним моделюванням : замінюють реальний об'єкт його мате­матичною моделлю і потім вивчають останню.

Математична модель — це формула, рівняння, нерівність, система рівнянь або нерівностей, рисунок тощо. Тобто математична модель — це опис реального світу (процесу) мовою математичних понять.

Цінність математичного моделювання полягає в тому, що одна й та сама модель може описувати різні процеси людського життя. На слайді показано, як люди різних професій сприймають запис.

Завдання 8 . Скласти математичну модель до задачі.

 За правильну відповідь 2 бали.

Четверта сторінка.
Чи можна виміряти красу?

З курсу математики 6-го класу ми знаємо, що пропорція — це рівність двох відношень. Але це слово має й інше значення. Пропорція — це співвідношення частин цілого між собою. Пропорція відіграє основну роль у симетричних конструкціях, зокрема архітектурних спорудах, кристалах мінералів тощо. Існує пропорція, використання якої робить неперевершеними твори в різних галузях мистецтва: музиці, поезії, архітектурі тощо. Це ділення цілого на дві нерівні частини, за якого більша частина так відноситься до цілого, як менша частина — до більшої. Такий поділ називають золотим перерізом. Це дивовижне співвідношення; де воно зустрічається — там панує краса.

Золотий переріз — це універсальний принцип гармонії, найвищий прояв структурної і функціональної досконалості відношення цілого і його частин у мистецтві, науці, техніці, природі.

Золотий переріз використовують архітектори, художники, дизайнери для створення своїх шедеврів.

Завдання 9. Нехай довжина відрізка с, зображеного на слайді 14, дорівнює 1. Знайдіть довжини відрізків а і Ь (округліть до тисячних) і відношення а: Ь і Ь:а.

(Відповідь, а ~ 0,382, Ь = 0,618, а:Ь = 0,618, Ь:а = 1,618.)

Число ф = 1,618 називають золотим числом. Отже, і що таке краса? — Міф чи закономірне явище, описане математично? Чому число ф = 1,618 називають золотим?

Відношення двох величин, яке дорівнює 1,618, нерідко можна зустріти в живій природі: павук створює свою павутину у формі логарифмічної спіралі, яка містить точки золотого перерізу, у багатьох метеликів співвідношення розмірів грудної та черевної частини тіла відповідає золотій пропорції, бабка створена за законами золотої пропорції: відношення довжини хвоста до довжини корпусу дорівнює відношенню загальної довжини до довжини хвоста, насіння соняшника і багатьох інших рослин розташоване у формі логарифмічної спіралі. Більш того, навіть у будові людського тіла присутнє золоте число: талія ділить досконале людське тіло у відношенні золотого перерізу, також зіставляючи довжини фаланг пальців і кисті руки, відстані між окремими частинами людського обличчя, можна знайти золоті співвідношення.

Можливо, красу можна виміряти числом  1,618?

Основою краси багатьох форм, створених природою і людиною, є симетрія. Симетрія (від грец. міряти разом, відповідність) — властивість об'єкта відтворювати себе за певних трансформацій, які називають операціями симетрії. Симетрія — передусім геометричне поняття, однак його також застосовують до негеометричних об'єктів у математиці, фізиці, хімії, біології, в інших галузях людської діяльності: філософії, естетиці, соціології, мистецтві тощо.

Симетрія — засіб створення художнього образу, гармонії. Із симетрією людина зустрічається повсякденно в природі і техніці, вона проходить через усю багатовікову історію людської творчості, її широко використовують архітектори, живописці, скульптори, художники- конструктори. Симетрія, яку людина розкрила і осмислила у творіннях природи, ставала для неї поступово своєрідною нормою прекрасного, люди починали свідомо використовувати симетрію як засіб гармонійної організації форми. Давні греки вважали, що Всесвіт симетричний просто тому, що симетрія прекрасна. Ідея симетрії часто була відправним пунктом у гіпотезах і теоріях учених минулих століть, які вірили в математичну гармонію світобудови.

Завдання 10

На рисунку зображено візерунок для вишиванки. Відтворіть візерунок повністю,якщо він має чотири осі симетрії.

За правильно виконане завдання 2 бали.

Учитель. Людей завжди цікавило питання, чи підпорядковуються такі речі, як краса і гармонія, математичним формулам. Звісно, всі закони краси не можна помістити в декілька формул. Але я сподіваюся, що, гортаючи сторінки нашого журналу, ви відкрили для себе деякі складові прекрасного. Дякую за роботу.

Журі підбиває підсумки конкурсу

ЛІТЕРАТУРА

1. Глейзер Г. И. История математики в школо. — М. : Просвещение, 1982.
2. Баран О. І. Математичні мініатюри. — X. : Ви­давнича група «Основа», 2003.
3. Вірченко Н. О. Про красу математики // Мате­матика. — 2005. — № 11. — С. 3-4.
4. Зепкевич И. Г. Зстетика урока математики. — М. : Просвещение, 1981.

5. ІПмигевский Н. В. Формула совершенства // Країна знань. — 2006. — № 6. — С. 9-12.

.